Open- vs. closed-path eddy covariance measurements of the net ecosystem carbon dioxide and water vapour exchange: a long-term perspective

Abstract

The differential design, deployment and data post-processing of open- (OP) and closed-path (CP) eddy covariance systems is a potential source of bias for ongoing global flux synthesis activities. Here we use a unique six year data set of concurrent CP and OP carbon dioxide (CO₂) and water vapour (H₂O) eddy covariance flux measurements above a temperate mountain grassland in Austria to explore the consequences of these differences on a long-term basis. The theoretically based transfer function approach was able to account and correct for the differences in low-pass filtering between the two systems. Corrected CO₂ and H₂O fluxes exhibited excellent 1:1 correspondence, but the CP system tended to underestimate OP H₂O fluxes during conditions of high air temperature, wind speed and global radiation, large sun angles and low relative humidity. Corrections for self-heating of the OP infra-red gas analyser had a very small effect on these relationships. Energy balance closure was slightly more favourable for the OP system. No significant differences were found for the random flux uncertainty of both systems. A larger fraction of OP data had to be excluded because of obstructions of the infra-red path by water and snow. This, however, did not translate into a correspondingly larger fraction of accepted CP flux values, because of a larger percentage of CP flux data failing on the stationarity test. Integrated over the annual cycle, the CP system yielded on average a more positive net ecosystem CO₂ exchange (25 vs. 0 gC m⁻² y⁻¹) and a lower evapotranspiration (465 vs. 549 mm y⁻¹) as compared to the OP system.

1. Introduction

The Earth’s climate has been changing continuously (Ruddiman, 2007), but during recent years reports on extreme climatic states and accelerating rates of change have increased substantially and according to the IPCC (2007) it is very likely that anthropogenic increases in greenhouse gas concentrations are responsible for these changes, in particular global warming. Understanding biotic feedback from/to these changes requires quantification of the rates at which the Earth’s ecosystems exchange mass and energy with the atmosphere and how these exchange process respond to changes in climate forcing and land-use change (Heimann and Reichstein, 2007).

The FLUXNET project (Baldocchi et al., 2001; Baldocchi, 2008), which integrates regional and national flux monitoring projects worldwide, has been initiated for quantifying carbon dioxide (CO₂), water vapour (H₂O) and energy fluxes of terrestrial ecosystems. To this end, the preferred technique is the eddy covariance (EC) method (Aubinet et al., 2000; Baldocchi, 2003), which allows direct measurement of the net ecosystem-atmosphere flux on spatial and temporal scales of km² and hours to decades, respectively, by deriving the covariance between the vertical wind speed and the mixing ratio of the scalar of interest.

Infra-red gas analysers (IRGA) are most commonly used for measuring CO₂ and H₂O concentrations and researchers have to choose between a so-called open-path (OP) and closed-path (CP) IRGA design. The former quantify scalar concentrations in situ, close to the point where the vertical wind speed (usually by means of a sonic anemometer) is measured. The latter are situated at some distance from this point (typically in a weather-proof enclosure at the base of the tower) and quantify scalar concentrations of air sucked down through a tube from an intake close to the anemometer. There are pros and cons for each of the two systems: OP system typically consume less power as compared to CP systems which require a pump (and possibly tube heating) and are thus better suited for remote locations without line power (but see Goulden et al., 2006). OP systems usually also require less maintenance as opposed to CP systems (but see Serrano-Ortiz et al., 2008), where filters in the air stream require regular replacement and pump wear needs to be closely monitored (Aubinet et al., 2000; Mauder et al., 2008). On the other hand, data from OP IRGAs become erroneous when the turbidity of the window through which the infra-red beams pass exceeds a given threshold, usually caused by accruing water (precipitation, dew) and/or dirt. Under conditions where this happens frequently, a comparably large fraction of data gaps needs to be filled, which in turn increases the uncertainty of the annual flux estimates (Moffat et al., 2007). Whether an OP or CP EC system is used also has a prominent influence on the post-processing of data, in particular with regard to corrections which need to be applied to the raw covariances: Similar frequency response and sensor geometry provided (which for currently available commercial instruments is generally the case) and given similar deployment of the OP IRGA and CP intake, corrections for low-pass filtering are of similar magnitude, except for the tube-related dampening and phase shift of concentration fluctuations (Massman, 2000), which typically constitute the major terms in the frequency response corrections of CP systems and need not be applied with OP systems. On the contrary, the correction for air density fluctuations related to concurrent fluctuations in air heat and water vapour content (Webb et al., 1980) is quantitatively much more significant for OP systems, because with CP systems temperature fluctuations have been shown to quickly dampen out as air travels through the tube (Aubinet et al., 2000), leaving only water vapour fluctuations to be corrected for (Massman, 2004). In addition, it was recently discovered (Burba et al., 2006) that OP EC systems also have to account for density fluctuations caused by the self-heating of OP IRGAs.

These differences in data post-processing are a potential source of systematic bias and have attracted the interest of the pioneers of modern EC already in the 1990ies (see for example Leuning and Moncrieff, 1990; Leuning and King, 1991; Suyker and Verma, 1992). Overall, these early comparisons of OP and CP systems showed that careful application of all required corrections provided, little systematic bias exists, which has been corroborated by later comparisons of this kind (e.g. Yasuda and Watanabe, 2001; Ocheltree and Loescher, 2007; Wohlfahrt et al., 2008b), while yet others found large differences (e.g. Anthoni et al., 2002; Hirata et al., 2007; Ono et al., 2007). However, most of the above-cited studies (except for Hirata et al., 2007) were confined to relatively short time periods and thus the question arises as to whether the findings from these short-term studies are valid for today’s long-term flux measurement programs, where the seasonal, inter-annual and decadal variability of CO₂ and H₂O fluxes and inter-comparisons between ecosystems around the globe are thought for (Baldocchi et al., 2001; Baldocchi, 2008). Temporal bias may arise for example from the fact that during the early years of European flux measurement networks CP IRGAs (in fact one particular model; Aubinet et al., 2000) were used more frequently, while during recent years OP systems have gained increasing popularity. Spatial bias may arise in case a preference for CP or OP systems exists with regard to certain regional/national networks, climates and/or biomes.

The aim of the present study is to assess the long-term bias between OP and CP EC flux measurements by analysing a unique data set from a temperate mountain grassland in Austria, where concurrent OP and CP flux measurements have been performed since 2001. Using this data set we will analyse differences between OP and CP systems with regard to the following issues: i) our ability to account for low-pass filtering, ii) a paired (that is for all pairs of data where concurrent CP and OP flux estimates are available) comparison of fluxes and the relation of the residuals to environmental conditions, iii) energy balance closure, iv) random flux uncertainty, v) gap statistics, and vi) gap-filled annual flux estimates.

2. Material and Methods

2.1 Site description

The study site is located at a meadow in the vicinity of the village Neustift (47°07′N, 11° 19′E) in the Stubai Valley (Austria) at an elevation of 970 m a s l. in the middle of the flat valley bottom. The fetch is homogenous up to 300 m to the east and 900 m to the west of the instrument tower, the dominant day and night time wind directions, respectively. The average annual temperature is 6.5 °C, average annual precipitation amounts to 852 mm. Further details on soil and vegetation characteristics may be found in Wohlfahrt et al. (2008a).

2.2 Eddy covariance

Within this paper EC data from the period 2001-2006 are presented (Hammerle et al., 2008; Wohlfahrt et al., 2008a). The net ecosystem CO₂ and H₂O exchange was measured using the eddy covariance method (Aubinet et al., 2000; Baldocchi, 2003). The three wind components and the speed of sound were measured by a three-dimensional sonic anemometer (R3IA, Gill Instruments, Lymington, UK), CO₂ and H₂O mole densities/fractions by an OP (Li-7500, Li-Cor, Lincoln, NE, USA) and a CP (Li-6262, Li-Cor, Lincoln, NE, USA) IRGA. In the CP system air was sucked from the inlet, displaced 0.1 m laterally and 0.1 m below the centre of the sensor volume of the sonic anemometer mounted at 3 m above ground, through a 4 m Teflon tube of 0.004 m inner diameter through a filter (Acro 50, Gelman, Ann Arbor, MI, USA) to the CP IRGA at a flow rate of 9 l min⁻¹ (N035ANE, KNF Neuberger, Freiburg, Germany). The CP IRGA was operated in the absolute mode, flushing the reference cell with dry N₂ from a gas cylinder at 0.1 l min⁻¹. CP CO₂ and H₂O concentrations were corrected online for the effect of water vapour dilution (Ibrom et al., 2007a). The OP IRGA was displaced 0.3 m laterally and 0.2 m below the centre of the sensor volume of the sonic anemometer and was tilted at an angle of 45° towards North. Both the CP and OP IRGA were arranged approximately at a right angle to the main daytime and nighttime wind direction thereby minimizing longitudinal sensor separation to the sonic anemometer. Raw voltage signals of the CO₂ and H₂O mole fractions/densities from both IRGAs were input at 10 Hz by the analogue input of the sonic, where they were synchronized with the sonic signals, which were output at 20 Hz. All raw data were saved to a hard disc of a personal computer for post-processing using the EdiSol software (University of Edinburgh).

Half-hourly mean eddy fluxes were calculated as the covariance between the turbulent departures from the mean of the vertical wind speed and the CO₂ and H₂O mixing ratios using the post-processing software EdiRe (University of Edinburgh). Means and turbulent departures there from were calculated by Reynolds (block) averaging. The tube-induced time delay of the CO₂ (0.7 s) and H₂O (0.9 s) signals was determined by optimizing the correlation coefficient with the vertical wind velocity (McMillen, 1988) within a given time window. A fixed lag of 0.3 s was imposed on the OP data through the IRGA software and removed. A three-axis co-ordinate rotation was performed aligning the co-ordinate system’s vector basis with the mean wind streamlines (Kaimal and Finnigan, 1994). Frequency response corrections were applied to raw eddy fluxes accounting for high-pass (block averaging) and low-pass (lateral sensor separation, dynamic frequency response, scalar and vector path averaging, frequency response mismatch and in the case of the CP IRGA the attenuation of concentration fluctuations down the sampling tube) filtering following Moore (1986), Massman (1991) and Aubinet et al. (2000). To this end, a site-specific model cospectrum, described in Wohlfahrt et al. (2005), was employed. Finally density corrections were applied to OP fluxes based on Webb et al. (1980) – for the CP fluxes this was not necessary as temperature fluctuations were assumed to have been dampened out by the time when air arrives in the IRGA (Aubinet et al., 2000) and water vapour (dilution) effects were accounted for online in the CP IRGA (Ibrom et al., 2007a). In addition, OP fluxes were corrected for the effect of self-heating of the IRGA following Burba et al. (2006) – the applicability of this correction will be assessed in the following.

The net flux of CO₂ and H₂O was calculated as the sum of the corrected vertical eddy term and the storage fluxes, the latter being estimated from the time-rate-of-change of the CO₂ and H₂O density at the reference height, which in a previous comparison with a profiling system was found to be sufficiently accurate. Negative fluxes represent transport from the atmosphere towards the surface, positive ones the reverse.

2.3 Ancillary data

Supporting meteorological measurements of relevance to this study included total and diffuse photosynthetically active radiation (PAR) (BF3H, Delta-T, Cambridge, UK), global and net radiation (CNR-1, Kipp & Zonen, Delft, Netherlands), air temperature (T_air) and humidity (RH) at 2 m height and soil temperature (T_soil) at 0.05 m depth, measured by the means of a combined temperature/humidity sensor (RFT-2, UMS, Munich, Germany) and a thermocouple (TCAV, Campbell Scientific, Logan, UT, USA), respectively, soil heat flux (G) measured by the means of heat flux plates (3 replicates at 0.05 m depth; HFP01, Hukseflux, Delft, The Netherlands) corrected for the change in heat storage above that depth using the calorimetric method (Sauer and Horton, 2005), volumetric soil water content (ML2x, Delta-T Devices, Cambridge, UK) and precipitation (52202, R. M. Young, Traverse City, MI, USA).

2.4 Quality control, gap-filling, uncertainty analysis, statistics

Half-hourly flux data were quality controlled by removal of time periods with (1) the CO₂ or H₂O signal outside a specific range, (2) the coefficient of variation for CO₂ or H₂O concentration and, in the case of the CP IRGA, internal pressure outside a specific range, (3) the third rotation angle exceeding ± 10° (McMillen, 1988), (4) the stationarity test for the CO₂ and H₂O flux exceeding 60% (Foken and Wichura, 1996), (5) the deviation of the integral similarity characteristics larger than 60% (Foken and Wichura, 1996), and (6) the maximum of the footprint function (Hsieh et al., 2000) outside the boundaries of the meadow (cf. Novick et al., 2004). In order to avoid the potential underestimation of nighttime ecosystem respiration during calm and stable conditions (Gu et al., 2005), nighttime NEE data were excluded when friction velocity (u_*) was below 0.2 m s⁻¹ (Wohlfahrt et al., 2005) when calculating annual flux estimates.

In order to derive continuous flux time series, required for calculating annual NEE and evapotranspiration, the following gap filling procedure was employed: Gaps less than two hours were filled by linear interpolation. Larger gaps were filled by means of the look-up table approach (using a combined PAR and T_air matrix) or, if not possible, by the mean diurnal variation method (Falge et al., 2001a,b).

The random uncertainty of the half-hourly CO₂ and H₂O flux measurements was determined based on measurements under similar environmental conditions during adjacent days as proposed by Hollinger and Richardson (2005).

3. Results

Low-pass filtering

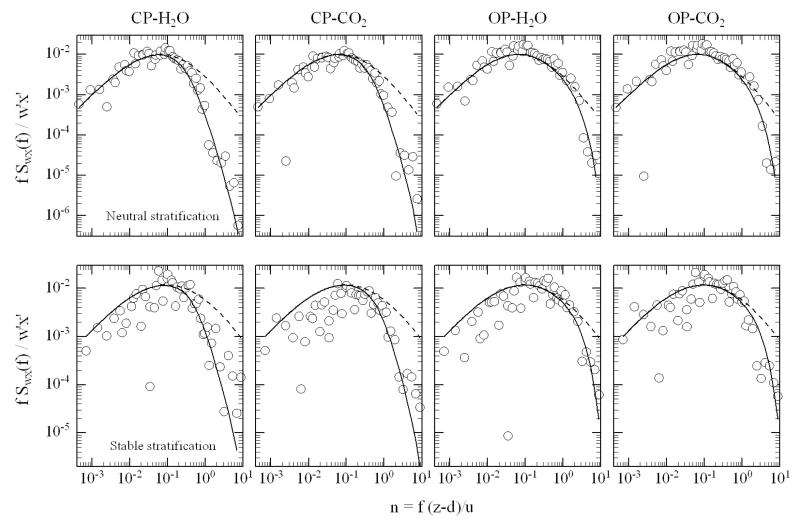
A cospectral analysis was conducted in order to assess differences in low-pass filtering between the OP and CP system and to test the ability of the frequency response corrections to adequately account for this flux loss. To this end, Fig. 1 shows, separately for near-neutral and stable conditions, measured cospectra, model cospectra (for details see Wohlfahrt et al., 2005) and model cospectra attenuated by a series of transfer functions which simulate the effect of low-pass filtering. Differences in low-pass filtering between the OP and CP system are clearly evident: for the windy conditions shown in Fig. 1 the attenuation of high frequency flux contributions commenced at lower frequencies and was more severe for the CP as compared to the OP system (Fig. 1). The attenuated model cospectra generally overlapped with the measured cospectra (r² 0.50-0.86) indicating that the applied frequency response corrections were able to account for the observed flux loss at high frequencies (Fig. 1). Averaged over the six study years the frequency response correction factors (including high-pass filtering) amounted to 1.12 for the OP (CO₂ and H₂O) and 1.12 and 1.15 for the CO₂ and H₂O CP system, respectively (2.3 % of which are due to high-pass filtering).

Figure 1.

Comparison between measured cospectra (symbols), site-specific model cospectra (solid lines; see Wohlfahrt et al., 2005) and model cospectra attenuated with appropriate transfer functions to account for high frequency losses of CP and OP systems. Upper and lower panels refer to near-neutral (13.07.2003 11:30-12:00; average wind speed = 3.3 m s⁻¹) and stable (19.07.2003 20:00-20:30; average wind speed = 2.1 m s⁻¹) conditions, respectively.

Paired flux comparison

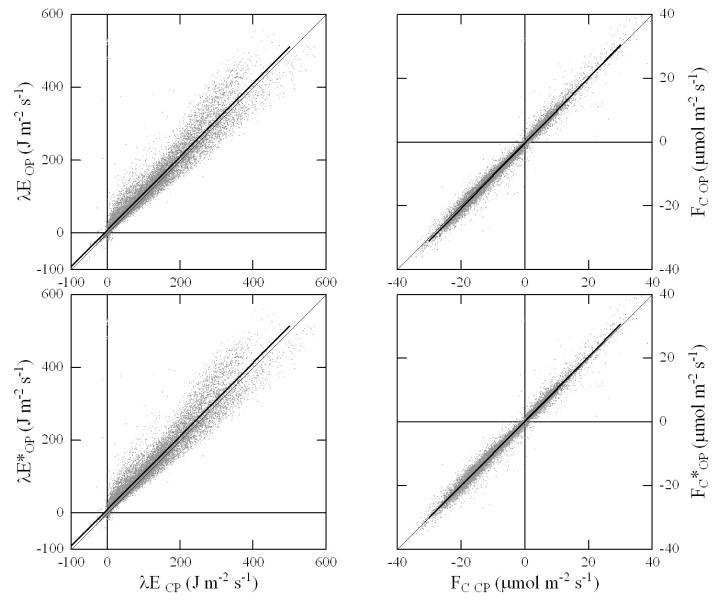
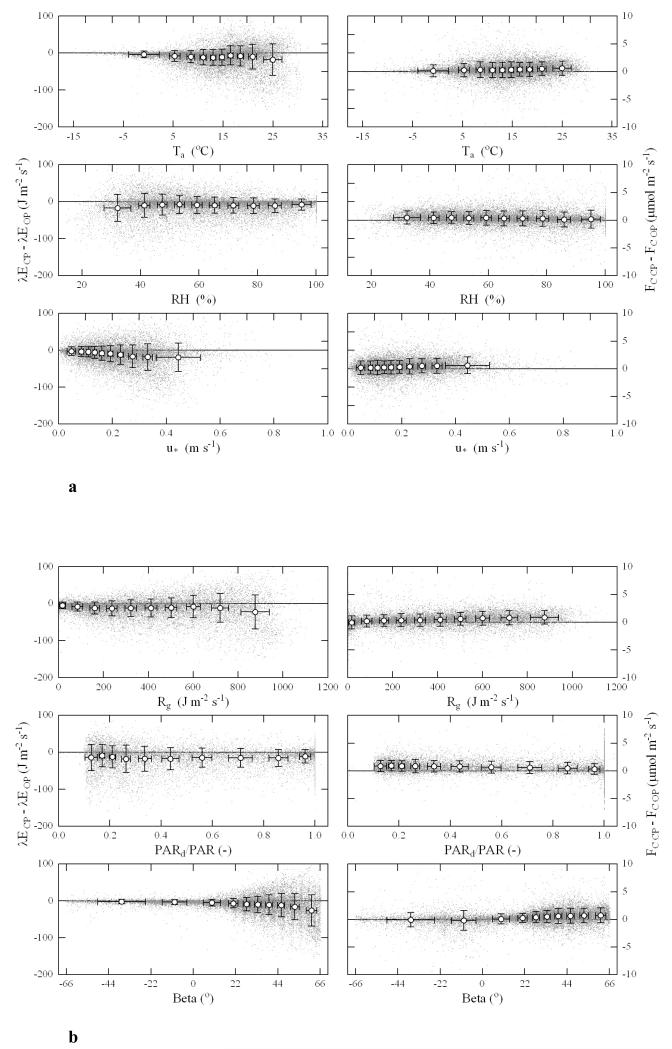
Figure 2 shows a comparison of all pairs of data when concurrent valid OP and CP data were available – for the OP flux data both without (upper panels) and with (lower panels) the correction for IRGA self-heating (Burba et al., 2006) applied. Not correcting for OP IRGA self-heating, linear regressions through these data explained 95 and 99 % of the variability in latent heat and CO₂ fluxes, respectively, and yielded slopes close to unity (λE: 1.004 and F_C: 1.025), positive y-intercepts of less than a few percent of maximum flux values (λE: 9.3 J m⁻² s⁻¹ and F_C: 0.22 μmol m⁻² s⁻¹) and mean absolute errors (MAE) of 16.7 J m⁻² s⁻¹ and 0.88 μmol m⁻² s⁻¹. A paired T-test shows that CP and OP averages were statistically significantly different (p < 0.001) for both CO₂ and latent heat fluxes. Applying the correction for IRGA self-heating to the OP data changed regression statistics only marginally – slightly for the worse for latent heat fluxes (λE_{_OP} = 1.007 λE_{_CP} + 9.8, r² = 0.95, MAE = 17.1), while a small improvement was observed for CO₂ fluxes (F_{C_OP} = 1.012 F_{C_CP} + 0.33, r² = 0.99, MAE = 0.86) – even when data were restricted to low air temperatures (< 0°C), when the self-heating effect is expected to be largest (data not shown). Because of the small nature of these changes we did not apply the self-heating correction to the OP data in the following, as will be discussed below. Figures 3a-b show the residuals of the paired comparison as a function of several environmental driving forces which may affect the performance of the two EC systems. There it can be seen that the difference in CO₂ flux between the CP and OP system was largely independent of the various environmental parameters, while the CP system tended to yield lower latent heat fluxes than the OP system during conditions of high air temperature, wind speed and global radiation, large sun angles (which might interfere with the OP concentration measurement) and low relative humidity, while no clear pattern could be detected for the fraction of diffuse PAR (Figs. 3a-b).

Figure 2.

Paired comparison between OP (y-axis) and CP (x-axis) latent heat (left panels) and CO₂ (right panels) fluxes. OP fluxes marked with a star have been corrected for the effect of OP IRGA self-heating according to Burba et al. (2006). Symbols represent half-hourly fluxes, thin solid lines the 1:1 correspondence, and thick solid lines linear regressions (refer to text for regression statistics).

Figure 3.

Residuals (differences between CP and OP fluxes) of latent heat (left panels) and CO₂ (right panels) fluxes as a function of a) air temperature (T_a), relative humidity (RH) and friction velocity (u_*), and b) global radiation (R_g), fraction of diffuse photosynthetically active radiation (PAR_d/PAR) and the sun’s elevation (β). Grey symbols refer to half-hourly averages, open symbols with error bars to bin-averages ± one standard deviation.

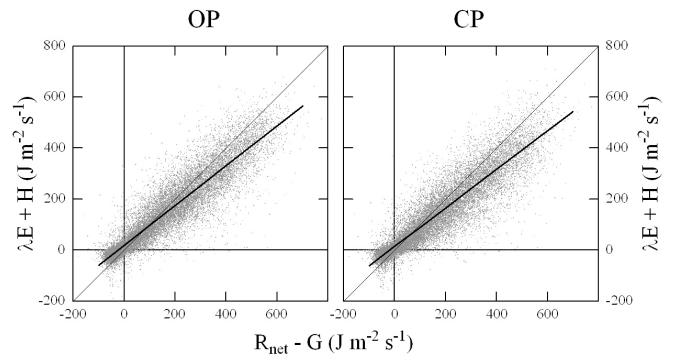
Energy balance closure

The ability of the two EC systems to close the energy balance was assessed by comparing the available energy, that is the net radiation minus the soil heat flux, with the sum of the latent and sensible heat, as shown in Fig. 4. As may be deduced already from Fig. 2, differences in energy balance closure between the CP (H + λE = 0.76 (R_net – G) + 14.24, r² = 0.84) and the OP (H + λE = 0.78 (R_net – G) + 19.87, r² = 0.85) system were small for the paired data, with a slightly more favourable closure for the OP system. This difference became more prominent if using for each system all valid data (CP: H + λE = 0.73 (R_net − G) + 10.10, r² = 0.82; OP: H + λE = 0.78 (R_net − G) + 16.80, r² = 0.88).

Figure 4.

Energy balance closure for the OP (left) and CP (right) system. Plotted are the available energy (net radiation minus soil heat flux) on the x-axis and the sum of sensible and latent heat flux on the y-axis. Symbols represent half-hourly fluxes, thin solid lines the 1:1 correspondence, and thick solid lines linear regressions (refer to text for regression statistics).

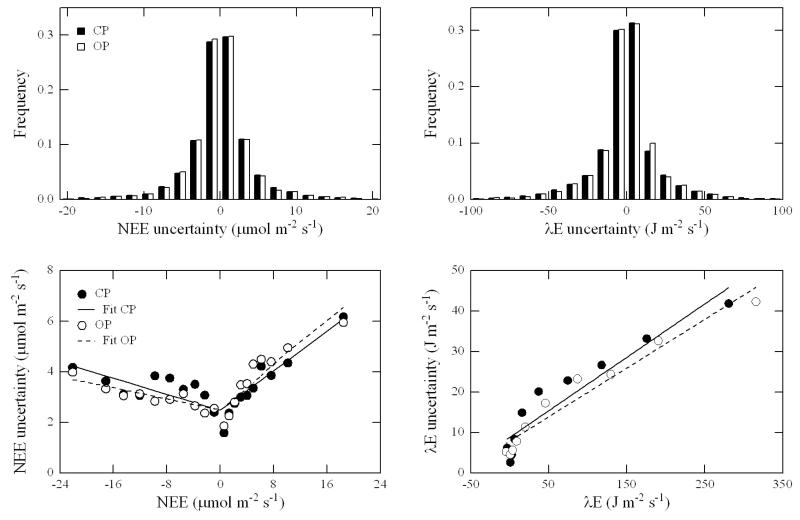
Random flux uncertainty

The probability density distribution of the random flux uncertainty followed a double-exponential rather than a normal distribution for both CO₂ and latent heat fluxes and differences between the OP and CP system were generally minimal (Fig. 5). Double-linear and linear relationships with the flux magnitude explained 78-95 % of the variability of the random CO₂ and latent heat flux uncertainty, respectively. Again, differences between the OP and CP system were small with slightly higher random latent heat flux uncertainties for the CP system and larger daytime (negative NEE) random CO₂ flux uncertainties of the CP and larger nighttime (positive NEE) random uncertainties for the OP system (Fig. 5).

Figure 5.

Analysis of random flux uncertainty according to Richardson and Hollinger (2005). Panels on the left and right show CO₂ and latent heat flux random uncertainties, respectively. Upper panels show the probability density distribution of random flux uncertainties, lower panels the best parameterisation of random flux uncertainties. For the random CO₂ flux uncertainty a double-linear relationship with the flux magnitude was used to describe variability in uncertainty (CP: y = 0.19× + 2.48 and y = −0.08× + 2.48, r² = 0.78; OP: y = 0.20× + 2.50 and y = −0.05× + 2.50, r² = 0.86), while for the random latent heat flux uncertainty a single linear relationship was used (CP: y = 0.13× + 8.83, r² = 0.89; OP: y = 0.12 + 7.90, r² = 0.95). Closed bars/symbols and solid lines refer to the CP system, open bars/symbols and broken lines to the OP system. Symbols represent bin-averages with equal numbers of observations.

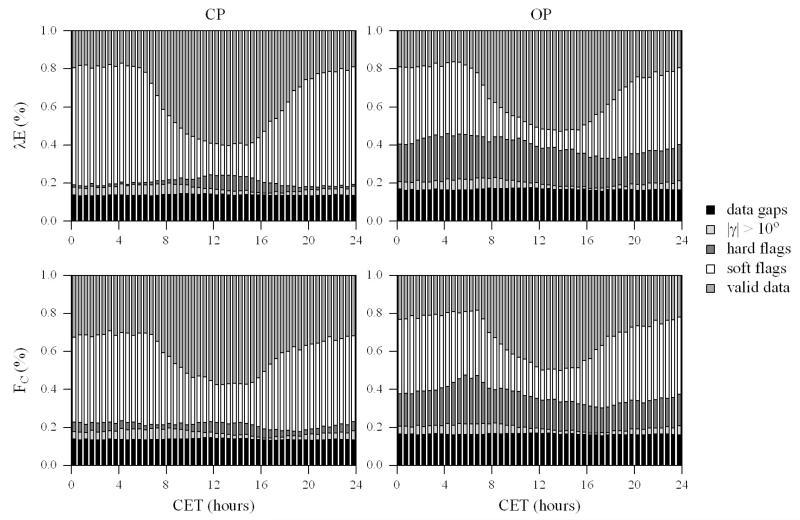
Gap statistics and annual flux estimates

In the six-year study period around 14 and 17 % of the potentially available data were missing due to gaps (instrument malfunction, power outage, failing data storage) for the CP and OP system, respectively. These gaps were largely independent of the time of day (Fig. 6), with 9 and 10 % of gaps occurring in summer (70 % of time) and 25 and 33 % in winter (30 % of time). Around 3 % (mainly during the night and early morning; Fig. 6) of the data (both OP and CP) were excluded because the third rotation angle exceeded ± 10° (McMillen, 1988). Only 3-4 % of the CP data had to be excluded because the CO₂ and H₂O signal, its variation coefficient or the respective fluxes exceeded certain limits (so-called hard-flags), while the same test eliminated 17-20 % of the OP data (Table 1). The fraction of hard-flagged data exhibited a maximum during early morning and a minimum during later afternoon for the OP data, while most of the CP data were excluded for this reason around noon and the least during nighttime (Fig. 6). This difference between the CP and OP system was largely counterbalanced by the so-called soft-flag tests, in particular the stationarity test, which eliminated 28-36 % of the CP, but only 19-21 % of the OP data (Table 1). The fraction of data not complying with the soft-flag tests exhibited a clear diurnal pattern with a maximum during nighttime and a minimum during daytime (both OP and CP system; Fig. 6) and was up to 15 % higher during winter. All together, 36 and 41 % of the CP and 33 and 32 % of the OP data, for latent heat and CO₂ fluxes respectively, passed all quality control tests (Table 1), with 40-50 % and 11-19 % passing in summer and winter, respectively.

Figure 6.

Effect of quality control on percentage data coverage. The various quality control steps have been applied sequentially as they are listed in the legend. Quality control based on absolute concentration and flux limits has been summarised as “hard flags”, the stationarity, integral turbulence and footprint tests as “soft flags”, γ refers to the third angle of the 3D coordinate rotation (Kaimal and Finnigan, 1994). Refer to the text for further details.

Table 1.

Effect of quality control on data coverage (percentage). The various quality control steps have been applied sequentially as they are listed below. Quality control based on absolute concentration and flux limits has been summarised as “hard flags”, γ refers to the third angle of the 3D coordinate rotation (Kaimal and Finnigan, 1994). Refer to the text for further details.

	CP-λE	OP-λE	CP-FC	OP-FC
Missing values	13.7	16.6	13.7	16.4
|γ| > 10°	3.4	3.4	3.4	3.4
CP IRGA pressure	0.1	0.0	0.1	0.0
Hard flags	3.2	19.6	4.0	17.2
Stationarity test	35.6	18.9	27.8	21.3
Integral turbulence test	7.5	8.0	9.2	9.0
Footprint test	0.4	0.7	0.6	0.7
Data gaps	63.9	67.2	58.8	68.0
Valid data	36.1	32.8	41.2	32.0

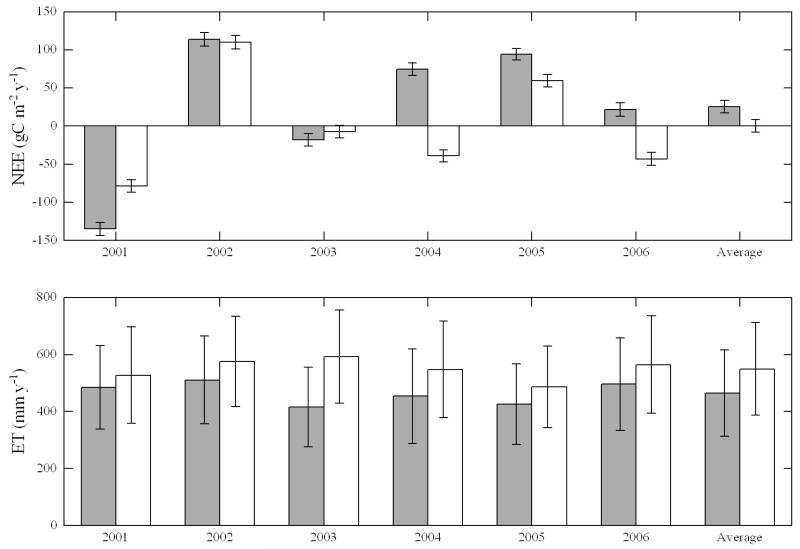
After gap-filling, the annual NEE averaged 25 and 0 gC m⁻² y⁻¹, for the CP and OP system (Fig. 7), respectively, with yearly differences (CP-OP) ranging between −56 (2001) and 114 (2004) gC m⁻² y⁻¹. The CP system consistently yielded lower annual evapotranspiration estimates as compared to the OP system (average of 465 and 549 mm y⁻¹, respectively), with yearly differences ranging between 42 (2001) and 177 (2003) mm y⁻¹ (Fig. 7). Random uncertainties of these annual sums were almost identical for NEE (8.4 and 8.3 gC m⁻² y⁻¹ for the CP and OP system, respectively) and somewhat larger for OP evapotranspiration (151 and 162 mm y⁻¹ for the CP and OP system, respectively).

Figure 7.

Annual sums of CO₂ (upper panel) and H₂O (lower panel) fluxes for the CP (filled bars) and OP (open bars) system for each study year and as an average over all six years. Error bars refer to the random uncertainty of fluxes. Latent heat fluxes were converted from energy to water vapour units by multiplication with the latent heat of vaporisation.

4. Discussion

Post-processing of CP and OP fluxes

The main difference in post-processing of CP as opposed to OP flux data is the need to account for additional low-pass filtering due to tube-related damping and phase shift effects (Massman, 2000), while density corrections are only necessary for water vapour, but not for sensible heat effects (Massman, 2004; Ibrom et al., 2007a). The latter are much more significant for OP systems, where it has been proposed by Burba et al. (2006) it is in addition necessary to account for the sensible heat flux created by the OP IRGA itself, which typically warms above air temperature. Our study confirms that the approach to correct for the effect of low-pass filtering by means of a series of theoretical transfer functions (Moore, 1986; Moncrieff et al., 1997; Aubinet et al., 2000) is able to capture the differential effects of CP and OP systems and accordingly, that, armed with this theory, we are able to successfully correct fluxes for these effects (Wohlfahrt et al., 2005). Given that CP systems suffer from additional low-pass filtering due to tube-related damping and phase shift effects, it may appear counterintuitive that the average frequency response correction factors (1.12-1.15) were not much different between the CP and OP system. This is due to the fact that at low wind speeds low-pass filtering becomes dominated by the effect of lateral sensor separation (Massman, 2000), which was three times larger for the OP (0.3 m) as compared to the CP (0.1 m) system, causing the frequency response correction factor of the OP system to exceed the one of the CP system during calm conditions (Massman, 2000). In addition, low wind speeds tend to occur during stable nighttime conditions, when there is a larger high-frequency contribution to the overall flux (Kaimal and Finnigan, 1994; Wohlfahrt et al., 2005) and thus a larger flux loss (Massman, 2000).

After some recent controversy on the correct mathematical form of the density correction (Liu, 2005; Kowalski, 2006; Massman and Tuovinen, 2006; Kowalski and Serrano-Ortiz, 2007; Leuning, 2007), the theory of Webb et al. (1980) seems now accepted for correcting OP fluxes. Massman (2004) and Ibrom et al. (2007a) showed the need to correct CP flux measurements for water vapour related density fluctuations and proposed methods for doing so. The need to correct OP fluxes for the additional sensible heat flux created by self-heating of the OP IRGA is much less appreciated in the community despite the fact that several authors addressed the issue (e.g. Hirata et al., 2007; Lafleur and Humphreys, 2007; Ono et al., 2007) and Burba et al. (2006, 2008) worked out the theoretical background and proposed practical ways for minimising and correcting for this bias in the field and during post-processing, respectively. This may be due to the fact that while at some sites the correction improved the correspondence between OP and CP fluxes (Burba et al., 2006, 2008; Grelle and Burba, 2007), it changed it for the worse at others (Wohlfahrt et al., 2008b) and had very little effect in the present study (Fig. 2). The causes for these mixed results are unclear at present and clearly more comparisons of this kind at climatologically diverse sites are needed, not least in the light of the ongoing global FLUXNET synthesis activities. Given the minor and inconclusive changes observed in the present study we felt that applying the correction for self-heating was not warranted given the introduction of additional uncertainty (Burba et al., 2008), at least until we are able to confirm the corrections by direct heat flux measurements inside the OP IRGA path (Grelle and Burba, 2007).

With energy balance closures on the order of 75-80 % our study is within the range reported by Wilson et al. (2002) in a survey of 22 FLUXNET sites. The small differences in energy balance closure between the CP and OP system found in our study support recent findings indicating that the widespread lack in energy balance closure does not result from instrumental shortcomings, but is due to unaccounted latent and sensible heat flux contributions at larger spatial and temporal scales (see Foken, 2008 and references therein). We though contend that energy balance closure could be improved somewhat by accounting for heat storage in above-ground biomass or photosynthesis (Jacobs et al., 2008), but this would affect the CP and OP system alike.

Differences between CP and OP fluxes

Similar to the only other study we are aware of that compared CP and OP flux measurements on a long-term basis (2 years; Hirata et al., 2007), we found excellent 1:1 correspondence between CP and OP NEE and latent heat fluxes but also that residuals exhibited a systematic bias. In contrast to Hirata et al. (2007) we observed little bias for the CO₂ flux, but a clear trend of the CP system yielding smaller latent heat fluxes than the OP system during conditions of high air temperature, wind speed and global radiation, large sun angles and low relative humidity (Figs. 3a-b). Along this line it has been recently reported by Ibrom et al. (2007b) that H₂O (but not CO₂; Shimizu, 2007) flux measurements with CP systems may suffer from considerable low-pass filtering (resulting in a flux underestimation) not taken into account by available tube attenuation correction algorithms (e.g. Massman, 1991), as these neglect adsorption/desorption of water vapour to/from the tube walls (Massman and Ibrom, 2008). Yet, in contrast to what might be expected from the analysis of Ibrom et al. (2007b), who showed that low-pass filtering increased with relative humidity, the latent heat flux residuals in our study did not exhibit a strong response to relative humidity (Fig. 3a). This may be due to the confounding effect of wind speed, which is inversely related to relative humidity (p < 0.001) – thus, if an unaccounted high-frequency damping effect exists for the CP H₂O fluxes it will increase with wind speed (Massman, 2000; Ibrom et al., 2007b). However, since high wind speeds tend to occur during conditions of low relative humidity, when low-pass filtering due to adsorption/desorption of water vapour to/from the tube walls plays a minor role (Ibrom et al., 2007b), the humidity effect may be essentially be compensated for by the influence of wind speed. Clearly, this is an issue requiring further research, both with regard to the re-analysis and correction of existing data, as well as the examination of appropriate strategies to avoid the humidity-related low-pass filtering effect (e.g. by using heating to reducing relative air humidity inside the tubing; Ibrom et al., 2007b).

From first principles it is obvious and was confirmed in the present study (Fig. 6, Table 1), that OP systems yield a larger fraction of invalid data due to obstructions of the infra-red path by water or snow as compared to CP systems (see also Mauder et al., 2008), where valid data are often obtained until the sonic data quality becomes compromised by bad weather conditions. Surprisingly, we found that this larger fraction of physically/biologically plausible CP flux data did not translate into a correspondingly larger fraction of accepted flux data, because of a larger fraction of flux data not passing the subsequent quality control steps, in particular the stationarity test (Table 1). In other words – while the CP system yielded more physically plausible data as compared to the OP system, the quality of these additional data was compromised by non-stationarity of the time series and/or deviations from integral similarity characteristics. None the less, the fraction of usable data was larger (up to 10 %) for the CP systems and might have been even larger had we relaxed the quality control criteria, which are comparatively stringent (e.g. Foken et al., 2004). The gap-fraction is important when attempting to derive annual flux budgets, which requires imputation (gap-filling) of data, because the uncertainty of annual flux estimates increases with the gap-fraction (Moffat et al., 2007).

One key application of eddy covariance CO₂, H₂O and energy flux estimates is their assimilation into models which simulate the ecosystem-atmosphere exchange of mass and energy (Raupach et al., 2005). In order to avoid simplifying assumptions in model parameter estimation (e.g. least-squares fitting), the distribution and magnitude of the random flux uncertainties have to be known (Hollinger and Richardson, 2005). Estimates of random flux uncertainties are also required for putting uncertainty bounds on annual flux budgets (Dragoni et al., 2007). The only other study we are aware of that compared CP and OP random flux uncertainties is by Richardson et al. (2006), who, using concurrent CP and OP CO₂ flux measurements above a soybean and maize crop, found the difference in random flux uncertainty to be negligible during daytime, while during nighttime the random uncertainty of the OP system exceeded the one of an CP system by up to 20 %. Our results, in contrast, suggest very small differences in the random flux uncertainty between CP and OP systems (Fig. 5). Richardson et al. (2006) argue that the larger random flux uncertainty of the OP system they observed was due to the effect of sensible heat through the correction for density effects (Webb et al., 1980), in particular during conditions of low CO₂ and large sensible heat fluxes, when the correction may be larger in magnitude than the flux itself (Ham and Heilman, 2003). Since sensible heat fluxes are comparatively small at our site (average midday Bowen ratio of 0.55; Hammerle et al., 2008), this may explain the smaller difference found in the present study.

Implications for flux networks and global synthesis activities

Producing accurate and spatially/temporally consistent flux estimates is one of the major goals of the FLUXNET project (Baldocchi et al., 2001; Baldocchi, 2008) and to this end a standardised protocol is used for flux gap-filling (Papale et al., 2006). For the initial steps of eddy covariance flux acquisition, however, that is raw data acquisition, flux calculation and initial quality control, only recommendations but no standardised protocol exist (Mauder et al., 2008). The difference between the CP and OP system in our study amounted to 25 gC m⁻² y⁻¹ (CO₂) and 84 mm y⁻¹ (H₂O), which resulted from the combination of systematic differences between the two systems (Figs. 3a-b) which propagated into the derivation of annual sums (i.e. gap filling). These differences are on the same order of magnitude as the uncertainty of the algorithms used to fill gaps in EC data sets (Falge et al., 2001b; Moffat et al., 2007) and we thus conclude that whether a CP or OP EC systems is used does not represent a serious source of bias for the present data set. Generalising this result to other study sites is, however, very difficult because multiple, site-specific factors interact in determining the correspondence between CP and OP systems and it will require further long-term comparative studies under differing climatic conditions and over different ecosystems to make progress in this respect. In any case, the basic requirement for avoiding bias between CP and OP systems is to use instrumental setups which minimise all experimental shortcomings and to apply all the necessary post-processing steps, in particular corrections for low-pass filtering (Massman, 2000) and density fluctuations (Webb et al., 1980), to both systems (Mauder et al., 2008). With this regard it appears prudent to further promote approaches such as the AMERIFLUX portable eddy covariance system (Ocheltree and Loescher, 2007) or software inter-comparison activities (Mauder et al., 2008) in order to assure the consistency of data within and across flux networks, in particular as Moffat et al. (2007) have shown that many gap-filling algorithms are already close to the noise limit of the data.