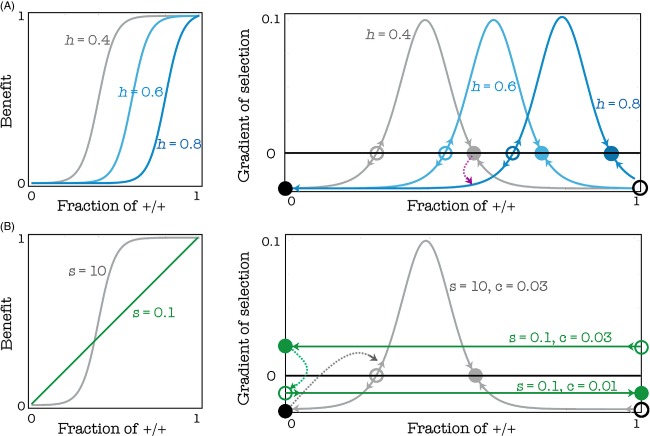
Figure 10.

Dynamics of the evolution of resistance to therapies that target growth factors. In a well-mixed population, the gradient of selection determines the direction of the dynamics: where it is positive, the frequency of producers increases; where it is negative it decreases; equilibria (empty circle: unstable; full circle: stable) are found where the gradient of selection is zero (A) Targeting growth factors directly increases the threshold (h) of the public goods game. The therapy is successful (the +/+ cells go extinct) if the new unstable equilibrium is above the original stable equilibrium; if this is not the case, the system will move to the new internal equilibrium. (c = 0.01, s = 10, n = 50) (B) If the population is at the pure −/− equilibrium, a mutant +/+ can only invade if the cost declines below the gradient of selection, if the benefit function is linear; if the benefit is nonlinear, random fluctuations can allow small clusters of +/+ to invade and thus allow the population to reach the internal stable equilibrium. (h = 0.5, n = 50)