Skip to main content
. 2014 Jan 7;106(1):279–288. doi: 10.1016/j.bpj.2013.10.039

Figure 3.

Figure 3

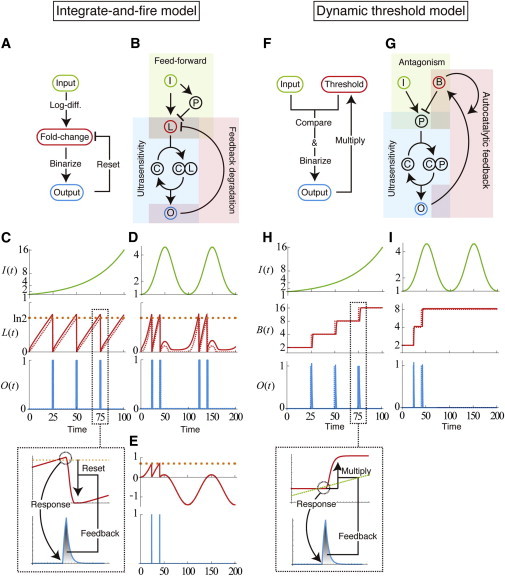
Two possible mechanisms for fold-change detection with specificity and repeatability (srFCD): integrate-and-fire (IF) model and dynamic threshold (DT) model. (A) Logic diagram and (B) biochemical implementation of the IF model. This model consists of three parts: (i) log conversion of input signal I, which is stocked as an internal state L; (ii) binary response O, which depends on the value of L; and (iii) the reset of L after each response through feedback. L is interpreted as the fold-change of input since the last response. After appropriately combining feed-forward and feedback loop motifs, the processes (i–iii) can be biochemically implemented (B). (C and D) Typical responses of the IF model to an exponential input (C) and to a periodic input (D). (Dashed curves) Logic model (see the expressions in Eq. 14); (solid curves) biochemical model (Eq. A1). For a monotonically increasing input, system responses properly occur for every specific-fold change (twofold in this case) in input, but inappropriate responses occur when input includes decreasing phases (D). (E) If L could take negative values, the proper response to a specific-fold change in input would be achieved. (F) Logic diagram and (G) biochemical implementation of the DT model. This model consists of three parts: (i) comparison of the values between input I and an internal state B, which works as a dynamic threshold; (ii) binary response O, which depends on I/B; and (iii) multiplication of the value of B by a constant. The DT model can be biochemically implemented by combining feedback loop motifs (G). (H and I) Typical responses of the DT model to an exponential input (H) and to a periodic input (I); (dashed curves) logic model (see the expressions in Eq. 16); (solid curves) biochemical model (see the expressions in Eq. A2). The DT model can properly detect a specific-fold change in input even with input that includes decreasing phases. The input functions are I(t) = exp(4.0 × 10−2t) (C and H) and I(t) = exp(1.1(1 – cos(2π × 10−2t))) (D and I). To see this figure in color, go online.