Figure 1. Embedding a trajectory in an MSD-network.
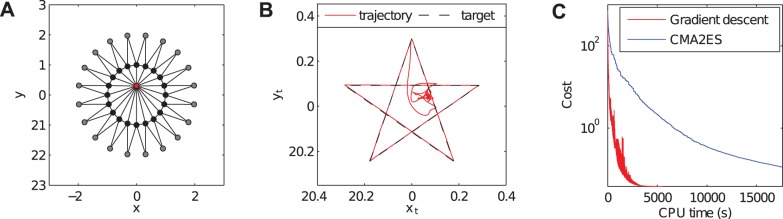
A: Depiction of the initial condition of the MSD-system. The grey circles have fixed positions, the black circles are point masses that are non-fixed, and the red circle is the point mass of which we wish to control the trajectory. The connecting lines represent massless linear spring-dampers. B: Illustration of the trajectory of the selected node after optimisation. The full blue line is the actual trajectory, (including the trajectory after completing the pentagram) and the dashed line is the target. C: Comparison of the convergence speed of gradient descent and CMA-ES for the same initial parameter set.
