Signal-Processing Strategy for Restoration of Cross-Channel Suppression in Hearing-Impaired Listeners

Abstract

Because frequency components interact nonlinearly with each other inside the cochlea, the loudness growth of tones is relatively simple in comparison to the loudness growth of complex sounds. The term suppression refers to a reduction in the response growth of one tone in the presence of a second tone. Suppression is a salient feature of normal cochlear processing and contributes to psychophysical masking. Suppression is evident in many measurements of cochlear function in subjects with normal hearing, including distortion-product otoacoustic emissions (DPOAEs). Suppression is also evident, to a lesser extent, in subjects with mild-to-moderate hearing loss. This paper describes a hearing-aid signal-processing strategy that aims to restore both loudness growth and two-tone suppression in hearing-impaired listeners. The prescription of gain for this strategy is based on measurements of loudness by a method known as categorical loudness scaling. The proposed signal-processing strategy reproduces measured DPOAE suppression tuning curves and generalizes to any number of frequency components. The restoration of both normal suppression and normal loudness has the potential to improve hearing-aid performance and user satisfaction.

I. Introduction

The cochlea is the primary sensory organ for hearing. Its three major signal-processing functions are (1) frequency analysis, (2) dynamic-range compression (DRC), and (3) amplification. The cochlea implements these functions in a concurrent manner that does not allow completely separate characterization of each function. Common forms of hearing loss are manifestations of mutual impairment of these major signal-processing functions. Whenever hearing loss includes the loss of DRC, the application of simple, linear gain in an external hearing aid will not restore normal loudness perception of acoustic signals, which is why nonlinear hearing aids with wide dynamic-range compression are sometimes used to ameliorate this problem.

An important by-product of DRC is suppression, which contributes to psychophysical simultaneous masking (e.g. [1] [2] [3]). Two-tone suppression is a non-linear property of healthy cochleae in which the response (e.g., basilar-membrane displacement and/or neural-firing rate) to a particular frequency is reduced by the simultaneous presence of a second tone at a different frequency [4] [5] [6] [7]. Because these invasive measurements cannot be made in humans, suppression must be estimated by other physiological or psychophysical procedures (e.g. [8] [9] [10] [11] [12]). Distortion product otoacoustic emission (DPOAE) suppression is one of these procedures and can be used to provide a description of the specific suppressive effect of one frequency on another frequency (e.g. [10] [12]).

Suppression plays an important role in the coding of speech and other complex stimuli (e.g. [13]), and it has been suggested to result in enhancement of spectral contrast of complex sounds, such as vowels [14] [15]. This enhancement of spectral contrasts may improve speech perception in the presence of background noise, although only small improvements have been demonstrated thus far [15] [16] [17].

Sensory hearing loss is defined by elevated threshold due to disruption of the major signal-processing functions of the cochlea. Two-tone suppression is usually reduced in ears with sensory hearing loss (e.g. [18] [19]). These ears typically also present with loudness recruitment, a phenomenon where the rate of growth of loudness with increasing sound level is more rapid than normal (e.g. [20] [21]).

Multiband DRC hearing-aids attempt to restore DRC but currently do not attempt to restore normal suppression. DRC alone (i.e., without suppression) may reduce spectral contrasts by reducing gain for spectral peaks while providing greater gain for spectral troughs. This paper describes a hearing-aid signal-processing strategy that aims to restore normal cochlear two-tone suppression, with the expectation that this would improve spectral contrasts for signals such as speech. The implementation of suppression in this strategy was inspired by measurements of DPOAE suppression tuning curves (STC) [22]. The processes of DRC, amplification and suppression are not implemented separately in this strategy, but are unified into a single operation. The prescription of amplification for the method is based on measurements of categorical loudness scaling (CLS) for tones [20] [23], and is intended to restore normal growth of loudness for any type of signal. The strategy is computationally efficient and could be implemented with current hearing-aid technology to restore both normal suppression and normal loudness growth. Restoration of normal suppression may lead to increased hearing-aid user satisfaction and possibly improved speech perception in the presence of background noise. Restoring individualized loudness growth, on the other hand, may increase the usable dynamic range for persons with sensory hearing loss.

DPOAE STCs of Gorga et al. provide a comprehensive description of the specific suppressive effect of one frequency on another frequency [22]. These measurements, which are the basis for the suppression component of the signal-processing strategy, are described in Section II. Use of DPOAE-STC measurements in the calculation of gain allows for the implementation of two-tone suppression.

Al-Salim et al. described a method to determine the level-dependent gain that a hearing-impaired (HI) listener needs in order to have the same loudness percept for tones as a normal-hearing (NH) listener [20]. These data, based on CLS, provide the basis of our amplification-prescription strategy. Specifically, our strategy aims to provide frequency- and level-dependent gain to a HI listener such that a sound that is perceived as “very soft” by a NH listener is also perceived as “very soft” by a HI listener, and a sound that is perceived as “very loud” by a NH listener is also perceived as “very loud” by a HI listener. The idea is to maximize audibility for low-level sounds while at the same time avoiding loudness discomfort at high levels. The hearing-aid fitting strategy requires CLS data at several frequencies for each HI listener. In order to quantify the deviation from normal, average CLS data for NH listeners is also required. Providing frequency- and level-dependent gain allows for the relative loudness of individual frequency components of complex sounds like speech to be preserved after amplification. The goal of restoring normal loudness growth using actual measurements of loudness is in contrast to current hearing aid fitting strategies (e.g. [24] [25]). Current strategies aim to restore audibility and maximize intelligibility, and primarily use hearing thresholds, average population data and generalized models of loudness, instead of individual loudness data, to prescribe gain. While there have been attempts to use individual measurements of loudness and speech intelligibility, these efforts have been used mainly for refining the fit. Another difference between our proposed fitting strategy and most current fitting methods is that our strategy does not use audiometric thresholds, a model of loudness, or a model of speech intelligibility, but uses instead actual CLS data from each HI individual.

This paper describes a novel signal-processing strategy that is motivated by the goals of restoring normal cochlear two-tone suppression and normal loudness growth. The strategy uses a filter-bank to decompose an input signal into multiple channels and a model of two-tone suppression to apply time-varying gain to the output of each channel before subsequently summing these channel outputs. The time-varying gain is designed to implement DRC, amplification and suppression that mimics the way the cochlea performs these functions. These processes are not implemented separately, but concurrently in a unified operation. The gain applied to a particular channel is a function of the levels of all the filter-bank channels, not just that channel. The gains are determined by formulas based on (1) the DPOAE-STC measurements of Gorga et al. [22] and (2) the CLS measurements of Al-Salim et al. [20]. Suppressive effects are applied to these gains instantaneously because measurements of the temporal features of suppression suggest that suppression is essentially instantaneous [26] [27]. Previous studies have suggested that instantaneous compression has deleterious effects on perceived sound quality [28]. In contrast, pilot data from our laboratory have not identified adverse effects on perceived sound quality due to our implementation of instantaneous compression. However, additional data involving more formal and extensive listening tests will be required to corroborate this preliminary observation.

The organization of this paper (after Section I, Introduction) is as follows. Section II describes the DPOAE-STC measurements and how they were used to determine the level-dependent gain that results in two-tone suppression. In Section III, we describe the signal-processing strategy. Signal-processing evaluations to demonstrate (1) nonlinear input/output function, (2) two-tone suppression, (3) STC, and (4) spectral-contrast enhancement are provided in Section IV. Section V describes the use of CLS data for the prescription of amplification. Finally, we discuss and summarize our contributions in Section VI and provide concluding remarks in Section VII.

II. DPOAE Suppression Measurements

The specific influence of suppression of one frequency on another frequency in our signal-processing strategy is based on measurements of DPOAE STCs of Gorga et al. [12] [22]. Therefore, we will first describe these DPOAE measurements before we describe the signal-processing strategy.

In the DPOAE suppression experiments, DPOAEs were elicited in NH human subjects by a pair of primary tones f₁ and f₂ (f₂/f₁ ≈ 1.2), whose levels were held constant while a third, suppressor tone f₃ was presented [12] [22]. The suppressive effect of f₃ was defined as the amount by which its presence reduced the DPOAE level in response to the primary-tone pair. By varying both the frequency and the level of f₃, information about the influence of the frequency relation between suppressor tone and primary tone (mainly f₂) on the amount of suppression was obtained. The DPOAE measurements that are used in the design of the model for human cochlear suppression include eight f₂ frequencies (0.5, 1, 1.4, 2, 2.8, 4, 5.6 and 8 kHz) and primary-tone levels L₂ of 10 to 60 dB sensation level (SL) in 10-dB steps (i.e., relative to each subject’s behavioral threshold). For each f₂ frequency, up to eleven f₃ frequencies surrounding f₂ were used. There are many studies of DPOAE STCs, all of which are in general agreement. However, Gorga et al. provided data for the widest range of frequencies and levels in a large sample of humans with normal hearing. Thus, those data are used as the basis for the signal-processing strategy implemented here.

In DPOAE measurements, the DPOAE level is reduced when a third (suppressor) tone is present, and this reduction is often referred to as a decrement. Let d represent the decrement in DPOAE level due to a suppressor (i.e. d equals the DPOAE level without suppressor minus the DPOAE level with a suppressor). Gorga et al. [12] defined a transformed decrement D as

$$D=10{log}_{10}\left({10}^{d/10}-1\right).$$ (1)

A simple linear regression fit to the transformed decrement D provides slopes of the suppression-growth functions.

Gorga et al. used multiple linear regression to represent the transformed decrement as function of the primary level L₂ and suppressor level L₃ [12] [22]:

$$D=a_1+a_2{L}_2+a_3{L}_3.$$ (2)

In Eq. (2), D has linear dependence on both L₂ and L₃. The regression coefficients (a₁, a₂, a₃) all depend on both the primary frequency f₂ and the suppressor frequency f₃. STCs, such as those shown in Fig. 1, represent the level of the suppressor L₃ at the suppression threshold (i.e., D=0), and are obtained by solving for L₃ in Eq. (2) when D=0 [22]:

$$L_3{|}_{D=0}=-\frac{a_1}{a_3}-\frac{a_2}{a_3}{L}_2.$$ (3)

Fig. 1.

DPOAE STCs for f₂ = 1, 2, 4 and 8 kHz from [22]. The parameter in this figure is f₂ (circles = 1 kHz, triangles = 2 kHz, hourglasses = 4 kHz, and stars = 8 kHz). L₂ ranged from 10 dB SL (lowest STC) to 60 dB SL (highest STC). The unconnected symbols below each set of STCs represent the mean behavioral thresholds for the group of subjects contributing data at that frequency. Adapted from Gorga et al. [22] with permission.

Note that when f₃ ≈ f₂, the first term on the right side of this equation (plotted as isolated symbols in Fig. 1) approximately equals the quiet threshold for a tone at f₃ ≈ f₂. For visual clarity, Fig. 1 shows DPOAE STCs for only a subset of the 8 frequencies for which data are available, f₂ = 1, 2, 4 and 8 kHz. Refer to [22] for the complete set of STCs.

The suppression due to a single tone of the growth of its own cochlear response is what causes its response growth to appear compressive. The relative contribution of a suppressor tone at f₃ to the total compression of a tone at f₂ may be obtained by solving Eq. (3) for L₂ when D=0 :

$$L_2{|}_{D=0}=c_1+c_2{L}_3,$$ (4)

where c₁=−a₁/a₃ and c₂=−a₃/a₂. L₂ as a function of f₃ (in octaves relative f₂) at L₃=40 dB SPL is shown in Fig. 2.

Fig. 2.

Equivalent primary level (dB SL) when suppressor level is 40 dB SPL (see Eq. 4). Note that L₂ appears to have nearly linear dependence on f₃ below f₃ ≈ f₂. We use this trend to generalize the dependence of L₂ on f₂ and f₃ in our extrapolation procedure.

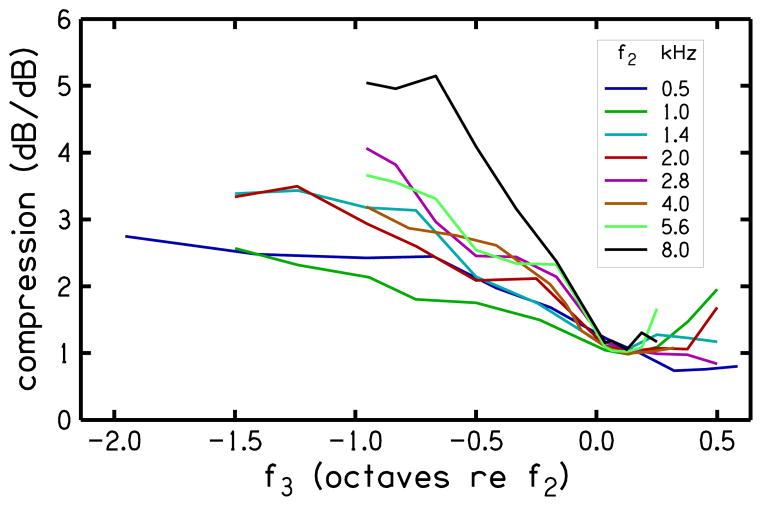
The coefficient c₂ describes the compression of f₂ (relative to compression at f₃) and is plotted in Fig. 3. Note that L₂ and c₂ both have nearly linear dependence on frequency f₃ (when expressed in octaves relative to f₂) below f₃ ≈ f₂ and that c₂ ≈ 1 when f₃ ≈ f₂. We use these trends to generalize the dependences of L₂ and c₂ on f₂ and f₃, and obtain extrapolated c₂ and c₁ [obtained from extrapolated L₂ and c₂ using Eq. (4)] that we use in the signal-processing strategy to determine frequency-dependent gains. Extrapolation of c₂ and c₁ allows application of our signal-processing strategy at any frequency of interest, not just at the frequencies that were used in the DPOAE-STC measurements.

Fig. 3.

Ratio of regression coefficients (c₂₌₋a₃/a₂) from Gorga et al. [22]. c₂ represents compression (dB/dB) as a function of f₃ in octaves relative to f₂. Like L₂, c₂ has a nearly linear dependence on f₃ below f₃ ≈ f₂. We also use this trend to generalize the dependence of c₂ on f₂ and f₃ in our extrapolation procedure. Adapted from Gorga et al. [22] with permission.

The extrapolation is a two-step polynomial-regression procedure that allows for the extension of the representation of c₂ and c₁ from the available (data) frequencies to the desired (model) frequencies. First, separate polynomial regressions were performed to describe the f₃ dependence (of the data shown in Figs. 2 and 3) for both of the coefficients c₂ and L₂ at each of the eight f₂ frequencies. A second set of polynomial regressions were performed to describe the f₂ dependence of the coefficients of the 16 initial polynomials (8 for c₂ and 8 for L₂). The result of this two-step regression was a set of two polynomials that allowed calculation of values for c₁ and c₂ for any desired pair of frequencies f₂ and f₃. Additional constraints were imposed to adjust the calculated values when they did not represent the data. In our current implementation, the two-step regression procedure reduces the representation of c₂ from 88 (8 f₂ × 11 f₃ frequencies) data points down to 10 coefficients and the representation of L₂ from 88 data points down to 15 coefficients.

III. Hearing-Aid Design

Our signal-processing simulation of human cochlear suppression consists of three main stages (as shown in Fig. 4): (1) analysis (2) suppression, and (3) synthesis. In the analysis stage, the input signal is analyzed into multiple frequency bands using a gammatone filterbank. The suppression stage determines the gains that are to be applied to each frequency band in order to achieve both compressive and suppressive effects. In the last stage, the individual outputs of the suppression stage are combined to obtain an output signal that incorporates suppressive effects.

Fig. 4.

Block diagram of model for human cochlear suppression. The model includes three stages (1) analysis using a gammatone filterbank, (2) suppressor stage where frequency-dependent channel gains are calculated and (3) a synthesis stage that combines the output of the suppressor to produces an output signal with suppressive influences.

A. Analysis

Frequency analysis is performed by a complex gammatone filterbank with 31 channels that span the frequency range up to 12 kHz (e.g. [29] [30]). The filterbank design of Hohmann, which requires a complex filterbank, was utilized because of its flexibility in the specification of frequency spacing and bandwidth, while achieving optimally flat group delay across frequency [30]. In our case, the filterbank was designed such that filters above 1 kHz had constant tuning of Q_ERB = 8.65 and center frequencies f_c that are logarithmically spaced with 1/6-octave steps, where Q_ERB is defined as f_c/ERB (f_c) and ERB (f_c) is the equivalent rectangular bandwidth of the filter with center frequency f_c (see [31]). In a design with logarithmically spaced filterbanks, broader filters which are used for high frequencies give shorter processing delay and narrower filters which are used for low frequencies give longer processing delay. To keep the delay at low frequencies within acceptable limits, the filters below 1 kHz were designed to have a constant ERB of 0.1 kHz and linearly spaced center frequencies with 0.1 kHz steps. The filter at 1 kHz had an ERB of 0.11 kHz to create a smooth transition in the transfer function. The individual gammatone filters of the filterbank were fourth-order infinite impulse response (IIR) filters. Filter coefficients were calculated using the gammatone algorithm of Härmä [32].

The outputs of the gammatone filterbank are complex bandpass-filtered time-domain components of the input signal where the real part represents the band-limited gammatone filter output and the imaginary part approximates its Hilbert transform [30]. Thus, complex gammatone filters produce an analytic representation of the signal, which facilitates accurate calculation of the instantaneous time-domain level.

The individual outputs of the filterbank can produce different delays which result in a synthesized output signal with a dispersive impulse response. Compensation for delay of the filters to avoid dispersion is performed in the filterbank stage by adjusting both the fine-structure phase and the envelope delay of each filter’s impulse response so that all channels have their envelope maximum and their fine-structure maximum at the same targeted time instant, (the desired filterbank group delay) [30]. In the current implementation, the target delay was selected to be 4 ms. An advantage of the gammatone filterbank over other frequency-analysis methods (e.g., Fourier transform, continuous wavelet transform) is that it allows frequency resolution to be specified as desired at both low and high frequencies. Also of interest is the fact that gammatone filters are often used in psychophysical auditory models (e.g. [29] [33] [34]) because of their similarity to physiological measures of basilar membrane vibrations (e.g. [35]).

Figure 5 shows the frequency response of the individual gammatone filters (upper panel), and the frequency responses of the output signal and the root-mean-square (rms) levels of the individual filters (middle panel) when the input is an impulse. The frequency response of the output signal, which represents the impulse response, is flat above 0.1 kHz with small oscillations of less than 1.5 dB. The rms level of the individual filters matches the impulse response. The group delay of the impulse response (bottom panel) is nearly a constant 4 ms, as desired. The relatively small oscillation around this constant delay is largest at low frequencies. The group delay achieved by this design is lower than the largest delay that has been shown to be tolerable by hearing-aids users [36] [37].

Fig. 5.

Frequency responses of individual gammatone filters (upper panel), and of the input and output signals (middle panel). Also shown in this panel is the rms level of the individual filters. Lower panel shows delay of the output signal and the acceptable delay hearing aid users. The gammatone filterbank provides a flat magnitude response and acceptable delay for hearing aid users.

B. Suppression

The suppression stage of the model determines gains that are to be applied to each frequency band and that include suppressive effects. The gain applied to a particular frequency band is time-varying and is based on the instantaneous level of every filterbank output in a manner based on measurements of DPOAE STCs. However, unlike in DPOAE suppression measurements where the suppressive effect of a suppressor frequency (f₃) on the DPOAE level in response to two primary tones (f₂ and f₃) was represented, the model represents the influence of a suppressor frequency (f_s) which is equivalent to f₃ on a probe frequency (f_p) which is equivalent to f₂. Henceforth, we will use f_s and f_p in the description of the model.

Suppose that the total suppressive influence on a tone at f of multiple suppressor tones at f_j can be described by summing the individual suppressive intensities of each tone:

$$L_s(f)=10·{log}_{10}\left(\sum _{j=1}^N{10}^{S_j(f)/10}\right),$$ (5)

where

$$S_j(f)=c_1\left(f,f_j\right)+c_2\left(f,f_j\right)·L_j,$$ (6)

represents the individual suppressive level on a tone at f of a single suppressor tones at f_j, and L_j is the filter output level at f_j. The “total suppressive influence” combines the suppressive effect of all frequency components into a single, equivalent level L_s that would cause the same reduction in gain (due to compression) if it was the level of a single tone. Coefficients c₁ and c₂ are derived from the DPOAE data [see Eq. (4)] as described earlier. The sum in Eq. (5) is over all frequency components, including the suppressed tone. The form of Eq. (5) was motivated by the desire to allow a typical decrement function to be reconstructed by subtracting the “control condition,” which is the suppressive level for a one-component stimulus (L_S1), from the “suppressed condition,” which is the suppressive level for a two-component stimulus (L_S1):

$$\begin{array}{c}\mathit{decrement}=L_{S_2}-L_{S_1}=10{log}_{10}\left(\frac{{10}^{S_1/10}+{10}^{S_2/10}}{{10}^{S_1/10}}\right)\\ =10{log}_{10}\left[1+{10}^{(S_2-S_1)/10}\right],\end{array}$$ (7)

Note that Eq. (7) has the form of a typical decrement function when L_S1 fixed and L_S2is varied. The form of Eq. (5) allows the concept of decrement to be generalized to any number of components in the control condition and any number of additional components in the suppressed condition.

Equation (5) describes the suppressive influence of the combination of all suppressor tones. This suppressive level is important in the design of our model. This design requires the specification of c₁ and c₂ for all possible pairs of frequencies in the set of filterbank center frequencies. A reference condition with compression, but no cross-channel suppressive influences, can be achieved by setting L_s(f_j) = L_j. This “compression mode” of operation is useful for evaluating the effects of suppression in our signal-processing strategy. When L_s(f_j) = L_j, according to Eq. (8), the gain G_s to be applied at frequency component f_j is only a function of the level L_j of that component. Eqs. (5) and (6), which bring up the cross-channel suppression, are not involved in the calculation of gain in this case.

Calculation of the frequency-dependent gain from L_s (f) requires specification of four parameters, L_cs (f), L_ce (f), G_cs (f) and G_ce (f) where L_cs and L_ce (such that L_cs < L_ce) are filter output levels, and G_cs and G_ce (such that G_cs > G_ce) are filter gains associated with levels L_cs and L_ce. The subscripts cs and ce, respectively stand for “compression start” and “compression end”, indicating that L_cs is the level where compressive gain is first applied and L_ce is the level at which application of compressive gain ends with corresponding gains G_cs and G_ce. When the filter output level is below L_cs, the filter gain is set to G_cs and the gain is linear (i.e., there is no compression). Above L_ce, the filter gain equals G_ce, and again this gain is linear. That is, linear gain is used below L_cs and above L_ce. When the filter output level is between L_cs and L_ce, filter gain is compressive and decreases as a linear function of the suppressive level. So, the suppressive gain G_s of each filter is a function of suppressive level L_s and has three parts:

$$G_s(L_s)=\{\begin{array}{cc}{G}_{cs}& L_s\le L_{cs}\\ G_{cs}+\left(G_{ce}-G_{cs}\right)\frac{L_s-L_{cs}}{L_{ce}-L_{cs}}& L_{cs}<L_s<L_{ce}\\ G_{ce}& L_s\ge L_{ce}\end{array}.$$ (8)

The dependence of suppressive gain G_s on suppressive level L_s is illustrated in Fig. 6. The two pairs of parameters (L_cs, G_cs) and (L_ce, G_ce) determine the upper and lower knee-points of an input-output function that characterizes the compressive signal processing of the hearing aid. The compression ratio CR in a particular channel when the suppressive level is between L_cs and L_ce is

Fig. 6.

Illustration of suppressive gain G_s (L_s) described by Eq. (8). G_s and L_s are both function of frequency. G_s = G_cs when L_s ≤ L_cs and G_s = G_ce when L_s ≥ L_ce, that is, the gain G_s is linear and non-compressive. For L_cs < L_s < L_ce, the gain G_s is compressive and depends on the suppressive level L_s.

$$CR=1+\frac{G_{ce}-G_{cs}}{L_{ce}-L_{cs}}.$$ (9)

For safety purposes, an additional constraint may be imposed on G_s in the form of a maximum gain G_max defined such that the output level is never greater than a maximum output level L_max in any specific channel. This will avoid loudness discomfort. In a wearable hearing aid, it may also be necessary to reduce G_s at low levels (where G_s is greatest) in order to eliminate acoustic feedback. This issue is further discussed in the Discussion section.

C. Synthesis

In the synthesis stage, the individual outputs of the suppression stage are combined to obtain an output signal with suppressive effects. The combination of the individual frequency bands is designed to produce nearly perfect reconstruction when the suppression applies zero gain to all channels. In this case, the output signal is nearly identical to the input signal, except for a delay that is equal to the filterbank target delay (i.e., 4 ms).

IV. Evaluations

The four tests described below assess the performance of our current MATLAB (The MathWorks, Inc., Natick MA) implementation of the suppression hearing-aid (SHA) signal processing, especially with regard to its ability to reproduce two-tone suppression. For all four tests, the suppressive-gain parameters were set to the following values: L_cs = 0, L_ce = 100, L_max = 115 dB SPL, G_cs= 60 and G_ce = 0 dB. In the simulations to follow, these settings were selected for application of SHA processing to a flat hearing loss of 60 dB.

A. Nonlinear input/output function

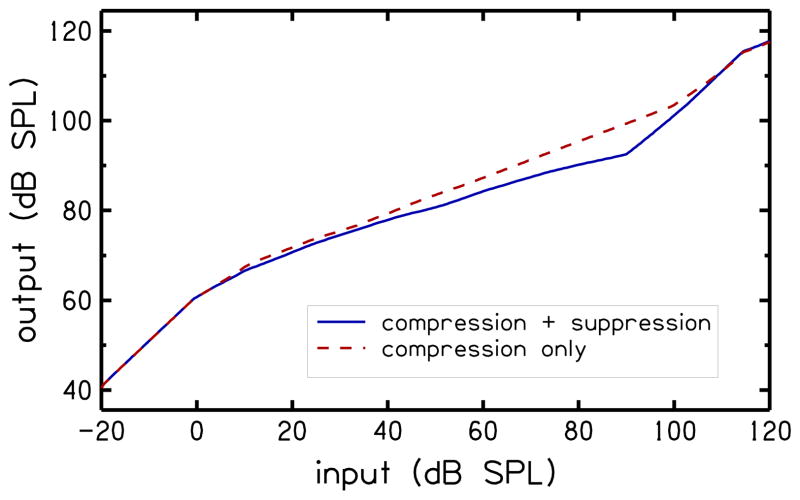
To create an input/output (I/O) function at a specific frequency, a single tone at 4 kHz was input to the SHA simulation, its level varied from −20 to 120 dB SPL, and the level of the 4-kHz component of the output was tracked. I/O functions were created for SHA simulation in normal suppression mode and in channel-specific compression mode (i.e., with no cross-channel suppressive influences).

Figure 7 shows the I/O functions for the two modes of SHA simulation. L_cs = 0 dB SPL and L_ce = 100dB SPL define two knee-points in the I/O function that represent input level where compression starts and ends, respectively. The two I/O functions both have slopes of unity when the input level is less than L_cs = 0dB SPL indicating that G_s = 0dB [cf. Eq. (8)]. Both I/O functions also have unity slopes above L_ce = 100 dB SPL, except that the knee-point for the SHA simulation in suppression mode (solid line) occurs 10 dB below L_ce = 100 dB SPL due to across channel spread in the energy of the 4 kHz tone introduced by Eq. (5). When the input level is between L_cs and L_ce, the slopes of the two I/O functions are both less than unity, with the compression mode having a steeper slope.

Fig. 7.

Input/output functions for model operation in suppression (solid line) and compression (dashed line) modes. Note that the knee points have shifted slightly from their specified levels.

B. Two-tone suppression

To simulate two-tone suppression, a tone pair was input to the SHA simulation. The probe tone was fixed in frequency and level to f_p = 4kHz and L_p = 40dB SPL. The frequency of the suppressor tone was set to f_s = 4.1kHz to simulate “on-frequency” suppression, and to f_s = 2.1 kHz to simulate “off-frequency” suppression. When simulating on-frequency suppression, f_s is set to a frequency that is slightly higher than f_p because if f_s was set equal to f_p then f_s would add to f_p and not suppress f_p. In both on-frequency and off-frequency suppression, the level of the suppressor tone L_s was varied from 0 to 100 dB SPL while tracking the output level at the probe frequency. To obtain an estimate of the amount of suppression produced by the suppressor (the decrement), the output level was subtracted from the output level obtained in the absence of a suppressor tone. Results were generated for SHA simulation in normal suppression mode and in compression mode.

The top panel of Fig. 8 shows decrements for on- and off-frequency suppressors obtained with the suppression mode of model operation. The level of the suppressor needed for onset of suppression is lower in the on-frequency case (L_s ≈ 35 dB SPL) compared to the off-frequency case (L_s ≈ 65 dB SPL). However, once onset of suppression has been reached, suppression grows at a faster rate in the off-frequency case compared to the on-frequency case. These findings are consistent with studies of OAE suppression (e.g. [12] [38]).

Fig. 8.

Decrements for “on-frequency” (solid line) and “off-frequency” (dashed line) suppressor tones when the model is operating in suppression mode (upper panel) and compression mode (lower panel). Cross-channel influences in the calculation of gain for the suppression mode produces the expected behavior for on- and off-frequency suppressors.

The bottom panel of Fig. 8 shows decrements for on-frequency and off-frequency suppressors obtained with the compression mode of model operation. Again, onset of suppression requires a lower suppressor level for the on-frequency case compared to the off-frequency case. However, the level of the suppressor required for onset of suppression in the off-frequency case is much higher and suppression grows at the same rate in both cases. The reason why there is little suppression in the off-frequency case is the lack of cross-channel influences in the calculation of the gain.

C. Suppression tuning curves

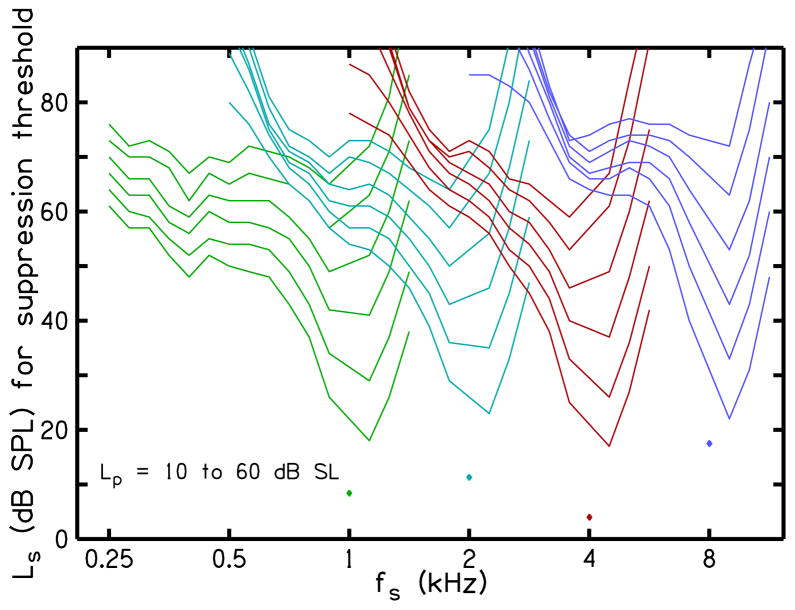
STCs were simulated at four probe frequencies f_p = 1, 2, 4 and 8 kHz, and six probe levels L_p = 10 to 60 dB SL in 10-dB steps. For each f_p, fifteen suppressor frequencies f_s from two octaves below to one octave above the f_p were evaluated. STCs represent the level of the suppressor L_s required for threshold of suppression as a function of f_s. At each f_p and a particular f_s, L_s was varied from L_s = 0 to 100 dB SPL and the suppression threshold [D=0; Eq. (2)] was determined using methods described earlier.

Figure 9 show STCs obtained using the model. These STCs are qualitatively similar to measurements of DPOAE STCs of Gorga et al. [22]. The model STCs are similar to the DPOAE STCs in their absolute level and their dependence on probe-tone level. One difference is that Q_ERB is less dependent on frequency for the model STCs, whereas Q_ERB increases with frequency for the DPOAE STCs. This difference is a consequence of approximations made when fitting suppressor parameters to the DPOAE data; as a consequence, this difference between actual data and model predictions could be reduced by further refinement of these methods.

Fig. 9.

Suppression tuning curves (STCs) obtained using the model for human cochlear suppression. The STCs are qualitatively similar to measurements of DPOAE STCs (see Fig. 1)

D. Spectral contrasts

Enhancement of spectral contrasts potentially could improve speech perception in the presence of background noise [14] [15]. To illustrate the effect of our processing on spectral contrast, Fig. 10 shows the outputs obtained in compression and suppression modes when processing the synthetic vowel /ɑ/ spoken by a male. The pitch of the vowel (F₀) is 124 Hz, and the first three formants are at F₁=730 Hz, F₂=1090 Hz, and F₃=2410 Hz [39]. The solid line is the original vowel (unprocessed input) at a level of 70 dB SPL, a conversational speech level. The dotted line is the output obtained in compression mode and the dashed line is the output obtained in suppression mode. Output vowels obtained with both modes of operation are at a higher SPL compared to the original vowel, as a result of the gain applied. The two outputs are similar in that they both have boosted the level of the third formant relative to the first and second formants. The level of F₀ is also more pronounced in the two outputs compared to the original vowel (peak near 124 Hz in the outputs). Comparing the two outputs, we can see that suppression improves spectral contrast (i.e., the peak-to-trough difference is larger). A spectral-contrast measure was defined as the average of the three formant peaks minus the average of the two intermediate minima, in order to quantify the spectral contrasts of Fig. 10. Spectral-contrast magnitudes are 13.56, 13.84 and 15.30 dB for unprocessed, compression output and suppression output, respectively. Using the spectral-contrast measure, we defined spectral-contrast enhancement (SCE) as spectral contrast for processed minus spectral contrast for unprocessed vowel. Thus, SCE expresses spectral contrast of an output signal relative to that of the input signal. SCE > 0 indicates that the processed signal has enhanced spectral contrast relative to the unprocessed signal. For the example presented here, SCE = 0.28 dB for the output obtained in compression mode and SCE = 1.74 dB for the output obtained in suppression mode. That is, the output obtained in suppression mode results in higher spectral-contrast enhancement compared to either the unprocessed vowel or the output obtained in compression mode.

Fig. 10.

Spectrum of synthetic vowel /ɑ/ spoken by a male after processing using compression mode (dotted line) and suppression mode (dashed line). Solid line is the unprocessed vowel. The input level is 70 dB SPL. Suppression improves spectral contrast by increasing the difference in level between peaks and troughs.

SCE measures for the synthetic vowel /ɑ/ and four other synthetic vowels /i/, /ɪ/, /ε/ and /u/ spoken by male and female speakers are presented in Table I for both the suppression and compression modes of SHA simulation when the input level was 70 dB SPL. The formant frequencies of the vowels (F₀, F₁, F₂ and F₃) are also included in Table I. At the input level of 70 dB SPL, a typical conversational level, processing in suppression mode results in positive SCE for all vowels, except vowel /i/ spoken by a female for which SCE = 0 dB. The mean SCE across the 10 vowels and two genders is 1.78 dB. In contrast, processing in compression mode results in reduction of spectral contrast for most vowels, with a mean SCE of −1.15 dB. Although slightly different from what is used in typical nonlinear hearing-aid signal processing, the results with compression alone provide a first approximation of what might be expected with current processing strategies.

TABLE I.

Spectral Contrast Enhancement (Sce) For Five Synthetic Vowels Spoken By Male And Female Speakers

Vowel	Speaker	F0, F1, F2, F3 (Hz)	SCE (dB)
			Comp	Supp
/i/	Male	136, 270, 2290, 3010	−1.23	1.98
/ɪ/	Male	135, 390, 1990, 2550	1.09	5.08
/ε/	Male	130, 530, 1840, 2480	0.14	3.63
/ɑ/	Male	124, 730, 1090, 2440	0.28	1.74
/u/	Male	141, 300, 870, 2240	−4.07	−0.09
/i/	Female	235, 310, 2790, 3310	−2.93	−1.25
/ɪ/	Female	232, 430, 2480, 3070	−3.64	0.94
/ε/	Female	223, 610, 2330, 2990	0.34	1.57
/ɑ/	Female	212, 850, 1220, 2810	−1.73	2.47
/u/	Female	231, 370, 950, 2670	0.25	1.72
Mean			−1.15	1.78

Comp and Supp denote compression and suppression modes of model operation. The input level is 70 dB SPL.

To summarize the effect of input level on SCE, Fig. 11 shows mean SCE across the 10 synthetic vowels as a function of input level (20 to 100 dB SPL) for the two modes of SHA simulation. SCE for suppression mode (solid line) is greater than zero (indicated by dotted line) and higher than SCE for compression mode (dashed line) across all input levels. SCE for suppression mode reaches a maximum of 4.38 dB at an input level of 85 dB SPL. SCE for compression mode is only greater than zero at low levels (< 33 dB SPL), indicating that the output obtained in this mode deteriorates spectral contrasts that were present in the original signal. The difference in SCE for suppression and compression modes can be as large as 5.81 dB (at an input 85 dB SPL).

Fig. 11.

Mean spectral-contrast enhancement (SCE) across the ten synthetic vowels of Table 1 as a function of input level for output obtained in compression (dashed line) and suppression modes (solid line). Suppression results in spectral contrast enhancement for a wide range of levels.

We also evaluated an alternate measure of SCE based on quality factor (Q_ERB) applied to the formant peaks. The results obtained with this alternate SCE measure were similar to those presented in Table I and Fig. 11, so are not included here.

V. Hearing-aid Fitting Strategy

Our hearing-aid fitting strategy is to provide frequency-dependent gain that restores normal loudness for tones to HI individuals. Specifically, the strategy aims to provide gain such that a tone that is perceived as ‘very soft’ by a NH individual is also perceived as ‘very soft’ by a HI individual, and a tone that is perceived as ‘very loud’ by a NH individual is also perceived as ‘very loud’ by a HI individual. The idea is to maximize audibility for low-level sounds while avoiding loudness discomfort at high levels. It is expected that this amount of gain will be too much for sounds other than pure tones; however, suppression will provide gain reduction in the hearing aid in the same way that suppression reduces gain in the normally functioning cochlea. Additionally, a maximum gain can be specified to avoid loudness discomfort at high levels, as described in Section III.

Our signal-processing strategy only suppresses the gain that it provides. We assume that the impaired ear will continue to suppress any residual outer hair cell (OHC) gain that it still possesses. In combination, suppression is divided between the external aid and the inner ear in the same proportion as their respective contributions to the total gain.

The hearing-aid fitting strategy requires CLS data at several test frequencies for the HI individual being fitted with the hearing-aid and average CLS data at the same frequencies for NH listeners. The CLS test described by Al-Salim et al. [20] is used in our fitting strategy. This test determines the input level of a pure tone that is associated with each of the eleven loudness categories at several test frequencies. Only seven of the eleven categories are labeled, but all have an associated numerical categorical-unit (CU) value. Meaningful adjectives (e.g., ‘soft’, ‘medium’, ‘loud’) are used as labels, consistent with the international standard for CLS [40]. Given the relationship between gain and CLS categories (described by Al-Salim et al. [20]), we only used ‘very soft’ (CU = 5) and ‘very loud’ (CU = 45) for the hearing-aid fitting strategy.

A method to determine gain from CLS data was suggested by Al-Salim et al. [20]. In this method, average CLS data for NH is used to determine reference input level for a given loudness category that should be attained to restore normal loudness for HI individuals through the application of gain. The gain required to elicit the same loudness percept in HI listeners as in NH listeners is then the difference between the normal reference input level and the input level required by HI listeners to achieve the same loudness percept. The input levels for these categories will be represented by L_vs,NH and L_vl,NH for NH, and by L_vs,HI and L_vl,HI for HI. The input levels L_vs,NH and L_vl,NH at 1 kHz for the current simulation are based on CLS data of Al-Salim [20]. The values of L_vs,NH and L_vl,NH at other frequencies are taken from equal-loudness contours [41] at phons that correspond to average SPL values of L_vs,NH and L_vl,NH. This method of extrapolation is valid because an equal-loudness contour (by definition) represents the sound pressure in dB SPL as a function of frequency that a NH listener perceives as having a constant loudness for pure-tone stimuli. Examples of L_vs,NH and L_vl,NH loudness contours are shown in the top panel of Fig. 12 (dashed lines) based on the average CLS data of Al-Salim et al. At 1 kHz, average values for ‘very soft’ and ‘very loud’ categories were L_vs,NH = 22.9 and L_vl,NH = 100.1 dB SPL, respectively. Thus, by definition, the corresponding loudness contours (dashed lines) represent loudness levels of 22.9 and 100.1 phons. For comparison, Fig. 12 also shows that the average levels (filled symbols, top panel) associated with ‘very soft’ and ‘very loud’ at the other two frequencies (2 and 4 kHz) tested by Al-Salim et al. [20]. The closeness of these symbols to the dashed lines demonstrates agreement between the measurements and the loudness contours.

Fig. 12.

Input levels L_{vs NH}, L_{vl NH}, L_{vs HI} and L_vl,HI, and their extrapolations (top panel). Gains G_cs and G_ce determined from the input levels (bottom panel).

To further describe our proposed hearing-aid fitting strategy, the top panel of Fig. 12 also shows input levels L_vs,HI and L_vl,HI for a hypothetical HI individual with CLS data at 0.25, 0.5, 1, 2, 4 and 8 kHz (open symbols). Values of L_vs,HI and L_vl,HI for the specific filterbank frequencies used in our SHA simulation are obtained by interpolation and extrapolation. In this example, the input level required for the loudness category ‘very soft’ is higher for the HI individual compared to the NH individual, especially at high frequencies. However, the input levels required for the loudness category ‘very loud’ are close to the NH contours. The difference between L_vs,HI and L_vs,NH is the gain required for this hypothetical HI individual to restore normal loudness of ‘very soft’ sounds, and the difference between L_vl,HI and L_vl,NH is the gain required to restore normal loudness of ‘very loud’ sounds. In terms of the gain calculation of Eq. (8), these gains, and their associated input levels are

$$\begin{array}{c}{G}_{cs}=L_{vs,HI}-L_{vs,NH}\\ G_{ce}=L_{vl,HI}-L_{vl,NH}\\ L_{cs}=L_{vs,NH}\\ L_{ce}=L_{vl,NH}\end{array}$$ (10)

The bottom panel of Fig. 12 shows gains G_cs and G_ce as function of frequency. The gain G_cs is larger at high frequencies compared to low frequencies. The gain G_ce is small (range of only 6 dB) and near constant with frequency since the levels L_vl,HI and L_vl,NH are similar. The particular frequency dependence of gains G_cs and G_ce are each determined by the “deficit” from the normal “reference” input levels of the particular HI individual.

VI. Discussion

The idea of restoring normal two-tone suppression through a hearing aid has been proposed before. Turicchia and Sarpeshkar described a strategy for restoring effects of two-tone suppression in hearing-impaired individuals that uses multiband compression followed by expansion [14]. The compressing-and-expanding (companding) can lead to two-tone suppression in the following manner. For a given band, a broadband filter was used for the compression stage and a narrowband filter for the expansion stage. An intense tone with a frequency outside the narrowband filter passband of the expander but within the passband of the broadband filter of the compressor results in a reduction of the level of a tone at the frequency of the expander but is then filtered out by the narrowband expander, producing two-tone suppression effects. They suggested that parameters for their system can be selected to mimic the auditory system; however, this was not demonstrated. Subsequent evaluation of their strategy only resulted in small improvements in speech intelligibility [15] [16].

Strelcyk et al. described an approach to restore loudness growth restoration of normal loudness summation and differential loudness [42]. Loudness summation is a phenomenon where a broadband sound is perceived as being louder than a narrowband sound when the two sounds have identical sound pressure level. Loudness summation is achieved in the system of Strelcyk et al. by widening the bandwidth of channel filters as level increases.

Our hearing-aid signal-processing strategy performs two-tone suppression by considering the instantaneous output of all frequency channels when calculating the gain for a particular channel. This cross-channel influence in the calculation of gain is based on DPOAE-STC measurements and is applied instantaneously. Our strategy has greater ecological validity compared to the method of Turicchia and Sarpeshkar [14], which was also intended to restore two-tone suppression, because our design is based on DPOAE-STC data from NH subjects, whereas their design was not based on two-tone suppression data. However, benefits from our processing strategy in terms of listener preference and speech intelligibility have not yet been demonstrated, but studies are under way to determine the extent of the benefits. The data from those studies will be presented upon their completion.

In addition to the aim of restoring two-tone suppression, our strategy also aims at restoring normal loudness growth through the use of individual measurements of CLS. Although restoration of loudness through a hearing aid has been proposed before (e.g. [43] [44] [45]), it has never been clear how to use narrowband loudness data to prescribe amplification that restores normal loudness for complex sounds. Furthermore, concerns have been raised regarding gain for low-level inputs because HI listeners frequently complain that such an approach makes background noise loud. Our approach of using two-tone suppression to extend loudness-growth restoration to complex sounds is novel, and has the potential to control issues associated with amplified background noise, while still making low-level sounds audible for HI listeners in the absence of background noise.

Our working hypothesis is that loss of suppression is a significant contributor to abnormal loudness summation in HI ears. Therefore, integration of suppression and nonlinear gain based on loudness of single tones has the potential to compensate for loudness summation. The loudness data used for prescribing gain defines the level of a single tone that will restore normal loudness in HI individuals. The suppression describes how the level of one tone affects the level of another tone at a different frequency. We expect that this combined effect will generalize to loudness restoration for broadband stimuli, thus compensating for loudness summation.

The performance of our signal-processing strategy was demonstrated by showing results of a SHA simulation. This simulation produces STCs that are qualitatively similar to DPOAE-STCs data (compare Figs. 1 and 9). The SHA simulation also provides enhancement of spectral contrast (see Figs. 10 and 11), which potentially will improve speech perception in the presence of background noise. For the set of vowels used here to evaluate spectral-contrast enhancement, the largest SCE was obtained at an input level of 85 dB SPL, a level that is greater than conversational speech level. Above this level, SCE decreased but was still greater than zero. This is a promising result because it shows that our strategy might be able to provide speech-perception benefits for a range of speech levels that include levels mostly encountered for speech.

Previous studies have shown that consonant identification is more critical for speech perception, compared to vowel identification, especially in the presence of background noise (e.g. [46]), and that signal-processing strategies aimed at enhancing consonants and other transient parts of speech can improve speech perception in the presence of background noise (e.g. [47]). Our present strategy does not aim to enhance consonants but aims to restore normal cochlear suppression. The overarching goal of this study was to focus on restoration of cochlear processes that are diminished with hearing loss, including suppression and compression. In turn, their restoration may improve speech perception and/or sound quality. At the very least, it is reasonable to predict that the instantaneous compression and flat group delay of our strategy will preserve transients in the presence of background noise.

The implementation of suppression in our hearing-aid signal-processing strategy is based on DPOAE STC measurements. DPOAE STCs might underestimate suppression and tuning because of the three-tone stimulus that is used during their measurement. In fact, data have suggested that stimulus-frequency OAE (SFOAE) suppression tuning is sharper [48]. Therefore, DPOAE STCs might not be the best basis for suppression. It would be interesting to evaluate the benefit of sharper tuning in our implementation of suppression.

Our hearing-aid fitting strategy requires normative reference loudness functions to determine the gain required for an individual HI individual. This normative reference should be constructed with care as loudness scaling data are characterized by variability, especially across different scaling procedures [49]. However, Al-Salim et al. [20] demonstrated that loudness scaling data for a single procedure can be reliable and repeatable, with variability (standard deviation of the mean difference between sessions) that is similar to that of audiometric thresholds.

The aim of our hearing-aid fitting strategy is to restore normal loudness in HI individuals by providing gain to a HI individual such that a tone that is perceived as ‘very soft’ by a NH individual is also perceived as ‘very soft’ by a HI individual, and a tone that is perceived as ‘very loud’ by a NH individual is also perceived as ‘very loud’ by a HI individual. Using two end-points in the gain calculation assumes a linear CLS function for a HI individual. However, a typical CLS function is often characterized by two distinct linear segments connected around ‘medium’ loudness (e.g. [20] [23] [40]). In the future, we plan to include a third category, ‘medium’ loudness in our fitting strategy (i.e., provide gain to HI individual such that a tone that is perceived as ‘medium’ by a NH individual is also perceived as ‘medium’ by a HI individual). Cox considered a similar approach in her loudness-based fitting strategy [45].

The gain required to restore normal loudness of “very soft” sounds G_cs may result in acoustic feedback. This feedback can be reduced or eliminated by requiring that G_cs in one or more channels be reduced below what would otherwise be required to restore normal loudness of “very soft” sounds; that is, G_cs should be less than Ḡ_max, where Ḡ_max is a maximum gain that does not result in feedback. This may be done by selecting a new knee-point L_cs that achieves the desired G_cs≤Ḡ_max without altering the desired input-gain function at levels above the new L_cs. In this way, our processing strategy is easily adapted to constraints imposed by the need to eliminate feedback, while still restoring normal cross-channel suppression at higher levels. The impact of feedback on our signal-processing strategy could also be reduced by avoiding “open canal” hearing-aid designs for moderate or greater hearing losses. “Open canal” hearing aids result in more feedback because the opening allows the hearing-aid microphone to pick up sound from the receiver.

The goal of the proposed signal-processing strategy is to compensate for effects due to OHC damage which diminishes suppression and dynamic range and results in loudness recruitment. OHC damage results in no more than about a 60-dB loss; as a result, the algorithm is designed to ameliorate consequences from hearing losses less than or equal to 60 dB. It is not designed to ameliorate problems associated with inner hair cell damage or damage to primary afferent fibers, which are typically associated with greater degrees of hearing loss. Alternate and/or additional strategies will be needed to provide relief in these cases. It is possible that some combination of strategies that include SHA processing might be shown to provide benefit in these cases as well. However, at this point, our focus is on a signal-processing strategy that will overcome consequences of mild-to-moderate hearing loss due to OHC damage.

Our processing strategy incorporates methods that restore both normal suppression and loudness growth. To a first approximation, the amount of forward masking depends on the response to the masker and is thought to reflect short-term adaptation processes mediated at the level of the hair-cell/afferent fiber synapse. To the extent that our implementation controls gain, it also will control the response elicited by any signal. In turn, it is expected that compressive gain will also influence adaptation effects at the synapse and perhaps influence forward masking through this mechanism. It is still possible that our signal processing will cause forward and backward masking to become closer to normal by quickly restoring normal loudness as a function of time. Confirmation of this hypothesis will require further testing.

Important issues that will need to be considered before implementing our strategy in hearing-aid hardware include computational efficiency and power consumption. In a hearing aid, every computation draws power from the battery, so computational efficiency is important for maximizing battery life. The gammatone filters of our filterbank were implemented using fourth-order IIR filters. In general, a fourth-order IIR filter has five coefficients in the numerator and five coefficients in the denominator. Application of the filter requires a multiplication operation for each coefficient. The coefficients are typically normalized so that the first denominator coefficient equals 1, requiring 9 potential multiplications. Two of the numerator coefficients in our gammatone filters are always zero. Therefore, our gammatone filters require seven complex multiplications per sample or 14 real multiplications per sample. With 31 channels and a sampling rate of 24 kHz, our gammatone filterbank requires 434 multiplications per sample or about 10.4 million multiplications per second for a 12-kHz bandwidth. There are various ways to reduce the number of multiplications per second, which would increase computational efficiency and thereby reduce power consumption. For example, a 6-kHz bandwidth, which requires only 25 channels and a sampling rate of 12-kHz, would reduce the number of multiplications at the filterbank stage to about 4.2 million multiplications per second. Herzke and Hohmann outlined additional strategies for improving the computational efficiency of the gammatone filterbank [28].

Further computational efficiency can be achieved by making changes to the suppressor stage of our model. Instead of calculating and applying gain on a sample- by-sample basis, some form of efficient down-sampling that is transparent to the output signal may be applied. In our current implementation, the computation time required by the suppression stage is approximately equal to the computation time required by the filterbank. Through simulations using the full filterbank (31 channels and a sampling rate of 24 kHz), we were able to reduce the number of floating-point operations per second (flops, as reported by MATLAB) from 255 Mflops to 108 Mflops by down-sampling the gain calculation by a factor of six. Computational efficiency can be improved further by limiting the number of channels that are used for calculating the suppressive level in Eq. (5). The strategies outlined here, and possibly others, will be useful when implementing our signal-processing strategy in hardware that may be applicable to hearing aids.

VII. Conclusion

Our hearing-aid signal-processing strategy unifies compression with cross-channel interaction in its calculation of level-dependent gain. In this combined model, gain at each frequency is dependent to varying degrees on the instantaneous level of frequency components across the entire audible range of frequencies, in a manner that realizes cochlear-like two-tone suppression. The similarity of this model to cochlear suppression is demonstrated in the similarity of simulated STCs to measured DPOAE STCs in humans with NH. Although not specifically an element of the design, the presence of suppression apparently results in the preservation of local spectral contrasts, which may be useful for speech perception in background noise. The proposed strategy is computationally efficient enough for real-time implementation with current hearing-aid technologies. Benefits in terms of listener preference and speech intelligibility have not yet been demonstrated, but are expected as results of further studies become available.

Biographies

Daniel M. Rasetshwane (M’08) received his degrees in Electrical Engineering from the University of Pittsburgh (BS ’02, MS ’05, PhD ’09). His graduate research focused on speech processing for intelligibility enhancement. He is currently a Research Engineer at Boys Town National Research Hospital’s Center for Hearing Research. His research interests include signal processing for hearing prostheses, acoustic reflectance, otoacoustic emissions, and cochlear mechanics.

Michael P. Gorga is a clinical audiologist and director of the Clinical Sensory Physiology Lab at Boys Town National Research Hospital. He received his degrees in Audiology and Hearing Science from Brooklyn College (BA ’72, MA ’76) and from the University of Iowa (PhD ’80). His interests are in understanding cochlear function in humans with hearing loss, using electrophysiological and acoustical techniques.

Stephen T. Neely (M’75) has been a staff scientist at the Boys Town National Research Hospital since 1982. His graduate work in Electrical Engineering at the California Institute of Technology (MS’75-Engr’78) and Washington University (DSc’81) focused on mathematical modeling and computer simulation of cochlear mechanics. His other research interests include otoacoustic emissions, loudness theory, wave propagation, and auditory signal processing.