Figure 2.

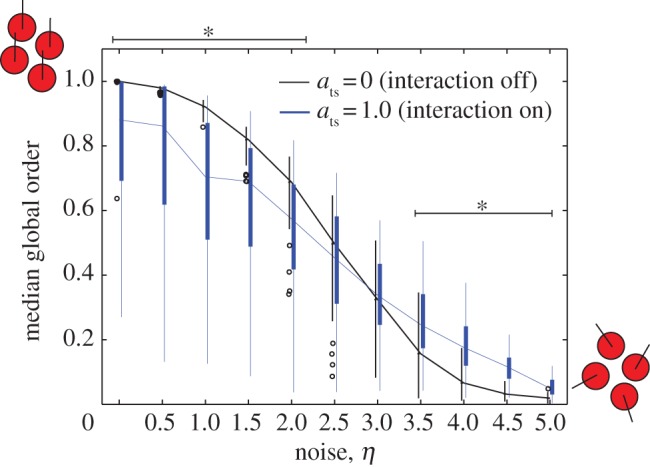
Global order parameter as a function of noise in a system with cyclic boundary conditions. Under a fixed value of a_ts, as η is increased, the system exhibits a phase transition from ordered (global order parameter approx. 1) to disordered (global order parameter approx. 0). When a_ts = 0, the phase transition occurs as in ref. [8]. When a_ts = 1.0, global order is decreased for low values of η, but increased for high values of η compared with the a_ts = 0 system. Asterisks indicate a significant difference between the a_ts = 1.0 and a_ts = 0 simulations (p < 0.001).