Significance
Linear expansions in basis functions are used to approximate continuous functions in many areas of engineering, science, and mathematics. Plane waves are perhaps the most widely used example of a general basis that is both simple and efficient. However, individual plane waves are spatially delocalized, and hence a large number of basis functions become necessary to describe rapidly varying phenomena. We propose a generalization of the plane wave basis, called compressed plane waves, which combine multiresolution properties in both time and frequency domains. These functions are derived from an  regularized variational principle for a differential operator (Laplacian) and can efficiently represent functions which contain both slowly and rapidly varying features.
regularized variational principle for a differential operator (Laplacian) and can efficiently represent functions which contain both slowly and rapidly varying features.
Abstract
This paper describes an 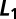 regularized variational framework for developing a spatially localized basis, compressed plane waves, that spans the eigenspace of a differential operator, for instance, the Laplace operator. Our approach generalizes the concept of plane waves to an orthogonal real-space basis with multiresolution capabilities.
regularized variational framework for developing a spatially localized basis, compressed plane waves, that spans the eigenspace of a differential operator, for instance, the Laplace operator. Our approach generalizes the concept of plane waves to an orthogonal real-space basis with multiresolution capabilities.
Generality, conceptual simplicity, and development of efficient numerical algorithms based on the fast Fourier transform (FFT) have facilitated the adoption of plane waves as canonical basis functions for countless applications in engineering, science, and mathematics (1, 2). Since the plane waves are continuously differentiable eigenfunctions of the Laplace operator, they are well suited for representing solutions to partial differential equations (PDEs) of mathematical physics, such as those arising in quantum mechanics and electrodynamics. One of the most attractive features of plane waves is the ability to systematically increase spatial (or temporal) resolution by including higher kinetic energy (or frequency) components. However, since the plane waves are global functions, resolution is increased uniformly throughout the entire space, while, in practice, high resolution may be required only in a small fraction of the problem domain. The need for functions that can represent multiple length scales has spurred the development of wavelets (3), which are localized basis functions with multiresolution capabilities. Wavelets have been tremendously successful in fields such as signal processing, image science, and data science, but adoption of wavelets as the basis for solving PDEs has been difficult because it is numerically complicated to evaluate the derivative of a wavelet in a wavelet expansion. Furthermore, canonical wavelet functions usually can only be defined on regular domains in 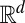 by tensor products of wavelets in one dimension (1D), which makes them difficult to generalize to irregular domains.
by tensor products of wavelets in one dimension (1D), which makes them difficult to generalize to irregular domains.
In this paper, we extend our earlier work in ref. 4 and propose a method for generating a localized orthonormal basis that is adapted to a given differential operator, in particular, the Laplace operator. In ref. 4, we showed that 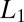 regularization of the variational formulation of the Schrödinger equation of quantum mechanics can be used to create compressed modes, a set of spatially localized functions
regularization of the variational formulation of the Schrödinger equation of quantum mechanics can be used to create compressed modes, a set of spatially localized functions 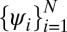 in
in 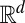 with compact support:
with compact support:
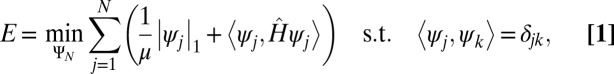 |
where 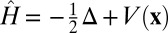 is the Hamilton operator corresponding to potential
is the Hamilton operator corresponding to potential 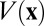 ,
, 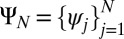 are variational single-particle orbitals, and
are variational single-particle orbitals, and 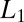 norm is defined as
norm is defined as 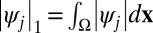 . This
. This 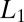 regularized variational approach describes a general formalism for obtaining localized (in fact, compactly supported) solutions to a class of mathematical physics PDEs, which can be recast as variational optimization problems. One of the main advantages of this variational approach is that one parameter μ controls both the physical accuracy and the spatial extent of the resulting solutions: The wave functions
regularized variational approach describes a general formalism for obtaining localized (in fact, compactly supported) solutions to a class of mathematical physics PDEs, which can be recast as variational optimization problems. One of the main advantages of this variational approach is that one parameter μ controls both the physical accuracy and the spatial extent of the resulting solutions: The wave functions 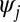 are nonzero only where required to achieve a given accuracy for the total energy and are zero everywhere else. Another advantage of our
are nonzero only where required to achieve a given accuracy for the total energy and are zero everywhere else. Another advantage of our 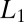 regularized variational method is its natural adaptability to irregular domains in
regularized variational method is its natural adaptability to irregular domains in 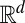 , manifolds, and graphs.
, manifolds, and graphs.
As a major contribution of this paper, we develop a variational framework for generating a set of compactly supported orthonormal basis functions by applying the 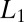 regularized variational method of Eq. 1 to the free particle case when
regularized variational method of Eq. 1 to the free particle case when 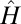 is given by the Laplace operator. This basis has multiresolution capabilities and is expected to be generally useful for representing functions with localized sharp features, especially for solutions to PDEs with the Laplace operator. Orthogonality is imposed in the manner of ref. 5 for shift-orthogonal wavelets, which, in the context of our approach, means that the basis functions are orthogonal to their translations by all vectors belonging to a given lattice (Eq. 2). In addition to shift orthogonality, we introduce a hierarchy of compressed waves obtained from the variational formula, which provides different scales of multiresolution analysis. This is accomplished by enforcing additional orthogonality constraints on
is given by the Laplace operator. This basis has multiresolution capabilities and is expected to be generally useful for representing functions with localized sharp features, especially for solutions to PDEs with the Laplace operator. Orthogonality is imposed in the manner of ref. 5 for shift-orthogonal wavelets, which, in the context of our approach, means that the basis functions are orthogonal to their translations by all vectors belonging to a given lattice (Eq. 2). In addition to shift orthogonality, we introduce a hierarchy of compressed waves obtained from the variational formula, which provides different scales of multiresolution analysis. This is accomplished by enforcing additional orthogonality constraints on 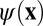 in the variational model Eq. 1, expressed below by the variational formulas Eqs. 3 and 4. As discussed in ref. 4, the properties of
in the variational model Eq. 1, expressed below by the variational formulas Eqs. 3 and 4. As discussed in ref. 4, the properties of 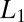 regularization ensure that the resulting functions have compact support in real space. These functions are referred to as basic compressed plane waves (BCPWs). A complete basis set of orthonormal compressed plane waves (CPWs) can be generated from the BCPWs by translations on a d-dimensional lattice. In contrast to approaches for generating localized basis in high dimension using tensor products of 1D basis functions, our variational method provides a direct method to create a localized basis in high-dimensional space. Moreover, this framework can also be naturally extended to more general elliptic operators. A numerical algorithm is designed to efficiently solve the nonconvex optimization problem for constructing BCPWs, and a fast CPW transform and fast inverse CPW transform are developed for transforming between frequency space and real space. Numerical experiments demonstrate that CPWs can efficiently represent spatially localized functions, suggesting advantages over canonical bases of extended functions such as plane waves.
regularization ensure that the resulting functions have compact support in real space. These functions are referred to as basic compressed plane waves (BCPWs). A complete basis set of orthonormal compressed plane waves (CPWs) can be generated from the BCPWs by translations on a d-dimensional lattice. In contrast to approaches for generating localized basis in high dimension using tensor products of 1D basis functions, our variational method provides a direct method to create a localized basis in high-dimensional space. Moreover, this framework can also be naturally extended to more general elliptic operators. A numerical algorithm is designed to efficiently solve the nonconvex optimization problem for constructing BCPWs, and a fast CPW transform and fast inverse CPW transform are developed for transforming between frequency space and real space. Numerical experiments demonstrate that CPWs can efficiently represent spatially localized functions, suggesting advantages over canonical bases of extended functions such as plane waves.
Compressed Plane Waves
We consider an elliptic Hamilton operator 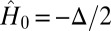 defined in
defined in 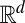 , which describes the movement of free electrons. Let
, which describes the movement of free electrons. Let 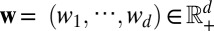 be a basis of a d-dimensional lattice,
be a basis of a d-dimensional lattice,
Inspired by the variational model for compressed modes (CMs) introduced in ref. 4, we introduce a set of localized orthonormal functions 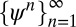 defined by:
defined by:
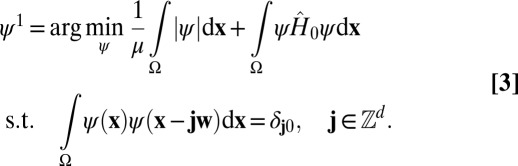 |
The higher modes can be recursively defined as:
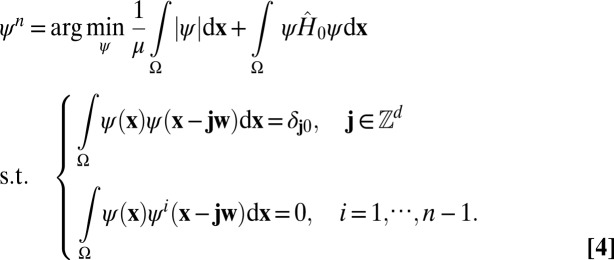 |
Here, the parameters μ and w are given. With the help of the localized orthonormal modes 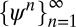 , we can construct a set of orthonormal functions as follows.
, we can construct a set of orthonormal functions as follows.
Definition 1.
We define
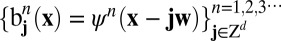 . We call
. We call
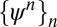 the basic compressed plane waves (BCPWs) and call
the basic compressed plane waves (BCPWs) and call
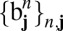 the compressed plane waves (CPWs).
the compressed plane waves (CPWs).
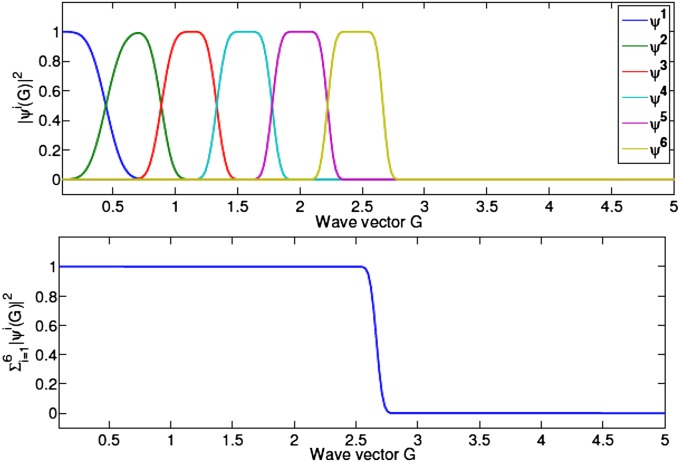
Based on our numerical experiments (see Fig. 2), we expect that the CPWs are complete and form an orthonormal basis. We formulate the following conjecture for the completeness of CPWs, which will be studied in future work.
Fig. 2.
Spectral density distribution of CPWs. (Upper) The spectral density distribution of 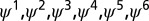 . (Lower) The total spectral density distribution of the first four modes.
. (Lower) The total spectral density distribution of the first four modes.
Conjecture 1 (Completeness of CPWs).
There exists a constant
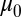 such that the set of orthonormal functions
such that the set of orthonormal functions
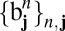 generated from
Eqs.
3
and
4
is complete for any
generated from
Eqs.
3
and
4
is complete for any
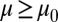 .
.
The proposed method for constructing CPWs in high dimensions is essentially different from the usual way of generalizing a 1D basis to the multidimensional case using the tensor product. Moreover, it is also clear that the index n controls the size of the compact support and the scale of CPWs, while j controls the shift. These two parameters are analogous to the scale and shift parameters in the wavelet theory, which in the future might help in building a new method of multiresolution analysis. In addition, the following scaling formula, which can be obtained by a simple change of variables, indicates the relation between the parameter μ and the lattice basis w.
Property 1. (Scaling formula)
If we write
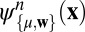 as the n-th BCPW obtained from
Eqs.
3
and
4
with parameters
as the n-th BCPW obtained from
Eqs.
3
and
4
with parameters
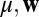 , then the following formula holds for BCPWs
, then the following formula holds for BCPWs
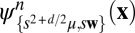 defined on scaled lattice
defined on scaled lattice
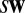 :
:
We would like to point out that the variational framework proposed here can also be extended to a general Hamilton operator with nonzero potential function 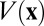 .
.
Numerical Algorithms for Constructing CPWs
To simplify our discussion, we only consider 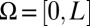 in 1D with periodic boundary conditions; the algorithms for optimization problems Eqs. 3 and 4, as well as the fast transforms discussed below, can be straightforwardly extended to higher dimensions.
in 1D with periodic boundary conditions; the algorithms for optimization problems Eqs. 3 and 4, as well as the fast transforms discussed below, can be straightforwardly extended to higher dimensions.
To find the proposed BCPWs, we first solve Eq. 3. By introducing an auxiliary variable 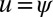 , the constrained optimization problem is equivalent to the following problem:
, the constrained optimization problem is equivalent to the following problem:
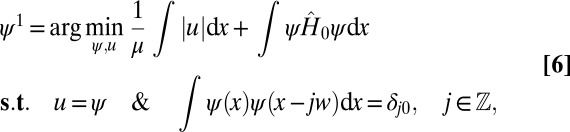 |
which can be solved by an algorithm based on the Bregman iteration (6–8).
Algorithm 1.
Initialize
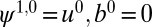 .
.
While “not converged” do
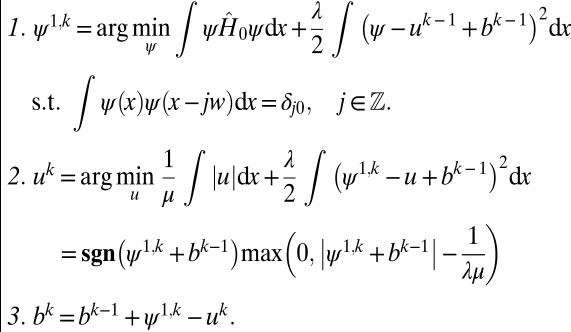 |
We solve the first problem in the above algorithm in the Fourier space, since the kinetic energy and the constraints are diagonal. In other words, let’s write 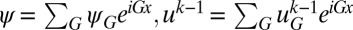 and
and 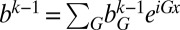 . Then we need to solve the following problem:
. Then we need to solve the following problem:
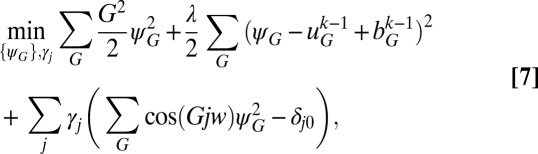 |
where 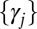 are Lagrangian multipliers associated with the orthonormality constraints, which can be found from the following nonlinear equations:
are Lagrangian multipliers associated with the orthonormality constraints, which can be found from the following nonlinear equations:
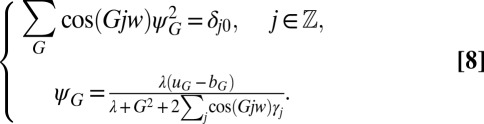 |
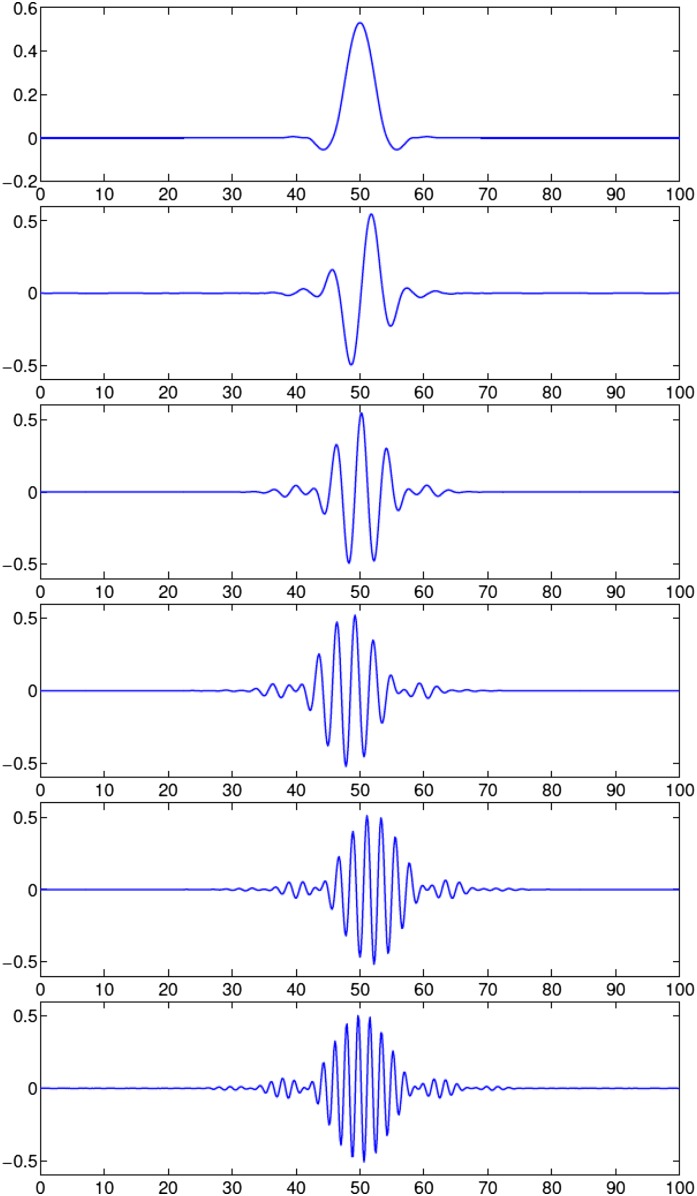
One can go further and define higher-order modes 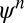 that satisfy Eqs. 3 and 4. The additional orthogonality constraints can be imposed using the method of splitting orthogonality constraint (SOC) proposed in ref. 9 and adopted in ref. 4 for calculating CMs. In Fig. 1, we illustrate the first six modes,
that satisfy Eqs. 3 and 4. The additional orthogonality constraints can be imposed using the method of splitting orthogonality constraint (SOC) proposed in ref. 9 and adopted in ref. 4 for calculating CMs. In Fig. 1, we illustrate the first six modes, 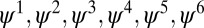 , obtained from Eqs. 3 and 4 using
, obtained from Eqs. 3 and 4 using 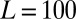 ,
, 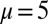 , and
, and 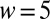 .
.
Fig. 1.
From top to the bottom, the first six modes, 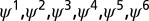 , obtained by Eqs. 3 and 4 using
, obtained by Eqs. 3 and 4 using 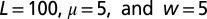 .
.
The next interesting property is the distribution of the spectral weight 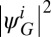 and the total spectral weight
and the total spectral weight 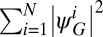 of the first six BCPWs, which are shown in Fig. 2. Fig. 2 Upper shows that each mode occupies a distinct region in the Fourier space. Moreover, the total spectral weight of the first six BCPWs forms a smoothed step function, which is a desirable property for obtaining convergence rates similar to the plane wave basis. In other words, locally, the basis covers approximately the same Fourier space as the plane wave basis below a given kinetic energy cutoff.
of the first six BCPWs, which are shown in Fig. 2. Fig. 2 Upper shows that each mode occupies a distinct region in the Fourier space. Moreover, the total spectral weight of the first six BCPWs forms a smoothed step function, which is a desirable property for obtaining convergence rates similar to the plane wave basis. In other words, locally, the basis covers approximately the same Fourier space as the plane wave basis below a given kinetic energy cutoff.
CPW Representations of Localized Functions
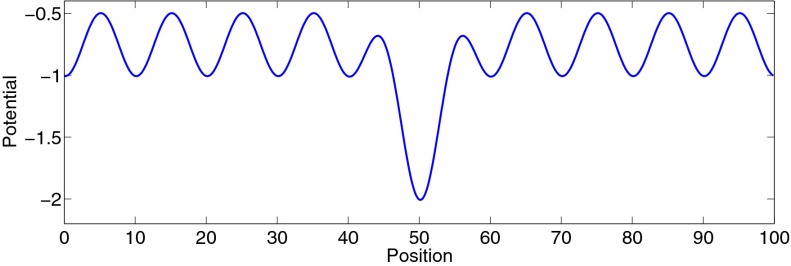
Localization properties of the proposed CPWs can be expected to bring advantages in applications where objective functions have rapidly varying fine structure in localized spatial regions. Taking an example from quantum mechanics, we will demonstrate the performance of CPWs for a 1D periodic potential where one of the potential wells is deeper than the others. This is analogous to introducing an “impurity” atom in a bulk solid, resulting in the potential function illustrated in Fig. 3; we call this an “impurity” Kronig-Penny (IKP) model. Using the first 120 CPWs generated by the first 6 BCPWs illustrated in Fig. 1, we would like to demonstrate several advantages of the CPW representation for this case, which combines both localized “impurity” modes and delocalized “bulk” modes.
Fig. 3.
The potential funciton 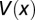 of the impurity Kronig-Penney model.
of the impurity Kronig-Penney model.
Choosing potential wells to be described by inverted Gaussians 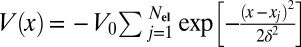 with
with 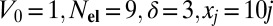 , and adding the central potential with
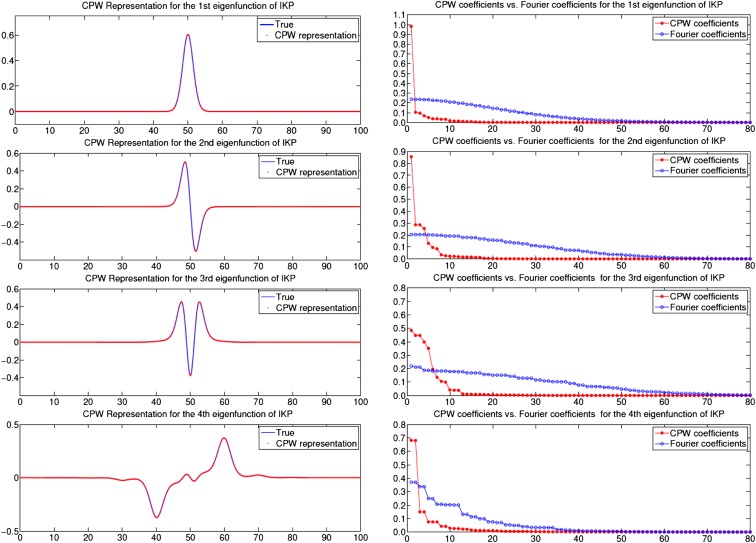
, and adding the central potential with 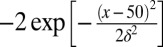 , the IKP model gives several localized impurity-like eigenstates. The blue curves in Fig. 4 Left show the wave functions of the four lowest-energy states of the IKP model. We can successfully recover these localized functions using the 6 BCPWs (corresponding to 120 CPWs after translations) generated in Numerical Algorithms for Constructing CPWs. Representation results plotted by red dots in Fig. 4 Left demonstrate the accuracy of the CPW expansion. In Fig. 4 Right, we compare the magnitude of the 80 largest CPW expansion coefficients with the classical Fourier plane wave coefficients for these wave functions. Fig. 4 clearly shows that CPWs can provide a much sparser representation of localized eigenfunctions than the plane wave basis. Table 1 gives a detailed comparison of the
, the IKP model gives several localized impurity-like eigenstates. The blue curves in Fig. 4 Left show the wave functions of the four lowest-energy states of the IKP model. We can successfully recover these localized functions using the 6 BCPWs (corresponding to 120 CPWs after translations) generated in Numerical Algorithms for Constructing CPWs. Representation results plotted by red dots in Fig. 4 Left demonstrate the accuracy of the CPW expansion. In Fig. 4 Right, we compare the magnitude of the 80 largest CPW expansion coefficients with the classical Fourier plane wave coefficients for these wave functions. Fig. 4 clearly shows that CPWs can provide a much sparser representation of localized eigenfunctions than the plane wave basis. Table 1 gives a detailed comparison of the 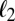 error of the CPW representation and plane wave representation using the first few largest magnitude coefficients. It is promising that, to achieve the same accuracy, the number of required CPWs is significantly smaller than the number of plane waves.
error of the CPW representation and plane wave representation using the first few largest magnitude coefficients. It is promising that, to achieve the same accuracy, the number of required CPWs is significantly smaller than the number of plane waves.
Fig. 4.
CPW representations for the first four energy states of IKP model. (Left) Comparisons of CPW representations for the first 4 eigenfunctions of the IKP model with their true values. (Right) Comparisons of the first 80 largest magnitude coefficients of CPW representations and classical Fourier function representations.
Table 1.
Comparisons of representation error using CPWs and Fourier basis
| No. of modes | Representation error using CPWs | Representation error using Fourier basis | ||||||
Error
|
Error
|
Error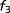
|
Error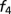
|
Error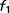
|
Error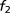
|
Error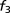
|
Error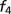
|
|
| 20 | 0.0091 | 0.0170 | 0.0305 | 0.0506 | 1.0282 | 1.3586 | 1.4886 | 0.4553 |
| 30 | 0.0051 | 0.0084 | 0.0111 | 0.0204 | 0.5052 | 0.8289 | 0.9951 | 0.2004 |
| 40 | 0.0038 | 0.0065 | 0.0076 | 0.0115 | 0.2112 | 0.4332 | 0.5875 | 0.0619 |
| 50 | 0.0036 | 0.0063 | 0.0066 | 0.0075 | 0.0763 | 0.1930 | 0.2964 | 0.0228 |
| 60 | 0.0035 | 0.0063 | 0.0064 | 0.0052 | 0.0242 | 0.0651 | 0.1304 | 0.0097 |
| 70 | 0.0035 | 0.0063 | 0.0064 | 0.0043 | 0.0068 | 0.0192 | 0.0470 | 0.0048 |
CPWs can also be used to successfully approximate the low-energy spectrum of the IKP model. In other words, we calculate eigenvalues of the matrix 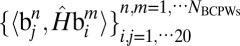 (
(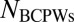 is the number of BPCWs) and compare those with the “exact” eigenvalues of the Schrödinger operator
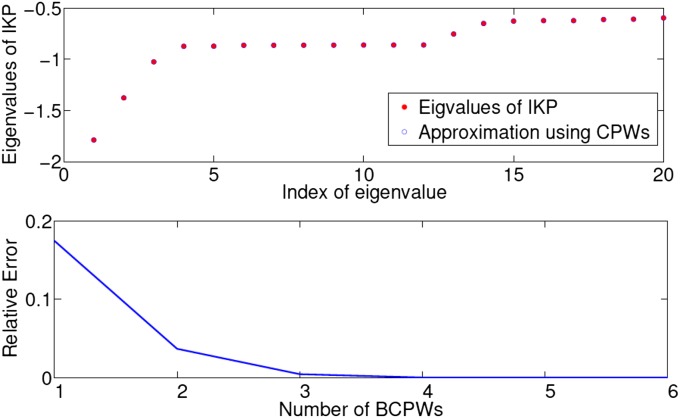
is the number of BPCWs) and compare those with the “exact” eigenvalues of the Schrödinger operator 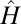 of the IKP model, calculated using a spectral method with 640 nodes. In Fig. 5 Upper, the red dots plot the lowest 20 “exact” eigenvalues of the IKP model, while the blue circles are approximation results using 120 CPWs. Fig. 5 Lower reports the corresponding relative approximation error as a function of the number of BCPWs used in the basis. It is clear that the truncated CPW expansion provides an accurate approximation for the low-energy eigenvalues of
of the IKP model, calculated using a spectral method with 640 nodes. In Fig. 5 Upper, the red dots plot the lowest 20 “exact” eigenvalues of the IKP model, while the blue circles are approximation results using 120 CPWs. Fig. 5 Lower reports the corresponding relative approximation error as a function of the number of BCPWs used in the basis. It is clear that the truncated CPW expansion provides an accurate approximation for the low-energy eigenvalues of 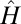 , i.e., the original eigenvalue problem can be reduced to an eigenvalue problem of a significantly smaller matrix.
, i.e., the original eigenvalue problem can be reduced to an eigenvalue problem of a significantly smaller matrix.
Fig. 5.
Eigenvalue approximation for the IKP model using the CPW representation. (Upper) The first 20 approximated eigenvalues using the first 120 CPWs vs. true values. (Lower) Relative eigenvalue approximation error using CPWs generated by the first 6 BCPWs.
The conclusion is that CPWs become attractive if one needs to represent a function that varies slowly (or is zero) through most of the space, except for a few regions; plane waves would need to increase the spatial resolution uniformly in the whole domain, while one can add CPWs locally in the regions of interest. Moreover, in Fast CPW Transforms, we show that CPW expansions can be efficiently processed using FFT-based CPW transforms.
Fast CPW Transforms
Given a function 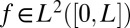 , we propose an algorithm to perform the transformation from f in real space to the basis coefficients
, we propose an algorithm to perform the transformation from f in real space to the basis coefficients 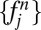 in frequency space. Recall that:
in frequency space. Recall that:
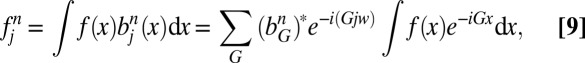 |
where 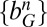 are the coefficients of
are the coefficients of 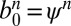 in the CPW expansion. In other words, we write
in the CPW expansion. In other words, we write 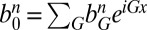 , and we have
, and we have
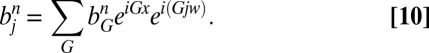 |
The computation of this transform can be performed efficiently in three steps as follows.
Algorithm 2 (Fast CPW Transform).
1. Fourier Transform.
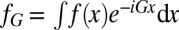 .
.
2. Multiplication and summation:
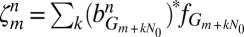 ,
, 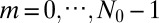 , where
, where 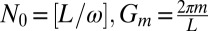 .
.
3. Fourier transforms of length
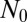 to get the basis coefficients:
to get the basis coefficients:
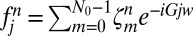 .
.
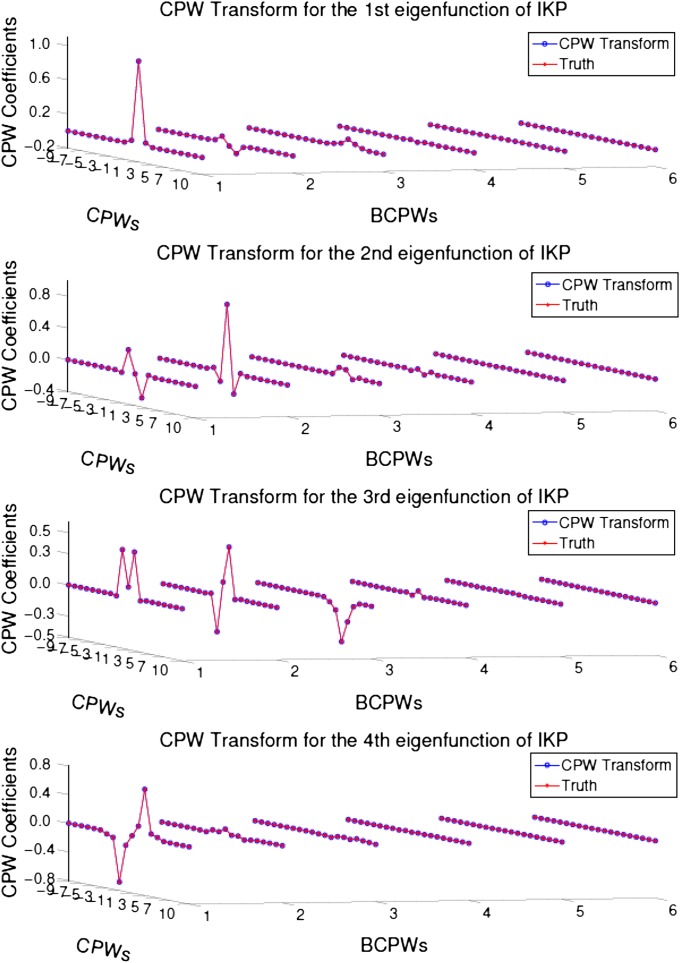
We demonstrate the fast CPW transform for the first four lowest-energy states of the IKP model. Fig. 6 illustrates the accuracy of the proposed algorithm for the CPW transform: The two sets of points are on top of each other (red dots and blue circles are obtained from direct diagonalization and fast CPW transform, respectively).
Fig. 6.
CPW transform for the first four lowest-energy states of the IKP model, where six levels of CPW transform are shown separately for each energy state.
Next, we propose an algorithm for the inverse transformation from given CPW coefficients 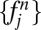 in frequency space to a function f in real space. We recall that:
in frequency space to a function f in real space. We recall that:
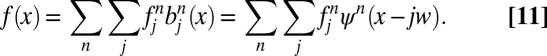 |
Therefore, one can rewrite f as
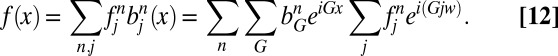 |
The above summation can be efficiently computed in the following three steps.
Algorithm 3 (Fast Inverse CPW Transform).
1. Fourier Transform.
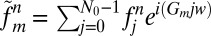 , where
, where
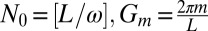 .
.
2. Multiplication and summation. Note that all
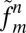 are periodic with a period
are periodic with a period
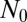 . Hence, we calculate
. Hence, we calculate
Here, we only need to go up to Fourier coefficient values m for which the corresponding basis function
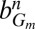 has nonzero coefficients. Then we add contributions from all n:
has nonzero coefficients. Then we add contributions from all n:
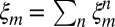 .
.
3. Fourier transform to real space
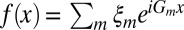 .
.
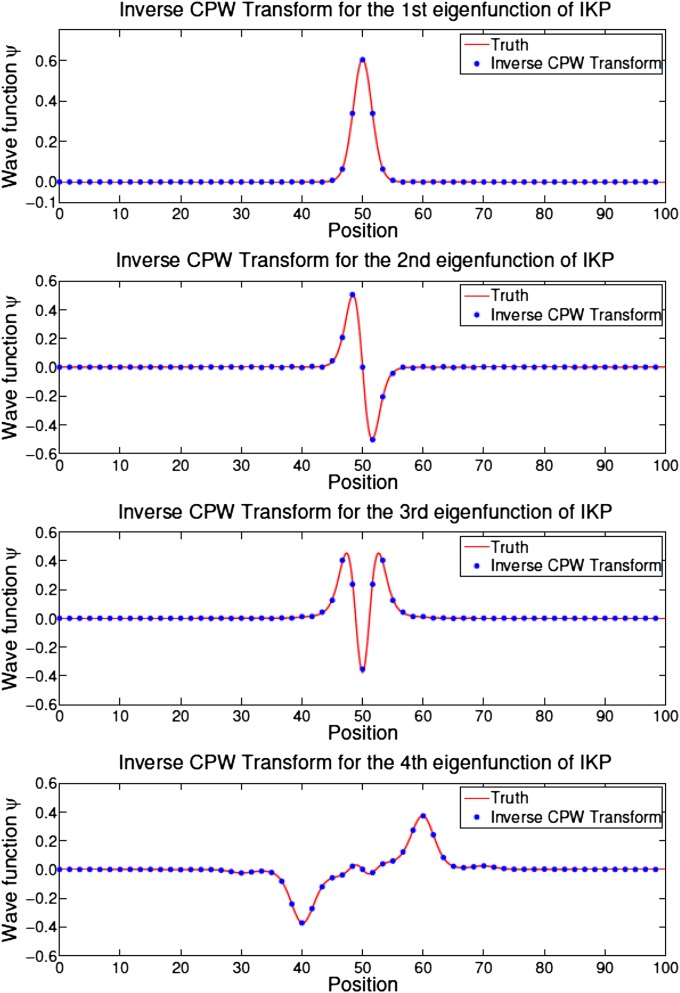
Using the first four lowest-energy states of the IKP model from Fig. 4 as an example, we test the inverse CPW transform based on the above algorithm; Fig. 7 shows the results, where the solid red line shows the “exact” results with a very fine mesh, while blue dots are obtained using the fast transform described above with a coarse mesh.
Fig. 7.
Reconstruction results using inverse CPW transform for the first four lowest-energy states of the IKP model.
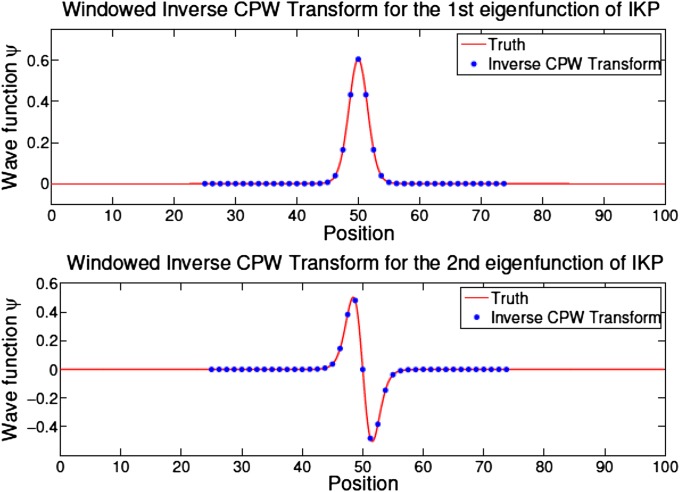
Furthermore, these transforms can be “windowed,” which allows the use of different meshes in different spatial regions, instead of having to use the same real-space mesh everywhere. We conduct numerical tests for the IKP model wave functions in Fig. 7, except that these transforms are carried out only over the region where these functions are nonzero. Fig. 8 reports the results obtained from the “windowed” inverse CPW transform, where the solid red line shows the “exact” results, while the blue dots are obtained using the “windowed” inverse CPW transform. Similarly, the CPW transform can also be windowed just like the “windowed” inverse CPW transform. These “windowed” transforms will be useful when one needs higher resolution only in certain limited regions.
Fig. 8.
Reconstruction results using windowed inverse CPW transform for the first two lowest-energy states of the IKP model.
Finally, the proposed model and numerical algorithms work on domains in higher-dimensional space. As an example, Fig. 9 shows computational results for the first BCPW of the Laplace operator on a 2D domain  with a square lattice
with a square lattice  . It is worth noting that our approach to obtaining CPWs in higher dimensions is essentially different from the usual method of obtaining a multidimensional basis by using a tensor product of 1D basis functions.
. It is worth noting that our approach to obtaining CPWs in higher dimensions is essentially different from the usual method of obtaining a multidimensional basis by using a tensor product of 1D basis functions.
Fig. 9.
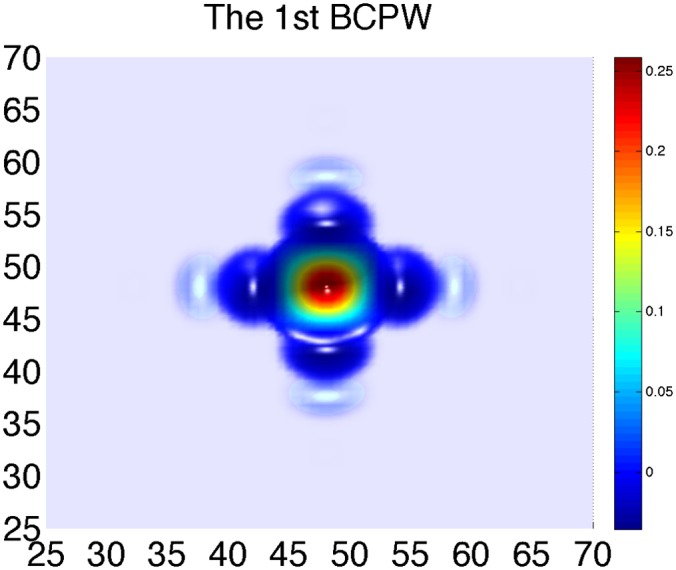
The first BCPWs in a 2D domain 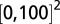 color-coded with its height functions, where we only show its nonzero part in domain
color-coded with its height functions, where we only show its nonzero part in domain 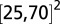 .
.
Discussion and Conclusions
We have presented an 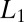 regularized variational method for producing CPWs, which constitute an orthonormal basis derived from the Laplace operator. CPWs form a natural set of modes with two parameters representing position and scale, as in wavelets, but, unlike wavelets, CPWs have their origin in a differential equation so that they may be used as a natural basis for solving PDEs and have a natural extension to higher dimensions. Numerical algorithms for solving the nonconvex optimization problem defining CPWs have been proposed. Numerical experiments show that CPWs can represent localized functions more efficiently than the plane wave basis, while maintaining similar performance as plane waves for spatially extended functions. Finally, fast transforms for transforming between the CPW coefficients and real-space mesh have been proposed. These algorithms can make use of highly efficient implementations of the FFT and can be “windowed” to perform FFTs only over those regions of real space where the function expansion is nonzero.
regularized variational method for producing CPWs, which constitute an orthonormal basis derived from the Laplace operator. CPWs form a natural set of modes with two parameters representing position and scale, as in wavelets, but, unlike wavelets, CPWs have their origin in a differential equation so that they may be used as a natural basis for solving PDEs and have a natural extension to higher dimensions. Numerical algorithms for solving the nonconvex optimization problem defining CPWs have been proposed. Numerical experiments show that CPWs can represent localized functions more efficiently than the plane wave basis, while maintaining similar performance as plane waves for spatially extended functions. Finally, fast transforms for transforming between the CPW coefficients and real-space mesh have been proposed. These algorithms can make use of highly efficient implementations of the FFT and can be “windowed” to perform FFTs only over those regions of real space where the function expansion is nonzero.
The CPW basis set proposed here addresses the need for multiresolution basis functions that can be defined for differential operators on general domains in 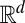 . In this sense, our work extends earlier work in this area, such as the diffusion wavelet proposed in ref. 10, which can be viewed as diffusion of delta functions where multiresolution is obtained by choosing different diffusion times. The method of ref. 10 is completely based on diffusion processing without considering any sparsity-inducing variational approach, and compact support emerges as a result of auxiliary constraint, while in our work, finite support is a natural consequence of a sparsity-inducing variational principle.
. In this sense, our work extends earlier work in this area, such as the diffusion wavelet proposed in ref. 10, which can be viewed as diffusion of delta functions where multiresolution is obtained by choosing different diffusion times. The method of ref. 10 is completely based on diffusion processing without considering any sparsity-inducing variational approach, and compact support emerges as a result of auxiliary constraint, while in our work, finite support is a natural consequence of a sparsity-inducing variational principle.
In the future, we expect to extend CPW techniques in a number of ways and adapt them to a variety of applications, such as: (i) constructing CPWs for more general elliptic operators, (ii) using CPWs as a representation for solving multiscale PDEs, and (iii) extending CPWs to higher dimensions and irregular domains. Finally, we plan to perform a theoretical analysis of CPWs to rigorously study their existence and properties, including the completeness that was hypothesized in this work.
Acknowledgments
V.O. acknowledges financial support from the National Science Foundation under Award DMR-1106024 and use of computing resources at the National Energy Research Scientific Computing Center, which is supported by the US Department of Energy (DOE) under Contract DE-AC02-05CH11231. The research of R.C. is partially supported by the US DOE under Contract DE-FG02-05ER25710. The research of S.O. was supported by the Office of Naval Research (Grant N00014-11-1-719).
Footnotes
The authors declare no conflict of interest.
References
- 1.Bracewell RN. The Fourier Transform and Its Applications. Vol 31999. New York: McGraw-Hill; 1986. [Google Scholar]
- 2.Oran Brigham E. The Fast Fourier Transform and Its Applications. Englewood Cliffs, NJ: Prentice Hall; 1988. [Google Scholar]
- 3.Daubechies I. Ten Lectures on Wavelets. Vol 61. Philadelphia: Society for Industrial and Applied Mathematics; 1992. [Google Scholar]
- 4.Ozoliņš V, Lai R, Caflisch R, Osher S. Compressed modes for variational problems in mathematics and physics. Proc Natl Acad Sci USA. 2013;110(46):18368–18373. doi: 10.1073/pnas.1318679110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Unser M, Thevenaz P, Aldroubi A. Shift-orthogonal wavelet bases. IEEE Trans Signal Process. 1998;46(7):1827–1836. [Google Scholar]
- 6.Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularization method for total variation-based image restoration. Multiscale Model Simul. 2005;4:460–489. [Google Scholar]
-
7.Yin W, Osher S, Goldfarb D, Darbon J. Bregman iterative algorithms for
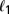 -minimization with applications to compressed sensing. SIAM J Imaging Sci. 2008;1(1):143–168. [Google Scholar]
-minimization with applications to compressed sensing. SIAM J Imaging Sci. 2008;1(1):143–168. [Google Scholar] -
8.Goldstein T, Osher S. The split Bregman method for
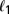 -regularized problems. SIAM J Imaging Sci. 2009;2(2):323–343. [Google Scholar]
-regularized problems. SIAM J Imaging Sci. 2009;2(2):323–343. [Google Scholar] - 9.Lai R, Osher S. A splitting method for orthogonality constrained problems. J Sci Comput. 2014;58(2):431–449. [Google Scholar]
- 10.Coifman R, Maggioni M. Diffusion wavelets. Appl Comput Harmon Anal. 2006;21(1):53–94. [Google Scholar]