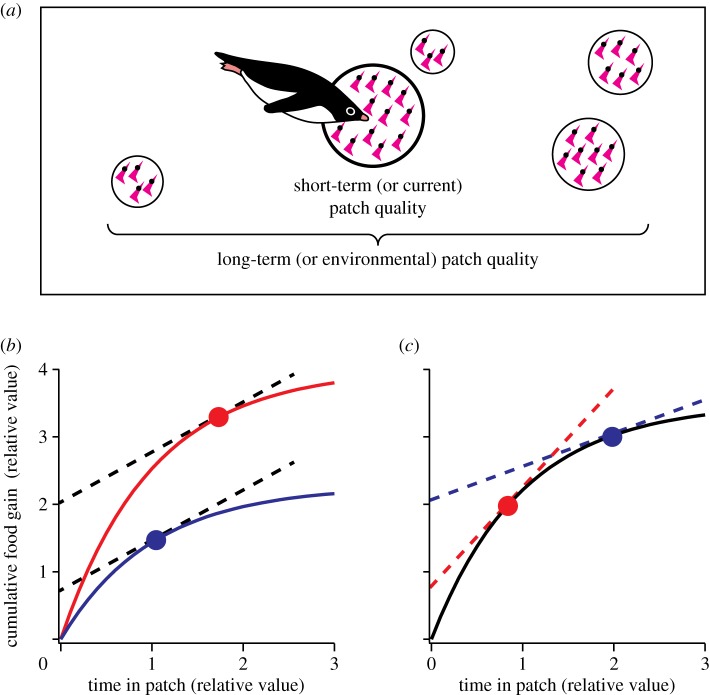
Figure 1.

Illustration and schematic diagram showing how optimal patch residence time will change in response to patch quality according to the MVT. (a) Consider an animal foraging in an environment where prey patches are heterogeneously distributed. The theorem states that animals should leave a patch when the instantaneous food gain rate in the patch (the gradient of gain function curves in (b,c)) drops to the long-term food gain rate across many patches in the environment (the slope of dotted lines in (b,c)). Two main predictions arise from the theorem. (b) Consider two patches in which short-term quality varies (high, red curve; low, blue curve) but long-term quality is constant (dashed line). In this case, animals are predicted to stay longer in the patch with higher short-term quality. (c) Consider two patches in which short-term quality is constant (solid curve) but long-term quality varies (high, red dashed line; low, blue dashed line). In this case, animals are predicted to stay more briefly in the patch with higher long-term quality. In dynamic patch systems such as krill swarms, both short- and long-term patch quality are rarely constant, and what we would expect to observe in the penguin–krill system is a combination of (b) and (c).