The direct and indirect impact of comorbidity on the survival of patients with non-small cell lung cancer: a combination of survival, staging and resection models with missing measurements in covariates

Abstract

Objective

To examine the direct and indirect impact of comorbidity on the survival.

Design

A historical cohort study.

Setting

Denmark.

Participants

All patients with non-small cell lung cancer who were registered in the Danish Lung Cancer Registry in 2010.

Main outcome measures

The influence of comorbidity on stage misclassification, probability of resection and survival.

Results

It was estimated that the comorbidity influences the probability of resection with OR 0.65 and 95% credible interval (0.54; 0.79), the staging process with OR 1.08 and 95% credible interval (0.96; 1.20), and the survival process with HR 1.08 and 95% credible interval (1.02; 1.14).

Conclusions

We found that comorbidity has a significant indirect effect on survival mediated by the resection process and a slightly direct effect on mortality.

Strengths and limitations of this study.

• The strength of this study is that it is a population-based study.

• In this study, we used Charlson comorbidity index with only hospital diagnoses. It is, thus, possible that some patients with comorbid conditions may have been misclassified as having no comorbidity.

Introduction

Primary lung cancer is one of the most common cancers in Denmark with more than 4000 new cases/year. The prognosis for patients with lung cancer is poor with crude 5-year survival proportions of approximately 10–12%. However, there is evidence of some improvement in patient mortality in most recent years.¹ Approximately 90% of lung cancers have been attributed to cigarette smoking,^{2 3} with age as an additional risk factor. Furthermore, age^{4 5} and smoking^{6 7} are strongly associated with comorbidity, that is, diseases and conditions coexisting with lung cancer.⁸ As our society ages, clinicians will encounter older patients more frequently and with increasing probability that patients with lung cancer will have coexisting diseases. It is well established that comorbidity has an effect on survival.^{9 10}

However, comorbidity may influence survival in different ways. First, patients with lung cancer frequently present with other diseases, including chronic obstructive lung disease, cerebrovascular diseases, heart failure and myocardial infarction. Such types of comorbidity may by itself have a negative effect on survival. Second, comorbidity may significantly mask symptoms and delay the establishment of the diagnosis of lung cancer or even prevent a full diagnostic evaluation with proper staging of the disease. Third, surgical intervention has a positive effect on the survival of lung cancer,¹¹ but comorbidity may contradict surgical intervention in patients otherwise eligible for surgery. “Mostly, comorbidities will have a negative impact on survival, but it can increase the person's contact with the medical practitioners as it may indirectly have a positive impact on survival by increasing the likelihood of earlier diagnosis.”

Simultaneous estimation of models describing a diagnostic process, surgical intervention, along with the survival process, makes more efficient use of available data and make it possible to estimate the influence of comorbidity with respect to diagnostic procedures, treatment options and the prognosis in patients with lung cancer in a situation with partially missing data. Since non-small cell lung cancer (NSCLC) and small cell lung cancer (SCLC) differ in the sense of clinical characteristics, treatment options and survival, this study was restricted to patients with NSCLC.

Methods

Patient population and clinical data

The Danish Lung Cancer Registry

Since the establishment in 2000, the Danish Lung Cancer Registry (DLCR) has accumulated data on all cases of lung cancer as reported from about 50 departments involved in the care of primary lung cancer in Denmark.¹² Data are reported to the database when the diagnostic evaluation has been completed, and when a specific treatment has been finished. This registry information is then supplemented with data on the patient's vital status retrieved from the Danish Civil Registration System, and pathology information related to the lung cancer case from the Danish Pathology Register.

Diagnostic evaluation and treatment options

Diagnostic procedures in suspected lung cancer are primarily performed to establish that the presence of disease and the type and clinical staging of lung cancer. Lung cancer is divided into two main types based on histology, SCLC (10–15%), and NSCLC (85–90%). When the type of lung cancer is established, further investigations are performed to evaluate whether the patient is eligible for treatment, and if so, what kind of treatment. Patients with lung cancer with NSCLC are, in principle, treated with surgical resection or chemotherapy and/or radiotherapy. Surgical resection of the tumour is associated with the most favourable survival rates, but only 20% of the patients are eligible for resection at the time of diagnosis. The clinical stage is the most important factor when deciding the choice of treatment. However, the true stage is only identifiable in connection with surgery. The risk of misclassification depends on how advanced the disease is at the time of diagnosis. Since it is relatively easy to stage a patient with an advanced disease (large tumour involving other organs and/or metastasis corresponding to clinical stage IIIb or IV), the risk of misclassification is of minor importance in an advanced disease. On the other hand, misclassification is more common in a local disease, where it can be difficult to distinguish between the denominators defining the different subcategories of clinical stages I–IIIa. Since the choice of treatment, to a great extent, depends on the clinical stage, misclassification in a local disease does affect the type of treatment offered to the patient. Furthermore, a range of other prognostic factors are also taken into account before the final decision about treatment is made, including age, alcohol or drug missuse and comorbidity.

Comorbidity

We included information on comorbidity for each patient up to 10 years before the lung cancer diagnosis, using the Danish National Patient Register, which was established in 1977. This register contains data including coding of all interventions related to diagnostic evaluation and treatment for all somatic patient admissions in Denmark.¹³ For the classification of comorbidity, we used a slight modification of the Charlson comorbidity index (CCI)¹⁴ by excluding all interventions with lung cancer as the activity diagnosis and registered prior to the date of diagnosis for the present patient group (see below). This was carried out in order to avoid the contribution to the CCI from the very few patients who had a previously registered course of lung cancer in the Danish National Patient Register. Relevant diseases are grouped into a total of 19 categories, each of which assigned a score between 0 and 6 depending on assumed severity. The CCI is calculated as the sum across these categories and will range between 0 (with no diseases in the medical history qualifying for inclusion in the CCI) and 37 (a medical history representing all diseases of the highest severity, qualifying for inclusion in the CCI). As the Danish National Patient Register covers all somatic activities, all patients are identifiable without exceptions. Thygesen et al¹⁵ showed that the predictive value of using the coding practice in the register to establish the CCI is consistently high. Any hospital contact represented with a cancer diagnosis registered within 150 days before the date of lung cancer diagnosis was excluded from contribution to the CCI. This was carried out to avoid the influence of misclassification by cases with a cancer diagnosis (including cancers of neighbouring organs) that eventually turned out to be verified as lung cancer. Based on a sensitivity analysis, only very few, if any, cancer of other organs than the lungs will be missed by this procedure. Patients with lung cancer were, thereafter, grouped according to the increased level of CCI as follows: (1) persons with a CCI score of 0; (2) persons with a CCI score of 1–2 and (3) persons with a CCI score of 3+.

Study population

We have chosen to base our analysis on a subset of DLCR, which consists of all 3135 patients with NSCLC who were registered in 2010. We have the information on age, sex, clinical stage, resection status and district on 2840 of those patients. The DLCR is described in detail in ref. 12.

The detailed distribution of CCI in the patient sample can be seen in figure 1. The proportions of patients in three comorbidity groups are 46.4%, 38.1% and 15.5%.

Figure 1.

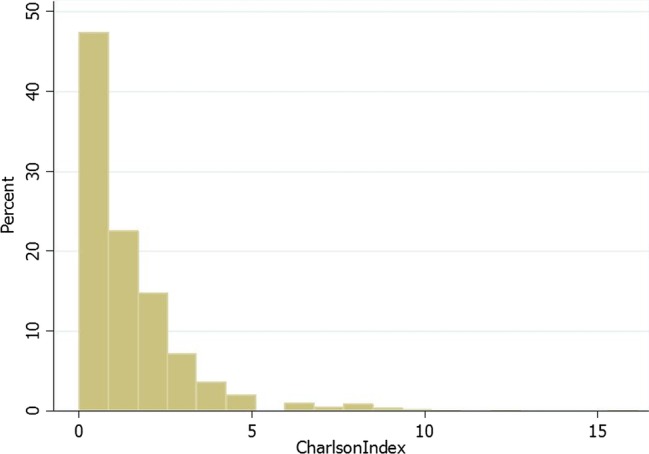
Distribution of Charlson comorbidity index in the study population.

Table 1 shows the relationship between clinical and surgical stages. Only 16% of the patients have a surgical stage registered. In this subset, the clinical and surgical stages are identical for 430 (68%) patients, while in 127 (20%) of the patients the clinical stages are classified as lower than the surgical stage and in 73 (12%) of the patients the clinical stages are rated higher than the surgical stage.

Table 1.

Distribution between clinical and surgical stages in the study population

Clinical stages	Surgical stages					No data (no surgery)	Total
	0,I	II	IIIa	IIIb	IV
0,I	280	56	28	0	4	187	555
II	39	98	33	1	5	153	329
IIIa	8	16	33	1	0	374	431
IIIb	0	1	0	1	0	371	373
IV	3	2	1	0	13	1489	1508
Total	330	173	95	3	22	2573	3196

Model formulation

For each individual, we observe survival data and covariate data. We assume the survival data to be subject to right censoring. For each individual, there are fully or partially observed vector of confoundings consisting of age, sex, comorbidity, clinical stage, surgical stage and resection status. There are five districts in Denmark in total. Recently, heterogeneity across Danish districts in the survival of patients with lung cancer has been demonstrated.¹⁶ This heterogeneity cannot be ignored, and thus districts will be treated as dummy variables in the models (see figure 2).

Figure 2.

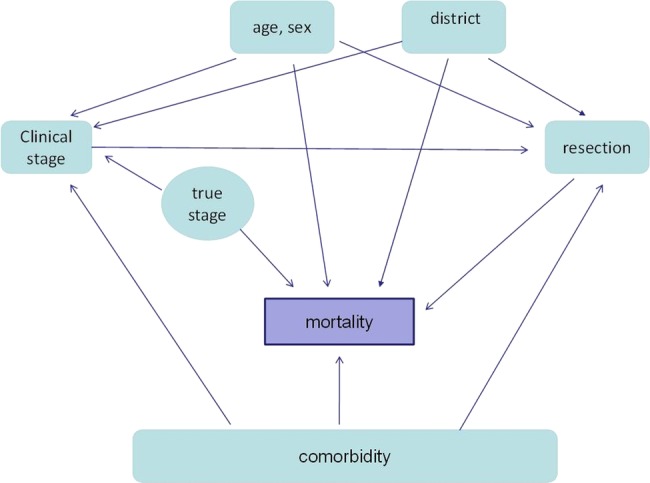
Graphical representation of the model.

Our proposed method consists of three models. The first one describes the likelihood model for the resection status in the form of a logistic regression adjusted for age, sex, comorbidity and clinical stage. We hereafter refer to this model as the ‘resection model’.

The second model describes the likelihood model for the surgical stage in the form of an ordinal logistic regression adjusted for age, sex, comorbidity and true stage. We hereafter refer to this model as the ‘staging model’.

The last model is a survival model. Here we estimate the hazard of failure through the proportional Cox regression model,¹⁷ where the hazard depends on the covariate through its current value adjusting for age, sex, comorbidity, resection status and true stage. We hereafter refer to this model as the ‘survival model’. Here we used a sandwich estimator derived by Lin and Wei.¹⁸ Lin and Wei show that the estimate is consistent and robust to several possible misspecifications in the Cox model including the lack of proportional hazard and incorrect functional form for the covariates.

To estimate the direct and indirect effect of comorbidity on survival, these three models must be estimated jointly in one simultaneous procedure.

Assumptions

Surgery provides for the optimal possibility of correct disease staging of the patient. Therefore, in our notation, the true stage is equal to the surgical stage.

As aforementioned, the true stage is observed only for the patients who have had surgery, which is less than 20% of all patients. In this study, we assume that the classification process for patients without surgery is identical with that for patients with surgery, that is, the missing data process for observing ‘true stage’ is missing at random. Using this assumption, we can handle the missing data problem using one of the common techniques for this purpose: multiple imputation.

Framework for multiple imputation

Generally, there are three mechanisms behind missing data:¹⁹ data can be ‘Missing Completely at Random’ (MCAR), ‘Missing at Random’, (MAR) and data can be missing in an unmeasured fashion ‘Missing Not at Random’ (MNAR). See refs. ²⁰ and ²¹ for review of important statistical methods for missing data.

We assume the missing data in our sample to be MAR.

Imputation and weighting^{22 23} are two important approaches in dealing with MAR missing data problems. Wang and coauthors² show that in many situations, some inverse selection probability-weighted estimators are numerically equivalent to imputation. The performance of multiple imputation has been well studied and it has been shown to perform favourably.^25–27 If MAR holds, it has been shown that multiple imputation produces unbiased parameter estimates which reflect the uncertainty associated with estimating missing data. Moreover, multiple imputation has been shown to be robust to departures from normality assumptions.²⁸

There are many different ways to impute values, constructing a complete dataset. In this work, we use the stochastic regression imputation. Missing values were replaced by predicted values from a regression model-contained covariates: age, sex, comorbidity and clinical stage plus residuals, drawn to reflect uncertainty in the predicted values.

According to King et al,²⁹ about 5 or 10 imputed datasets are often satisfactory. In Bayesian simulation, the distribution of variables in missing data process simulated jointly as well as parameters in a regression equation, that is, in WinBugs³⁰ (estimation platform for Bayesian simulations), the programme is going to treat all of the missing elements of the data as if they were unknown model parameters.

Results

Table 2 shows the descriptive characteristics of the study population.

Table 2.

Descriptive characteristics of the study population

	N (%)
Age
<67)	1209 (42.6)
≥67	1631 (57.4)
Sex
Male	1467 (51.6)
Female	1373 (48.4)
Operation
Yes	540 (19)
No	2300 (81)
CCI
0	1318 (46.4)
1	1082 (38.1)
>1	440 (15.5)

Table 3 shows the estimated effect of comorbidity and other adjusting parameters. First, consider the results for the resection model. The model shows that the increasing level of comorbidity significantly reduces the probability of resection. Models also show that increasing age reduces the probability of resection; sex has no statistically significant effect on the probability of resection; a high clinical stage reduces the probability of resection substantially.

Table 3.

Estimating results of the combination of models based on 2000 Monte Carlo dataset simulations reported by HR with 95% credible interval for the Cox regression (Survival model) and OR with 95% credible interval for the logistic regression (resection model) and for the ordered logistic regression (classification model)

Model	Parameter	HR/OR (2.5%; 97.5%)
Resection	Age (≥67 vs <67)	0.47 (0.36; 0.63)
	Sex (female vs male)	1.01 (0.79; 1.35)
	Comorbidity (growing)	0.65 (0.54; 0.79)
	Clinical stage (growing)	0.19 (0.16; 0.21)
Classification	Age (≥67vs <67)	0.53 (0.47; 0.66)
	Sex (female vs male)	1.23 (1.08; 1.49)
	Comorbidity (growing)	1.08 (0.96; 1.20)
	True stage (growing)	0.41 (0.38; 0.45)
Survival	Age (≥67 vs <67)	1.30 (1.16; 1.40)
	Sex (female vs male)	0.87 (0.78; 0.93)
	Comorbidity (growing)	1.08 (1.02; 1.14)
	Resection status (yes vs no)	0.17 (0.15; 0.21)
	True stage (growing)	0.13 (0.08; 0.16)

The staging model is most influenced by the missing data process and the staging model shows, as expected, that the true stage is negatively correlated with the clinical stage. The model also indicates that age and sex have an influence on the staging process. Moreover, it shows that increasing comorbidity has a slight, but not significant, effect on the staging process.

The survival model shows that increased comorbidity increases the mortality significantly. Increased age and advanced clinical stage are associated with the significantly increased mortality. Women have a significantly better survival compared with men. Resection is associated with a substantial reduction in mortality.

In addition, we performed an analysis with an alternative assumption about the missing data process, namely, that there is no misclassification of stages for patients without surgery. In that case, the measurement of clinical stage was used in models (2) and (3) instead of true stage, for the patients without surgery. The results of both analyses are very similar with respect to direct and indirect effects of comorbidity on survival.

Discussion

In this paper, we used an estimation method that allows a combination of different models in order to estimate the direct and indirect impact of comorbidity on survival in a situation with partially incomplete data.

In our study, the missing data problem concerns the lack of information on the true stage in patients who have not had surgery. We manage this problem by applying assumptions that represent two clinically extreme scenarios, ‘no misclassification at all for patients without resection’ and ‘misclassification at random’. We cannot be certain which scenario is closer to the reality, but clinical experience suggests that the real misclassification process for the patients, who were not operated, is somewhere in between these two scenarios. In clinical practice, it is well known that treatment with the intention of cure, such as resection, requires precise pretreatment patient evaluation including valid clinical staging. Owing to this, it is plausible that misclassification in this group of patients is smaller than in patients selected for a palliative treatment. On the other hand, it is often easier and faster to come to a diagnostic conclusion in patients with advanced disease, and decisions about treatment are, therefore, made before all investigations are finished, thus making the staging more uncertain. Despite the fact that we used two clinically opposite assumptions about the missing data process, the direct effect of comorbidity on the estimated survival, using both approaches, is substantially equal. This may be because our model is quite stable, but could also be explained by bias in both estimates. Further work is needed to clarify this.

In this study, the variable resection was treated as known at baseline. We are aware that it potentially could be a source of bias. We believe that this bias is disparaged to be small, and therefore could be ignored. As all the information needed to decide about resection is presented at the baseline and mortality in the group of potentially inoperable patients is very small, in the period from baseline (day of diagnose) to operation day.

From a clinical point of view, our results seem plausible. The estimated effects of age, sex, stage and resection are generally as expected concerning the probability of resection, staging and survival. It appears that the direct and indirect effects of comorbidity in general are as expected.

In this study, we used CCI with only hospital diagnosis of diseases as a measure of comorbidity. It is, thus, possible that some patients with comorbid conditions may have been misclassified as having no comorbidity. It will be relevant to perform the same analysis using CCI based on diagnoses from general practice; unfortunately, these data are not available yet. In the future work, we will investigate the prognostic effect of the individual diseases contributing to the overall CCI on the survival of patients with lung cancer.

We conclude that our work represents a useful solution to the statistical management of the complex influence of comorbidity on survival under incomplete data. We have used NSCLC, but the approach seems applicable to other diseases with similar complexity. The proposed approach can be easily generated to other applications.

Conclusion

We found that comorbidity has a significant indirect effect on survival of NSCLC patients mediated by the resection process, and a slightly direct effect on mortality. Further research is needed to compare the performance of the CCI to other comorbidity indices.