Figure 1. Procedures for estimating MI.
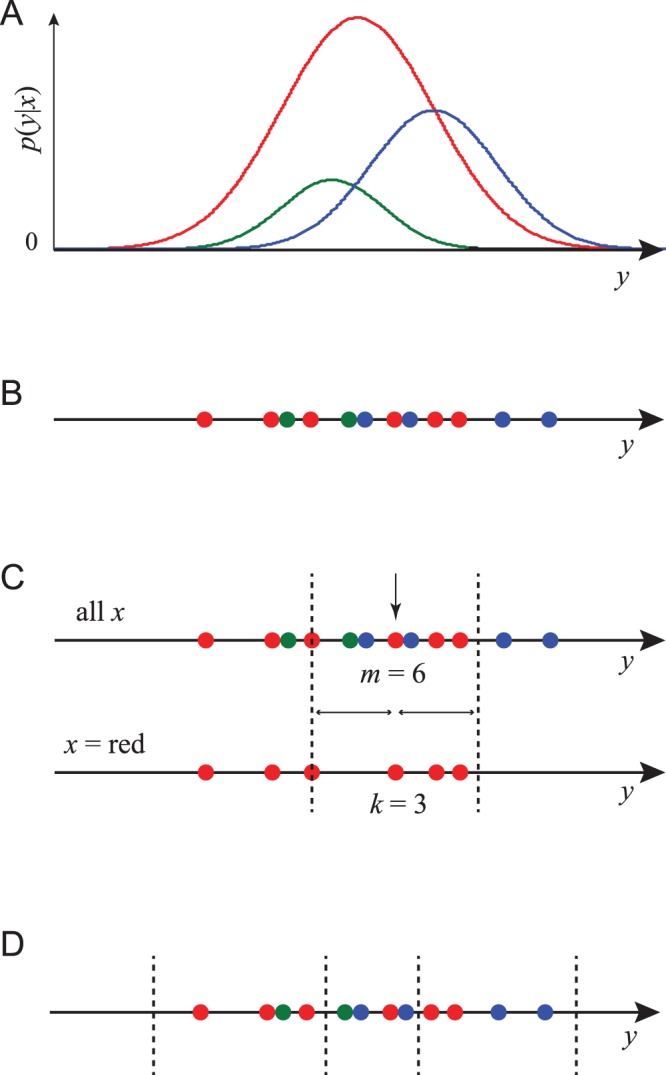
(A) An example joint probability density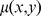 
where 
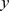is a real-valued scalar and 
can take one of three values, indicated red, blue and green. For each value of 
the probability density in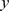 
is shown as plot of that color, whose area is proportional to 
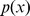. (B) A set of 
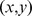data pairs sampled from this distribution, where 
is represented by the color of each point and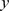 
by its position on the 
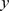-axis. (C) The computation of 
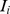in our nearest-neighbor method. Data point 
is the red dot indicated by a vertical arrow. The full data set is on the upper line, and the subset of all red data points is on the lower line. We find that the data point which is the 3rd-closest neighbor to 
on the bottom line is the 6th-closest neighbor on the top line. Dashed lines show the distance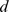 
from point 
out to the 3rd neighbor.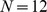 
, 
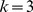, and for this point 
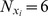and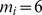 
. (D) A binning of the data into equal bins containing 
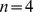data points. MI can be estimated from the numbers of points of each color in each bin.