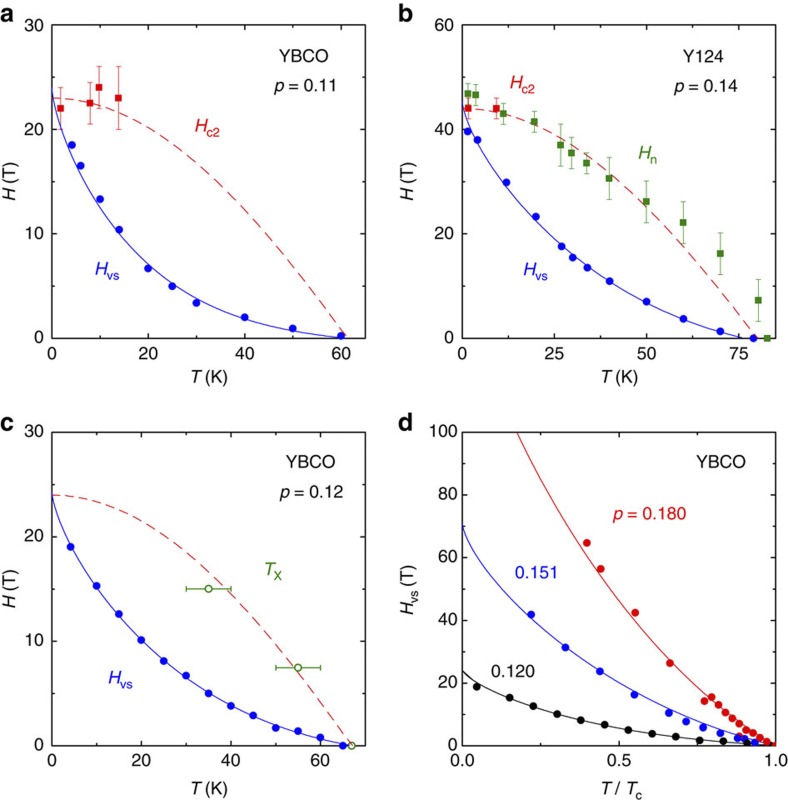
Figure 3. Field-temperature phase diagram of YBCO and Y124.

(a,b) Temperature dependence of H_c2 (red squares, from data as in Fig. 1) for YBCO and Y124, respectively. The red dashed line is a guide to the eye, showing how H_c2(T) might extrapolate to zero at T_c. Error bars on the H_c2 data represent the uncertainty in locating the onset of the downward deviation in κ vs H relative to the normal-state behaviour. The solid lines are a fit of the H_vs(T) data (solid circles) to the theory of vortex-lattice melting1, as in ref. 14. Note that H_c2(T) and H_vs(T) converge at T=0, in both materials, so that measurements of H_vs vs T can be used to determine H_c2(0). In Fig. 3b, we plot the field H_n defined in Fig. 1f (open green squares, from data in ref. 11), which corresponds roughly to the upper boundary of the vortex-liquid phase (see Supplementary Note 3). Error bars on the H_n data represent the uncertainty in locating the onset of the downward deviation in ρ vs H relative to the normal-state behaviour. We see that H_n(T) is consistent with H_c2(T). (c) Temperature T_X below which charge order is suppressed by the onset of superconductivity in YBCO at p=0.12, as detected by X-ray diffraction24 (open green circles, from Supplementary Fig. 7). Error bars on the T_X data represent the uncertainty in locating the onset of the downward deviation in the x-ray intensity vs T at a given field relative to the data at 17 T (see Supplementary Fig. 7a). We see that T_X(H) follows a curve (red dashed line) that is consistent with H_n(T) (at p=0.14; Fig. 3b) and with the H_c2(T) detected by thermal conductivity at lower temperature (at p=0.11 and 0.14). (d) H_vs(T) vs T/T_c, showing a marked increase in H_vs(0) as p goes from 0.12 to 0.18. From these and other data (in Supplementary Fig. 6), we obtain the H_vs(T→0) values that produce the H_c2 vs p curve plotted in Fig. 4a.