Abstract
In a typical case-control study, exposure information is collected at a single time-point for the cases and controls. However, case-control studies are often embedded in existing cohort studies containing a wealth of longitudinal exposure history on the participants. Recent medical studies have indicated that incorporating past exposure history, or a constructed summary measure of cumulative exposure derived from the past exposure history, when available, may lead to more precise and clinically meaningful estimates of the disease risk. In this paper, we propose a flexible Bayesian semiparametric approach to model the longitudinal exposure profiles of the cases and controls and then use measures of cumulative exposure based on a weighted integral of this trajectory in the final disease risk model. The estimation is done via a joint likelihood. In the construction of the cumulative exposure summary, we introduce an influence function, a smooth function of time to characterize the association pattern of the exposure profile on the disease status with different time windows potentially having differential influence/weights. This enables us to analyze how the present disease status of a subject is influenced by his/her past exposure history conditional on the current ones. The joint likelihood formulation allows us to properly account for uncertainties associated with both stages of the estimation process in an integrated manner. Analysis is carried out in a hierarchical Bayesian framework using Reversible jump Markov chain Monte Carlo (RJMCMC) algorithms. The proposed methodology is motivated by, and applied to a case-control study of prostate cancer where longitudinal biomarker information is available for the cases and controls.
Keywords: Adaptive knot selection, Exposure trajectory, Influence function, Odds ratio, Regression spline, Risk score diagnostics, Semiparametric modeling
1 Introduction
In a typical case-control study, subjects are sampled conditional on disease status and then exposure history is retrospectively retrieved and assessed. Case-control studies are often embedded in large cohorts where repeated/single measures on past exposure information can be obtained for all the study subjects, and thus for the selected case-control sample. Many cohort studies store serum, tissue and other bio-specimen samples for all enrolled subjects and a case-control design can be used to assay selected case-control samples instead of assaying the entire cohort. This retrospective design thus leads to cost and resource saving when expensive assays are not feasible for a large cohort (Ernster, 1994; Breslow, 1996). In particular, we consider the setting of a large cohort study where repeated measures on biological samples (like blood) have been archived for all study subjects. A case-control design is then employed to select samples for which a biomarker or a potential risk factor will be assayed/measured, after the study period is over. Thus case-control status is determined at the conclusion of the follow-up period. The scientific/statistical question is whether we can/should use all of the past measures and assay all available archived samples for selected cases and controls to infer about disease risk. Thus our goal is to construct measures of cumulative exposure to characterize disease-exposure association using available longitudinal exposure data (Thomas, 1983, 1988) and to provide odds ratios that are able to compare different types of exposure time-trajectories.
Some recent medical studies have indicated that incorporating the entire exposure history, when available, may lead to more precise and clinically meaningful estimation of disease risk. For example, Lewis et al (1996) report that by integrating the lifetime history of oral contraceptive (OC) use, they obtain scientifically more plausible inference on the odds ratio corresponding to the use of OC for risk of venous thromboembolism than that provided by measuring current use of OC in a matched case-control study. Such an analysis may also provide insight on how the present disease status of a subject is being influenced by past exposure conditional on the current exposure. In this paper, we present a Bayesian semiparametric approach for utilizing past longitudinal exposure history in case-control studies. The Bayesian joint model we propose estimates the time-varying exposure trajectories as well as the function that captures their influence on disease risk (which we call the influence function) in a flexible non-parametric way. The cumulative exposure effect is then aggregated over time, by integrating the exposure trajectory weighted by the influence function over a given time interval. We are then able to compare the odds of disease corresponding to different shapes of exposure profiles as well as the relative contribution of different time windows using the disease risk model.
Statistical analysis of case-control data was pioneered by Cornfield (1951, 1961) and Mantel and Haenszel (1959) and many important contributions followed over the next half century (Breslow et al, 1978; Prentice and Pyke, 1979; Zelen and Parker, 1986; Seaman and Richardson, 2001, 2004, to name a few). However, rigorous statistical methods for incorporating longitudinally varying exposure information under case-control sampling have not yet been adequately developed. Moulton and Monique (1991) consider a similar problem with time varying binary/categorical exposure and carry out a time-stratified analysis, then combine the regression coefficients across time to create time-specific summary quantities of interest. Park and Kim (2004) consider a serial case-control study where subjects could be cases at one predetermined sampling time and controls at another sampling window, leading to time-varying case-control status and exposure information. They illustrate that a naive generalized estimating equation (GEE) approach with compound symmetry correlation structure, that is commonly used under a prospective design does not work under case-control sampling design. Freedman et al (2009) incorporate smoking history as a time-varying exposure in a case-control study using a survival analysis framework.
In the present paper we do not treat the exposure trajectories as a time varying exposure in our final disease risk model, but create a cumulative measure that reflects the varying contribution of the different time intervals through the influence function. In analyzing the effect of a longitudinally varying exposure profile on a binary outcome variable (like disease status), some of the well-recognized challenges are: (1) The longitudinal exposure observations may be unbalanced in nature, i.e., the number of observations and also the observation times may differ from subject to subject; (2) The exposure trajectory may be highly nonlinear; (3) The exposure observations may be subject to considerable measurement error and (4) The effect of the exposure profile on the disease outcome may itself be complex and can even change over time. In view of the above challenges, we propose to use functional data analytic techniques, specially nonparametric regression methodology to model both the time varying exposure profile and also the influence pattern of the exposure profile on the binary outcome to account for any smooth time varying patterns of influence. Specifically, we model the underlying exposure trajectory and the effect pattern of the exposures on the current disease state using free knot regression splines (Lindstrom, 1999; DiMatteo et al). We have implemented a fully data-driven, adaptive knot selection scheme that identifies the optimal number and location of the knots in both the trajectory and influence functions via Reversible jump MCMC (RJMCMC) algorithms (Green, 1995; Botts and Daniels, 2008). Analysis is carried out in a hierarchical Bayesian framework. Our modeling framework can accommodate any possible non-linear time varying pattern in the exposure and influence profiles, and thus offers additional flexibility over a fully parametric formulation. Moreover, the joint Bayesian model ensures proper propagation of uncertainty via an integrated computational scheme. An additional aspect of our paper is to carry out model checking and assessment using various functions of the risk scores that we define in Section 5.
Remark 1: A natural question that may arise in this context is the issue of prospective and retrospective equivalence under such a framework. We show that the equivalence results of Seaman and Richardson (2004) applies to the proposed semiparametric framework thus enabling us to perform the analysis based on a prospective likelihood even though a case control study is retrospective in nature.
The remaining sections are organized as follows. In Section 2, we describe the Beta Carotene Retinol Efficacy trial and the related prostate cancer dataset which motivated our study. In Section 3, we introduce the details of our semiparametric modelling approach. Section 4 describes posterior inference and introduces the adaptive knot selection scheme. Section 5 outlines the model comparison and assessment procedures. We describe the data analysis results based on the prostate cancer data set in Section 6 and end with a discussion in Section 7. Details regarding the adaptive knot selection algorithms and the Bayesian equivalence results are included in the supplementary materials(web appendix).
2 Example: Prostate Cancer Study from the CARET Trial
We illustrate our methodology using a dataset from the Beta Carotene and Retinol Efficacy Trial (CARET), a randomized trial conducted by the Fred Hutchinson Cancer Research Center. The current dataset is designed to study the association between prostate cancer and prostate-specific antigen (PSA) and has previously been used to assess the predictiveness of PSA as a biomarker-based screening procedure for prostate cancer (Etzioni et al, 1999).
Participants in this study included men aged 50 to 65 at high risk of lung cancer. They were randomized to receive either placebo or Beta Carotene and Retinol. From the initial CARET cohort of 12,025 men, 354 men were diagnosed as having prostate cancer. The intervention had no noticeable effect on the incidence of prostate cancer, with similar number of cases observed in the intervention and control arms. Of the 354 prostate cancer cases, 75 had 3–8 blood samples taken as far back as ten years prior to diagnosis. The individuals deemed “controls” were selected among individuals not yet diagnosed as having either prostate or lung cancer by the time of analysis. The levels of free and total PSA were retrospectively assayed in the sera of 71 prostate cancer cases and 70 age-matched controls with similar duration in the study as the cases. These 71 prostate cancer cases were diagnosed between September 1988 and September 1995 inclusive. Since the cases and the controls were selected at the time of analysis, after the completion of the follow-up period of the trial, and the blood samples retrospectively assayed, this perfectly fits the setup of a case-control study that is embedded within a large cohort study with longitudinal exposure history available on cases and controls.
As the exposure variable, we use the natural logarithm of the total PSA (Ptotal) (secondary analyses with the negative logarithm of the ratio of free to total PSA (Pratio) reveal similar findings). Etzioni et al (1999) analyzed this data set by modeling the receiver operating characteristic (ROC) curves associated with both the biomarkers (Ptotal and Pratio) as a function of the time with respect to diagnosis. They observed that although the two markers performed similarly eight years prior to diagnosis, Ptotal was superior to Pratio in terms of its predictive performance at times closer to diagnosis. Thus, throughout the paper the term PSA is used to denote Ptotal as the exposure of interest.
Remark 2: Note that though the sampling scheme appears to be closely related to a nested case-control design (Lubin and Gail, 1984), there is a fundamental technical difference. In a nested case-control study, incidence density sampling is used, where at a failure time, say, t, at which the case occurs, a control is selected from the disease-free risk set i.e a set of individuals who are disease-free at time t. Thus a control at time t can become a case at a future time point. The usual analysis for a nested case-control design will thus use the partial/conditional likelihood framework, where the controls are selected from the disease-free risk sets at time t at which the case occurs (Prentice and Breslow, 1978). For time varying exposures (Samuelson, 1997; Essebag et al, 2005), one may need more than one control corresponding to each case under a nested case-control design for better finite sample performances. However, we are simply adopting an unmatched case-control design after the conclusion of the study and trying to create a measure of cumulative exposure when longitudinal exposure history is available for cases and controls. We are not using PSA measures directly as a time varying covariate in the disease risk model. If cases and controls are individually matched, say in terms of age and duration in the study, the unconditional logistic model can be extended to a stratified logistic regression model and similar Bayesian estimation can proceed with a prior distribution corresponding to the matched set specific nuisance parameters (Rice, 2008). We adjusted for age in our unconditional logistic regression model as the data set did not include enough information to identify the individually matched case-control pairs. Etzioni et al (1999) also adopted this unmatched analytic strategy by adjusting for matching covariates, instead of a conditional likelihood approach.
3 Model Specification
3.1 Notation
Let Yij be the jth exposure (PSA) observation recorded for the ith subject, aij the age of the ith subject when the jth PSA observation is collected, tij denotes the time (in years) of the jth PSA measurement relative to the time of diagnosis for the ith subject (i = 1, …, N; j = 1, …, ni). For cases, time of diagnosis is the time when cancer was detected and no PSA measurement at or after that time is used for our modeling purposes. For controls, time of diagnosis is synonymous to the last available observation time or the time of normal digital rectal examination (DRE). Denoting the age at diagnosis of the ith subject by , we have, . This relationship will be used below to simplify notation.
3.2 Model Framework
Our framework is composed of two models - (1) A Trajectory model for the longitudinal exposure profile and (2) a Disease Risk model for the effect of the exposure trajectory on the binary disease outcome. Inference on these two models will be done simultaneously, and is described in Section 4.
Our modeling framework resembles that of Zhang, Lin and Sowers (2007) who used a two-stage functional mixed model approach for modeling the effect of a longitudinal exposure profile on a continuous outcome. They proposed a linear functional mixed effects model for modeling the repeated measurements on the exposure values. The effect of the exposure profile on the continuous outcome was modeled via a partial functional linear model. They treated the unobserved, true subject-specific exposure trajectory as a functional covariate. For fitting purposes, they developed a two-stage nonparametric regression calibration method using smoothing splines. By using the relation between smoothing splines and mixed models, estimation at both stages was conveniently cast into a unified mixed model framework. The key difference between their framework and ours is that we use Bayesian inferential techniques to simultaneously estimate the parameters of the exposure and disease risk models. The adaptive knot selection allows for the smoothness to vary over the domain on which the function is defined. In addition, instead of a linear modeling framework, we use a combination of linear and logistic models since our exposure is continuous and the response is binary.
3.2.1 Exposure Trajectory Model
For the exposure trajectory model, we assume
| (1) |
where is the true (error-free) unobserved subject-specific exposure profile modeled as is the population mean function of the overall PSA trend as a function of age for all the subjects, gi(․) is the subject-specific deviation function reflecting the deviation of the ith subject specific profile from the mean population profile, and .
The reason for modeling exposure as a function of age is that, for a randomly chosen subject with unknown disease status, the PSA value at a certain time point should depend on the subject’s age at that time point, not their time with respect to diagnosis. In other words, the same exposure observation recorded at the same time relative to diagnosis for two subjects with different age values should not be treated as same.
We represent both f(aij) and gi(aij) using regression splines as follows:
| (2) |
where and are truncated polynomial basis functions of degrees p and q with knots (τ1, …, τK) and (κ1, …, κM) respectively. Typically, M ≤ K.
3.2.2 Disease Risk Model
The prospective disease risk model is assumed to be of the form
| (3) |
where L(․) is the logistic link function (L(u) = {1+exp(−u)}−1) and γ(t) is an unknown smooth function of time (with respect to diagnosis). We have treated age-at-diagnosis as a separate covariate in the disease model to account for the confounding effect of age on the association between PSA profile and the probability of disease. Lastly, c1 and c2 demarcate the length of the exposure history for the ith subject; e.g. c1 = 8 and c2 = 2 would imply that, for the ith subject, exposure observations recorded between 8 years to 2 years prior to diagnosis are being considered for analysis.
Remark 3: The function of interest in disease model (3) is γ(t): the influence function. This function provides the ability to capture a temporally varying relationship of a longitudinal trajectory on the current disease status of a subject. This is particularly important for studies dealing with the association of a longitudinal covariate/exposure and a continuous or discrete outcome. In our application, γ(t) captures the underlying association pattern between the PSA exposure trajectory and the probability of prostate cancer as a function of the time with respect to diagnosis. Another point to note is that by varying c1 and c2, we can select different lengths of PSA trajectories (across subjects) and can examine their effect on the current disease status. Similarly, as discussed in Section 6.3, using the disease risk model in (3), we can create odds-ratios comparing the effects of certain typical exposure trajectories, like a flat versus an exponential trajectory.
In the most general case, γ(t) can also be represented by a regression spline i.e.,
| (4) |
where and (ξ1, …, ξK*) are the knots.
Replacing (2) and (4) in the R.H.S of (3), we have
| (5) |
where and .
For pre-chosen degrees of the basis functions and a given set of knot locations and numbers, both Mi and Qi are matrices and are available in closed form. As will be explained in Section 4.3, adaptive knot selection techniques will be used to identify the optimal number and location of knots for Xi(․) and γ(․) respectively.
Remark 4: Since we had a relatively small data set, we have used the following simplified version of the trajectory model to analyze the prostate cancer dataset.
| (6) |
where . Consequently, the disease model simplifies to
| (7) |
The posterior calculations will be based on the above parametrization.
4 Posterior Inference
4.1 Likelihood Function
Let Yi = (Yi1, …, Yini)′ and Di denote the exposure vector and disease status while ai = (ai1, …, aini)′ and ti = (ti1, …, tini)′ be the observed values of age and time with respect to diagnosis for the ith subject respectively. So, the response vector for the ith subject is the pair (Yi, Di). Let be the set of unknown parameters corresponding to the exposure and disease models in (6) and (7). Since the optimal number and location of knots will be chosen in a data-driven manner, they will also be regarded as unknown parameters and will be simultaneously estimated through a fully Bayesian mechanism. Let k1 and k2 be the number of knots for the exposure and disease risk models respectively where 0 ≤ k1 ≤ K1 and 0 ≤ k2 ≤ K2, K1 and K2 being fixed. Let (τ1, …, τk1) and (ξ1, …, ξk2) denote the corresponding knot locations such that
The likelihood function is given by
| (8) |
where p(Yij|․) denotes the normal probability distribution corresponding to the trajectory model, is the normal distribution for the random subject specific slope coefficients while p(Di|․) is the Bernoulli distribution with success probability given by the logistic link function for the disease risk model in (7).
4.2 Priors
To complete the specification of our model, we assign prior distributions on the unknown parameters. We assume normal and inverse gamma priors for the parameters i.e and , where IG stands for inverse gamma density and (ai, bi)(i = 0, 1, 2, 3) are fixed hyperparameters. We use , a0 = 0.1, b0 = 0.1, a1 = 0.1, b1 = 0.1, a2 = 3, b2 = 3, a3 = 3 and b3 = 3. We also considered other values for (a2, b2) and (a3, b3) such as (0.1, 0.1), (1, 1), (2, 2), and (4, 4). However, inferences were not very sensitive to the choice of hyperparameters.
For the knot numbers k1 and k2, we put Poisson priors with means μ1 and μ2 such that μ1 = μ2 = 1. Since there is no reason a priori to favor knots at any particular locations on the domain of Xi(․) and γ(․), we put flat priors on both τ and ξ i.e
Since the knot locations and numbers are assumed to be independent, the joint prior distribution is given by π(k1, k2, τ, ξ) = π(k1)π(τ|k1)π(k2)π(ξ|k2).
4.3 Posterior Inference
Since the trajectory model in (1) has a linear form while the disease risk model (3) has a logistic structure, the resulting likelihood and posterior do not have a tractable closed form. To facilitate computations, we approximate the logistic distribution as a mixture of normals, using a well known data augmentation algorithm proposed by Albert and Chib (1993) for posterior sampling. For details, see the supplementary web appendix.
The joint posterior distribution of the parameters and the knots location/numbers is given by
where L(Ω, k1, k2, τ, ξ|y, D) is given in (8) and the other terms are the prior distributions on the parameters. Our main parameter of interest is ϕ, the effect of integrated exposure history on disease risk, as shown in (4). Since, the marginal posterior distribution of ϕ is analytically intractable, we have used a Reversible Jump MCMC (RJMCMC) algorithm (Green, 1995) to simultaneously sample the parameters, knot locations and positions in an integrated manner from their respective full conditionals (the details are given in the supplementary materials).
5 Model Comparison and Assessment
To compare models and determine their discriminative ability, we calculated the risk scores from the fitted “regression part” for the cases and controls ignoring the intercept. The reason for ignoring the intercept is that it is not meaningful given that we are using a prospective likelihood for a retrospective study. At iteration m of the MCMC sampler, the risk score for the ith individual is given by
where δ(m) is the sampled observation of δ at iteration m while and γ(m)(․) are the same for the exposure trajectory and the influence function. So, at the mth iteration, we have a vector of posterior estimates of risk scores for all the subjects, . We calculate the Spearman rank correlation coefficient between R(m) and the vector of original disease status vectors D = (D1, D2, …, DN) given by
| (9) |
where are the ranks and R̄(m)* is the mean of the ranks for the risk scores, and D̄* are defined similarly for the disease indicators, Di. Posterior summaries of ρ(m) can be taken as a measure of the model’s discriminative ability since these do not involve the intercept in the disease model unlike related approaches (e.g., posterior predictive loss and area under the curve (AUC)). Clearly, we want ρ to be close to one (and far from zero). As a tool for comparison, we compute posterior summaries of ρ for simpler and complex models and also for varying trajectory lengths as will be shown in Section 6.
For the mth iteration, we also compute the quantities
| (10) |
which are the averages of the posterior estimates of risk scores for the cases and controls (N0 and N1 being the number of controls and cases respectively). We can examine the posterior distribution of and and their difference. These quantities would give us a measure of the degree of separation between the cases and controls provided by our model and thus would inform on how well we can distinguish between the two groups.
6 Analysis of Prostate Cancer and PSA History
We use the semiparametric framework explained in Section 3 to analyze the prostate cancer dataset described in Section 2. Multiple observations on free and total PSA were obtained for 71 prostate cancer cases and 70 controls. For some subjects, observations were collected as far back as 10 years prior to diagnosis. We use the natural logarithm of total PSA (Ptotal) as our exposure of interest. Our principal aim is to examine whether past exposure observations can contribute significantly towards predicting the current disease status of a subject given his/her current exposure information. In doing so, we will also test how differential lengths of the PSA trajectories affect the current probability of disease for a particular individual.
As mentioned in Remark 4 in Section 3, we have used a simplified version of the trajectory and disease risk models given in (6) and (7) to analyze our dataset. In doing so, we examined the effect of varying lengths of exposure trajectories on the current disease state by choosing different values of c1 and c2 in the disease model.
We did a small sensitivity analysis by changing the hyper parameters of the inverse-Gamma priors on and . The results were not very sensitive to the choice of these parameters (results not shown).
6.1 Overall Model Comparison
We calculated the posterior means and 95% confidence intervals of the risk measures mentioned in (9) and (10) for the different exposure intervals. These are denoted by (a) ρ: Spearman’s rank correlation coefficient between the risk scores and disease status for all the subjects; (b) R1: Mean of the risk scores for cases; (c) R0: Mean of the risk scores for controls and (d) Rd = R0 − R1: difference between the mean risk scores for the controls and cases. The results are shown in Table 1. Based on these measures, we conclude that the disease risk model fitted to the exposure interval I = [−10, 0] had the best performance. In particular, the model with this interval had the highest negative values of the difference Rd(−2.33) (the greatest separation of the risk scores between the cases and controls) and the largest value for Spearman’s correlation, ρ(0.68); in an absolute sense, a correlation of 0.68 is quite large. In the next section, we fit some simpler models to illustrate the increased information that can be gained from our approach.
Table 1.
Values of the risk score measures corresponding to different intervals. The 95% credible intervals are also given for the optimal model based on I = (−10, 0) and the simpler alternative models Mj : j = 0, 1, 2.
| Risk Score Measures | ||
|---|---|---|
| Intervals | Rd | ρ |
| (−3, 0) | −2.06 | 0.66 |
| (−5, 0) | −2.12 | 0.67 |
| (−8, 0) | −2.27 | 0.67 |
| (−10, 0) | −2.33 (−3.26, −1.55) | 0.68 (0.64, 0.71) |
| (−10, −5) | −1.98 | 0.65 |
| (−12, 0) | −2.23 | 0.67 |
| M0 | −0.28 (−0.74, 0.18) | 0.08 (−0.11, 0.11) |
| M1 | −2.04 (−2.76, −1.42) | 0.66 (0.65, 0.67) |
| M2 | −1.95 (−2.73, −1.30) | 0.65 (0.62, 0.69) |
6.1.1 Comparison with Simpler Models
The disease risk model as given in (7) is quite general in that it takes into account age (at diagnosis) and the PSA trajectory of a subject into account and also incorporates the influence pattern of the trajectory on the disease probability. Clearly, simpler versions of this framework are possible. As such, we fit the following three models:
M0 : .
M1 : .
M2 : ,
where is the last observed PSA value for subject i. The models correspond to, respectively, ignoring any PSA information and only using age at diagnosis, using the last observed PSA value and age at diagnosis, and using the area under the PSA curve as a covariate with age at diagnosis. For each of these three models, Table 1 shows the posterior estimates of the risk measures. Model M0 that just included age at diagnosis was unable to separate the cases and controls at all. Models M1 and M2 did well but provided less separation of the risk scores and a lower correlation. In addition, Model M1 provided a similar correlation and separation to the general model with the interval (−3, 0) which is not surprising as this interval typically contained the last observed PSA value. Overall, these results support the notion that the semiparametric modeling implemented here for incorporating the exposure (or PSA) trajectory/history was worthwhile for this data, though the strength of evidence for the complex model was limited to some extent by the small sample size and the ‘noisy’ observed PSA trajectories.
6.2 Shapes of the trajectory and influence functions
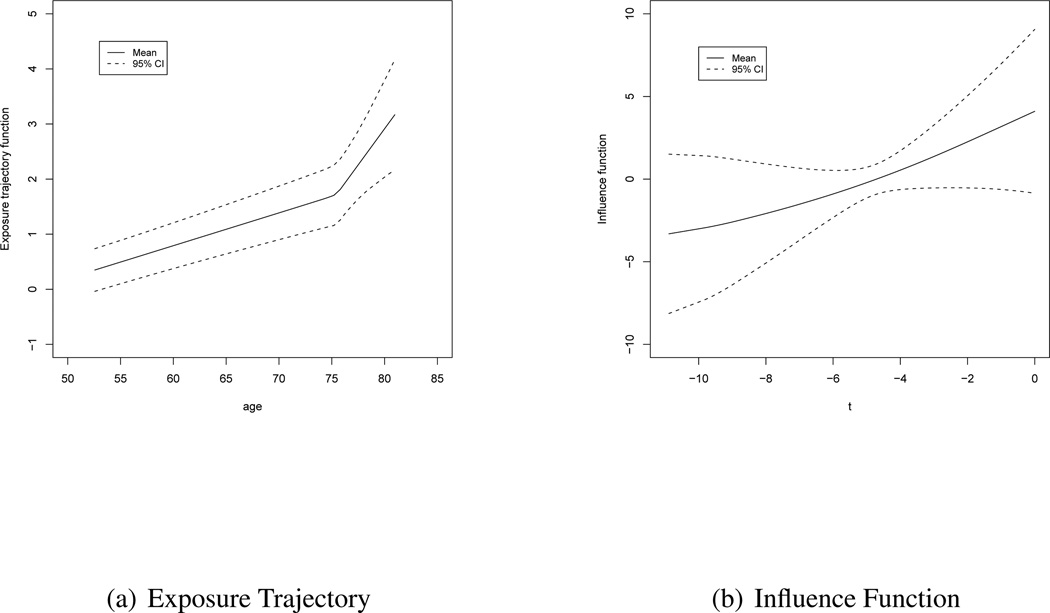
Figures 1(a) and (b) show the plots of the population mean exposure trajectory and the influence function and the corresponding 95% confidence bands as obtained from the posterior samples of the parameters and knots. The former is plotted against age while the latter is plotted against the time with respect to diagnosis. The posterior distribution of the number of knots for both functions placed most of their mass at one knot (0.93 for the exposure model and 0.70 for the disease model) with the non-linearity evident a little after age 75 for the exposure trajectory and a slight nonlinearity in the influence function (though it is close to linear). The posterior mean of the exposure trajectory confirms the fact that the PSA observations tend to increase steadily with age. The pattern is more or less linear for the entire age-range. However, there is a sharp upward turn near about age 77 (as mentioned above) when the PSA values increases further. On the other hand, the influence of the PSA profile on the current disease status has an increasing pattern as we move closer to the point of diagnosis. This is intuitive since the effects of exposure observations collected closer to the point of diagnosis would be expected to have a higher influence (weight) on the current disease status than those collected further back in time. In addition, the sign of γ(t) (see Figure 1(b) with positive values for the first five years before diagnosis, and negative values for second five years) indicates that the function, γ(t) captures the differential direction of the effect of PSA values closer to diagnosis versus those farther back in time.
Figure 1.
Plot of the exposure trajectory against age and the influence profile against the time with respect to diagnosis for the PSA data
6.3 Inference on odds ratios
To better understand the relationship between PSA trajectory and the probability of prostate cancer, we compute several odds ratios. In particular, we compute the posterior distribution of the log-odds of prostate cancer corresponding to some reasonable shapes of exposure trajectories (in what follows, comparing a trajectory Xi to a trajectory Zi) based on our data.
In the following, we denote the different comparisons by C1, C2, C3 and C4. For each of these comparisons, we denote by l and u, the lower and upper limits of the trajectories. For C1–C3, the level of the baseline (flat) trajectory Xi is the average of the lower and upper limits of the increasing trajectory, Zi i.e (l + u)/2. Based on our data, we choose l = 0.1 and u = 0.9 (these are the lowest and highest values of PSA for one of the subjects in the dataset) and l = .039 and u = 1.37 (these are the 25th and 75th percentiles of the observed PSA values, respectively).
C1 : .
Here we compare the log-odds of disease corresponding to a flat trajectory to an exponentially increasing one. The values of ν and ζ that yield l and u are given by
The log-odds ratio for this comparison is given by
C2 : .
Here we compare the log-odds of disease corresponding to a flat trajectory to a linearly increasing one. The values of ν and ζ that yield l and u are given by
The log-odds ratio for this comparison is given by
C3 : .
Here we compare the log-odds of disease corresponding to a flat trajectory to one which is linear in the logarithmic scale. The values of ν and ζ that yield l and u are given by
The log-odds ratio for this comparison is given by
C4 : .
Here we compare the log-odds of disease corresponding to a exponentially increasing trajectory to a linearly increasing one. The values of ν and ζ that yield l and u are given by
The log-odds ratio for this comparison is given by
Table 2 reports the posterior means and 95% credible intervals of the log-odds ratios for the above four comparisons and the two choices of upper and lower limits. The log-odds ratios for the first three comparisons (horizontal-exponential, horizontal-linear and horizontal-logarithmic) are marginally significant (with credible intervals barely covering zero) and fairly similar. The similarity between these three is not surprising since the form of the influence function γ(t) captures a contrast between early and late PSA values and the comparison of each is with respect to a stable (flat) PSA trajectory at the mid point of the increasing ones (in fact, if the level of the flat trajectory is set at the lower limit of the increasing ones, i.e at l, all the log-odds are more extreme and significant). The log odds ratios for both choices of the lower and upper limits, (l, u) are quite large and indicate a much higher odds of prostate cancer for an increasing PSA trajectory versus one that is stable. These odds ratio measures are not comparable with a simple logistic regression model that is linear in the last available PSA observation (estimated log OR of 1.2) since here we are using the entire longitudinal trajectory and an influence function which greatly affects the magnitude and interpretation of the point estimates obtained. The odds ratio for the fourth comparison, a linear trajectory versus an exponentially increasing one (that both start and end at the same values), is also marginally significant for both cases and shows the power of this modeling approach with the ability to utilize the actual shape of the trajectories to better estimate the odds of prostate cancer.
Table 2.
Posterior means and corresponding 95% credible intervals of the log-odds ratios for comparing different shapes of the exposure trajectories. Here C1: horizontal-exponential, C2: horizontal-linear, C3: horizontal-logarithmic and C4: linear-exponential exposure profiles under two different specifications of the odds ratios (a,b).
| Comparisons | ||||
|---|---|---|---|---|
| (a,b) | C1 | C2 | C3 | C4 |
| (.1,.9) | 4.51 (−0.25, 11.04) | 4.80 (−0.08, 11.64) | 4.79 (−0.06, 11.61) | 0.29 (−0.22, 0.74) |
| (.039,1.37) | 6.83 (−0.55, 16.84) | 8.00 (−0.13, 19.42) | 8.00 (−0.11, 19.36) | 1.2 (−0.12, 2.8) |
Overall, our results indicate that for future retrospective assays of stored serum samples for individuals at risk for prostate cancer, it would be informative to go back up to 10 years prior to diagnosis.
7 Discussion
Using longitudinal exposure trajectories in a case-control design is a relatively unexplored area. Recent developments in the area of semiparametric and nonparametric regression analysis have provided techniques to capture exposure trajectories that have complicated and unknown functional forms. We have used free knot regression splines in modeling the exposure trajectories for the cases and the controls. However, the trajectory model in our application lacks a random (subject specific) intercept due to the small sample size and lack of heterogeneity. Our framework can be used even when exposure observations are collected at different time points across subjects i.e when the study design is unbalanced in nature. The exposure trajectory is used as the predictor in a prospective logistic model for the binary disease outcome. We have additionally modeled the slope parameter of the disease risk model as a regression spline to account for any time varying influence pattern of the exposure trajectory on the current disease status. We have integrated an adaptive knot selection mechanism by which the optimal position and locations of the knots for both the exposure trajectory and influence functions are simultaneously selected in a data-driven manner. Overall, the proposed method appropriately accounts for the generated uncertainty of this multi-level approach.
In order to simplify the analysis, we used the logit-mixture of normal approximation (Albert and Chib, 1993). We also established that the Bayesian equivalence results of Seaman and Richardson (2004) holds for our framework, thus allowing us to use a prospective logistic model having fewer nuisance parameters although the data set was collected retrospectively.
We analyzed our data using different lengths of exposure trajectories. In doing so, we have concluded that past exposure observations do provide significant information towards predicting the current disease status of a subject. We performed model comparison and assessment by calculating risk scores corresponding to the cases and controls and computing correlations which are not influenced by using the prospective likelihood (as opposed to the retrospective one). These criteria indicated that models with longer exposure trajectories tend to perform better than those with shorter trajectories and that the relationship between the PSA trajectory and disease is complex. In fact, we concluded that the model incorporating exposure observations recorded 10 years prior to diagnosis results in the best fit to the dataset. Based on the model comparison tools we used, it seemed that PSA observations collected prior to 10 years before diagnosis provide minimal additional information in explaining the current disease status above and beyond those collected up to 10 years prior to diagnosis (although the available exposure data beyond 10 years was quite sparse). We have also confirmed that conditional on age at diagnosis, the exposure trajectory contains significant amount of information on the current disease status of a subject and thus should be included in the disease risk model. We showed that by doing so, the model performance improves significantly compared to last observation carried forward analysis.
Some interesting extensions remain under consideration for future research. For richer datasets, it will be interesting to implement the completely flexible formulation with the subject-specific deviation functions also represented as regression splines. Extending the analytic approaches to the set-up of a serial case-control study as in Park and Kim (2004), which has the additional complexity of correlated time varying response variable, is also an open problem.
Supplementary Material
Acknowledgements
This research was supported by National Institutes of Health grant CA-85295, P30-AG028740, NIH R03 CA156608, NSA grant MSPF-07G-097, and NSF grant DMS 1007494. The work of Dr. Sungduk Kim was supported by the intramural research program of National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health and Human Development. The authors thank Kenneth M. Rice, the editor, the associate editor, and the reviewers for many insightful comments leading to substantial improvements in the article.
Footnotes
Supplementary Materials
Web Appendices, Tables, and Figures referenced in Sections 1, 4.3, and 6.1–6.3 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.
REFERENCES
- Albert JH, Chib S. Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association. 1993;88:669–679. [Google Scholar]
- Botts CH, Daniels MJ. A flexible approach to Bayesian curve fitting. Computational Statistics and Data Analysis. 2008;52:5100–5120. doi: 10.1016/j.csda.2008.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow NE. Statistics in Epidemiology : The case control study. Journal of American Statistical Association. 1996;91:14–30. doi: 10.1080/01621459.1996.10476660. [DOI] [PubMed] [Google Scholar]
- Breslow NE, Day NE, Halvorsen KT, Prentice RL, Sabai C. Estimation of multiple relative risk functions in matched case-control studies. American Journal of Epidemiology. 1978;108:299–307. doi: 10.1093/oxfordjournals.aje.a112623. [DOI] [PubMed] [Google Scholar]
- Cornfield J. A method of estimating comparative rates from clinical data: applications to cancer of the lung, breast, and cervix. Journal of the National Cancer Institute. 1951;11:1269–1275. [PubMed] [Google Scholar]
- DiMatteo I, Genovese CR, Kass RE. Bayesian curve fitting with free knot splines. Biometrika. 2001;88:1055–1071. [Google Scholar]
- Ernster VL. Nested case control studies. Preventive Medicine. 1994;23:587–590. doi: 10.1006/pmed.1994.1093. [DOI] [PubMed] [Google Scholar]
- Essebag V, Platt RW, Abrahamowicz M, Pilote L. Comparison of nested case-control and survival analysis methodologies for analysis of time-dependent exposure. BMC Med Res Methodol. 2005 doi: 10.1186/1471-2288-5-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etzioni R, Pepe M, Longton G, Hu C, Goodman G. Incorporating the time dimension in receiver operating characteristic curves : A case study of prostate cancer. Medical Decision Making. 1999;19:242–251. doi: 10.1177/0272989X9901900303. [DOI] [PubMed] [Google Scholar]
- Freedman LS, Oberman B, Sadetzki S. Using time dependent covariate analysis to elucidate the relation of smoking history to Warthin’s tumor risk. American Journal of Epidemiology. 2009;170(9):1178–1185. doi: 10.1093/aje/kwp244. [DOI] [PubMed] [Google Scholar]
- Green PJ. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82:711–732. [Google Scholar]
- Lewis MA, Heinemann LAJ, MacRae KD, Bruppacher R, Spitzer WO. The increased risk of venous thromboembolism and the use of third generation progestagens : Role of bias in observational research. Contraception. 1996;54:5–13. doi: 10.1016/0010-7824(96)00112-6. [DOI] [PubMed] [Google Scholar]
- Lindstrom MJ. Penalized estimation of free knot splines. Journal of Computational and Graphical Statistics. 1999;8:333–352. [Google Scholar]
- Liu JS. The collapsed Gibbs sampler in Bayesian computations with applications to a gene regulation problem. Journal of the American Statistical Association. 1994;89:958–966. [Google Scholar]
- Lubin JH, Gail MH. Biased selection of controls for case-control analyses of cohort studies. Biometrics. 1984;40(1):63–75. [PubMed] [Google Scholar]
- Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute. 1959;22:719–748. [PubMed] [Google Scholar]
- Moulton LH, Monique GL. Latency and time-dependent exposure in a case-control study. Journal of Clinical Epidemiology. 1991;44(9):915–923. doi: 10.1016/0895-4356(91)90054-d. [DOI] [PubMed] [Google Scholar]
- Mukherjee B, Sinha S, Ghosh M. Handbook of Statistics. Vol 25. Bayesian Thinking: Modeling and Computation; 2005. Bayesian analysis for Case Control studies - A review article; pp. 793–819. [Google Scholar]
- Park E, Kim Y. Analysis of longitudinal data in case control studies. Biometrika. 2004;91:321–330. [Google Scholar]
- Prentice RL, Breslow NE. Retrospective studies and failure time models. Biometrika. 1978;65:153–158. [Google Scholar]
- Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66:403–411. [Google Scholar]
- Rice K. Equivalence between conditional and random-effects likelihoods for pair-matched case-control studies. Journal of the American Statistical Association. 2008;103(481):385–396. [Google Scholar]
- Samuelson SO. Pseudolikelihood approach to analysis of nested case-control studies. Biometrika. 1997;84:379–394. [Google Scholar]
- Seaman SR, Richardson S. Bayesian analysis of case-control studies with categorical covariates. Biometrika. 2001;88:1073–1088. [Google Scholar]
- Seaman SR, Richardson S. Equivalence of prospective and retrospective models in the Bayesian analysis of case-control studies. Biometrika. 2004;91:15–25. [Google Scholar]
- Thomas DC. Statistical methods for analyzing effects of temporal patterns of exposure on cancer risks. Scandinavian Journal of Work, Environment and Health. 1983;9:353–366. doi: 10.5271/sjweh.2401. [DOI] [PubMed] [Google Scholar]
- Thomas DC. Models for exposure-time-response relationships with applications to cancer epidemiology. Annual Review of Public Health. 1988;9:451–482. doi: 10.1146/annurev.pu.09.050188.002315. [DOI] [PubMed] [Google Scholar]
- Zelen M, Parker RA. Case-control studies and Bayesian inference. Statistics in Medicine. 1986;5:261–269. doi: 10.1002/sim.4780050307. [DOI] [PubMed] [Google Scholar]
- Zhang D, Lin X, Sowers MF. Two stage functional mixed models for evaluating the effect of longitudinal covariate profiles on a scalar outcome. Biometrics. 2007;63:351–362. doi: 10.1111/j.1541-0420.2006.00713.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.