Analytical optimal controls for the state constrained addition and removal of cryoprotective agents

Abstract

Cryobiology is a field with enormous scientific, financial and even cultural impact. Successful cryopreservation of cells and tissues depends on the equilibration of these materials with high concentrations of permeating chemicals (CPAs) such as glycerol or 1,2 propylene glycol. Because cells and tissues are exposed to highly anisosmotic conditions, the resulting gradients cause large volume fluctuations that have been shown to damage cells and tissues. On the other hand, there is evidence that toxicity to these high levels of chemicals is time dependent, and therefore it is ideal to minimize exposure time as well. Because solute and solvent flux is governed by a system of ordinary differential equations, CPA addition and removal from cells is an ideal context for the application of optimal control theory. Recently, we presented a mathematical synthesis of the optimal controls for the ODE system commonly used in cryobiology in the absence of state constraints and showed that controls defined by this synthesis were optimal. Here we define the appropriate model, analytically extend the previous theory to one encompassing state constraints, and as an example apply this to the critical and clinically important cell type of human oocytes, where current methodologies are either difficult to implement or have very limited success rates. We show that an enormous increase in equilibration efficiency can be achieved under the new protocols when compared to classic protocols, potentially allowing a greatly increased survival rate for human oocytes, and pointing to a direction for the cryopreservation of many other cell types.

Introduction

The economic, scientific and even cultural impact of cryobiology is immense¹: billions of dollars are invested in frozen cells and tissues for use in cell culture transport [19], facilitation of agricultural and human reproduction [31], improvements in human and animal medicine [25], and bioengineering [18]. Arguably more important than cooling and warming rates, the addition and removal of cryoprotective agents (CPAs) to and from cells [26] is a critical and limiting factor in cryopreservation success—current cryopreservation protocols are limited by the inability to equilibrate cells with sufficiently high concentrations of CPAs to cause an intracellular glass to form while cooling. The transport of CPAs across cell membranes is well described by a system of coupled nonlinear ordinary differential equations, and is often limited by the existence of cell-specific volume or concentration constraints [26]. To date only heuristic optimizations of CPA addition and removal protocols have been published [13,24,23]. Here we show that optimal control theory can be successfully applied to the introduction and subsequent removal of cryoprotective agents. Moreover, while applying the general optimization theory outlined recently [6], we are able to add the natural cell volume and concentration constraints that are encountered in the process of cryoprotective agent addition and removal [19]. Here we show that for a large set of parameters, at least a five-fold time reduction can be made over classical techniques. We then provide a specific application to human oocytes, where the time to safely equilibrate oocytes with vitrification level ethylene glycol (e.g. more than 40 molal) is reduced by a factor of five to twenty.

There are two conflicting factors in the development of a CPA addition or removal protocol—the exposure time to multimolal concentrations of CPAs and damaging cell and water volume excursions (Fig. 1)—which point to the existence of an optimal protocol and necessitate an algorithm that provides the optimized CPA addition and removal procedure when the membrane permeability characteristics and the osmotic or volumetric tolerance limits of a specific cell type are known. Often CPAs are added and removed in gradual steps, whose durations and concentrations are empirically based [15]. Heuristic methods for the optimization of CPA addition and removal, deriving protocols where the CPA concentration is varied continuously [23,24]. These protocols have produced improved but not optimal protocols limited in the general applicability of the technique.

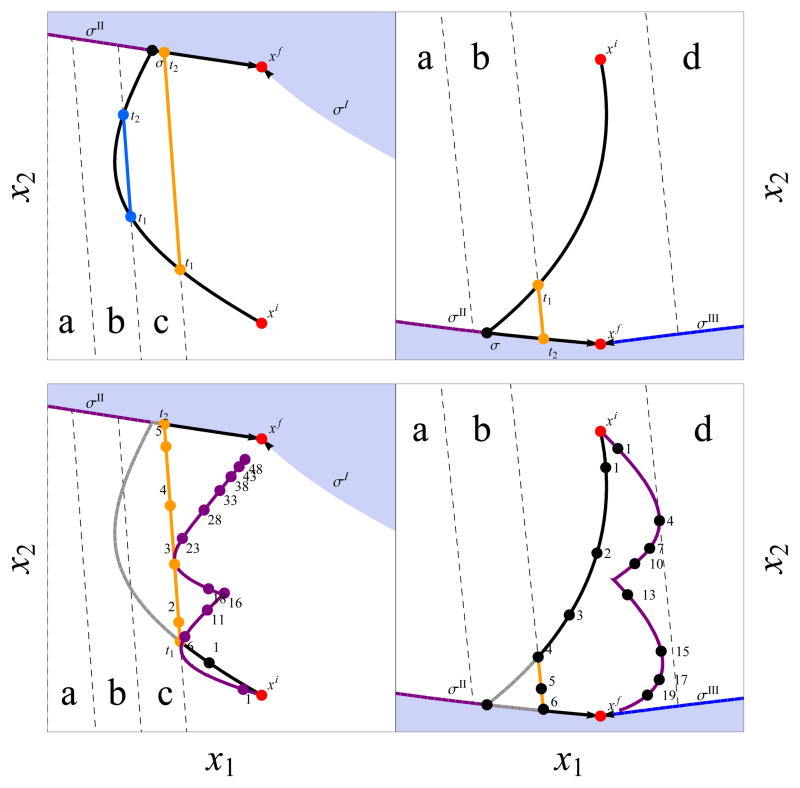
Fig. 1.

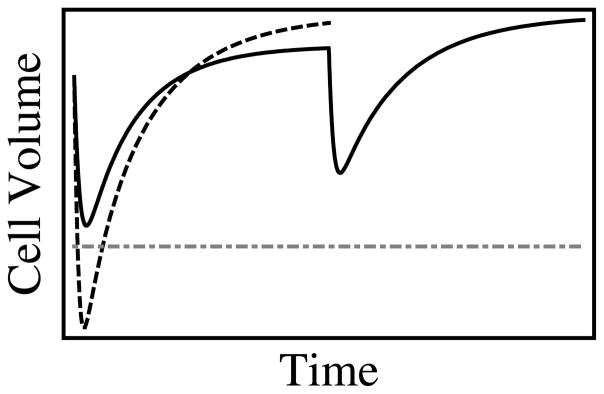
Plot of the effects of two different CPA addition protocols. A hypothetical cell is equilibrated with a goal concentration C of a permeating CPA. This cell has a lower limit to which it can contract without damage. If the cell is exposed abruptly to C, the efflux of water causes it to shrink below this limit, causing cell death. Alternatively, if the cell is exposed to C/2 and then C, the cell does not exceed the limit, but is exposed to the chemicals for a longer period of time. We wish to find an optimal balance between these two competing effects.

We wish to control the extracellular concentrations of permeating and non-permeating solutes (M₂ and M₁, respectively) such that cells are equilibrated at a goal state in the shortest time while remaining within predefined state-constraints. For analytical simplicity we will use the solute-solvent transmembrane flux model described by Jacobs [17] and commmonly used in cryobiology [21]. This model recently was noted to encompass a very large array of membrane transport phenomena [16]. After simplifying the osmotic pressure to a single term in a virial expansion and non-dimensionalizing (cf. [20]) we have the system

$$\begin{array}{l}\frac{{dx}_1}{ds}=-M_1-M_2+\frac{x_{\text{np}}+x_2}{x_1},\\ \frac{{dx}_2}{ds}=b\left(M_2-\frac{x_2}{x_1}\right),\end{array}$$ (1)

where x₁ and x₂ are the intracellular water volume and moles of solute, respectively, x_np is the (assumed fixed) moles of nonpermeating solute, b is a unitless relative permeability constant, and s is a dimensionless temporal variable. Following an approach we have previously described [5], we factor out $x_1^{-1}$ to facilitate a time-transform with

$$s=q(t):={\int }_0^t{x}_1(\xi )d\xi ,$$ (2)

resulting in a system that is linear in the concentration and state variables (see Table 1 for parameter definitions):

$$\begin{array}{l}{\stackrel{.}{x}}_1=-(M_1+M_2)x_1+x_2+x_{\text{np}},\\ {\stackrel{.}{x}}_2={bM}_2{x}_1-{bx}_2,\end{array}$$ (3)

or ẋ = A(M)x+x_npe₁, for x:= (x₁,x₂), where $\stackrel{.}{x}=\frac{dx}{dt}$, e₁ = (1,0)^T, and

Table 1.

Definition of parameters

Variable	Non-dimensional parameter description
x1	Cell water volume
x2	Cell permeating solute mass
xnp	Cell non-permeating solute mass
xi or xf	Initial or final state values, respectively
M1	Extracellular non-permeating solute concentration
M2	Extracellular permeating solute concentration
M̄i	Maximal solute concentration
b	Unitless relative cell permeability parameter
γ	Partial molar volume of the permeating solute
k	Upper or lower cell volume limit
τ,t1,t2	Switching times

$$A(M)=\left(\begin{array}{cc}-M_1-M_2& 1\\ {bM}_2& -b\end{array}\right).$$

Optimal control

We set M̄_i > 0 for i = 1, 2, the admissible control parameter set

$$\text{CP}=\{M=(M_1,M_2)\in {ℝ}^2:0\le M_i\le {\overline{M}}_i\text{for}i=1,2\},$$ (4)

and the state space S ⊂ (0,∞)×[0,∞) (note x₁ > 0). In addition, we define x(t) = x(t; x₀,M) to be the solution of the initial value problem (3) and

$${\mathcal{C}}_y(t)=\{x_0\in S:x(t):=x(t;x_0,u)=y\},$$

to be the set of initial conditions that can be steered to y ∈ S at time t via a measurable, admissible control function M: ℝ⁺ → CP.

Define Γ = (γ₁,γ₂)^T ∈ ℝ², which allows the representation of water volume, total cell volume, or concentration of permeating solute constraints in terms of x₁ and x₂. To wit, with γ₁ = 1 and γ₂ equal to the partial molar volume of the permeating solute, Γ · x represents the total “osmotically active” volume of a cell; the pair γ₁ = 1, γ₂ = 0, represents the total water volume of the cell, and by choosing sgnγ₁ ≠ sgnγ₂, we may represent bounds on concentration such as x₂/x₁ ≤ 1.0. For the remainder of this manuscript we set γ₁ = 1. We have a time-optimal control problem of steering an initial state xⁱ to a final state x^f in minimal “real” time using controls in the admissible set , the set of measurable functions M: ℝ → CP, and formally we may now define the optimal control problems:

Problem 1

Given an initial state xⁱ in the state space S and final state x^f ∈ S, the set of admissible controls and defining s^* ∈ ℝ to be the first time that x(s^*) = x^f for the solution of the previously defined initial value problem defined in system (1), determine a control that minimizes s^* over M ∈ 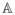, subject to constraints Γ · x +k ≤ 0 for constant k ∈ ℝ.

Using the time-transform function q in (2), we have the equivalent problem

Problem 2

Given an initial state xⁱ in the state space S and final state x^f ∈ S, the set of admissible controls 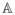and defining t^* ∈ ℝ to be the first time that x(t^*) = x^f for the solution of the previously defined initial value problem

$$\stackrel{.}{x}=f(x,M)=A(M)x+x_{np}{e}_1,x(0)=x^i,$$ (5)

determine a control that minimizes the cost functional

$$J(M):=s^{\ast }=q(t^{\ast })={\int }_0^{t^{\ast }}{x}_1(t)dt$$ (6)

over 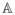, subject to constraints

$$\mathit{\Gamma }\cdot w+k\le 0,$$ (7)

for constant k ∈ ℝ.

The existence of an optimal control along with the equivalence of these problems is proved in [6].

Though numerical approaches exist for solving Problem 2 with nonlinear and multiple state constraints using classical numerical optimal control techniques, here we will construct analytically the optimal control in the most commonly encountered case where there are total cell volume constraints of the form k_* ≤ x₁ + γ₂x₂ ≤ k^* corresponding to upper and lower osmotic tolerance limits, where the initial and final water volumes are equal, i.e. $x_1^f=x_1^i=x_1^{\ast }$, and either $x_2^i=0$ and $x_2^f=x_2^{\ast }$, or $x_2^i=x_2^{\ast }$ and $x_2^f=\epsilon$ for ε small. These two cases correspond to the addition or the removal of CPA, respectively. In the latter case, one must set $x^f=(x_1^{\ast },\epsilon )$ because the dynamics of the system only allow an asymptotic approach to the x₁-axis. Furthermore, we assume the bounds 0 ≤ M₁(t) ≤ M̄₁ and 0 ≤ M₂(t) ≤ M̄₂, where M̄_i are maximal physical or practical concentration limits (e.g. M̄₁ may be limited by the salt or sucrose saturation point and M̄₂ may be limited by a maximum practical viscosity), and because of natural equilibration constraints of the system (cf. [6]) we restrict xⁱ and x^f so that $x_2^{\delta }<x_1^{\delta }{\overline{M}}_2$ and $x_{np}>x_1^{\delta }{\overline{M}}_1$ (δ = i or f).

We define ${\varphi }_t^{\lambda }$ to be the solution of (3) with control M = λ at a time t and the initial condition ${\varphi }_0^{\lambda }(x)=x$. We define the curves

$${\sigma }^j:=\{x\in {({ℝ}^{+})}^2:x\in {\varphi }_t^{M^j}(x^f),t<0\},\text{for}j=I,II,\text{and}\mathit{III},$$ (8)

where M ^j for j = I,II, and III are defined in Table 2. We also define the time τ > 0 to be the first time that ϕ_τ ∈ σ^j, and the time t^* > 0 to be the total time required to reach x^f. In [6] we synthesized optimal controls based on the Pontryagin Maximum Principle (PMP) [30] and proved optimality based on a theorem of Boltayanski [7] but did not provide an explicit example or show how to incorporate constraints.

Table 2.

Definition of controls

Control	M1(t)	M2(t)
MI	0	M̄2
MII	0	0
MIII	M̄1	0

For the unconstrained case, the optimal CPA addition and removal controls, respectively, are given by

$$M_A(t)=\{\begin{array}{cc}{M}^I,& t\le \tau ,\\ M^{II},& \tau <t<t^{\ast },\end{array}\text{and}{M}_R(t)=\{\begin{array}{cc}{M}^{\mathit{III}},& t\le \tau ,\\ M^{II},& \tau <t<t^{\ast }.\end{array}$$

While these controls are optimal, they come at the cost of possibly excessive volume excursions (see Fig. 2). To remedy this possibility, we will optimize in the presence of constraints, which correspond to lines in the state space

Fig. 2.

Plot of system geometry and hypothetical volume constraints defined by lines a, b, c and d (each associated with a different k value (c.f. equation (7)). Regions within each sub-figure are defined by the lines σⁱ, i = I, II, III, IV from equation (8). The left and right sub-columns represent CPA addition and removal, respectively, and the top left and right figures represent the potential cases from equations (14) and (18), respectively. These cases come from changing constraint lines a through d. Constraint line a is inactive, there is only one switching time τ, and the path is represented by the black line. When constraint line b is active, the unconstrained curve intersects b at times t₁ and t₂; for t₁ ≤ t ≤ t₂, the optimal path is along the constraint boundary that is represented by the blue line. When constraint line c is active, the unconstrained curve intersects c at time t₁ and t₂, and for t₁ ≤ t ≤ t₂ the optimal path is along the constraint boundary, represented by the orange line. In both latter cases, for t > t₂, the optimal trajectory again is the unconstrained curve, represented by the black line. The bottom left and right figures show comparison of constrained optimal (black) and traditional controls (purple) under typical parameters, where numbers are unitless relative times and the solid gray line shows the unconstrained trajectory for reference.

$${\ell }_{\ast }:=\{(x_1,x_2)\in {({ℝ}^{+})}^2:{\gamma }_2{x}_2=-x_1+k_{\ast }\}$$ (9)

and

$${\ell }^{\ast }:=\{(x_1,x_2)\in {({ℝ}^{+})}^2:{\gamma }_2{x}_2=-x_1+k^{\ast }\}.$$ (10)

In practice, if M̄₁ and M̄₂ are large enough, it is enough to only use constraints of the form k_* ≤ x₁ + γ₂x₂ for both CPA addition and removal protocols. We state this in a lemma which follows directly from the derivation of equations (11) and (15) below.

Lemma 1

In the CPA addition case, where xⁱ = (x₁(0), 0), x^f = (x₁(0), η), η > 0, and Γ · xⁱ < k^*, if ${\overline{M}}_2>\frac{(1-{\gamma }_{2}b)\eta +x_{\text{np}}}{(1-b{\gamma }_2)x_1^i}$, then ${\varphi }_t^{M^I}(x^i)\cap {\ell }^{\ast }=\varnothing$. In the CPA removal case, where xⁱ = (x₁(0), η), x^f = (x₁(0), ε), ε small, and Γ · xⁱ < k^*, if ${\overline{M}}_1>\frac{(1-b{\gamma }_2)\eta +x_{\text{np}}}{k^{\ast }-{\gamma }_2\eta }$, then ${\varphi }_t^{M^{\mathit{III}}}(x^i)\cap {\ell }^{\ast }=\varnothing$.

In both addition and removal cases we will define at most three times t₁ < t₂ and τ corresponding to the switching times for control schemes. Note that these are times in the transformed space; we must use the s = q(t) function in display (2) to determine “real” switching times. There are three possibilities to the dynamics of the optimal control problem: 1) the state constraint is inactive and the bang-bang optimal control outlined above is optimal; 2) the state constraint is active but ${\varphi }_t^{\lambda }(x^f)\notin {\ell }_{\ast }$ for all t ≤ τ − t^*; 3) the state constraint is active and ${\varphi }_t^{\lambda }(x^f)\in {\ell }_{\ast }$ for some t ≤ τ − t^*. These cases are shown in figure (2). Because of the above argument, it follows that in cases (2) and (3) there are times t₁ and t₂ where the unconstrained optimal path intersects the constraint line. The constrained Pontryagin Maximum Principal states that if the optimal control M exists, there is a costate variable p such that for t ∈ (t₁, t₂), M ∈ 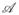maximizes the Hamiltonian H(x, p, M):= f(x, M) · p + x₁, and that the constraint remains active. Moreover, we must have the jump condition ${lim}_{t\to t_1^{+}}p(t)={lim}_{t\to t_1^{-}}p(t)$. Using this fact, we are able to deduce the optimal controls. For t ∉ (t₁, t₂) the controls are the same as for the unconstrained system. For t ∈ (t₁, t₂), we must maximize H(x, p, M) with γ₂x₂ = −x₁+k_*, which is equivalent to maximizing

$$\underset{M_1,M_2}{max}\{-M_1{p}_1(k_{\ast }-{\gamma }_2{x}_2)+M_2({bp}_2-p_1)(k_{\ast }-{\gamma }_2{x}_2)\}.$$

Derivation of CPA addition optimal controls with an active constraint

In the CPA addition case, from our previous analysis [6] p₁(t₁) > 0 and p₂(t₁) > p₁(t₁)/b, so p₁(t₁) and p₂(t₁) are both positive. Thus, since k_* − γ₂x₂ > 0, we must choose M₁ as small as possible and M₂ as large as possible with the active constraint. Thus, if M̄₂ is large in the sense of Lemma 1, we may set M₁ ≡ 0. Because of this, we can explicitly solve system (3) with Γ · x = k_* for M₂(t). To do so, note Γ · ẋ = 0, which means we have ẋ₁ = −γ₂ẋ₂, or

$$-M_2{x}_1+x_2+x_{\text{np}}=-{\gamma }_2(M_2{bx}_1-{bx}_2),$$

which we solve for

$$M_2=\frac{(1-{\gamma }_{2}b)x_2+x_{\text{np}}}{(1-b{\gamma }_2)x_1},$$ (11)

and substitute this back into the system (3) with M₁ = 0 to get

$$\begin{array}{l}{\stackrel{.}{x}}_1={\gamma }_2{bx}_{\text{np}}/(b{\gamma }_2-1),\\ {\stackrel{.}{x}}_2={bx}_{\text{np}}/(1-b{\gamma }_2).\end{array}$$ (12)

This system has the solution x = (x₁, x₂) given by

$$\begin{array}{r}{x}_1(t)={\gamma }_2(t-t_1){bx}_{\text{np}}/(b{\gamma }_2-1)+x_1(t_1)\\ x_2(t)={bx}_{\text{np}}(t-t_1)/(1-b{\gamma }_2)+x_2(t_1).\end{array}$$

Substituting these solutions into (11) and simplifying, we determine the constrained optimal CPA addition control

$$M_2^A(t)=\frac{(1-b{\gamma }_2)x_2(t_1)+(1+bt)x_{\text{np}}}{(1-b2{\gamma }_2)x_1(t_1)-b{\gamma }_2{x}_{\text{np}}t}.$$ (13)

Thus for Case (1) we have one switching time, τ, for Case (2) we have switches t₁ < t₂ < τ, and for Case (3) we have switches t₁ < t₂. With these switching times we can define the optimal controls in each scheme. For all three cases M₁(t) ≡ 0, and in Case (1–3), we have

$$\begin{array}{cccc}& \text{Case}(1)& \text{Case}(2)& \text{Case}(3)\\ M_2(t)=& \{\begin{array}{cc}{\overline{M}}_2,& t\le \tau ,\\ 0& \tau <t<t^{\ast }\end{array},& \{\begin{array}{cc}{\overline{M}}_2,& t\le t_1,\\ M_2^A(t),& t_1<t<t_2,\\ {\overline{M}}_2,& t_2<t<\tau ,\\ 0,& \tau <t<t^{\ast }\end{array},& \{\begin{array}{cc}{\overline{M}}_2,& t\le t_1,\\ M_2^A(t),& t_1<t<t_2,\\ 0,& t_2<t<t^{\ast }.\end{array}\end{array}$$ (14)

Derivation of CPA removal optimal controls with an active constraint

In the CPA removal case, we previously [6] found that at time t₁, the inequalities p₁(t₁) < 0 and p₂(t₁) < p₁(t₁)/b hold, and thus we must maximize M₁(t) and minimize M₂(t). Now, if M̄₁ is large in the sense of Lemma 1, we may set M₂ ≡ 0. Because of this we can explicitly solve system (3) for M₁(t) as above to obtain

$$M_1=\frac{x_2(1-{\gamma }_{2}b)+x_{\text{np}}}{x_1},$$ (15)

and upon back substitution, we get

$$\begin{array}{l}{\stackrel{.}{x}}_1={bx}_2{\gamma }_2,\\ {\stackrel{.}{x}}_2=-{bx}_2,\end{array}$$ (16)

which has the solution x = (x₁, x₂) where x₁(t) = −γ₂x₂(t₁)e^−bt + x₁(t₁) + γ₂x₂(t₁) and x₂(t) = x₂(t₁)e^−bt. Substituting this solution into (11) and simplifying, we define the constrained optimal CPA removal control

$$m_1^r(t)=\frac{e^{bt}{x}_{\text{np}}+x_2(t_1)-{bx}_2(t_1){\gamma }_2}{-x_2(t_1){\gamma }_2+e^{bt}(x_1(t_1)+x_2(t_1){\gamma }_2)}.$$ (17)

For Case (1) we have one switching time, τ. For Case (2) we have switches t₁ < t₂ < τ, and for Case (3) we have switches t₁ < t₂. With these switching times we can define the optimal controls in each scheme. For all three cases m₂(t) ≡ 0, and in Case (1–3), we have

$$\begin{array}{cccc}& \text{Case}(1)& \text{Case}(2)& \text{Case}(3)\\ M_1(t)=& \{\begin{array}{cc}{\overline{M}}_1,& t\le \tau ,\\ 0,& t>t\end{array},& \{\begin{array}{cc}{\overline{M}}_1,& t\le t_1,\\ M_1^r(t),& t_1<t<t_2,\\ {\overline{M}}_1,& t_2<t<\tau ,\\ 0,& t>\tau \end{array},& \{\begin{array}{cc}{\overline{M}}_1,& t\le t_1,\\ M_1^r(t),& t_1<t<t_2,\\ 0,& t>t_2.\end{array}\end{array}$$ (18)

Application of optimal control to human oocyte CPA addition

There are significant advantages to oocyte cryopreservation. It allows women who do not have a reproductive partner to preserve their unfertilized gametes. This becomes especially relevant to children or women who may undergo potentially sterilizing iatrogenic procedures such as chemotherapy [2]. Nearly 17% of couples experience fertility problems, and the use of cryopreserved embryos significantly reduces the costs associated with treatment [14]. The ethical and legal status of cryopreserved embryos, however, is a significant complication. Successful cryopreservation of oocytes would alleviate these problems and would also provide time for infectious disease screening that is not currently possible.

In the United States, the cost of all in vitro fertilization (IVF) and intracytoplasmic sperm injection (ICSI) procedures is nearly $500 million per year, but the indirect costs of the multiple live births associated with multiple embryo transfers is well over $600 million per year [9]. The social and psychological challenges of multiple gestations is also of major concern [3]. One reason multiple embryos are transfered per treatment is that ovarian stimulation and oocyte collection is an invasive and expensive procedure [2]. If oocytes could be sucessfully cryopreserved, multiple oocytes could be harvested and stored until needed, facilitating the transfer of single embryos, and avoiding the ethical problems of cryopreserving embryos and the patient problems of an invasive and expensive procedure. Transferring single embryos would reduce the overall cost of fertility treatments by half in the United States.

To date, no practical and clinically acceptable cryopreservation protocol exists for human oocytes despite these considerable advantages. Much of the failure is attributed to the sensitivity of the meiotic spindle during CPA addition and removal and while cooling from room temperature to subzero temperatures. Partly to avoid this chilling sensitivity, Kuleshova and Lopata [22] have argued that vitrification of embryos and oocytes is often favorable to equilibrium (slow) cooling techniques. O’Neil et al. [28] have demonstrated that some human oocytes can be successfully vitrified, but the required concentrations of CPA exposes cells to extreme osmotic stresses and potential chemical toxicity due to a lengthy addition and removal procedure. Specifically, to load human oocytes with 6 molar propylene glycol required for vitrification, 4 steps are needed using a standard protocol taking at least 122 minutes. On the other hand, the osmotic stress can be managed and the effects of chemical toxicity minimized by using the continuous addition protocols developed in this manuscript.

Using published parameter values for human oocytes shown in table 3, we compared optimal controls to classic controls for the addition of multimolar (6, 4.16, and 2.46 molar) propylene glycol, with results shown in table 4. Calculations were made with the assumption that the maximal external CPA concentration was 6.5 molar, corresponding to M₂ = 41, and a final concentration difference at the highest $x_2^f$ of only 0.5 molar. This value was chosen because at higher concentrations the viscosity of the solution may make the precise control of the extracellular CPA concentration impossible. The impact of this concentration constraint can be seen by the relative improvements at each goal concentration level. At the highest goal concentration the improvement ratio values range from 4.7 to 11.1, whereas at the lower concentrations the lowest time improvement is 6.5 and the greatest is 19. Nevertheless, even when ${\overline{M}}_2-x_2^f/x_1^f$ is small, the time improvements are at least five-fold.

Table 3.

Definition of parameters for oocyte propylene glycol addition

Published and defined parametersa
Parameter	Name	Value (at 22 °C)
Lp	Hydraulic Conductivity b	0.53 μm min−1 atm−1
Ps	Solute permeability	16.68 μm min−1
Vi	Initial volume in isosmotic media	2,650,000 μm3
Vb	Osmotically Inactive Volume	503,500 μm3
$V_w^i$	Isosmotic water volume ( $V_w^i=V^i-V_b$)	2,146,500 μm3
$V_w^f$	Desired final water volume	2,146,500 μm3
A	Cell surface area based on sphere of volume Vi	92,539 μm2
V*	Lower volume constraint	0.7 × Vi
T	Temperature	295.15 K
R	Gas Constant	0.08205 L atm K−1 mol−1
Miso	Isosmotic molarity	0.29 mol/L
$c_s^i$	initial intracellular permeating solute concentration	0 mol/L
$c_s^f$	final intracellular permeating solute concentration	3 mol/L

Calculated (unitless) parameters
Parameter	Equation	Calculated value
b	Ps/LpRTMiso	4.48
$x_1^i$	$V_w^i/V_w^i$	1
$x_2^i$	$x_1^i{c}_s^i/M^{\mathit{iso}}$	0
$x_1^f$	$V_w^f/V_w^i$	1
$x_2^f$	$x_1^f{c}_s^f/M^{\mathit{iso}}$	10.34
k*	$V_{\ast }-V_b/V_w^i$	0.51

^aAll values from [29] unless noted.

^bWater and solute permeability values published in the literature were determined using a different flux model. To account for this, the conversion was made in a similar manner to that described in [8].

Table 4.

Comparison of multimolal CPA addition equilibration times for human oocytes. Several standard protocols with total unitless time t^t, are compared with the optimal constrained protocol. Real times are calculated by multiplying unitless times by $L_p{\mathit{ARTM}}^{\mathit{iso}}/V_w^i=A/V_w^i{P}_{s}b=0.234$. The maximal permeating solute concentration was chosen to be 41, corresponding a 6.5 molar concentration of PG^a. CPA addition equilibrium steps were determined by calculating the smallest CPA concentration $M_2^{\ast }$ such that x₁ +γ₂x₂ = k_*, and then following the solution until the switch time equation was satisfied, at which point a new $M_2^{\ast }$ was calculated.

$x_2^f$	switch time equation	tt	tt/t*	actual equilibration time (min)	equilibration steps
36	$x_1(t)=0.99x_1^i$	522.6	11.12	122.	4
	$x_1(t)=0.95x_1^i$	281.2	5.98	65.8	4
	$x_1(t)=0.90x_1^i$	220.2	4.69	51.5	5
20	$x_1(t)=0.99x_1^i$	374.9	19.4	87.7	4
	$x_1(t)=0.95x_1^i$	197.3	10.2	46.2	4
	$x_1(t)=0.90x_1^i$	128.8	6.7	30.1	4
10	$x_1(t)=0.99x_1^i$	174.9	18.08	40.9	3
	$x_1(t)=0.95x_1^i$	94.5	9.76	22.1	3
	$x_1(t)=0.90x_1^i$	62.5	6.45	14.6	3

^aThis is about a 44% mass-fraction solution

Sensitivity to parameters

In a biological system with several measured parameters, there will be considerable variation in parameters from one population and even one individual to another. Therefore the implementation of a closed loop optimal control is bound to be subject to errors induced by these variations. We are interested, then, in the effects of these variations on particular endpoints in this protocol, namely, the switching and total times. Additionally, one would expect that there would be cell-to-cell variability in the state constraint as well. This type of problem is easier to “engineer” around: one may simply choose a stricter constraint from the outset, but we wish to know the effects of moving the state-constraint location on the total transit time.

In the interest of brevity, we will only treat the CPA addition case in which the optimal control follows case (3) of equation (14). Although an analytic expression for the total transit time can be found up to fourth order error terms, this complicated expression involves multiple special functions, and thus is impractical to use for sensitivity analysis. Therefore we will provide a numerical analysis of the sensitivity to the parameters b, k_*, and M̄₂.

The percent error of total time, fixing 1 of the 3 parameters for the respective initial and endpoints xⁱ = (1,0) and x^f = (1,1) is shown in figure 3. “Correct” parameter values were assumed to be (b, k_*, M̄₂) = (0.8, 0.8, 5.8). The plots are divided into three regions corresponding to the three possible cases, zero, one or two intersections of optimal trajectory with the state constraint. The region contained inside the dashed line corresponds to the case (2) from system (14), the region above and to the right corresponds to case (3) and the region below and to the left corresponds to case (1). For cases (1) and (3) there is a significant effect of maximum concentration, as expected, but for case (2) there is almost no influence of the maximum concentration on the total transit time. This is because the total time to and from the state constraint are small and the total time along the state constratint does not depend explicitly on M̄₂.

Fig. 3.

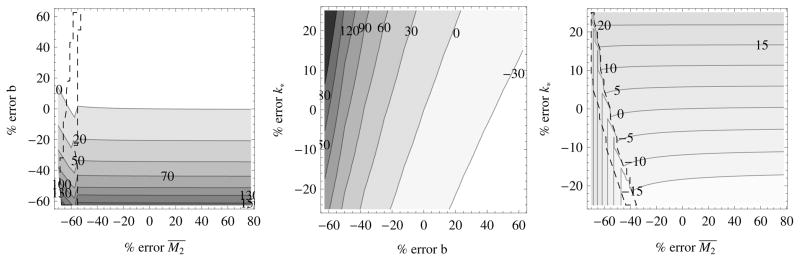
numerical sensitivity analysis plots. the dashed lines surround the values corresponding to case (2) from display (14). in the case (3) scheme, the error is relatively insensitive to m̄₂, but is sensitive to both b and k_*.

Discussion and conclusions

Theoretical optimization of cryobiological protocols allows for critical engineering and biological decisions to be made that account for parameter uncertainties in individual cell populations along with imperfect controls. The predictions of this model, with specific, but quite typical parameter values indicate that a significant improvement on the order of 10–20 fold over current techniques is achievable. To put this in perspective, current deglycerolization techniques require 25–30 minutes for the complete process [1]. Using our proposed methods, this protocol should take less than 5 minutes, if optimal controls can be achieved. Unfortunately, accurate estimates of both water and glycerol permeabilities at the wide range of concentrations needed for blood deglycerolization have not been made.

This technique also may be applied to cell types for which standard equilibrium freezing approaches are not sufficient: if extremely high concentrations of CPAs can be equlibrated within the cells, then ultrarapid cooling may “vitrify” both the cells and their surrounding media, achieving a stable amorphous glass. A distinct advantage of this technique is that any x^f may be specified, allowing the control of the amount of dehydration in the final state, yielding even better glass forming tendencies.

In general, even for a large range of temperatures and cell types, 10⁻¹ ≤ b ≤ 10¹ and 0.5 ≤ k_* ≤ 0.9 [4,8]. Because the current “state of the art optimal” CPA addition and removal protocol depends on step-wise (e.g. M₁ and M₂ piecewise constant) protocols, we may compare standard approches to the approach outlined in this manuscript over a very large range of cell types and temperatures. One significant detriment of the traditional approaches is that these produce multiple osmotic events which may have a cumulative damaging effect, but moreover, are difficult to implement as standard laboratory procedures. In Table 5 we show the relative time improvement of the new protocols over “traditional” protocols, along with the expected step count for the standard approach for each combination of parameters.

Table 5.

Relative time improvement of the optimized protocols (with total time t^*) over standard protocols (with total time t^t) for a range of unitless parameters and both CPA addition and removal schemes. The number of required equilibrium (standard) steps is also given. In the CPA addition case, $x_2^f=10$ and in the CPA removal case $x_2^i=10$. Characteristic maximal concentrations M̄₁ and M̄₂ were both chosen to be 20. CPA addition equilibrium steps Σ were determined by calculating the smallest CPA concentration $M_2^{\ast }$ such that x₁ + γ₂x₂ = k_*, and then following the solution until $x_1=0.95x_1^i$, at which point a new $M_2^{\ast }$ was calculated. CPA removal equilibrium steps were determined by calculating the largest CPA concentration $M_2^{\ast }$ such that x₁ + γ₂x₂ = k^*, and then following the solution until $x_1=1.03x_1^i$, at which point a new $M_2^{\ast }$ was calculated, except for the last step, when the solution was followed until $x_1=1.01x_1^i$. Note that for CPA removal, the optimal transit time does not depend on k^*.

Addition of CPA, $x_2^f=10$						Removal of CPA, $x_2^i=10$
b	k*	tt	t*	tt/t*	Σ	b	k*	k*	tt	t*	tt/t*	Σ
0.1	0.9	859	79.0	10.9	21	0.1	0.7	1.3	1100	30.0	36.7	17
0.1	0.7	492	59.0	8.33	6	0.1	0.7	1.5	713	30.0	23.7	8
0.1	0.5	399	39.0	10.24	4	0.1	0.7	1.7	569	30.0	18.9	5
1	0.9	84.5	7.86	10.8	14	1	0.7	1.3	107.	3.07	34.9	13
1	0.7	46.5	5.83	7.98	4	1	0.7	1.5	69.9	3.07	22.8	6
1	0.5	40.9	3.80	10.8	3	1	0.7	1.7	55.5	3.07	18.1	4

This manuscript provides a blueprint for the optimization of cryopreservation protocols, but makes several critical assumptions that must be investigated before implementation in a real-world sense. First, we used an ideal-dilute solution model to facilitate the analytic solution of the optimal control problems. Though mathematically elegant, this assumption may not provide enough accuracy for solutions ranging above 2–3 molal concentrations. Because of this one may have to choose a suitable non-ideal model for high concentration protocol definition, for example, a simple model that captures much of the non-ideality is one defined by Elliott et al. [11]. Optimal control of systems of this nature is a current area of our research.

Additionally, this protocol depends on the accurate control of the extracellular envirionment immediately adjacent to the cell membrane. In order to implement this control, the extracellular media must be continuously controlled, perhaps by either flowing media over a cell fixed by pipette or membrane [12,27], or by moving the cell through a counter-current, dialysis device [10]. Under both of these conditions, achieving accurate control at the cell membrane boundary involves significant mathematical and engineering effort, with the complications of nonlinear advection and diffusion along with changing viscosities affecting unstirred and boundary layers. These questions were at least partially addressed by Benson [4], with results indicating that at single somatic cell sizes, as long as the membrane surface area remains free, diffusion is sufficient to overcome advective effects, and an ordinary differential equation is most likely sufficient.