Table 2. Table of Lagrangian terms, in terms of current.

parameter	phasor	Lagrangian	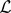order, k	Euler-Lagrange
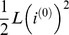
inductance, L	I  =  (−j/(ωL)) V		0	+ Li (0)
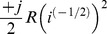
resistance, R	I  =  (1/R) V		−1/2	+ Ri (−1)
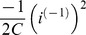
capacitance, C	I  =  (+jωC) V		−1

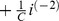
Lagrangian terms, with current: We list the common electrical lumped parameters, and compare the admittance with the corresponding term from the Lagrangian function. We also list the order of differentiation, k, and the corresponding term from the Euler-Lagrange equation. The phase direction of the Lagrangian term leads the phase direction of the admittance by 90°. This is equivalent to multiplying the Lagrangian term by +j. We can multiply the Lagrangian term by any constant that we like, as long as we do this consistently. If we were to remove the factor of +j then the Lagrangian terms and the admittances will have consistent phases, but all the Lagrangians will have new phases, and some of these will not be consistent with existing practice in mechanics. In this paper, we rigorously adopt the convention that is used in mechanics, which means that we do not use the sign convention that is common in electrical engineering.