What Type of Person Are You? Old-Fashioned Thinking Even in Modern Science

Abstract

People around the world have folk origin myths, stories that explain where they came from and account for their place in the world and their differences from other peoples. As scientists, however, we claim to be seeking literal historical truth. In Western culture, typological ideas about human variation are at least as ancient as written discussion of the subject, and have dominated both social and scientific thinking about race. From Herodotus to the Biblical lost tribes of Israel, and surprisingly even to today, it has been common to view our species as composed of distinct, or even discrete groups, types, or “races,” with other individuals admixed from among those groups. Such rhetoric goes so much against the well-known evolutionary realities that it must reflect something deep about human thought, at least in Western culture. Typological approaches can be convenient for some pragmatic aspects of scientific analysis, but they can be seductively deceiving. We know how to think differently and should do so, given the historical abuses that have occurred as a result of typological thinking that seem always to lurk in the human heart.

We commonly view our own species as composed of distinct types, or “races.” But human variation is more graded; evolution is a population process that occurs gradually over eons of time.

Every naturalist who has had the misfortune to undertake the description of a group of highly varying organisms, has encountered cases (I speak after experience) precisely like that of man; and if of a cautious disposition, he will end by uniting all the forms which graduate into each other, under a single species; for he will say to himself that he has no right to give names to objects which he cannot define.

—Charles Darwin Descent of Man, 1871

Do races exist? We often hear scientists, pundits, and even just ordinary people debate this question, usually contentiously, and collections (such as this one) are published to try to answer it. But the answer is clear and very simple, and it is: yes, races exist!

There can be no doubt about this. Too many people use the word routinely, and this by itself gives the term, and their lives, some existential meaning, and by default some sort of empirical meaning as well because it can affect where and how they live. Yet the variation in the word’s usage makes it equally clear that the concept of “race” exists separately in the mind of each beholder. The legitimate scientific issue is the meaning and utility of the term in human biology.

Why do we still need repeated iterations of angst-laden discussions about what, or even if, “race” is? The relevant facts were known at the origins of modern scientific treatments of this subject, with caveats and clear statements made repeatedly ever since (e.g., see Kittles and Weiss 2003; Weiss and Fullerton 2006), including Darwin’s own famous statement, given in our introductory quote. The persistence of the issue suggests that there are no experts who can enlighten us, with any finality, which suggests that this is not a matter of epistemological expertise. The reasons have little to do with the underlying biology: The reasons are cultural. However, they also entail concepts of human history and that is a subject to which one might expect that genetics could contribute in some definitive way. Indeed, the history of those concepts of history themselves is informative and worth a brief summary.

A BIT OF HISTORY

Not so long ago, it was not at all clear that the living world had much of a history. Species, as scientists, scholars, and the ordinary person knew them, had been around, essentially unchanged, since the earliest recorded writings. A set of instantly created species was the Biblical explanation (in the West, at least), because, after all, how else could oats, goats, whales, and snails have gotten here? Although here and there one can find alternative speculations, the panoply of Nature’s species seemed, from the ancients to the 19th century, to constitute a complete fabric of the possible and useful existence, with a hierarchy of types of animals and plants, from simple to complex with humans at the top, the pinnacle of existence. These types were widely seen as permanent and essentially unchanging categories of nature, God’s wisely constructed spectrum that came to be called the Great Chain of Being (Lovejoy 1936). In this context, in the middle 1700s, Carl Linnaeus developed a system of classifying living organisms that we still use today.

The major transformation in thinking was the development of a scientific rather than religious explanation for the origin of species, which Darwin referred to as the “mystery of mysteries.” The genius of Darwin and Alfred Wallace (and a few precursors) was to see that the same variety of types of beings could be generated by historical “processes” alone, without the need for discrete “events” of spontaneous generation or divine creation. The process was the gradual one that we call “evolution.” In essence, types led to other types by gradual changes over eons of time, and all types that are here today resulted from that process operating since, and everything descended from a single origin of life on earth. That challenged religious comforts, but provided the ability to understand the world in scientific terms.

The concept of natural types is closely connected historically to the notion of a “type specimen,” assumed to be representative of their kind, and museums were staffed (and stuffed) with them. Even well after Darwin, however, there was discussion of what constituted a type and how many individuals, or which individuals, were needed to define one (e.g., Schuchert 1897). Type specimens are distinct discrete entities, taken as representative because everyone has known that variation is the essential key to evolution. In his studies of barnacles, an 8-year drudgery that he undertook in part to build support in his own mind for his theory of evolution, Darwin observed that every part of every species varied. He bemoaned that “Systematic work would be easy were it not for this confounded variation” (Darwin 1850). That must be the case if adaptive evolution were to occur, because evolution requires variation, which is in turn necessary for populations to split into other populations that over time become reproductively isolated—and become new species. This, in its turn, challenged the idea of the static fixity of species on which pre-evolutionary ideas rested and that motivated Darwin’s innovative thinking. And there is no hierarchy in this process; bacteria are still here and doing very well after 3.5 billion years! Darwin showed that the appearance of species stasis was an illusion due to the glacially slow changes that evolution wrought.

OUR PLACE IN NATURE

In subtle ways, even scientists, who know better, as well as the general public, still indulge in careless typological thinking about humans as well as other species. Western culture has conflated concepts of type and race for obvious reasons that we might call historical. Races as natural types were inferred in pre-Darwinian times as God’s separate creations, and although they were interfertile they were considered equivalent to subspecies. Even well into the 20th century, descriptive rhetoric often has taken such forms as “the Caucasian has a broader head than the Negro …” or a more euphemistic version “Europeans have ….” This is not really different from how we refer to the mouse, horse, or snapdragon.

Darwin’s quote shows that it was well recognized even then that whatever these human “types” were, they were not really fixed types. Yet, great effort has been made to identify the human types by generations of anthropologists who professed to be evolutionists, even after stating the brief caveat that variation is quantitative and overlapping, the caveat immediately thereafter honored in the typological breach.

The most important point is that if one is determined to identify human types in the real, rather than Platonic ideal sense, one must assume that they actually exist to obtain specimens of them. In a kind of circular logic, the belief in the existence of races places a statistical bias or prior probability on the number or identity of races, assumed to be real ontological entities, which samples collected on that basis are then used to reinforce. We do that by prejudging the question and, for example, by sampling from discrete locales (populations, languages, ethnicities, etc.). In other words, to assess the variation between populations, we have to identify them, often by name (“Europeans,” “Asians,” “Nigerians”), which itself then determines the samples that are collected. One can always find statistical differences between any kinds of samples, and there are certainly practical issues involved in sample choice for anthropology and genetics, but sampling from preidentified populations almost enforces categorical interpretation, as if the sample choice were dictated by the categories. But sample choice is subjective, and if we force it into our assumed conceptions, we can make the statistical shoe fit. This is especially problematic when the objective extends beyond categorical treatment of present populations to using such concepts to reconstruct individual genetic ancestry.

ANCESTRY TESTING AS TYPOLOGICAL THINKING

Genetic ancestry testing has become a boom business. It is marketed as popular recreation, supported by appealing television documentaries, and widely used in science as well. It appears to be positively viewed by those who used, or who would use, these services (Wagner and Weiss 2012). Besides the fun of getting an idea of who one’s ancestors were, ancestry estimation can have epidemiological relevance. Genetic ancestry testing uses an individual’s genotype (variant nucleotides in his/her DNA sequence) to estimate the fractions of that genotype that was derived historically from a set of putative “ancestral” or “parental” populations, usually referring to geographic regions, whose frequencies of a set of tested alleles (genetic variants) are known. Often, although the word itself may not be used, these regions correspond to the homelands of the classically denoted human races. The test individual is said to be the “admixed” descendant from those populations.

Besides ancestry estimation of individuals requesting the service, admixture-based concepts are also routinely used to describe the ancestral history of samples of multiple individuals from present-day populations, such as U.S. African-Americans (Shriver and Kittles 2004), Hispanics and Native Americans (Wang et al. 2007, 2008; Bryc et al. 2010), Africans (Tishkoff et al. 2009), Europeans (Bauchet et al. 2007; Novembre et al. 2008), and South Asians (Reich et al. 2009). Indeed, variation in our entire species has been analyzed in this way (Rosenberg et al. 2002; Li et al. 2008).

Admixture approaches to human biological diversity take as an assumption the reality of the parental populations; that is, it is assumed that there are, or were, such “pure” human populations, and that everyone is either a member of such a group, or is admixed from them. Historical parentals are assumed to be represented accurately by sampling some current population. In this way, whether or not the term “race” itself is used, prominent and sophisticated analysis of population history continues to be based fundamentally on racial (although not racist) assumptions. But if parental populations actually exist (or existed), we must identify them somehow, decide where and how many they are (or were), and explain how individuals can be assigned ancestry from them. That turns out not to be so easy.

STATISTICAL DEFINITIONS OF POPULATION AND TYPE

We should clarify what we mean by a population, whether it is admixed or not. Otherwise, the word can carelessly be used as a euphemism for “type,” which can mislead one into thinking that a population is a collection of individuals all of the same “type” and isolated from other such collections. Instead, in the admixture estimation context, population is a different and rather subtle kind of type.

A typical definition of such a population is a collection of individuals who choose their mates randomly from among others within the population, but not from other populations. Extending this idea, an admixed population is one that was formed by contributions from two or more such “parental” (donor) populations, but that at the time of observation has random mating internally.

The idea of random mate choice may seem strange to readers not familiar with the genetics of populations, but one should not worry about that because the concept is an effective working simplification, which essentially just means that mates are chosen from within the population without regard to the choice’s particular genotype. That this is not literally true can cause some problems, as we will see, but for the moment it does not affect the points we wish to make.

The view of humans as being members of self-contained populations is, however, rather strange because neither the facts nor theory provide support for the idea of rigid population boundaries in the process by which actual human variation has been generated and distributed around the Earth. Traits such as language and religion have always posed some local restrictions on mating, but by no means were they complete nor did they lead to truly closed, random-making populations. In this sense, the common approaches that invoke discrete ancestral populations, although couched in evolutionary terms, are basically non-Darwinian (Weiss and Long 2009). Decades of anthropology have shown that populations exchange mates often through mandatory village exogamy in which mates must be chosen from members of some group other than one’s own. Even geographic barriers are typically not complete (except perhaps some truly isolated and relatively recent habitation of mountain valleys, Pacific islands, etc.).

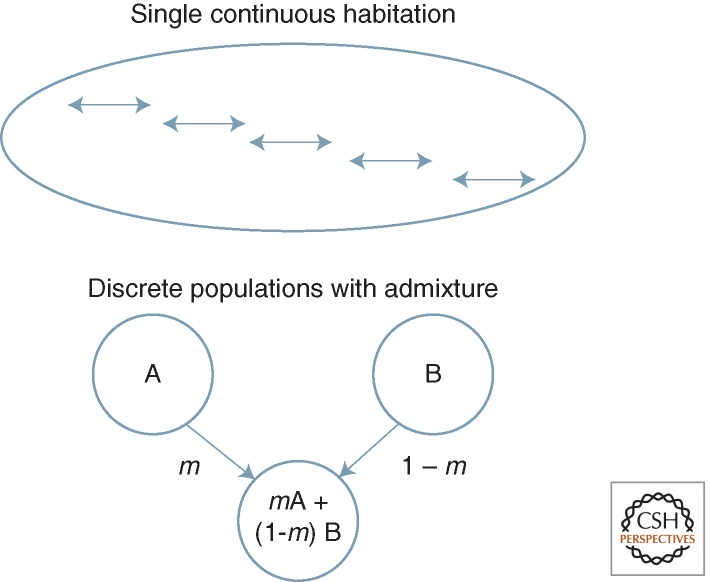
Admixture-based analysis uses a particular kind of typology that recognizes that members of a “pure” population, like A and B in Figure 1, are not clones; their individuals vary. What is actually suggested, if only implicitly, is a “statistical typology,” in which the population is in random-mating proportions for the frequencies of alleles in the population, at a set of sites to be examined. If different members of a population have different nucleotides (A, C, G, or T) at a given position, an individual’s genotype at that site is the pair of alleles that s/he carries at that site. In a random-mating population, each individual draws its genotypes from the same set of possibilities—the allele frequencies for each of the varying sites to be considered. For example, suppose we consider a site with two nucleotides present in the population, say, 20% A and 80% G. If there is random mating, the chance someone is AA is 16% (20% for the person’s first copy and, again, 20% for its second). A similar story would apply to every other varying site, applying that site’s allele frequencies to the probability that the individual had each of its possible genotypes, and so on across the genome. For readers familiar with the term, the population is in Hardy-Weinberg equilibrium for the respective allele frequencies.

Figure 1.

Populations and admixed populations. (Top) The human population as a quasi-continuous range based on serial expansion from a single source. (Bottom) A population formed by a fraction, m, of immigrants from discrete population A and the remainder from population B (for description, see text).

What constitutes a population in the current sense is that the variation among its members is in these random-mating proportions. These are the statistical “types” that comprise the population; the “type” is, in a sense, the set of allele frequencies from which each member’s unique genotype was produced.

Individuals in an admixed population are treated as having drawn their genotypes as random samples of alleles from the respective allele-frequency sets of their contributing parental populations, weighted by the proportion of admixture (e.g., m in Fig. 1). In the admixed population, the genotypes are also due to random mating, but with these admixture-weighted allele frequencies. The effect of admixture is similar to mixing paint of different colors. The relative amounts of red and white paint that formed some new mixed paint would determine its shade of pink.

Something about these ideas might seem strange, and it is important to be aware of them. Genotyping in an admixture-based analysis is typically restricted to globally varying sites, that is, sites in which the same alleles are found in many or even all of the parental populations, although their allele frequencies may vary among the populations. This means that by the very assumptions of admixture analysis it is possible for people in any of the parental populations to have precisely the same genotype, yet those populations are treated as different “types!”

It may seem curious to define distinct parental populations in terms of alleles they all share, but it is pragmatically important. Each newborn person, no matter where, inherits new mutational variants that are not found anywhere else. It is not very helpful to use such variants in comparing groups, and indeed one else in the same group has a new variant. Similar uselessness applies to variants that are quite rare in any group. The poet John Donne said that no man is an island, but if one only used each man’s unique alleles it would be much more difficult to identify groups; the concept of variant frequency would lose much of its meaning, as would the genetic concept of population itself. We are, thus, constrained to compare group differences by things whose variation is shared among the groups. And, once we have a sample divided into such populations, or sets of statistical types, despite the fact that in principle any genotype could be found in any population, if we look at enough sites we can always assign an individual to his/her respective population. This is a curious result of combining many different probabilities (from the array of tested sites in the genome). Although it is possible for any given genotype to arise in any population, if enough sites are considered the probability of that person’s genotype arising in any population other than his/her own becomes miniscule.

This kind of admixture-based analysis was initially developed at least in part not for direct investigations of true population history in the ancestry sense, but to detect structure within samples used for gene-mapping studies to reduce false-positive associations between single-nucleotide polymorphism (SNPs) and diseases. Substructure within a population can lead to such results, suggesting that some place in the genome contributes to the disease, which can mislead follow-up clinical research. For example, a subgroup might share a disease and also (by chance) some genetic variant that has nothing to do with the disease, but the association between the two could look like causation if the existence of the subgroup was not taken into account.

For this reason, the admixture approach is now often called a “structure” analysis after the name of the first modern computer analysis program that was based on this approach (Pritchard et al. 2000), of which there are now others (e.g., Tang et al. 2005a; admixmap.sourceforge.net). Because even within local villages, humans do not literally choose mates at random, random mating is a pragmatic statistical concept rather than one that attempts to address actual history, and more fine-grained analysis shows that populations treated as homogeneous at one level of resolution have comparable internal diversity at more local levels of resolution (Novembre et al. 2008; Wang et al. 2008; Weiss 2010). But the fact that a population’s internal admixture structure depends on how closely you choose to examine it, casts questions about the historical validity and applicability of the approach.

It is important to note that categorical treatment of human variation, including implicit statistical race definitions, is not new (Kittles and Weiss 2003; Weiss and Fullerton 2006; Weiss and Long 2009; Weiss 2010). Because of their sorry historical abuse, words like “pure” and “race” are not commonly used by scientists today. But euphemistic terms like “ethnic group” are, and if we are aware of the problems then why are we doing the same kind of conceptual analysis after a 150-year history of evolutionary reasons to know better?

FITTING A SQUARE CONCEPT INTO A ROUND REALITY

How does a categorical view square with the observed ubiquitous, more or less continuous, human geographic variation? By the 20th century, more modern concepts than classical Linnaean static types were available and attempts were made to fit a discrete typology into a more continuous whole. For example, the leading physical anthropologist, E.A. Hooton, published a sober discussion in Science in 1926 on methods for analyzing races (Hooton 1926) that exemplifies this type, so to speak, of thinking. Hooton said that to characterize human races in modern scientific terms, one must metrically analyze collections of (say) skeletons, first grouping them into clear sets (by using expert judgment!). Then, he argued, with the multivariate techniques of the time, the patterns of variation within and between groups could be discerned quantitatively; pure races will be “very apparent.” These are the product of “evolutionary factors,” he wrote, and with this as a basis one can use metric techniques to identify the “composite” nature of other groups produced by intermixture among these primary races. Here, we have what seems on the surface to be a modern, Darwinian, process-based way to consider types.

Hooton was a physical anthropologist, but he was writing at the dawn of genetics, and geneticists jumped into the fray to modernize this subject (or, as they would proclaim, to make it more rigorous). Because genes are taken as the fundamental causal units of life and evolution, it seemed to some that races should be defined by sets of clearly Mendelian traits (that is, that are each inherited as if because of variation in a single gene) rather than much “softer” morphometric data that may be affected by environments (Mendelian segregation of phenotypes was the criterion for genetic causation at that time when specific underlying genes were not known). This was the approach taken by the globally leading textbook in human genetics (Baur et al. 1931).

Baur et al. (1931) argued that races defined in this way are “sharply delimited” and “there are only men and women belonging to particular races or particular racial crossings.” It is more than incidental that this book was squarely within the eugenics era, and viewed racial traits as the product of Darwinian selection. The Darwinian perspective initially led to discrimination against individuals deemed by physicians to be inherently deficient. But in a typological age, it was easy to extend the same ideas to value judgments about inherent characteristics of groups, and such ideas provided a feeder justification for the Nazis. The history of eugenic abuses is beyond our scope here, but the issues have been reviewed elsewhere (Kevles 1995; Carlson 2001; Weiss and Lambert 2010; and see articles in the May 2011 Ann Hum Genet, Vol. 75, No. 3).

All the eugenic-era investigators were well, indeed explicitly, aware of variation within their “types” to the point that no two non-twin members of the same type were identical. A subtle innuendo was that this variation did not overlap between groups in any substantial way, but this clearly is not true if the alleles are, by choice, present in different groups. Clearly as well, results were then (and remain today) dependent on the samples chosen for study. If one only samples Europeans and Asians to define one’s races, their chosen traits might not overlap with, say, Indians, who could then be viewed as admixed between Europeans and Asians. But if one were to choose Africans and Europeans as parent populations, Asians could be viewed as their admixed descendants.

Nonetheless, and if we can blinker ourselves to overlook the abuses that took place in the name of such thinking, and its misappropriation of Darwin’s name, we can see the sleight of hand that is involved. What we have is a definition of a round peg in a square hole: a variable type.

As described above, in population genetic terms, a variable type (a statistical “race”) is defined as a population whose individuals were formed by randomly drawing variants twice from each test location in the genome. And also as described above, this is what the admixture-based approaches do as well, given the estimated mixing population proportions. In the admixed case, this means that each individual can by chance have drawn somewhat more, or fewer, variants that had come originally from a given source population.

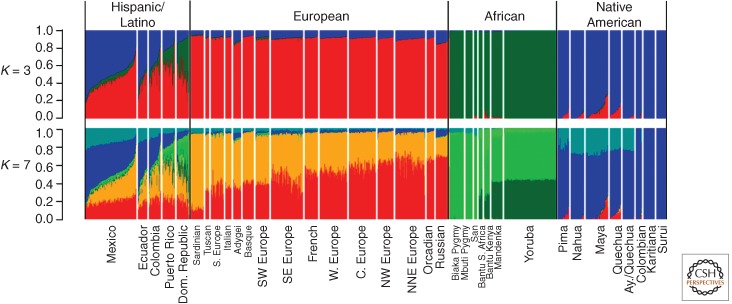
Figure 2 shows a common graphical portrayal of an admixture-analysis result, in which sampled individuals are arrayed along a linear axis, grouped according to the sample from which each individual was obtained; the groups usually arrayed in geographical order, such as from west to east. The analytic software identifies (or is asked to identify) a number of ancestral (“parental”) populations, each of which is given a color code. Then every sampled individual is plotted as a thin vertical bar, with color-coded segments corresponding to the parental populations and of length proportional to the estimated fraction of the individual’s ancestry from that parental population.

Figure 2.

An admixture-structure presentation of a global sample of human genetic variation. Ancestry fraction scale is on the left. The top bar assumes three ancestral populations (K = 3), of which all individuals are members or admixed descendants, whereas the bottom panel is the same if seven (K = 7) ancestrals are assumed. (From Bryc et al. 2010; in the public domain.)

In the resulting figures, geographic proximity is clearly reflected by the similarities of admixture patterns in individuals sampled from the same or nearby geographic regions (these individuals are thus adjacent or near to each other along the plot). If the number, K, of random-mating parental populations is to be estimated by the program rather than prespecified by the investigator, the number of parental populations becomes a matter of judging the statistical results, and the investigators choose what seems to be the best number (papers usually present results from various tested K-values, specifying which they feel is best). The typical global- or continent-scale study presents values between K = 5 and 15. For some individuals, the program assigns virtually all of their ancestry to a single parental population, essentially meaning that their genotypes are “pure” representatives of that population. But most individuals are estimated as having ancestry from two, or even more parental population sources.

This is clearly a literal fiction because the sampled individuals are all contemporary, may live very far apart, and each person can have only two immediate parents. In this sense, the admixture methods confound direct genealogical with population-historic concepts because the evidence must reflect earlier generations of contribution. There is no surprise in that, but it does imply that the contemporary sample interpretably represents assumed ancestral parental populations that really did exist as such. This assumption entails vague mixing concepts, imposing boundaries based on current data, and/or on populations assumed to have existed as discrete evolutionary units at some unspecified point in the past. Because the sampled individuals live geographically very far apart, the gene flow that is assumed must have had at least some historical depth, implicitly extending the assumptions about the long-standing purity of the parentals. The depth of history being reflected in this kind of analysis is rarely stated, indeed, would be very problematic to state convincingly, because it depends on the samples chosen and how they are interpreted. African Americans, for example, have some African and some European (and possibly other) ancestry, but that could have come from various places in the different continents and one or some unknown number of times in the 500 years since Columbus “discovered” the Americas (or by pre-Columbian European/African contacts).

Because to do this kind of analysis one must define the populations and the sampling frame, the analysis is often dangerously close to circular or self-affirming. It is, of course, easy to identify groups for sampling by language, political unit, nation, or because some anthropologist decided to live there for a while and gave them a name. Thus, in Figure 2, if there are assumed to be only three global contributing populations, the admixture pattern in each individual becomes simpler than if one assumes seven parental populations, but of course there has been only one actual human population history.

How these criteria reflect real history as well as the analysis itself may vary with the software program used in the admixture analysis, and each program has its own assumptions and methods, which can affect the results. For example, the investigators of the original modern admixture program called STRUCTURE (Pritchard et al. 2000) clearly provide all of the appropriate caveats, in clear terms, and most importantly the subjective judgments required in interpretation and that the program is designed to estimate admixture history even when admixture is an appropriate way to view what actually happened (if that is even known).

The presence of such cautions does not imply they are heeded or clearly acknowledged in the papers reporting use of the programs. Admixture analysis makes nice stories, although we know they are fairy tales, and the availability of convenient statistical programs does not justify users of such programs to present results that are manifestly misleading. For example, if one restricts one’s geographic attention and looks close-up within a putative parental population by subsampling in its home region, one finds similarly rich internal admixture structure (structure in the same sense and revealed by the same kind of analysis) as was found in the larger geographic area. Figure 3 shows this clearly with regard to Europe relative to Europeans considered in the global context in Figure 2; such intraregional heterogeneity is, of course, widely recognized even by the proverbial man in the street. Note that in Figure 2 we presented results comparing whether K = 3 or 7 global parental populations were assumed, but Figure 3 is based on six parental populations in Europe alone.

Figure 3.

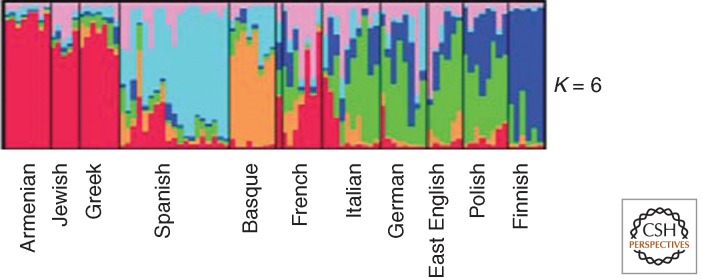
A geographic close up of one region, Europe, covered in Figure 1. (From Bauchet et al. 2007; reprinted, with permission, © Elsevier.)

As noted earlier, this yields the somewhat strange idea that a population’s “purity” depends on how closely the beholder looks at it. Perhaps when one has acne, close looks are not welcome, but in science they should be consistent with the interpretations being explicitly or implicitly given. Statistically, deviations from random mating among local subregions are small relative to the same differences in the context of a broader geographic sampling, as we would expect. However, either a population is “pure” in this sense or it is not, and such scale-dependence of the structure of populations is not exactly what people have in mind about “races” or types.

Now, if the measure used to define races is based on globally shared and, hence, relatively common allelic polymorphisms as is usually performed, then what we have is that a race is a polygenic statistical population. Indeed, globally common SNPs are perforce ancient and antedate the distinct types they are used to define. Further, a statistical definition implies that races are only quantitatively rather than qualitatively different, that is, they are not actual “types” because as mentioned earlier their definition allows each multisite genotype potentially to be found in any race.

This leads to a conundrum because if only nonshared variants were studied instead, one might think that groups could be identified once a sample was taken and thus could be used to define each race tautologically as a distinct type; it is a distinct type because it has distinct alleles. However, most nonshared variants will only be found in some individuals in a purported race’s geographic homeland. That might seem to imply rather strangely that, depending on how definitions are operationalized, members of a purported race would not have all of its defining alleles! This shows how what one chooses to sample can affect or even predetermine the results. That is not supposed to happen in science.

Despite or, often we think, oblivious to these issues, the admixture-structure approach is nonetheless now routinely used in anthropological genetics, as exemplified by Figures 2 and 3 (Weiss and Long 2009; Weiss 2010; Weiss and Lambert 2010). Investigators are usually careful not to use words like “race,” perhaps for political correctness, but the groupings are similar to classical races, and the ideas are the same in terms of the analysis used, disclaimers notwithstanding. This is clearly what one would expect of geographic samples of distantly located populations when the true generating process was basically an expansion for a human source population in Africa by gradual expansion of the leading edge of human population northward and eastward into Europe and Asia, a process that is not “admixture” between people from internally homogeneous, much less distant populations.

The availability of convenient statistical programs does not justify science that is knowingly misleading.

From an evolutionary point of view, what admixture analysis does is essentially to identify the historically and topographically induced irregularities in the otherwise roughly gradual pattern of change in genetic variation over geographic space, and it recognizes the increasing differences in peoples living farther apart. That is a true reflection of history as a process, except to the extent that it is colored, knowingly or otherwise, by selective de facto typological sampling and the assumption of statistically homogeneous source populations.

We can see the basic problem by reference to Figure 4, which imposes concepts of admixture seen in Figure 1 as they are now routinely used in structure analysis on the landscape produced by actual history. This shows what happens if a counterfactual assumption of admixture (as if it were like the lower panel of Fig. 1) is imposed on the reality panel (top): the dotted circles show how samples chosen from different parts of this actual continuity and treated as if they were isolated discrete or closed parental populations, who donated to samples from in between them. The result will be seen as an admixture result, simply because it is assumed to be that way.

Figure 4.

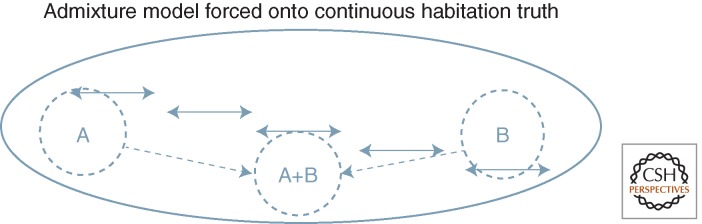
Admixture analysis can be imposed counterfactually on a continuous reality. Based on images from Figure 1, with, K = 2 parental populations, the middle population is analyzed as if it were a true admixed product of discrete populations A and B, which it is not (see text).

SIMULATION ILLUSTRATES THE POINTS

One way to illustrate these points is to use a computer to simulate populations and their history in a reasonably realistic way, and then to examine the results as they are, and as they might appear if one made the kinds of admixture assumptions that we have been discussing. We have performed this with ForSim, a program that we have developed for such purposes (Lambert et al. 2008; Weiss 2010; Weiss and Lambert 2010; or see popmodels.cancercontrol.cancer.gov/gsr/home). We simulated an initial population of size 1000 that expanded to 10,000 individuals during a run of 10,000 generations with 10 widely separated regions of DNA sequence each 30,000-nucleotides long (the spacing was performed to minimize correlations of sequence patterns among the 10 regions to make their variation statistically independent). Standard human mutation rates within and recombination rates between regions were applied to each generation. We specified that mutations arising in five of the simulated genes would add mutation-specific effects to the value of a simulated quantitative trait. These various values are consistent with estimates for the important basic parameters of the human population since its origin as a distinct species.

The simulated population expanded by diffusion from a local area outward across a square space represented by an X-Y coordinate grid. Each individual has a coordinate location at birth. Mating is random with respect to genotype and phenotype, but males choose females randomly from the surrounding adjacent coordinate locations. Offspring “live” in a location surrounding that of their “father” by a distance randomly chosen from a Normal (0,1) distribution of displacement in both X and Y directions. This is not intended as a rigorous but reasonable algorithm for simulating typical ancestral human mating distances and the diffusion of genetic variants (Cavalli-Sforza and Edwards 1964; Cavalli-Sforza et al. 1994). The values can all be adjusted in performing the simulation should one wish to explore the results. In some runs, we imposed weak directional selection on the trait to see whether that made any difference in the nature of the results.

At the end of the simulation, the simulated space was divided into 10 equal sampling boxes along the diagonal of the occupied space, and all of those boxes that had become inhabited during the run were used as “populations” for input to admixture-based analysis, with K set to the number of such samples. The results are shown in Figure 5 (in different runs, the number of populations ranged from K = 7 to 10). Note that imposing such boxes on what was, in fact, a continuously behaving distribution is just the kind of artifice that is typical of much of human genetics. Note that because the structure-analytic assumption is that one is not necessarily directly sampling any parental (they all are treated as ancestral), one can divide the result in arbitrary ways. Thus, population boundaries we used are not shown in the figure.

Figure 5.

Admixture structure analysis when there is no admixture structure. As described in the text, results are shown from 10 independent ForSim simulations of gradual population expansion under identical conditions. In the admixture structure analysis of each run, K = 7–10 parental populations were assumed as program inputs (but not shown in the figure), although there were in fact no such discrete populations, nor any admixture among them. The data were analyzed using STRUCTURE (Pritchard et al. 2000), and results plotted with DISTRUCT (Rosenberg 2004), commonly used programs for this kind of analysis and portrayal.

If one compares the typical empirical result shown in Figures 2 and 3 to the simulated data in Figure 5, the general picture in the simulated data clearly resembles the real data. The resemblance is even greater for more geographically detailed real-data sets (e.g., Rosenberg et al. 2002; Li et al. 2008; Wang et al. 2008; Tishkoff et al. 2009). There is local similarity and more admixture between nearby regions. Yet, unlike real human history, the ForSim simulation involved no geographic irregularities or migration barriers that might affect the smooth diffusion of allele frequencies. Indeed, the structure analysis of the simulated data included all SNPs rather than using fewer, widely spaced, high-frequency SNPs likely to be polymorphic across the population range.

Figure 5 shows an inferred admixture history that, in the case of simulated data, is 100% fictional and reveals how thoroughly non-Darwinian are the assumptions of such analysis to real-world data. In fact, what we have simulated is essentially gradual isolation by the distance process of human population expansion and habitation, which is roughly how human history actually worked until the recent, rapid large-scale distant-travel centuries. The differences among independent runs under the same parameters shown in Figure 5 also reveal the probabilistic (chance) aspects of what structure analysis will find as the appearance of multiple parental populations and their admixed descendants. Including natural selection in the simulations, geographic bottlenecks, a serial-founder expansion, or off-diagonal sampling boxes make no qualitative difference to the results (data not shown).

For Figure 5 we made no attempt to optimize the analysis because there are too many ways one might manipulate them to obtain desired results. But does the choice of K lead to an artifactual appearance of admixture structure in our simulated data? Figure 6 shows a comparison of one of our runs comparing K = 8 and K = 3 for data from a given simulated run; here, and in the published literature, these K values are arbitrary with regard to the qualitative nature of the resulting figures. Smaller K (fewer parental populations) generally yield an appearance of simpler, more “obvious” pure and admixed individuals. The results are essentially like those shown in Figure 2, which shows that what we are simulating reveals the empirical problems we have tried to raise. To be clear, the point of this type of simulation is not to generate a model of the real global human population, but to show that simulating the same kinds of processes as generated the geographic distribution of human genetic variation can give an entirely false appearance when analyzed under the counterfactual assumptions of structure analysis. In this sense, it is the assumptions of the analysis rather than true historical Darwinian facts that generate the results.

Figure 6.

Assumptions affect results of admixture analysis. Smaller assumed numbers of ancestral populations make admixture from parental populations seem somewhat simpler because there are fewer parentals to draw from, although this is entirely an artifact of the analysis. Here, the same set of simulated data were analyzed as in Figure 5, assuming K = 8 (top) and K = 3 (bottom) parental populations.

One might argue—correctly!—that the nature of these results is entirely obvious; if a program is designed to find ancestral populations and admixed individuals, then, of course, that is what it will find unless there was complete random mating in the entire global population. Nor, of course, does the similarity of simulated to real data by itself prove that admixture-based analysis is not finding historical truth. It works well, for example, when the situation is reasonably well understood historically, as in the case of African- or Mexican-Americans, whose admixture history was major, rapid, recent, and historically documented. But how can one tell? Because there are manifest reasons why there are not, and may never have been, truly isolated “ancestral” human populations in the admixture-structure sense, why use the approach or accept its results as true?

If this kind of analysis were strictly a digest of convenience as a way of portraying the relationship between location and genetic similarity, it could be unexceptionable. But investigators presenting such analysis almost universally imply real, not fictive history as if the parentals really did, or do, exist as such. Categorical treatment of humans has caused great grief in history, especially because if groups are different in terms of genetic variation and one takes a Darwinian assumption that traits are all here because of natural selection, then one easily slips into judgments of the inherent value of genes, and hence the people, in different race categories, whether that word is used to refer to the populations or not.

Instead of such an approach, there are other ways to analyze human variation, using the same data, that produce comparably esthetic graphical portrayal of its pattern over space that are more properly interpretable in terms of the actual evolutionary generating processes. Those processes have clearly been typified by local exchange of mates between nearby small populations as the human frontier gradually expanded out of Africa to populate the rest of the world. Even language, culture, and local geography as a rule only provide leaky barriers to such exchange. With today’s instant access to global observations on a systematic scale, there should be no excuse for taking a typological viewpoint about human variation, be it statistical or otherwise.

WHY?

Why are we humans, scientists, and lay public alike so prone to perpetuate the categorical thinking of the past? What is at the root of such thinking? Is there any reason we should have come to that when we have always known that variation was more graded? Perhaps these are philosophical questions, or perhaps the answer would be a rather generic appeal to the evolutionary survival value of quick recognition of categories: food, mate, friend, or foe.

But this is the age of science in which we should be able to override such primeval reactions. The discovery of evolution as a population process that produces spatial and temporal variation in basically quantitative ways should have easily purged us of erroneous categorical thinking. There are, in fact, alternative ways to choose and analyze samples that do not make the typological assumptions.

These points are about admixture-based portrayals of human history. It may still be valuable to use structure-based analysis as a pragmatic way of accounting for uneven genotype frequency distributions across sampling space in the context of genetic mapping and inference related to identifying genes causally associated with diseases or other traits of interest. Even our pure diffusion-based simulated population process leads to genetic variation across space so that the spectrum of genotypes in one area is not identical to those in other areas; the greater the distance, the greater the difference.

This does not gainsay the value of some aspects of human categorical concepts. Self-defined ethnicity (Tang et al. 2005b) must be valuable as a convenient way to capture something about individuals sampled in epidemiology because it affects not just their marriage patterns, but also their habits and environmental exposures. That “something” is largely cultural, although it also has some correlation with geographic ancestry and, hence, genetic variation. Races, in this sense of social cohesion, that people choose to use about themselves and their community, certainly do exist; people with cultural affinities can have irregular and genome-wide characteristics, but whether or not they are usefully correlated with genetic causation of phenotypes such as disease, epidemiological objectives are different from inferring population history. History is a fact, not a convenience.

Linnaeus was a brilliant scientist who contributed foundational ways of organizing Nature’s species. The Linnaean categorical framework raised the challenge to explain the origin of those categories and, perhaps, provided Darwin with a foil against which to evaluate his observations about variation. But one Linnaeus was enough.