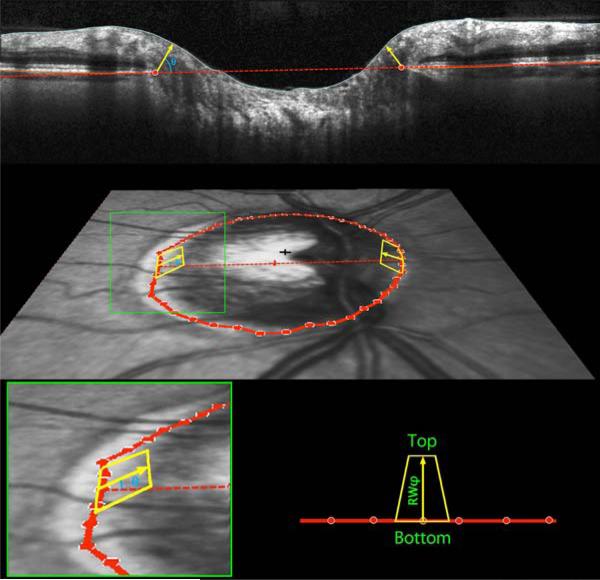
Figure 2. Definition and calculation of Bruch's Membrane Opening Minimum Rim Width and Minimum Rim Area, as used to Estimate the Amount of Neuroretinal Rim Tissue in Glaucoma.
(Top) Within each of the 24 radial scans, Bruch's Membrane Opening was delineated (red circles). The minimum rim width within that sector was defined as the shortest distance from this point to the Inner Limiting Membrane (yellow arrow, at angle θ above the Bruch's Membrane Opening plane). These were averaged across sectors to give the global measure Bruch's Membrane Opening Minimum Rim Width. (Middle Panel) Within each sector, rim areas (yellow trapezoids) were calculated as the areas of trapezia at varying angles above Bruch's Membrane Opening plane. The height of each trapezium equals the rim width at this angle, referred to as RWθ. The base equals the circumference within that sector, 2πr/48, where r represents the distance from Bruch's Membrane Opening centroid (red cross). The top then has length 2πr / 48 × (r – RWθ * cos(θ)). (Bottom Panel) Within each sector the smallest such area was found, at angle φ, and its area calculated as (top+bottom)×RWφ/2. Note that RWφ will not always be the minimum rim width within this sector, as illustrated in Supplementary Figure S1. The global measure BMO-MRA is generated by summing the areas of these 48 trapeziums.