Figure 2.

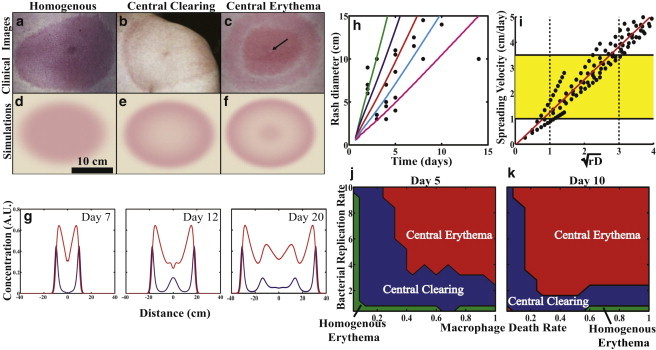
Pathogen-host dynamics recreate the Lyme disease rash. Clinical images of (a) homogeneous erythema, (b) central clearing, and (c) central erythema (arrow points at punctum) taken from Dandache and Nadelman (3) and Nadelman and Wormser (31), and reprinted with permission from Elsevier and Robert Nadelman. (d–f) The model recreates all three rash morphologies using realistic parameter values. (g) Time series of the spatiotemporal evolution of a central erythema, showing normalized bacterial (blue) and macrophage (red) densities at three separate time points. (h) Comparing the model results with different bacterial diffusion coefficients (2 cm²/day (green), 1 cm²/day (blue), 0.5 cm²/day (red), 0.25 cm²/day (cyan), and 0.1 cm²/day (magenta)) to clinical data on the spread of the rash (21) suggests that D ∼ 0.25 cm²/day. (i) The model predicts that spreading rate is proportional to the square-root of the replication rate and diffusion coefficient (yellow box). Clinically observed range of spreading velocities; (dashed lines) predicted range for the product of the bacterial replication and diffusion rates. (j–k) Phase diagrams for the rash morphologies at two time points illustrate that the primary parameters controlling rash morphology are the macrophage clearing rate, spirochete replication rate, and time since infection. (d–f) See Movie S1, Movie S2, Movie S3, Movie S4, Movie S5, and Movie S6 in the Supporting Material. To see this figure in color, go online.