Abstract
Studies examining the relationship between neighborhood social disorder and health often rely on multiple informants. Such studies assume interchangeability of the latent constructs derived from multiple-informant data. Existing methods examining this assumption do not clearly delineate the uncertainty at individual levels from that at neighborhood levels. We propose a multi-level variance component factor model that allows this delineation. Data come from a survey of a representative sample of children born between 1983 and 1985 in the inner city of Detroit and nearby middle-class suburbs. Results indicate that the informant-level models tend to exaggerate the effect of places due to differences between persons. Our evaluations of different methodologies lead to the recommendation of the multi-level variance component factor model whenever multiple-informant reports can be aggregated at a neighborhood level.
Keywords: Interchangeability, multiple-informant data, multi-level models, neighborhood effects
1. Introduction
We examine the assumption that reports from multiple informants are interchangeable when estimating a latent trait aggregated to a cluster level. Use of multiple informants to assess outcome and suspected risk factors is common in many research areas [1]. The disagreement between multiple-informant reports is not a problem when each informant can provide distinct information about the targeted variable. For example, dissimilar reports of child behaviors by parents and teachers may result from differences in how children behave at home and at school [2]. In this case, each informant provides distinct information and a separate analysis for each of the informants' reports may be appropriate. However, in many cases, multiple informants report on a single trait. For instance, multiple respondents within a neighborhood may be asked to report on their neighborhood's safety. In such cases, multiple-informant reports are, in theory, interchangeable, i.e., measuring the same underlying trait, and separate analyses are not ideal. In practice, discordance across reports is common.
Different methods for resolving discordance in this setting have been proposed. When the informant data are used as predictors or outcomes directly, i.e., as manifest variables, a number of ways of integrating reports has been reviewed by Horton et al.[3] among others. When the targeted variable is a latent trait that cannot be directly measured or can only be measured with error, the latent variable and measurement error models are more appropriate [4]. Kraemer et al.[5] proposed an approach that identifies informants based on separating the influence of contexts and perspectives from that of the true construct of the characteristic of interest. Horton et al.[6] developed several models for multiple-informant data based on item response theory (IRT). These methods are appropriate when the latent construct is defined at the same level as the informants.
If the latent trait is defined at a different level of clustering than the reporting units, then the validity of the interchangeability assumption should be examined at the appropriate cluster level. We have not found publications that aimed at testing the interchangeability of reports of a latent construct at a cluster level.
Our paper is motivated by the hypothesis of the neighborhood social disorder (NSD) affecting youth behaviors, in which NSD is the latent construct that cannot be directly measured. It is assessed by two informants, youth and one of their parents, with a 21-item questionnaire. The informants are clustered in a neighborhood and the neighborhood-level social disorder is the variable of interest. In the following sections we describe the motivating question, notational conventions, the traditional and proposed analytic approaches to examine the validity of the interchangeability assumption, and methods for testing the hypothesis of interest incorporating multiple-informant data. An example is used throughout the paper to illustrate and compare the proposed methods rather than to provide conclusive substantive evidence. The final section discusses the pros and cons of different methodologies and presents some recommendations.
2. Motivating Question, Data and Notations
2.1 Theory on Neighborhood Effects
In Great American City, Robert J. Sampson [7] recounts the intellectual history of neighborhood effect research, from the social disorganization theory [8] to its descendents, such as the exposure opportunity hypothesis and collective efficacy theory [9–13]. Constructs of neighborhood characteristics typically fall into two general categories.
The first category is broadly defined as neighborhood socioeconomic status, which is usually characterized using aggregates of individual characteristics, typically from Census data. Different studies have used a wide variety of such indicators including poverty, low educational achievement, racial/ethnic diversity and residential instability. Observer/respondent reports of the built and service environment, thought to reflect social differentiation and stratification in a geographic area, have also been used.
The second category uses questionnaires or vignettes to ascertain aspects of social organization, such as social capital/cohesion/control or social disorder. For example, the 13-item Perceived Neighborhood Disorder (PND) scale [14] assesses the physical and social disorder using questions such as “There are a lot of abandoned buildings in my neighborhood” and “There is too much drug use in my neighborhood.” Crum et al. [9] used an 18-item scale to measure exposure to drug and violence in the neighborhood. Because many of these measures stem from the social disorganization theory, we broadly classify them as NSD.
2.2 Study Sample and Measure of NSD
The data came from a longitudinal study of neuropsychiatric sequelae of low-birthweight. Random samples of low birthweight and normal birthweight children were drawn from the 1983 to 1985 newborn discharge lists of two major hospitals, one serving a disadvantaged inner-city community in Detroit and the other serving a suburban middle-class community, in southeast Michigan. For details on the sampling and data collection, see Breslau et al.[15–17].
We used the questionnaire developed by Crum et al.[9] to measure NSD and added three items related to problems of violence or crime. Data on NSD were gathered from 610 mother-youth pairs when the youths were 17 years of age. The 21-item questionnaire includes 7 out of the 13-item PND scale [14], and 7 out of the 10-item NSD in Hill and Angel [18]. (See Table 1 for the items.)
Table 1. Neighborhood disorder reported by parent and youth.
| Total (n=610) |
Urban (n=238) |
Suburban (n=372) |
|||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Item | Neighborhood Disorder | Parent % True | Youth % True | Parent % True | Youth % True | Parent % True | Youth % True |
| 1 | Within working distance of my house there is a park or playground where people can walk or children can play games (R) | 16.07 | 17.87 | 20.17 | 20.59 | 13.44 | 16.13 |
| 2 | There are plenty of safe places to walk or play outdoors in my neighborhood (R) | 14.10 | 17.05 | 29.83 | 33.61 | 4.03 | 6.45 |
| 3 | Every few weeks, some kids in my neighborhood gets beat-up or mugged | 5.25 | 13.61 | 12.61 | 25.21 | 0.54 | 6.18 |
| 4 | Every few weeks, some adult gets beat-up or mugged in my neighborhood | 5.08 | 8.52 | 11.34 | 17.65 | 1.08 | 2.69 |
| 5 | In my neighborhood, I see signs of racism and prejudice at least once a week | 4.43 | 12.13 | 4.62 | 7.14 | 4.30 | 15.32 |
| 6 | In my neighborhood, many yards and alleys have broken bottles and trash lying around | 10.16 | 29.02 | 22.27 | 57.98 | 2.42 | 10.48 |
| 7 | There is drug use or drug traffic in my neighborhood | 25.74 | 42.79 | 44.96 | 60.50 | 13.44 | 31.45 |
| 8 | Before or after school I often see drunken people on the street in my neighborhood | 11.31 | 18.20 | 25.21 | 42.86 | 2.42 | 2.42 |
| 9 | Most adults in my neighborhood respect the law (R) | 6.39 | 15.25 | 13.45 | 33.61 | 1.88 | 3.49 |
| 10 | There are abandoned or boarded-up building in my neighborhood | 14.92 | 21.15 | 31.09 | 47.48 | 4.57 | 4.30 |
| 11 | I feel safe when I walk around my neighborhood by myself (R) | 10.98 | 14.59 | 23.53 | 30.67 | 2.96 | 4.30 |
| 12 | The people who live in my neighborhood often damage or steal each other's property | 6.07 | 14.10 | 13.03 | 25.63 | 1.61 | 6.72 |
| 13 | The people who live in my neighborhood always take care of each other and protect each other from crime (R) | 19.67 | 35.90 | 28.15 | 50.84 | 14.25 | 26.34 |
| 14 | Almost every day I see homeless people walking or sitting around in my neighborhood | 7.54 | 16.07 | 13.87 | 33.61 | 3.49 | 4.84 |
| 15 | In my neighborhood the people with the most money are the drug dealers | 5.08 | 15.74 | 10.08 | 34.03 | 1.88 | 4.03 |
| 16 | In my neighborhood there are a lot of poor people who don't have enough money for food and basic needs | 6.56 | 13.44 | 13.45 | 29.41 | 2.15 | 3.23 |
| 17 | For many people in my neighborhood going to church on Sunday or religious days is a very important activity (R) | 21.97 | 32.46 | 24.37 | 32.77 | 20.43 | 32.26 |
| 18 | The people who live in my neighborhood are the best people in the world (R) | 44.75 | 71.64 | 56.30 | 81.93 | 37.37 | 65.05 |
| 19 | When coming or going from my neighborhood I have to plan carefully to avoid being a victim of violence or crime | 9.02 | 15.57 | 21.01 | 34.45 | 1.34 | 3.49 |
| 20 | I often hear gunshots in my neighborhood | 12.30 | 17.70 | 28.15 | 40.34 | 2.15 | 3.23 |
| 21 | Gang-related crime or violence is a problem in my neighborhood | 4.59 | 11.64 | 10.50 | 26.05 | 0.81 | 2.42 |
|
| |||||||
| Total Score (range 0 to 21) Mean (Standard deviation) | 2.62 (3.31) | 4.54 (4.38) | 4.58 (4.06) | 7.66 (4.86) | 1.37 (1.86) | 2.55 (2.49) | |
Note: R = Reverse coding. The 21-item true-false measure of neighborhood disadvantage was adapted from Crum et al.[9] by adding three items related to violence or crime problems.
We created total scores, separately for parents and youths, based on the total number of responses indicating disadvantaged neighborhood. The correlation of total scores between the parent reports and youth reports was 0.50 (p<0.001). The mean score of parent-reports was 2.62 with a standard deviation (SD) of 3.31, and the mean score of youth-reports was 4.54 (SD=4.38), i.e., youths perceiving living in a worse neighborhood than their parents.
Figure 1 displays the inter-rater agreement for parent and youth reports using Kappa, Yule's Q and intraclass correlation coefficient for the overall, urban and suburban samples [19], sorted by the overall Kappa. There were only 4 items for which all three statistics indicated higher agreement in urban areas: item 3) “Every few weeks, some kids in my neighborhood gets beat-up or mugged;” item 8) “Before or after school I often see drunken people on the street in my neighborhood;” item 18) “The people who live in my neighborhood are the best people in the world;” and item 19) “When coming or going from my neighborhood I have to plan carefully to avoid being a victim of violence or crime.” These statistical measures are informative, but they do not provide a global test for the interchangeability assumption.
Figure 1.
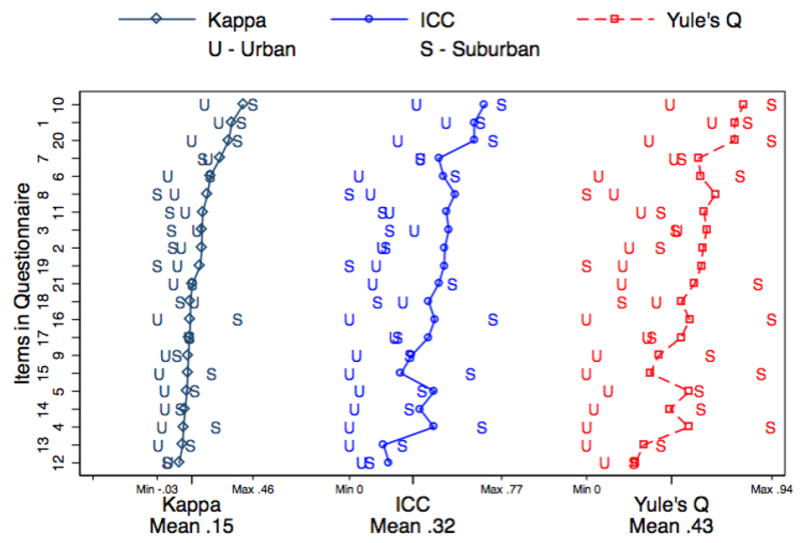
Agreement between parent and youth, overall (connected lines) and in urban (labeled “U”) and suburban (labeled “S”) areas, measured by Kappa, intraclass correlation coefficient, and Yule's Q. Agreement is higher in suburban areas in general (U is to the left of S).
2.3 Notations
In a sample of size N the outcome for the youth in the ith dyad of two informants is denoted byYi, the latent construct, NSD, is denoted by unsd whose subscript is not denoted by i intentionally, and Q covariates measured without error (with a constant in the first column to simplify notations later) are zi = (1, zi1,…, ziQ)′, for i =1,…, N. For purposes of illustration throughout the paper we use a binary indicator “ever smoking a cigarette by age 17” as the outcome of interest. Some methods outlined below can be easily extended to multiple outcomes. The covariates zi used in all analyses below included gender and race of the youth, mother's marital status, and child-reported parental monitoring at age 11. Parental monitoring was measured by the instrument in [20], adapted from [21]. Bohnert et al.[22] found parental monitoring affected smoking behaviors in White children. Minority, urban residents, single and less educated mothers were more likely to live in a disadvantaged neighborhood.
The latent variable is assessed through responses to J items in the questionnaire, denoted by with superscript (s) denoting the specific informant, s=1 for youth and s=2 for parent. Traditional approaches are usually based on the sum of all items, properly coded for neighborhood disadvantage. For all S informants, let where denotes the total score for the s-th informant.
The outcome model relates Yi and unsd through a generalized linear model with a link function g(·),
| (1) |
where μ = E(Yi | zi, unsd), β = (β0, β1,…, βQ)′ is a (Q + 1)×1 vector of unknown parameters and βu is the parameter of interest. The notation βu should not be confused with the component of the vector β. For binary outcomes, μi is the probability of success, Pr(Yi = 1|zi,unsd) and the canonical link function of g(·) is the logit link,
| (2) |
The inverse of the logit link is sometimes called the expit function, f (·), with
| (3) |
Substituting unsd with the informant-specific total score or a consensus between the informant reports, wi without any superscript, into equation (1) leads to a substantively different model,
| (4) |
where, with a slight abuse of notation, μI = E(Yi|zi,wi) and the parameter βw represents the odds ratio of one unit increase in wi (or in if it replaces wi in (4)). This parameter isfundamentally different from βu because the two models have a different philosophical underpinning. Methods and results for estimating βw are available upon request.
3. Analytic Approaches
3.1 Overview
The concept of interchangeability can be operationalized in two ways: first, there is one underlying distribution of the latent variable of interest, and second, there is a unique effect of the latent variable on the outcome. Thus, the empirical distribution of the latent variable based on report from one informant should be the same as the one derived from another informant; and the effect estimated based on one informant report should be the same as the one estimated from another. Horton et al.[6] developed several models for multiple-informant data based on the IRT. We extend their model and demonstrate step-by-step how to (a) estimate the latent trait at a cluster level, and (b) estimate the effect of the latent trait using different approaches. We then compare the empirical Bayes predictions of the latent variable by multiple informants; and test the hypothesis that the impact of the latent variable on the outcome is the same using either informant's report (see section 3.3.2 and 3.3.3).
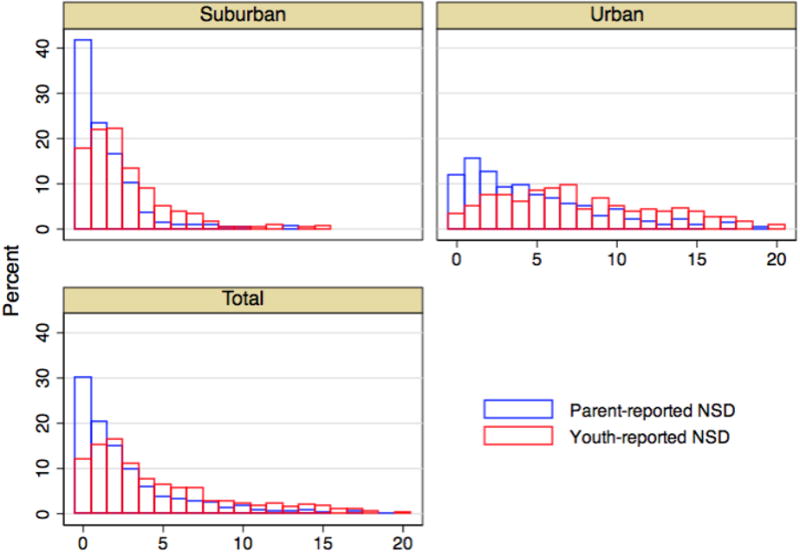
Applying the measurement error model framework to multiple-informant data is reasonable provided that appropriate distributional assumptions are made for the error and the unobserved variable. In Figure 2, we see that the distributions of the total scores in urban and suburban areas had different shapes and neither score can be satisfactorily transformed to a normal distribution. The distribution of the total scores in inner city Detroit (urban) area is rather flat whereas in the middle-class suburban area the scores cluster near the lower end of the scale. Nonparametric models for covariate measurement errors have been developed for binary outcomes [23]. These models implicitly assume the two-informant reports are replicates of sort (perhaps with a drift in means). We first review some analytic approaches that allow the identification of βu under different assumptions.
Figure 2. Distribution of the total scores based on parent- and youth-reported 21 items in the questionnaire of neighborhood social disorder.
3.2 Classical Measurement Error (CME) Model
We use the CME model as the starting point to illustrate how we relax the assumptions in CME to allow non-normal distributions and the use of IRT to build a more theoretically grounded model.
Let's assume equation (1) is a correctly specified model for the outcome, and and are the two fallible measures (surrogates) for the underlying construct unsd and the measurement errors are nondifferential, i.e., . The CME model assumes
| (5) |
The measurement errors are independently normally distributed with zero mean and constant variance σ2. It is known that substituting in equation (1) will lead to a biased estimator of βu; and several approaches have been developed to correct this bias [4].
3.2.1 Regression Calibration (RC)
The RC method [24] is feasible when there are either replicated surrogates (such as multiple-informant data), validation data or instrumental variables. The essential step in RC is to substitute unsd in equation (1) by an estimate of E(unsd | wi, zi)[25]. The resulting estimate of βu is consistent for linear models under the nondifferential measurement error assumption; and it is inconsistent for logistic regression, but usually with small bias ([4], pp. 90-92). The RC estimates of the underlying construct NSD for smoking are shown in Table 2 column 1. The effect was not statistically significant for urban areas (β̂u = 0.1). For suburban areas the odds ratio of NSD for smoking is exp(β̂u) = 1.42(p<0.01). Note this estimate is greater than the estimated exp(β̂w) assuming no measurement errors (results available upon request), consistent with the attenuation effect of covariate measurement errors.
Table 2. Estimates of βu — effects of latent neighborhood social disorder on youth smoking.
| 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|
|
| ||||||
| Urban Areas | RC | SIMEX | IV | Person-level Factor Model |
Census Tract-level Factor Model |
|
| β̂u | 0.100 | 0.063 | 0.039 | |||
| (s.e.) | (0.132) | (0.069) | (0.075) | |||
|
|
0.280 | 2.042 | ||||
| (s.e.) | (0.124) | (1.264) | ||||
|
|
−0.094 | −2.001 | ||||
| (s.e.) | (0.123) | (1.468) | ||||
|
| ||||||
| Suburban | ||||||
| Areas | ||||||
| β̂u | 0.352** | 0.304** | 0.061 | |||
| (s.e.) | (0.140) | (0.107) | (0.093) | |||
|
|
0.883** | 1.182** | ||||
| (s.e.) | (0.212) | (0.597) | ||||
|
|
−0.485** | −0.768 | ||||
| (s.e.) | (0.238) | (0.589) | ||||
Note: RC = Regression calibration; SIMEX = simulation extrapolation; IV = instrumental variables approach. p -value: * < .05 ** <.01. Other variables included in the regressions were youth gender, race, mother's marital status, youth-reported parental monitoring at age 11. The correlations for the underlying factors in the family-level factors model were 0.34 for urban informants and 0.67 for suburban informants. The correlations for the underlying census tract-level factors in the multi-level mode were 0.81 for urban areas and 0.90 for suburban areas.
3.2.2 Simulation Extrapolation (SIMEX)
The SIMEX method [26] generates a scaled measurement error with , typically θ = (0.5,1,1.5, 2), and estimates through a series of simulated samples, together with the naïve estimate under the assumption θ = 0. These estimates will be used in an extrapolation function (typically a quadratic function) to extrapolate to the case with no measurement error, i.e., θ = −1 to get an unbiased estimate of βu[27]. The results using SIMEX are shown in Table 2 column 2. The estimates are slightly smaller with smaller standard errors than the estimates using RC. The conclusions however remain the same.
3.2.3 Instrumental Variables
In the absence of replication and validation data or when the fallible measures are differential, estimation of the parameter of interest βu is still feasible provided that the data contain an instrumental variable (IV), denoted by Ti (using the vector Ti for multiple instruments), that satisfies certain assumptions. Essentially an IV must be correlated to unsd, it must not be correlated with the residual Yi − E(Yi | zi,unsd), and it must be not be correlated with the measurement error εi [28]. The advantage of the IV approach is that when contains differential errors, such as the self-selection problem (also known as the membership or endogeneity bias), the IV estimator is still consistent. For example, youth with behavioral problems may underreport the neighborhood disadvantage when unobserved factors that lead to behavioral problems also distort perception of the youth, resulting in selection bias in conventional estimates.
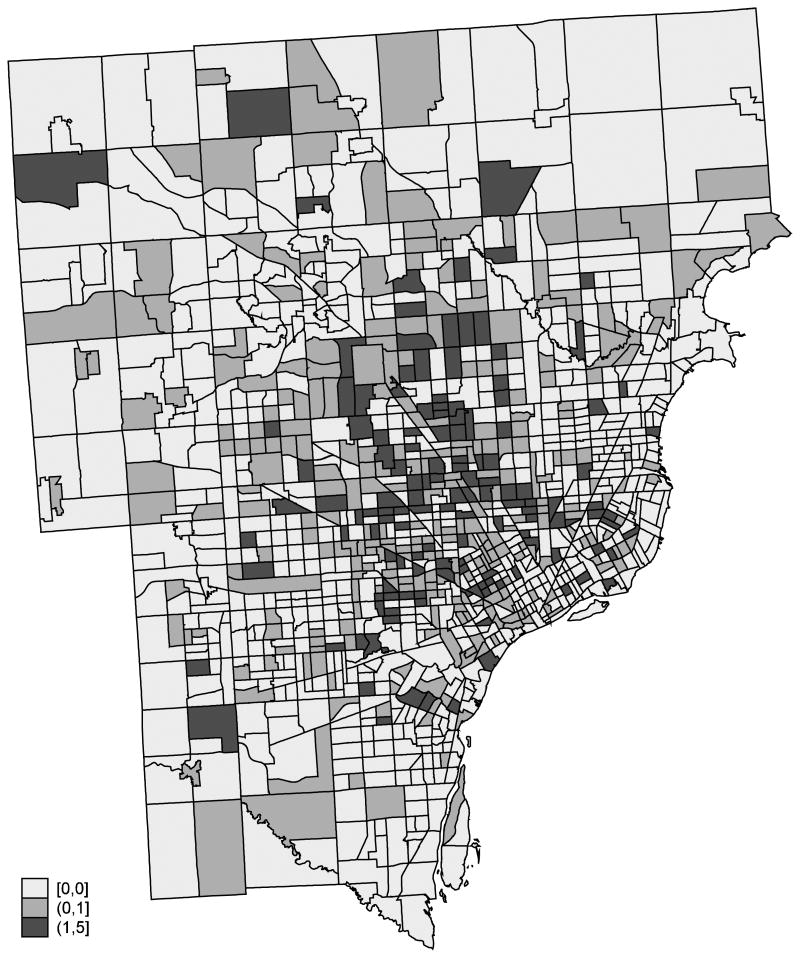
In our data, street addresses of the families were obtained during each interview, and were geocoded using geographic information system (GIS) ArcGIS 10.0 [29]. The geocoded points were spatially joined to the appropriate 1990 or 2000 census tract boundary file [30] that contained neighborhood sociodemographic characteristics. The 610 families interviewed lived in 434 Census tracts (Figure 3) in the tri-county area in southeast Michigan. In 138 Census tracts more than one family per tract participated in the study. In 296 Census tracts only one family participated in each tract. We can see more clustering in some areas of the map. We chose the census variables that were most predictive of youth- and parent-reported NSD (based on the adjusted R-square statistics) as IV's, including percent of female-headed households, percent households with children age 5 to 18 years below federal poverty line, percent population with less than high school education and unemployment rates, and found β̂u = 0.04 in urban areas and β̂ u = 0.06 in suburban areas, neither of which was statistically significant.
Figure 3.
Families in Study Sample: Census tracts labeled [0,0] have no observations, tracts labeled (0, 1] have one family per tract (n=296) and tracts labeled (1,5] have two to five families per tract (n=138).
The CME model can also be estimated using maximum likelihood, quasi-maximum likelihood and conditional score methods. The literature is too vast to be presented in the current paper [4]. Models for continuous covariates measured with errors are far more developed than for discrete cases. When the discrete covariate is dichotomous, the literature for misclassification is in turn bigger than the polytomous or ordered discrete covariates measured with errors. When a score is constructed from a few Likert-scale items, the measurement is unlikely to be normally distributed. As seen in Figure 2, the distributions of youth- and parent-reported scores have distinct shapes in urban and suburban areas. In this situation the CME models might be inappropriate. We will present a latent variable approach based on the IRT to uncover βu without relying on the summed scores.
3.3 Proposed Approach
Latent variable models constitute a suite of models for multivariate analyses. In essence, latent variable models link observed continuous or categorical variables, i.e., manifest variables, to unobserved variables or unmeasured constructs, i.e., latent variables. In our study, to fully exploit the multilevel structure of the study we introduce some additional notations. The items in the neighborhood questionnaire are indexed by j, and individual subjects are indexed by i. In addition, consider the clustering of parent and youth in family k and the nesting of families in Census tract l. Thus the superscript (s) in previous notation is no longer needed to index different informants. Both informants i and i′ are nested in family k. The advantage of this approach is that families with data from only one informant can be incorporated in the analysis. For comparison purposes we continue using parent-youth pair data.
The concept of social disorganization is defined as “the inability of a community to realize the common values of its residents and maintain effective social control….These neighborhood-level dynamics were thought to undermine personal ties, voluntary associations, and local institutions, which in turn were hypothesized … eventually leading to outcomes such as crime, delinquency, homelessness and educational dropout” [7]. Shevky and Bell, using Census tracts as units of analysis, developed three constructs—social rank, urbanization/family status and segregation—to reflect social stratification in industrial society [31]. The point to be made is that the influence of neighborhood lies in characteristics of places rather than persons. Thus in our modeling framework, the latent construct of NSD should be defined, and its influence estimated, at a level higher than the individual-level.
3.3.1 Model Specifications
Denote the Q individual-level covariates by zikl = (1,zikl1,…,ziklQ)′ for person i in family k in Census tract l, where i =1,2, k = 1,…,K, and l = 1,…,L. Denote the 21 items in the neighborhood questionnaire by xikl = (x1ikl,…,xJikl)′ with J = 21 and the sum score . Let Yikl be the outcome of interest, e.g., in our study, youth smoking a cigarette by age 17 in which case i = 1 and the notation simplifies to Ykl. At the neighborhood-level the latent variable is denoted by ηl. The observed Census variables, such as the configuration of education and occupation, single female headed households, and racial/ethnic groups, are denoted by vl.
In our proposed models, the measurement model links the neighborhood latent factor ηl with the questionnaire items xikl by a generalized Rasch model or a multilevel variance component factor model [32–34].
To fix ideas, we first present the standard Rasch model, or the logistic one-parameter item response model (IRM),
| (6) |
In the Rasch model, the parameters αj are called difficulty parameters as they represent the level of difficulty of question j in standard tests, and θ ikl are treated as fixed-effects parameters and interpreted as ability of person i. It is worth noting that in our context, these parameters lose their interpretations as difficulty and ability parameters because there is no a priori “correct” answer to the items in the questionnaire. Here θ ikl may represent each informant's perception of NSD and we can estimate differential reporting biases by allowing αj to vary by types of informant, i.e., estimating αji for i = 1,2.
The underlying factors can also be treated as random effects, typically normally distributed. In Horton et al. [6], this factor is used as a regressor for the outcome model, e.g., their correlated bivariate latent trait model assumes:
| (7) |
where (θ1kl, θ2kl) are jointly normally distributed; and only the youth's latent factor affects the outcome. Horton's model can be modified to allow multiple random effects in (7), for example,
| (8) |
where (βc,βP) represent the effects of NSD based on youth-report and parent-report, respectively.
The one-parameter model (6) assumes that the effects of increasing ability is the same for all items on the logit scale, an assumption that can be relaxed using the two-parameter IRM,
| (9) |
where λj represents the extent to which item j discriminates between individuals of different abilities. Usually we fix λ1= 1 for identification. To incorporate the indirect effect of a person-level variable through neighborhood items, an interaction between item indicators and the person-level variable can be added in the measurement models.
It is plausible there might be an “extreme circumstance” factor representing people's additional inclination to regard the neighborhood to be unsafe when violent crimes are involved. In other words, in model (10) below the parameters γj are constrained to zero for all items except for items related to violent crimes (items 3, 4, 11, 19, 20 and 21). This will lead to a two-parameter two-factor model
| (10) |
where φikl is the second factor.
Because parent and youth are clustered in family k, we can extend the one-parameter and two-parameter models by adding a family-level latent variable, υkl,
| (11) |
| (12) |
where θikl represents the deviation of person i's perspective from the family mean υkl. For identification the factor loading λj is assumed to be the same for individual and family latent variables.
Finally, because we are interested in the neighborhood effects, our proposed approach extends the above models to a multi-level variance component factor model by adding the neighborhood factor ηl,
| (13) |
| (14) |
The interpretation of the latent variable ηl is the latent NSD. It is analogous to individual ability in the Rasch model. The latent variable ηl can be modeled in addition by available Census data, e.g.,
| (15) |
where ξl is the tract-level idiosyncratic error. Census variables, if their effects exist, will affect the outcome only indirectly through ηl via equation (15). In our study the majority of Census tracts (68%) had only one family in them. Thus it is likely that υkl cannot be separately identified from ηl, reducing models (13) and (14) to
| (16) |
| (17) |
Ideally, multiple-informant reports of the neighborhood trait should be interchangeable after factoring out individual deviation θikl, i.e., there is a single latent factor ηl based on the data. To test this assumption, we will extend models (16) and (17) to allow two latent factors, and , representing NSD based on parent's and youth's report, respectively. The empirical Bayes predictions of and can be used to examine the interchangeability assumption.
The response model links Ykl with ηl and person-level covariates by
| (18) |
where μkl = E(Ykl|zkl, ηl) = Pr(Ykl = 1|zkl, ηl), and βu is the parameter of interest. If, after factoring out individual deviation, there exist two neighborhood-level latent factors and with different distributions, then we can test if the two factors influence the individual outcome equally. The test can be carried out formally using the following model,
| (19) |
The null hypothesis states that the effects of two latent variables are the same. This, however, is not strictly speaking a direct test of the interchangeability assumption because the null hypothesis only states two variables have the same impact. If the interchangeability assumption holds in the data, then the two factors and should reduce to one factor.
The measurement-models from (6), (9) to (17) assume that conditional on θikl,υkl, and/or ηl all elements in xikl are independent. Thus the joint distribution of all items can be written as a product of univariate probabilities,
| (20) |
where f is the expit function, which depends on the measurement model of choice in equations (6), (9) to (17). For (14), . Combining the measurement model and the response model, the joint distribution of the neighborhood questionnaire items and the outcome can be written as a product of univariate probabilities,
| (21) |
where xkl =(x1kl,x2kl) for two informants' reports.
3.3.2. Estimation
We use a user written Stata program gllamm to carry out the latent variable analyses with adaptive quadrature method for optimization of objective functions [35]. In our study, the one-parameter IRM in (6) was estimated without difficulty, but the two-parameter models in (9) and (10) led to very large condition numbers, defined as the square root of the ratio of the largest to smallest eigenvalues of the Hessian matrix, indicating that the two-parameter models were empirically unidentified. Note that the two-parameter models in (9) have 21 more parameters than the Rasch model in (6). The reduction in likelihood functions was not big enough to endorse the bigger model especially considering the near singularity of the Hessian. Due to the difficulty in estimating the two-parameter models in (9) and (10), we did not expect models (12), (14) and (17) to perform well and they in fact did not converge.
The item characteristic curves based on the one-parameter model for urban parent, urban youth, suburban parent and suburban youth for select items were constructed (available upon request). The differences in the shape and endorsed items in these curves suggest that parent and youth had different difficulty parameters, which was confirmed by increases in likelihoods when parent- and youth-specific difficulty parameters were added. In urban areas, the log-likelihood was −4940.2 for the model with the same difficulty parameter between parents and youths, and it was −4863.0 for the model with distinct difficulty parameters. Similarly, in the suburban areas, the log-likelihood increased from −3559.8 in the former to −3496.1 in the latter. Thus the rest of the analyses allowed different difficulty parameters.
Selection of variance component factor models in equations (11), (13) and (16) can be based on the likelihood ratio comparison but the test statistic is not asymptotically Chi-square distributed under the null hypothesis because of the parameter lies on the boundary of the parameter space. A solution is to use a 50:50 mixture of a point mass at zero and a Chi-square distribution with degrees of freedom equal to the number of extra parameters between two nested models. Compared to models with only a level-1 factor, models with both individual and informant specific Census tract latent factors, and in equation (16), led to further improvement in likelihood (for urban areas, the log-likelihood increased to −4855.2; for suburban areas, the log-likelihood increased to −3455.5).
The coefficients for the individual latent factors θ1kl and θ2kl in the response model (8), are reported in column 4 of Table 2; and the coefficients for the Census tract-level latent factors and , based on model (19), are reported in column 5 of Table 2 (for Stata and SAS codes, see Appendix A and B). Comparing the estimates, we found that using the person-level random effects led to much smaller estimates in suburban areas, potentially leading to a type I error in the effect of NSD. Using the Census tract-level random effects, only the youth-reported NSD is significantly associated with the outcome of ever smoking a cigarette by age 17 . For the suburban areas, using the Census tract-level factor model the test of leads to a Chi-squared statistic of 2.77 (df=1, p-value=0.096); whereas using the person-level factor model the Chi-squared statistic is 10.01 (df=1, p-value=0.002). These results suggest any difference between the two informants' reports lies in personal perceptions but not in their environments.
3.3.3 Model Prediction
We point out two types of prediction of the proposed model (19) — predictions of response probabilities and prediction of random effects; and we focus on the latter. Even though there are different approaches to predicting random effects, the empirical Bayes prediction is the most widely used method for assigning values to random effects [36].
In the context of evaluating the impact of NSD, the random effect of interest is ηl in (18), rather than the informant-level latent variables θikl. In a non-fully Bayesian approach, inference regarding ηl for Census tract l is based on the posterior distribution of η1 given the data and with the model parameters treated as known and equal to the estimates The empirical Bayes prediction of ηl is thus:
| (22) |
It is usually referred to as “expected a posteriori” estimation in IRM and as the “regression method” for factor scoring in factor analysis. Comparative standard errors of the empirical Bayes prediction can be used for making comparisons between clusters if the empirical Bayes predictions have approximately normal sampling distributions. Diagnostic standard errors are the marginal sampling covariance of the empirical Bayes predictions under repeated sampling. They can be used to detect clusters that appear inconsistent with the model.
We selected 12 Census tracts in suburban areas with large, small and intermediate values of the empirical Bayes predictions based on multilevel variance component factor model (19). Table 3 gives the Census tract identifier, cluster size (number of household in each tract), empirical Bayes predictions based on parent-report ηl,p and youth-report ηl,c and the corresponding comparative and diagnostic standard errors. The posterior SD (comparative standard error) is lower than the estimated prior SD (1.07 for ηl,p and 1.08 for ηl,c) and it is smaller for larger cluster size, indicating increasing accuracy of the prediction.
Table 3. Empirical Bayes predictions of neighborhood social disorder, comparative and diagnostic standard errors for 12 Census tracts in suburban areas based on the multilevel factor model.
| Census tract | Cluster size |
|
Standard error |
|
Standard error | ||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
||||||||
| Comparative | Diagnostic | Comparative | Diagnostic | ||||||
| 1251832 | 1 | −1.072 | 0.841 | 0.668 | −0.977 | 0.818 | 0.701 | ||
| 1635546 | 1 | 0.003 | 0.747 | 0.772 | 0.274 | 0.710 | 0.810 | ||
| 1635531 | 1 | 1.956 | 0.658 | 0.849 | 2.349 | 0.636 | 0.869 | ||
| 1251880 | 2 | −0.634 | 0.665 | 0.844 | −0.282 | 0.612 | 0.886 | ||
| 1251815 | 2 | 1.301 | 0.544 | 0.927 | 1.374 | 0.524 | 0.940 | ||
| 1251580 | 3 | −0.798 | 0.601 | 0.891 | −0.617 | 0.547 | 0.927 | ||
| 1251831 | 3 | 0.034 | 0.540 | 0.929 | 0.305 | 0.489 | 0.959 | ||
| 1251816 | 3 | 1.083 | 0.487 | 0.958 | 0.864 | 0.466 | 0.970 | ||
| 1251623 | 4 | −0.830 | 0.588 | 0.899 | −0.640 | 0.514 | 0.946 | ||
| 1251803 | 4 | 0.684 | 0.460 | 0.971 | 0.976 | 0.411 | 0.995 | ||
| 1251965 | 5 | 0.347 | 0.443 | 0.979 | 0.237 | 0.404 | 0.998 | ||
| 1251751 | 5 | 1.001 | 0.412 | 0.992 | 1.309 | 0.373 | 1.010 | ||
Note: Comparative standard errors of the empirical Bayes prediction can be used for making comparisons between clusters if the empirical Bayes predictions have approximately normal sampling distributions. Diagnostic standard errors can be used to detect clusters that appear inconsistent with the model.
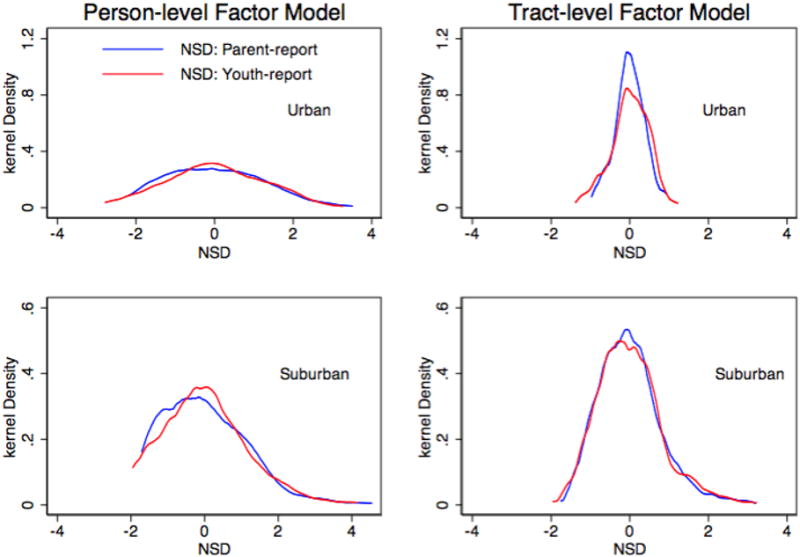
Figure 4 displays the empirical Bayes predictions of person-level θikl (two panels on the left) in model (8) and Census tract-level ηl (two panels on the right) in model (19). The distributions of the underlying factors at the Census-tract level based on parent-reports and youth-reports (curves on the right) are more similar to each other as compared to the distributions of the underlying factors at the person-level (curves on the left).
Figure 4. Empirical Bayes predictions of neighborhood social disorder based on parent- and youth-reported questionnaires.
4. Discussion
Ecological studies aim at evaluating the effect of aggregated economic indicators of communities or NSD on individual outcomes such as crime, delinquency and health. Various survey instruments have been created to ascertain NSD based on individuals' reports.
Discordance among respondents living within the same neighborhood raises a question about the interchangeability, and hence the validity, of individual NSD assessments. In particular, when the interchangeability assumption is made at the cluster level – consistent with the theoretical requirement for examining the impact of NSD – it is important to use multiple-informant data to estimate the latent construct of NSD at the cluster level. We present models that distinguish cluster level latent variables from informant level latent variables.
To model the impact of the latent construct of NSD with multiple-informant reports, one can use the classical measurement error approaches (e.g., regression calibration, simulation extrapolation and instrumental variables) or the Rasch model based on the IRT. However, these models assume the latent variables at the level of the informants. We propose using a multi-level variance component factor (MVCF) model consistent with the prediction of NSD theories because the model differentiates heterogeneity of the persons from the heterogeneity of the places. As previously stated, the model does not rely on the IRT, because it can simply be viewed as hierarchical latent variables model.
In this model we can examine the interchangeability assumption in two ways. First, we can compare the empirical Bayes predictions of the latent variable at the cluster level based on different informants' reports. Second, we can test the hypothesis that the effects of the latent variables on the outcome are the same when multiple reports are used. The advantage of the first approach is that it is a direct translation of the interchangeability assumption into a distributional statement of the underlying latent variable, but the disadvantage is that it is not a formal statistical test. The disadvantage of the second approach is that it is at best an indirect test of the interchangeability assumption based on the hypothesized impact of the latent variable on the outcome under study. When the effects of the latent variable are the same the multiple informant data can be combined to estimate the effect of one latent trait.
In our application, in the first approach, the distributions of the empirical Bayes predictions of the latent variable at the informant level, compared with the empirical Bayes predictions of the latent variable at the cluster level, are less similar between parent- and youth-reports in the suburban area. In the second approach, results of informant-level Rasch model showed significant differences between effects of the latent NSD at the informant level between parent reports and youth reports; however, the results of the MVCF model found no significant difference in the effect of the latent NSD at the cluster level. Although combining the two latent variables into a single one was not a viable option in this application, the approach may be an important strategy to pursue in similar settings.
Compared with the one-parameter IRM, the more flexible two-parameter model at the informant level added 20 more parameters but did not achieve much gain in log likelihood. When we combine the informant and cluster-level (family and/or tract) factors together, the two-parameter models cannot be estimated empirically possibly because the difference between parent and youth within a family is not big enough to identify the factors separately and the number of families within a Census tract is typically small. In a different application with more distinctions between informants and more number of informant per cluster it is possible that the more flexible models can be estimated..
There is a limitation of the MVCF model for this application. The prior distributions of the latent variable in the informant level Rasch model and the MVCF model are both normal. However, the shapes of the empirical Bayes predictions in Figure 4 suggest that there is dispersion of the latent variable in the former for suburban clusters. The normal assumption does not allow dispersion as large as the observed outcomes exhibited in Figure 2. It is unknown how much the underlying construct is dispersed. The normal assumption of the latent variable can be relaxed [23]. Since we are not employing a fully Bayesian approach, evaluating the impact of different prior distributions is beyond the scope of the manuscript.
Our evaluations of different methodologies lead to the recommendation of the MVCF model whenever multiple-informant reports can be aggregated at a cluster level. The results suggest that the informant-level models tend to exaggerate the effect of the places due to differences of the persons. “The fault, dear Brutus, lies not in our stars, but in ourselves”-Shakespeare, Julius Caesar.
Acknowledgments
Funding: This work was supported by National Institute of Mental Health grant R01MH44586 (Breslau) and RC4MH092737 (Luo). We thank Dr. Sue Grady at Michigan State University for geocoding the data. We thank the two anonymous referees for their incisive comments and suggestions for improvement.
Appendix A. Stata Codes for Model (19)
| //Prepare the data in vertical format where outcome and informant-reported //response to the 21 items are stacked together, named “nb” |
| //Create indicators for response types label def type3 0 “Outcome” 1 “parent response” 2 “youth response” label val type type3 |
| gen byte d1 = type==0 |
| gen byte d2 = type>0 |
| //Create dummy variables for the 21 items for patient and child foreach n of num 1/21 { |
| gen byte i`n' = [i==`n' & type==1] |
| } |
| foreach n of num 1/21 { |
| gen byte ic`n' = [i==`n' & type==2] |
| } |
| //Since model adjust for child sex, race, mother's marital status and parental monitoring, these variables are crossed with outcome indicator. foreach x of var male black m_status dm_monitor { |
| gen d1_`x' = d1*`x' |
| } |
| gen byte cons = 1 |
| gen byte parent = [type==1] |
| gen byte youth = [type==2] |
| gen _reg = type+1 |
| //Person ID: pid; Census Tract ID: cid |
| *** final model for suburban areas |
| eq d2 : d2 |
| eq prt : parent d1 |
| eq yth : youth d1 |
| eq f1: fh_pct asstab_pct chd_bp_pct median_hou lshscl_pct |
| keep if detr17==0 |
| eststo: gllamm nb d1 d1_male d1_black d1_m_status i1-i21 ic1-ic21, nocons |
| i(pid cid) nrf(1 2) link(logit logit logit) fam(bin bin bin) fv(_reg) |
| lv(_reg) eqs(d2 prt yth) adapt nip(10) |
| est save suburban_eversmk_adpt_corr, replace |
Appendix B. SAS Codes for Model (8)
| /* Data are prepared similarly as above */ |
| PROC NLMIXED DATA=sub outq=n.suburbqpoint QPOINTS=7; |
| PARMS alpha0=−1.9 alpha1=1.3 alpha2=−0.6 alpha3=0.2 alpha4=−1.7 alpha5=0.9 |
| alpha6=−0.05 |
| betam1=2.4 betam2=4.1 betam3=6.3 betam4=5.6 betam5=3.9 betam6=4.6 |
| betam7=2.5 betam8=4.7 betam9=4.9 betam10=3.9 betam11=4.4 betam12=5.1 |
| betam13=2.4 betam14=4.2 betam15=4.9 betam16=4.8 betam17=1.8 betam18=0.7 |
| betam19=5.3 betam20=4.8 betam21=5.8 |
| betak1=1.8 betak2=2.1 betak3=2.2 betak4=3.3 betak5=2.2 betak6=2.8 |
| betak7=1 betak8=4.4 betak9=4.1 betak10=3.8 betak11=3.9 betak12=3.3 |
| betak13=1.3 betak14=3.7 betak15=3.9 betak16=4.2 betak17=0.9 betak18=-0.8 |
| betak19=4.1 betak20=4.2 betak21=4.5 |
| rho=0.65 sigmak=1.8 sigmam=2.1; |
| if type=0 then plogit = alpha0 + alpha1*thetak + alpha2*thetam + alpha3*male + alpha4*black + alpha5*m_status + alpha6*dm_monitor ; |
| if type=1 then plogit = thetam − p1*betam1 − p2*betam2 - p3*betam3 − p4*betam4 − p5*betam5 −p6*betam6 −p7*betam7 −p8*betam8 −p9*betam9 − p10*betam10 − p11*betam11 −p12*betam12 −p13*betam13 −p14*betam14 −p15*betam15 −p16*betam16 −p17*betam17 − p18*betam18 −p19*betam19 −p20*betam20 − p21*betam21 ; |
| if type=2 then plogit = thetak − q1*betak1 − q2*betak2 − q3*betak3 −q4*betak4 − q5*betak5 −q6*betak6 −q7*betak7 −q8*betak8 −q9*betak9 −q10*betak10 − q11*betak11 −q12*betak12 −q13*betak13 −q14*betak14 −q15*betak15 −q16*betak16 −q17*betak17 − q18*betak18 −q19*betak19 −q20*betak20 −q21*betak21 ; |
| prob = 1/(1+exp(−plogit)); |
| sigmakm=rho*sqrt(sigmak*sigmam); |
| random thetak thetam ∼ normal([0,0],[sigmak,sigmakm,sigmam]) subject=idnum; |
| model resp ∼ bern(prob); |
| predict prob out=suburbpred_p; |
| RUN; |
References
- 1.Wagner SM, Rau C, Lindemann E. Multiple informant methodology: A Critical Review and Recommendations. Sociological Methods & Research. 2010;38(4):582–618. [Google Scholar]
- 2.Achenbach TM, McConaughy SH, Howell CT. Child/adolescent behavioral and emotional problems: implications of cross-informant correlations for situational specificity. Psychological Bulletin. 1987;101(2):213–232. [PubMed] [Google Scholar]
- 3.Horton NJ, Laird NM, Zahner GEP. Use of multiple informant data as a predictor in psychiatric epidemiology. International Journal of Methods in Paychiatric Research. 1999;8(1):6–18. doi: 10.1002/mpr.52. [DOI] [Google Scholar]
- 4.Carroll RJ, Ruppert David, Stefanski LeonardA, Crainiceanu CiprianM. Measurement Error in Nonlinear Models: A Modern Perspective. CRC Press; 2006. [Google Scholar]
- 5.Kraemer HC, Measelle JR, Ablow JC, Essex MJ, Boyce WT, Kupfer DJ. A new approach to integrating data from multiple informants in psychiatric assessment and research: mixing and matching contexts and perspectives. American Journal of Psychiatry. 2003;160(9):1566–1577. doi: 10.1176/appi.ajp.160.9.1566. [DOI] [PubMed] [Google Scholar]
- 6.Horton NJ, Roberts K, Ryan L, Suglia SF, Wright RJ. A maximum likelihood latent variable regression model for multiple informants. Statistics in Medicine. 2008;27(24):4992–5004. doi: 10.1002/sim.3324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sampson RJ. Great American City: Chicago and the Enduring Neighborhood Effect. University Of Chicago Press; 2012. [Google Scholar]
- 8.Shaw CR, McKay HD. Juvenile Delinquency and Urban Areas. Chicago: University of Chicago Press; 1942. [Google Scholar]
- 9.Crum RM, Lillie-Blanton M, Anthony JC. Neighborhood environment and opportunity to use cocaine and other drugs in late childhood and early adolescence. Drug and Alcohol Dependence. 1996;43(3):155–161. doi: 10.1016/s0376-8716(96)01298-7. [DOI] [PubMed] [Google Scholar]
- 10.Jencks C. Center for Urban Affairs and Policy Research. Northwestern University; 1988. The Social consequences of growing up in a poor neighborhood: A review. [Google Scholar]
- 11.Leventhal T, Brooks-Gunn J. The neighborhoods they live in: the effects of neighborhood residence on child and adolescent outcomes. Psychological Bulletin. 2000;126(2):309–337. doi: 10.1037/0033-2909.126.2.309. [DOI] [PubMed] [Google Scholar]
- 12.Robert SA. Socioeconomic position and health: The independent contribution of community socioeconomic Context. Annual Review of Sociology. 1999;25:489–516. [Google Scholar]
- 13.Sampson RJ, Raudenbush SW, Earls F. Neighborhoods and violent crime: a multilevel study of collective efficacy. Science. 1997;277(5328):918–924. doi: 10.1126/science.277.5328.918. [DOI] [PubMed] [Google Scholar]
- 14.Ross CE, Mirowsky J. Disorder and decay. Urban Affairs Review. 1999;34(3):412–432. doi: 10.1177/107808749903400304. [DOI] [Google Scholar]
- 15.Breslau N, Brown GG, DelDotto JE, Kumar S, Ezhuthachan S, Andreski P, Hufnagle KG. Psychiatric sequelae of low birth weight at 6 years of age. Journal of Abnormal Child Psychology. 1996;24(3):385–400. doi: 10.1007/BF01441637. [DOI] [PubMed] [Google Scholar]
- 16.Breslau N, Johnson EO, Lucia VC. Academic achievement of low birthweight children at age 11: the role of cognitive abilities at school entry. Journal of Abnormal Child Psychology. 2001;29(4):273–279. doi: 10.1023/a:1010396027299. [DOI] [PubMed] [Google Scholar]
- 17.Breslau N, Paneth NS, Lucia VC. The lingering academic deficits of low birth weight children. Pediatrics. 2004;114(4):1035–1040. doi: 10.1542/peds.2004-0069. [DOI] [PubMed] [Google Scholar]
- 18.Hill TD, Angel RJ. Neighborhood disorder, psychological distress, and heavy drinking. Social Science & Medicine. 2005;61(5):965–975. doi: 10.1016/j.socscimed.2004.12.027. [DOI] [PubMed] [Google Scholar]
- 19.Agresti A. Categorical Data Analysis. Second. Hoboken, New Jersey: John Wiley & Sons, Inc.; 2003. [Google Scholar]
- 20.Chilcoat HD, Anthony JC. Impact of parent monitoring on initiation of drug use through late childhood. Journal of the American Academy of Child & Adolescent Psychiatry. 1996;35(1):91–100. doi: 10.1097/00004583-199601000-00017. [DOI] [PubMed] [Google Scholar]
- 21.Patterson GR, Capaldi DM. Psychometric Properties of Fourteen Latent Constructs from the Oregon Youth Study. New York: Springer-Verlag; 1989. [Google Scholar]
- 22.Bohnert KM, Ríos-Bedoya CF, Breslau N. Parental monitoring at age 11 and smoking initiation up to age 17 among Blacks and Whites: A prospective investigation. Nicotine & Tobacco Research. 2009;11(12):1474–1478. doi: 10.1093/ntr/ntp160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rabe-Hesketh S, Pickles A, Skrondal A. Correcting for covariate measurement error in logistic regression using nonparametric maximum likelihood estimation. Statistical Modelling. 2003;3(3):215–232. doi: 10.1191/1471082X03st056oa. [DOI] [Google Scholar]
- 24.Carroll RJ, Stefanski LA. Approximate quasi-likelihood estimation in models with surrogate predictors. Journal of the American Statistical Association. 1990;85(411):652–663. doi: 10.2307/2290000. [DOI] [Google Scholar]
- 25.Hardin JW, Schmeidiche H, Carroll RJ. The regression-calibration method for fitting generalized linear models with additive measurement error. Stata Journal. 2003;3(4):361–372. [Google Scholar]
- 26.Cook JR, Stefanski LA. Simulation extrapolation method for parametric measurement error models. Journal of the American Statistical Association. 1994;89:1314–1328. [Google Scholar]
- 27.Hardin JW, Schmeidiche H, Carroll RJ. The simulation extrapolation method for fitting generalized linear models with additive measurement error. Stata Journal. 2003;3(4):373–385. [Google Scholar]
- 28.Hardin JW, Schmeidiche H, Carroll RJ. Instrumental variables, bootstrapping, and generalized linear models. Stata Journal. 2003;3(4):351–360. [Google Scholar]
- 29.Environmental System Research Institute. [Accessed september 12, 2012];2012 http://www.esri.com/what-is-gis/overview.
- 30.U. S. Bureau of the Census. [Accessed september 12, 2012];2012 http://www.census.gov/
- 31.Shevky E, Bell W. Social area analysis: theory, illustrative application, and computational procedures. Stanford University Press; 1955. [Google Scholar]
- 32.Rabe-Hesketh S, Skrondal A, Pickles A. Generalized multilevel structural equation modeling. Psychometrika. 2004;69(2):167–190. [Google Scholar]
- 33.Jeon M, Rijmen F, Rabe-Hesketh S. Modeling differential item functioning using a generalization of the multiple-group bifactor Model. Journal of Educational and Behavioral Statistics. 2013;38(1):32–60. doi: 10.3102/1076998611432173. [DOI] [Google Scholar]
- 34.Jeon M, Rabe-Hesketh S. Profile-likelihood approach for estimating generalized linear mixed models with factor structures. Journal of Educational and Behavioral Statistics. 2012;37(4):518–542. doi: 10.3102/1076998611417628. [DOI] [Google Scholar]
- 35.Rabe-Hesketh S, Skrondal A, Pickles A. Maximum likelihood estimation of limited and discrete dependent variable models with nested random effects. Journal of Econometrics. 2005;128(2):301–323. doi: 10.1016/j.jeconom.2004.08.017. [DOI] [Google Scholar]
- 36.Skrondal A, Rabe-Hesketh S. Prediction in multilevel generalized linear models. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2009;172(3):659–687. doi: 10.1111/j.1467-985X.2009.00587.x. [DOI] [Google Scholar]