Table 1.

Summary of predictions of the theoretical analysis

	Tree,	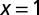Animal,	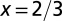Intermediate geometry
Metabolic rate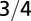
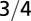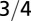Characteristic length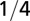
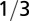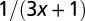Characteristic time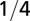
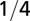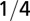Characteristic rate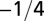
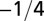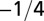Organism volume		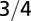1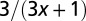
Transport velocity	0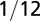
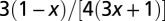Need for pump	No	Yes	Yes
Density		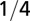0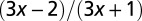
Surface area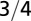
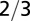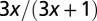Recirculation network	No	Yes	Yes
Fractality of organism	Yes	No	Yes
Service volume density	0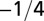
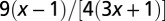Trunk radius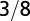

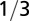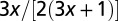The geometry of the organism enters through the scaling of its surface area S with volume V, 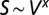. The exponents characterize the scaling of the quantity in the first column with organism mass M. The idealized scaling of the basal metabolic rate, the characteristic time (as reflected in circulation times and life times), and the characteristic rate (such as mutation rates or pump rates) do not depend on the geometry and are universal. Many of the predictions for trees and animals have been observed empirically (10–12, 14–16, 19, 20). The results for organisms with intermediate geometry interpolate between the results for animals and trees.