Figure 2. Filtering exponentials convolved with a system response function.
(a) Exponential on the interval [−1, 1] with Poisson noise added. Amplitude,  , time constant
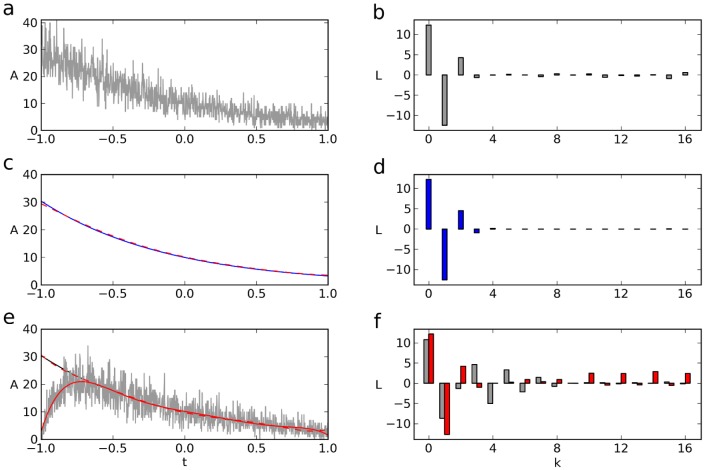
, time constant 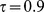 . (b) Legendre spectrum of x as resulting from eq. 5. (c) Mean
. (b) Legendre spectrum of x as resulting from eq. 5. (c) Mean 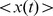 of
of 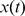 (continuous) and inverse fLT (dashed, eq. 6) of
(continuous) and inverse fLT (dashed, eq. 6) of 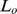 through
through 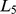 of the spectrum shown in b. (d) Legendre spectrum of the mean
of the spectrum shown in b. (d) Legendre spectrum of the mean 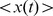 , largely lacking higher noise components. (e) Noisy curve is the convolution of
, largely lacking higher noise components. (e) Noisy curve is the convolution of 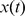 with
with 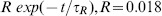 and
and 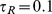 .
. 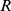 was chosen such that the curve overlaps with
was chosen such that the curve overlaps with 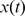 for large
for large  . (f) Legendre spectrum (gray bars) of convoluted noisy exponential shown in e (continuous curve). The lowpass-filtered inverse transform is shown in e (continuous curve) and approximates the convoluted noisy exponential. In addition, f shows the Legendre spectrum of
. (f) Legendre spectrum (gray bars) of convoluted noisy exponential shown in e (continuous curve). The lowpass-filtered inverse transform is shown in e (continuous curve) and approximates the convoluted noisy exponential. In addition, f shows the Legendre spectrum of 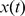 , obtained through eq. 9. The lowpass-filtered inverse transform of this spectrum is shown as the red dashed curve in e and approximates the original non-convoluted exponential, from which the noisy convoluted curve was generated.
, obtained through eq. 9. The lowpass-filtered inverse transform of this spectrum is shown as the red dashed curve in e and approximates the original non-convoluted exponential, from which the noisy convoluted curve was generated.