Estimating population divergence time and phylogeny from single-nucleotide polymorphisms data with outgroup ascertainment bias

Abstract

The inference of population divergence times and branching patterns is of fundamental importance in many population genetic analyses. Many methods have been developed for estimating population divergence times, and recently, there has been particular attention towards genome-wide single-nucleotide polymorphisms (SNP) data. However, most SNP data have been affected by an ascertainment bias caused by the SNP selection and discovery protocols. Here, we present a modification of an existing maximum likelihood method that will allow approximately unbiased inferences when ascertainment is based on a set of outgroup populations. We also present a method for estimating trees from the asymmetric dissimilarity measures arising from pairwise divergence time estimation in population genetics. We evaluate the methods by simulations and by applying them to a large SNP data set of seven East Asian populations.

Introduction

With the fast advance in high throughput genotyping techniques, large single-nucleotide polymorphisms (SNP) data sets have become available for humans (Conrad et al. 2006; Jakobsson et al. 2008) and other organisms such as Drosophila (Chen et al. 2008), cattle (Decker et al. 2009; Gibbs et al. 2009), horse (Brooks et al. 2010), dog (Vonholdt et al. 2010) and pig (Uimari & Tapio 2011). These data are rich in information about past demographic history and are, therefore, widely used in evolutionary studies (Padhukasahasram et al. 2006; Lohmueller et al. 2009; Yin et al. 2009; Pavlidis et al. 2010), for example in the estimation of the history of population divergence, also called the population phylogeny or population tree. Many populations, including most human populations, cannot be described by only considering population divergence without gene flow (Schaffner et al. 2005; Hey 2010; Wang & Hey 2010). Population trees estimated assuming absence of gene flow among populations may be biased in one way or another when gene flow is truly present. However, even in these cases, the estimation of population trees is a useful abstraction for illustrating the relationship between populations and is the main topic of this study.

Genealogy-based methods have been developed for estimating population phylogenies from sequence data (Rannala & Yang 2003; Hey & Nielsen 2007; Heled & Drummond 2010). These methods calculate the likelihood/posterior probability of observed data by considering the underlying coalescent trees/genealogies that describe the ancestry of the sampled sequences. In the next step, a Markov Chain Monte Carlo (MCMC) approach is implemented to integrate over all possible coalescent trees to obtain estimates of demographic parameters and population phylogeny. A related method by Liu & Pearl (2007) implemented in the program BEST uses a sample of coalescent trees obtained using generic phylogenetic MCMC methods as input and then estimates demographic parameters using a type of importance sampling weighting of the sampled trees. Finally, a method described by Kubatko et al. (2009) implemented in the program STEM treats the sampled genealogies as if they were data and then proceeds to estimate the population history using maximum likelihood.

In general, the genealogy-based methods assume no recombination within each locus and free recombination between adjacent loci. However, in most organisms (vertebrates, insects and most plants), recombination rates and mutation rates are of similar magnitude. As a result, nearby SNPs are in linkage disequilibrium with each other but have typically experienced a few recombination events in their genealogical history. Therefore, for most organisms, it might not be appropriate to assume no recombination within loci containing more than one SNP. The evolutionary history at such loci is better described by an ancestral recombination graph (ARG), instead of a simple coalescent tree. Unfortunately, full analysis of the ARG is usually not tractable for most problems and certainly not for large SNP data sets. Therefore, many studies on large SNP data sets use composite likelihood methods that treat sites as if there were independent (Garrigan 2009; Gutenkunst et al. 2009; Naduvilezhath et al. 2011). Such composite likelihood estimators often have desirable statistical properties such as consistency (Wiuf 2006).

Analyses of genome-wide SNP data are associated with additional challenges. Helyar et al. (2011) recently reviewed several common issues in analysing SNP data, one of which being the effects of ascertainment bias. Many studies have pointed out that SNP data are often subject to an ascertainment bias (Kuhner et al. 2000; Wakeley et al. 2001; Akey et al. 2003; Nielsen & Signorovitch 2003; Nielsen et al. 2004). This bias arises from the SNP discovery process. Single-nucleotide polymorphisms used in genotyping are generally discovered by resequencing samples in a small discovery panel. Single-nucleotide polymorphisms with high minor allele frequency (MAF) are more likely to appear polymorphic in the panel and be discovered, than those with low MAF. This introduces a bias towards common alleles. In addition, the samples used for discovering SNPs may not be representative for the samples that are later genotyped, leading to a further bias of the Site Frequency Spectrum (SFS) (Nielsen 2004; Albrechtsen et al. 2010). This bias in the distribution of allele frequencies will also translate into errors and biases when estimating population history and other demographic parameters (Schlotterer & Harr 2002; Marth et al. 2004; Morin et al. 2004; Novembre & Rosenblum 2007; Storz & Kelly 2008; Guillot & Foll 2009; Chen et al. 2010; Moragues et al. 2010). The magnitude and direction of the bias depend on the SNP discover strategy, number of chromosomes included in the discovery panel and the demographic history of the populations (Akey et al. 2003; Helyar et al. 2011).

Several maximum likelihood methods have been developed for estimating population branching patterns and divergence times from the joint SFS for multiple populations using composite likelihood methods (Nielsen et al. 1998; RoyChoudhury et al. 2008; Bryant et al. 2010). In the original implementation by Nielsen et al. (1998), it is assumed that no mutation occurs after population divergence and that genetic drift can be modelled by a neutral coalescent model (Kingman 1982). The likelihood function is calculated by first conditioning on the allelic configuration of the ancestral lineages at the internodes of the population tree and then summing over all possible ancestral configurations. The (composite) maximum likelihood estimate is then found by maximizing over all population divergence times and topologies of the population tree. One obvious drawback of this method is that the computational time increases dramatically as the number of populations increases. To speed up the likelihood calculation, RoyChoudhury et al. (2008) devised a two-stage pruning algorithm that enables efficient summation and optimization. Bryant et al. (2010) developed a similar method, which also takes into account the effect of mutation. Recently, Gutenkunst et al. (2009) implemented a diffusion approximation method for demographic history inference. Their method accommodates a parameter-rich model that incorporates mutation, population size change, selection, migration and admixture.

An important assumption for these methods is that the ancestral population has reached mutation-drift equilibrium. The ancestral SFS can then be calculated using appropriate mutation models (Wright 1931; Kimura & Crow 1964; Kimura 1969). However, in most cases the assumption of mutation-drift equilibrium in the ancestral population is probably not realistic. Moreover, as SNP data are often subjected to an ascertainment bias, the frequency spectrum in the ancestral population may deviate from the expectation. Some methods have implemented an ascertainment correction procedure to account for the ascertainment bias (RoyChoudhury et al. 2008; Bryant et al. 2010). However, such corrections require knowledge about demographic history and SNP selection scheme and are difficult to generalize among studies (Albrechtsen et al. 2010).

In this study, we modify the method described by Nielsen et al. (1998) using joint estimation of ancestral SFS and divergence time. We demonstrate that, when SNPs are discovered in one or more outgroup populations, our method provides accurate estimates of population divergence times from data with ascertainment bias and does not depend on the demography of the ancestral populations. We also present an algorithm, for estimating a rooted population tree from the estimated pairwise divergence times.

Method and materials

Model

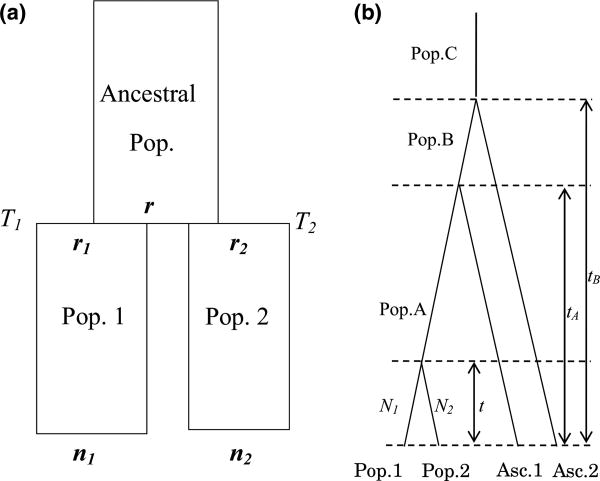
We consider, here, a model (Fig. 1) where two populations (Pop1 and Pop2) diverged from the ancestral population t generations ago as in the methods described by Nielsen et al. (1998). Explanations of the symbols used in the Fig. 1 are given in Table 1, with subscripts indicating population identity. We assume a standard neutral coalescence process, and that loci are di-allelic. Throughout, we use superscript 1 or 2 to label the ancestral and derived alleles, respectively. The data at each SNP site are given by the counts of alleles, ${\mathit{n}}_1=(n_1^1,n_1^2)$ and $n_2=(n_2^1,n_2^2)$ from population 1 and 2, with sample sizes $n_1=n_1^1+n_1^2$ and $n_2=n_2^1+n_2^2$, respectively.

Fig. 1.

(a) The divergence of two populations from an ancestral population. T_i is the scaled divergence time. n_i and r_i are, respectively, the observed and ancestral configurations of the sample in the two populations. (b) Population structure used for data simulation. The two outgroup populations are assigned as the ascertainment populations (Asc. 1 and Asc. 2) and diverged from the focal populations at time t_A and t_B, respectively. The two focal populations (Pop. 1 and Pop. 2, with population size N₁ and N₂, respectively) diverged from their ancestral population (Pop. A) at time t.

Table 1. Notation.

Symbol (i, j = 1or 2)	Notation
Ti	Scaled divergence time, Ti = t/2Ni
nij	Number of jth allele in ith population
ni = (ni1, ni2)	Allele count of samples from ith population
ni	Number of samples from ith population, ni = ni1 + ni2
n	Total number of samples, n = n1 + n2
rij	Number of jth allele ancestral to ith population
ri = (ri1, ri2)	Allele count of lineages ancestral to ith population
ri	Number of lineages ancestral to ith population, ri = ri1 + ri2
rj	Number of jth allele ancestral to all samples, rj = r1j + r2j
r = (r1, r2)	Allele count of all ancestral lineages
r	Number of all ancestral lineages, r = r1 + r2 = r1 + r2

A central assumption is that all SNPs represented in the sample are caused by mutations arising in the ancestral population before the time of population divergence. This assumption is reasonable if T = t/2N is small. It is also justified if the SNPs analysed have been ascertained in an outgroup set of populations that have shared no gene flow with the ingroup populations analysed. We are then interested in estimating the two parameters T₁ and T₂. There are two parameters to estimate as the effective population sizes may differ between the two populations. The resulting estimates of divergence times are, therefore, not symmetric. The likelihood function for a single SNP site can then be written as

$$L(T_1,T_2|{\mathit{n}}_{\mathit{1}},{\mathit{n}}_{\mathit{2}})=\sum _{{\mathit{r}}_{\mathit{1}},{\mathit{r}}_{\mathit{2}}}Pr({\mathit{n}}_{\mathit{1}}|{\mathit{r}}_{\mathit{1}})\mathit{\text{Pr}}({\mathit{n}}_{\mathit{2}}|{\mathit{r}}_{\mathit{2}})Pr({\mathit{r}}_{\mathit{1}},{\mathit{r}}_{\mathit{2}}|r^1,r^2,r_1,r_2)Pr(r_1|n_1,T_1)Pr(r_2|n_2,T_2)Pr(r^1,r^2|r_1,r_2)$$ (eqn 1)

Here, ${\mathit{r}}_1=(r_1^1,r_1^2)$ and ${\mathit{r}}_2=(r_2^1,r_2^2)$ denote the allele counts in the ancestral lineages of the two populations, respectively, at the time of divergence, and r¹ and r² denote the total number of alleles of type 1 and 2, respectively, in the ancestral lineages. $r_1=r_1^1+r_1^2$ and $r_2=r_2^1+r_2^2$ are the numbers of ancestral lineages at the time of divergence in the two populations. The sum in eqn (1) is over all values of $\{(r_1^1,r_1^2,r_2^1,r_2^2)\in N_{+}^4|1\le r_1^1+r_1^2\le n_1,1\le r_2^1+r_2^2\le n_2\}$ and is, therefore, implicitly also a sum over all supported values of r₁ and r₂. The probability of observing the current samples, conditioning on the configuration in the ancestral populations is (Slatkin 1996):

$$Pr\left({\mathbf{n}}_{\mathrm{i}}|{\mathbf{r}}_{\mathrm{i}}\right)=\frac{\left(\begin{array}{c}{n}_i^1-1\\ r_i^1-1\end{array}\right)\left(\begin{array}{c}{n}_i^2-1\\ r_i^2-1\end{array}\right)}{\left(\begin{array}{c}{n}_i-1\\ r_i-1\end{array}\right)}$$ (eqn 2)

In addition, assuming that the probability a gene-copy ends up in one or the other population does not depend on allelic state

$$Pr\left({\mathit{r}}_{\mathit{1}},{\mathit{r}}_{\mathit{2}}|r^1,r^2,r_1,r_2\right)=\frac{\left(\begin{array}{c}{r}^1\\ r_1^1\end{array}\right)\left(\begin{array}{c}{r}^2\\ r_1^2\end{array}\right)}{\left(\begin{array}{c}{r}_1+r_2\\ r_1\end{array}\right)}$$ (eqn 3)

Notice that this assumption will be violated if SNPs were discovered in a population sharing a most recent common ancestral population with one of the ingroup populations more recently than the divergence time of the two ingroup populations. For instance, if the ascertainment population is a sister-population to population one, a rare allele is much more likely to occur in population one than in population two.

The probability of having r₁ and r₂ ancestral lineages at the time of divergence is (Tavare 1984):

$$Pr(r_i|n_i,T_i)=\{\begin{array}{l}{\displaystyle \sum _{k=r_i}^{N_i}{e}^{-k(k-1)T_i/2}}\frac{(2k-1){(-1)}^{k-r_i}{r}_{i(k-1)}{n}_{i\left[k\right]}}{r_i\mathit{!}(k-r_i)\mathit{!}{n}_{i(k)}},2\le r_i\le n_i\\ 1-{\displaystyle \sum _{k=2}^{N_i}{e}^{-k(k-1)T_i/2}}\frac{(2k-1){(-1)}^k{n}_{i\left[k\right]}}{n_{i(k)}},r_i=1\end{array}$$ (eqn 4)

where a_(k) = a (a + 1)…(a + k-1), and a_[k] = a (a-1)…(a-k + 1).

We can now calculate all terms in Equation (1) except Pr(r¹, r² | r₁, r₂). The modification we introduced here is to fully parameterize the ancestral SFS, allowing n parameters, P_n = (p₀, p₁, …, p_n-1), to be jointly estimated from data from multiple loci. Notice that p_n=1−p₀−p₁…−p_n-1. We then obtain

$$Pr\left(r^1,r^2|r_1,r_2\right)=\sum _{i=r^1}^{n-r^2}pi\frac{\left(\begin{array}{c}i\\ r^1\end{array}\right)\left(\begin{array}{c}n-i\\ r^2\end{array}\right)}{\left(\begin{array}{c}n\\ r\end{array}\right)},r^1+r^2=r_1+r_2=r$$ (eqn 5)

We consider here P_n to be a parameter to be estimated and, therefore, we redefine the LHS of Equation (1) as L (T₁, T₂, P_n | n₁, n₂) We refer to this as the fully parameterized method. The advantage of this parameterization is that no information regarding ancestral allele frequencies will affect the estimation of T₁ and T₂. We can take the product of this function over all SNPs and maximize it jointly for the parameters, T₁, T₂ and P_n, using the BFGS (Press et al. 1992) algorithm. If SNPs are located so far apart from each other that they are independent, the estimate is a maximum likelihood estimate. If not, it can be thought of as a composite maximum likelihood estimate.

To compare with the fully parameterized method, we consider two additional models. In the first model, we set the ancestral frequency spectrum to equal the stationary distribution of the Infinite-Sites model at equilibrium $(p_i\propto \frac{1}{i},1\le i\le n-1.)$ We refer to this method as the IS-based method. In a second comparison, we assume the ancestral frequency spectrum follows a Beta-Binomial distribution:

$$p_i\propto \underset{0}{\overset{1}{\int }}\mathit{\text{Bionomial}}(i|n,q)\mathit{\text{Beta}}(q|\alpha ,\beta )dq=\left(\begin{array}{c}n\\ i\end{array}\right)\frac{B(i+\alpha ,n-i+\beta )}{B(\alpha ,\beta )},1\le i\le n-1$$

where B (…) is the beta function and obtain joint maximum likelihood estimates (MLEs) of the divergence times and the parameters of the underlying Beta distribution (α and β). We refer to this method as the Beta-binomial method. The Beta distribution provides some flexibility (but less than what the fully parameterized method offers) in modelling the ancestral SFS. We estimate the divergence time using both the IS-based method and the Beta-binomial method as well, and compare the results with those estimated by the fully parameterized method.

Simulations

To test the performance of our method, we simulated data using a standard neutral coalescent process for diverging populations. We assigned two outgroup populations as ascertainment populations. These two populations diverged from the focal populations (for which we are interested in estimating the divergence time) at 40 000 (t_A) and 100 000 (t_B) years (2000 and 5000 generations, respectively, assuming a generation time of 20 years), which roughly corresponds to the divergence time between Asians and Europeans, and Asians and Africans, respectively. The reason for choosing these times is that we will apply our method to HGDP data and the ascertainment panel of the HGDP is believed to largely consist of Europeans and Africans. Five sequences were simulated from each ascertainment population. These ten samples were pooled together as the SNP discovery panel. Mutations were simulated using the Infinite-Site model with a uniform mutation rate of 10⁻⁶ mutations per locus per year (corresponding to 10⁻⁹ mutations per site per year and a locus length of 1000 bps). Sites showing no polymorphism in the panel were discarded. Data were first simulated as haplotypes and SNPs were then extracted from the haplotypes. As in real data, the SNPs simulated from this process were, therefore, not completely unlinked.

We simulated SNP data using different population sizes, divergence times and migration rates. For a combination of parameters, we simulated 1000 data sets. Each of these data sets includes 100 000 SNPs. Ten samples were simulated from each focal population. We also varied the numbers of SNPs and samples, to test their influence on the performance of our method.

Estimation of trees for asymmetric dissimilarity measures

Notice that the divergence time estimates provided by this method, and other similar methods are asymmetric; the scaled divergence time from population i to the common ancestral population of i and j, T̂_ij, is not in general equal to the scaled divergence time from population j to the common ancestral population of i and j, T̂_ji. The two divergence times are asymmetric because they are scaled with the effective population sizes and the effective population sizes may differ between the populations. As this will be true both for this method and for most other pairwise methods used in population genetics, it is worthwhile to consider how to estimate population trees from such measures. It may be reasonable to require such an algorithm to correctly estimate the tree with correctly estimated additive dissimilarity measures. For example, simply adding T̂_ij and T̂_ji together to form a distance and then applying the Neighbor-joining algorithm (Saitou & Nei 1987) will achieve this. However, we may also reasonably require the algorithm to take advantage of the information in the availability of two asymmetric measures. As the variance in the estimated distance typically increases with the mean, one might reasonably expect that considerable accuracy can be gained by using methods that take advantage of the information from both of the two dissimilarity measures, if the dissimilarity measures are highly asymmetric. In the following, we present one simple algorithm that has these properties:

Initialization

Define C to be the set of leaf nodes, one for each given population, and put L = C.

Iteration

Pick a pair i, j in L for which $D_{ij}=\frac{{\widehat{T}}_{ij}}{M_i}+\frac{{\widehat{T}}_{ij}}{M_j}$, $M_i={min}_{l\ne i}\left\{{\widehat{T}}_{il}\right\}$ is minimal.

Define a new node k and set T̂_kl and T̂_lk for all leaf nodes l (l not equal to i or j) in L as ${\widehat{T}}_{kl}=\frac{1}{2}({\widehat{T}}_{jl}+{\widehat{T}}_{il}-{\widehat{T}}_{ij}-{\widehat{T}}_{ji})$ and ${\widehat{T}}_{lk}=\frac{1}{2}({\widehat{T}}_{li}+{\widehat{T}}_{lj})$, respectively.

Add k to L with edges of lengths T̂_ij and T̂_ji joining k to i and j, respectively.

Remove i and j from L.

Termination

When only one cluster remains.

Notice that the estimated tree is rooted. Also notice the similarity between this algorithm and several other algorithms such as the neighbor-joining algorithm.

East Asian SNP data

We downloaded the HGDP high-resolution genome-wide SNP data (Jakobsson et al. 2008) and extracted the SNP data of 75 individuals (150 chromosomes) from seven East Asian populations (Fig. S1). Our data include 10 Cambodian, eight Lahu, 10 Yi, 12 Han Chinese, 16 Japanese, 10 Daur and nine Mongolian individuals. We did not include individuals from Yakuts because of the worry of possible admixture between Yakuts and European populations (Fig. 1 in Li et al. 2008). We obtained ancestral information for each SNP from the dbSNP database (Sherry et al. 2001) and removed SNPs with unknown ancestral state. We also removed SNPs with more than two alleles and SNPs with missing data. In the end, we analysed more than 475 000 SNPs.

Results

Simulation studies

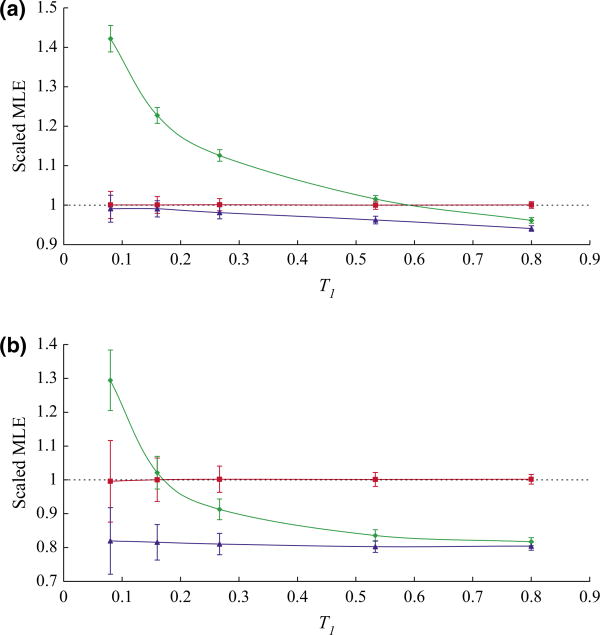
We first simulated data using the population history shown in Fig. 1b. We used the same population size (N₁ = N₂ = 937.5) for both focal populations but varied the divergence times (t) to be 3000, 6000, 10 000, 20 000 or 30 000 years. The corresponding scaled divergence times (T₁ = T₂) were 0.080, 0.160, 0.267, 0.533 and 0.800, respectively. We used an effective population size of 6250 for ancestral populations and ascertainment populations. Ten samples were simulated from each focal population. We applied our method to the simulated data and collected the MLEs. The average running time on a single data set was apporximately 8.5 s on a 2.1 GHz processor. We then calculated the scaled means and standard deviations of the 1000 MLEs (both scaled by the true value of T) and plotted them against the true value of T. We measure the accuracy of the method in terms of the size of the bias and the standard deviation (SD) of the estimates. For the method to perform successfully, we would want both the bias and the SD to be small (bias<5% and SD<10%, for example). As the curves for T₁ are T₂ are highly similar, we only show those for T₁ (Fig. 2a). For all five divergence times, our method provides accurate estimates. In addition, we simulated data using unequal values of N₁ and N₂ and repeated the analysis. We found our estimates to also be accurate under these circumstances as well (Fig. S2).

Fig. 2.

Data were simulated using population structure shown in Fig. 1b with population size N₁ = N₂ = 937.5 and different divergence times ranging from 3000 years to 30 000 years. (a) Ten samples were simulated from each focal population. (b) Two samples were simulated from each focal population. For each combination of divergence time and sample size, 1000 data sets were simulated. Average value of 1000 maximum likelihood estimates was scaled by and plotted against the true value of divergence time, with bars representing scaled standard deviations. Red line represents the result from fully parameterized method. Green line represents the result from IS-based method. Blue line represents the result from Beta-binomial method.

Our method makes inference by jointly estimating divergence times and the ancestral frequency spectrum (P_n). Including the ancestral frequency spectrum explicitly as a parameter in the inference procedure, lends us the ability to account for ascertainment biases introduced when SNPs are detected in outgroup populations. As a comparison, we calculated the scaled average and variance of the 1000 MLEs estimated from the IS-based method and the Beta-Binomial method (Fig. 2a). For the IS-based method, we noticed significant biases in most estimates, illustrating that the ascertainment bias in fact does lead to biased estimates of the divergence time if not accounted for. For small values of T, we observed positive biases. As the value of T increases, the bias decreases and finally becomes negative. In contrast, the estimates found by the Beta-binomial method show little bias (comparable with the fully parameterized method) for small values of T. However, a negative bias can be observed as the value of T increases and is comparable with the IS-based method.

Next, we examined to what extent the choice of sample size and number of SNPs influences the accuracy of our estimates. First, we kept the number of SNPs at 100 000 but simulated only two samples from each focal population. Instead of conducting extra simulation, we reused the data simulated above by randomly picking two samples from each focal population. Our simulation result shows that all three methods generate estimates with larger variances (Fig. 2b) as sample size decreases. This is expected as the data of smaller sample size contains less information. More importantly, we noticed a difference in the pattern of the biases. While the fully parameterized method is only minimally influenced by sample size, the small sample size introduces additional negative biases to estimates from both the IS-based method and the Beta-binomial method. In summary, we conclude that the fully parameterized method performs no worse than the other two methods for any divergence time and can provide accurate inferences for data with small sample size.

Next, we fixed the sample size at two chromosomes per focal population, but varied the number of SNPs to be 30 000, 10 000, 3000 and 1000. Once again, we reused the data simulated before by random sampling SNPs. We plotted the estimates of divergence time against the true values (Fig. S3 two population trees were the same as those shown in) and compared them with results from the full data sets (Fig. 2a). We observed that in most cases, the mean scaled MLEs do not change with the number of SNPs. An exception is that the fully parameterized method tends to find estimates with small negative bias for recent divergence (T = 0.08) from data sets with less SNPs. This bias becomes significant (>5%) for data sets of 1000 SNPs. We also observed that the variance in our estimates increases as we reduced the number of SNPs, similar to the pattern we saw when we reduced the sample size. Furthermore, we found that reducing the number of SNPs from 100 000 to 1000 leads to a bigger variance than reducing the sample size from ten to two. Consider the case where true divergence time equals 0.08 times of the effective population size as an example. Using the fully parameterized method, MLEs estimated from the data set containing two chromosomes per population and 100 000 SNPs have a SD of 12.1%, while those estimated from data sets of ten chromosomes per population with 10 000, 3000 and 1000 SNPs have SD of approx. 10.6%, 20.0% and 40.3%, respectively.

In our model, we assumed no gene flow among populations. Such an assumption helps to simplify and facilitate the likelihood calculation process. However, it also raises questions about our method's reliability, when gene flow is present. While strong gene flow will most likely strongly bias the estimates, we hope our method is less vulnerable to low levels of gene flow. We also want to understand the extent and direction of biases introduced by gene flow. To examine these problems, we simulated three sets of data, each with gene flow between a different pairs of populations. We also varied the population migration rate M (=2Nm). The value of M represents the expected number of migrants per generation.

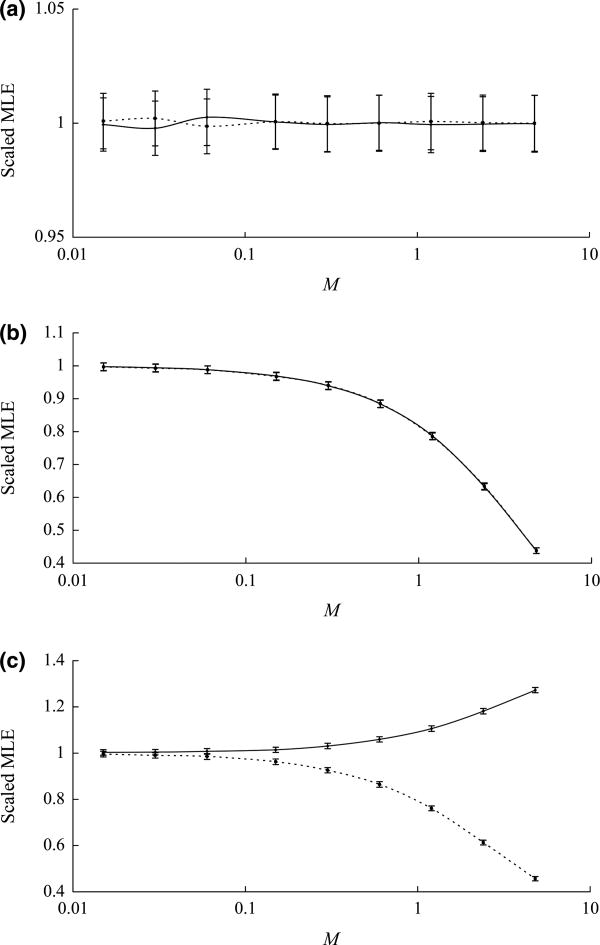
In the first set of simulations, we included gene flow between the ancestral population (Pop. A) and an ascertainment population (Asc. 1). Such gene flow will change the ancestral SFS, but should have no effect on postdivergence drift process. Therefore, we did not observe any significant bias in our estimates (Fig. 3a). Next, we simulated data with gene flow between the two focal populations. The exchange of genetic material between these two populations will reduce the level of divergence. As a result, we found negative biases in the estimates of the divergence time. However, the extent of biases is a function of the geneflow rate (Fig. 3b) and is not significant (<5%) for M <0.15. In the last situation, we modelled gene flow between a focal population (Pop. 2) along with its ancestral population (Pop. A) and an ascertainment population (Asc. 1). Using data simulated from this model, we obtained estimates with biases in both directions (Fig. 3c). In fact, the divergence time along the branch of Pop.1 (T₁) is always overestimated, while that along the branch of Asc. 1 (T₂) can be either overestimated or underestimated, depending on other demographic parameters (results not shown here). Similarly, the extent of biases increases as the level of gene flow increases, but it is minimal (<5%) for small values of M (<0.15).

Fig. 3.

Data were simulated using population structure shown in Fig. 1b with different migration patterns. (a) Migration between Pop. A and Asc. 1. (b) Migration between Pop. 1 and Pop. 2. (c) Migration between Pop. 2 and Pop. A, and Asc. 1. Population migration rates range from 0.015 to 4.8 migrants per generation. For each combination of migration pattern and migration rate, 1000 data sets were simulated. Scaled average of 1000 maximum likelihood estimates was plotted against the migration rate, with bars representing scaled standard deviations. Solid line represents the estimate of T₁. Dot line represents the estimate of T₂.

In many population studies, researchers are interested in the divergence process of many populations in which case the population tree becomes the centre of interest. As optimization over large trees is extremely computationally demanding, methods for estimating trees based on pairwise comparisons become more attractive, and we will focus on one such method. The method is based on first estimating the asymmetric dissimilarity measure T_ij, for all i ≠ j. We use the name ‘asymmetric dissimilarity measure’ because T_ij is not symmetric and is therefore not a distance according to standard mathematical definitions. T_ij, is also not explicitly proportional to the divergence time between population i and j. Instead, it represents the summation of lengths of all branches that lead from population i to the most recent ancestral population of population i and population j, scaled by the population sizes associated with each branch. Subsequently, to the estimation of T_ij and T_ji for all pairs of populations, the population tree can be estimated using standard algorithms based on distances formed as functions of the asymmetric dissimilarity measures. We also explored a new algorithm described in the Methods section that explicitly attempts to take advantage of the information regarding asymmetry in the dissimilarity measures.

To examine the properties of these methods, we simulated data using two population histories, each includes seven focal populations and two outgroup ascertainment populations. In both cases, we used the same outgroup divergence times and population sizes as in the previous simulations. We set other population sizes and divergence times so that the two population trees were the same as those shown in Fig. 4(a,b) Tian, which represent the East Asian population trees estimated using two different algorithms (see section Population tree of seven East Asian populations). In each case, we examined the performance of our method in recovering the assumed ‘true’ East Asian population history. Each data set includes 100 000 SNPs, with five samples from each outgroup population and ten samples from each focal population. 1000 data sets were simulated for each population history.

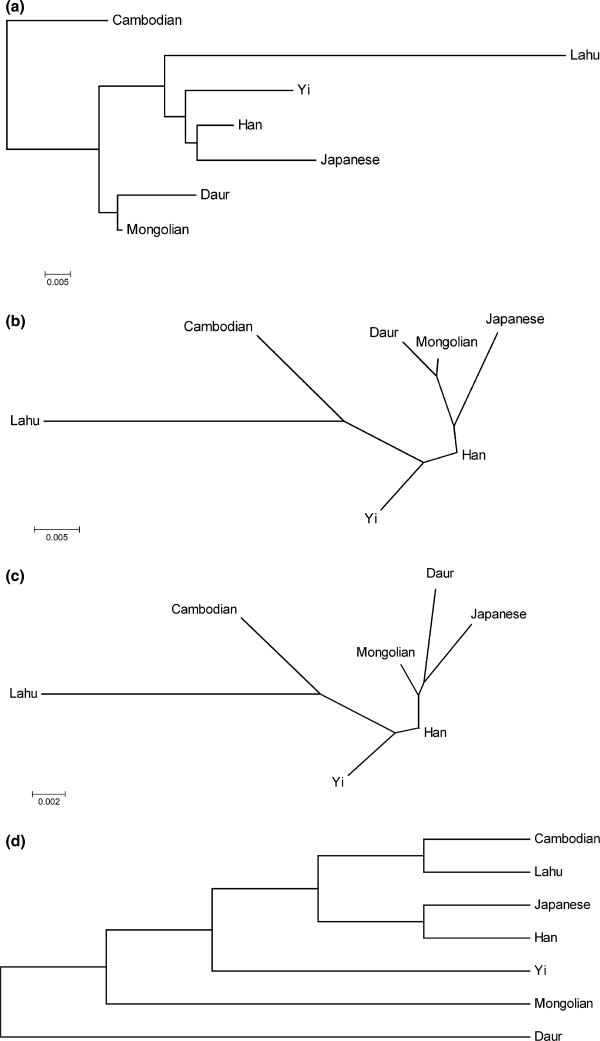
Fig. 4.

(a) Rooted tree estimated from estimates of asymmetric dissimilarity measures, using our algorithm. (b) Unrooted tree estimated from estimates of asymmetric dissimilarity measures, using Neighbor-joining algorithm. (c) Unrooted tree estimated from F_st statistics reported by Tian and colleagues (Tian et al. 2008), using Neighbor-joining algorithm. (d) Rooted tree estimated by Li and colleagues (Li et al. 2008), using the CONTML method in the PHYLIP package.

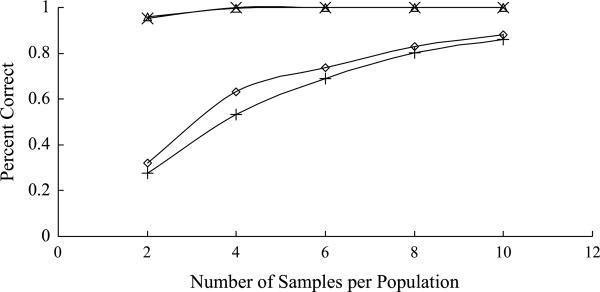
The estimates of the asymmetric dissimilarity measures were plotted against the true value in the simulations (Fig. S4). All points fall near the line x = y, indicating that the estimated asymmetric dissimilarity measures are close to the true values and can be relied upon for estimating population trees. We repeated the simulation for different sample sizes (two, four, six and eight) and estimated population trees from the dissimilarity measures, using both our newly developed algorithm and the Neighbor-Joining algorithm. We counted the number of correctly estimated trees for the two algorithms (Fig. 5). We found both algorithms work well at estimating the population tree in Fig. 4b. Even for small sample sizes, the true tree is recovered with >95% chance. However, the success rate in estimating the other population tree (Fig. 4a) appears to be dependent on the sample size. With a sample size of ten, the true tree is recovered 87.9% and 86.1% of the time by our algorithm and the Neighbor-joining algorithm, respectively. When the sample size drops to two, the percentages of the correctly estimated trees also drop to 32.2% and 27.8%, respectively. However, we notice that for all five sample sizes, the algorithm based on asymmetric measures performed slightly better than the Neighbor-joining algorithm.

Fig. 5.

Data were simulated using two population trees shown in Fig. 4(a,b) with sample size ranging from 2 to 10. For each combination of true population tree and sample size, 1000 data sets were simulated. Population trees were estimated from each data set using our algorithm and Neighbor-joining algorithm. Number of correct trees was plotted against the sample size. Diamond represents the number of correct trees estimated by our algorithm with Fig. 4a as true tree. + represents the number of correct trees estimated by Neighbor-joining with Fig. 4a as true tree. Triangle represents the number of correct trees estimated by our algorithm with Fig. 4b as true tree. x represents the number of correct trees estimated by Neighbor-joining with Fig. 4b as true tree.

Population tree of seven East Asian populations

We applied the methods to genome-wide SNP data of 75 individuals from seven East Asian populations (Jakobsson et al. 2008). We estimated the asymmetric dissimilarity measures between these seven populations (Table 2). We then estimated the population tree using the new algorithm. The resulting tree is drawn in Fig. 4a. We noticed that the population from the Indochinese peninsula (Cambodia) forms an outgroup to the other populations. Of the six remaining populations, Mongolian and Daur form a clade A, and the other four populations form another clade B. Lahu diverge first from the clade B, followed by Yi, leaving Han Chinese and Japanese closely related with each other. We also noticed that some populations have shorter branches than others, possibly due to their larger effective population sizes. For example, Han Chinese has a relative short branch, in agreement with the large size of the population. Mongolian also displays a short branch, which leads us to infer a large Mongolian effective population size. On the other side, Lahu has a very long branch, indicating a possible small effective population size. In addition, we estimated the unrooted tree using Neighbor-joining (Fig. 4b). The unrooted tree differs from our estimated rooted tree in the placement of the Daur-Mon-golian clade. But the two trees show similar lengths for common branches. For comparison, we obtained trees of these seven East Asian populations based on the results of two other studies (Li et al. 2008; Tian et al. 2008). We estimated an unrooted Neighbor-joining tree (Fig. 4c) from the F_st statistics reported by Tian et al. (2008). We also compared with the phylogenetic tree (Fig. 4d, note branch lengths in this figure are not to scale), estimated by Li et al. (2008) using the CONTML method in the PHYLIP package. Notice the similarity between the two Neighbor-Joining trees. Also notice that the unrooted versions of the four trees differ in the placement of Daur and Mongolian populations. The differences between these trees might in part be exacerbated by the presence of gene flow between the populations.

Table 2. Estimated pairwise asymmetric dissimilarity measures between seven East Asian populations.

	Cambodian	Lahu	Yi	Han	Japanese	Daur	Mongolian
Cambodian		0.000	0.002	0.002	0.004	0.014	0.018
Lahu	0.047		0.038	0.039	0.041	0.052	0.056
Yi	0.030	0.011		0.007	0.010	0.018	0.020
Han	0.026	0.009	0.004		0.002	0.012	0.012
Japanese	0.038	0.020	0.016	0.012		0.020	0.022
Daur	0.029	0.013	0.006	0.002	0.000		0.007
Mongolian	0.017	0.001	0.000	0.000	0.000	0.000

Discussion

In this study, we described a maximum likelihood method for estimating divergence times from SNP data with ascertainment bias. In our model, we assumed that the divergence time between the populations is small or that the polymorphic sites used in the focal populations are all detected in a set of outgroup populations. Given either of these assumptions, we argue that mutations occurring after divergence are of little or no influence compared with genetic drift and can be neglected.

In many cases, SNPs genotyped in large samples are first detected in a small discovering panel where they appear to be polymorphic. Consequently, rare alleles are less likely to be included than common alleles, introducing an ascertainment bias. Ascertainment bias results in a skew in the SFS (Clark et al. 2005) and leads to biases in the estimation of genetic variation, population structure, population sizes, migration rates and in population assignment (Morin et al. 2004; Bradbury et al. 2011). Common ways of measuring population divergence from SNP data, like F_ST statistics and principal component analysis (PCA), are likely to be vulnerable to such biases (Albrechtsen et al. 2010). For example, Lewandowska-Sabat et al. (2010) genotyped 282 individuals from 31 Arabidopsis thaliana populations and found a high level of population subdivision (F_ST = 0.85 ± 0.007). However, as the 149 SNPs they genotyped were previously selected to show intermediate global population allele frequencies, their F_ST values are likely to be overestimated. In another study, Seeb et al. (2011) compared chum salmons collected at 114 locations, ranging from Korean and Japan to Alaska and Northern America, by genotyping 60 SNPs discovered in some early efforts that focused on Western Alaska. They saw an elevated level of diversity in Alaska populations reflected in both allelic richness and heterozygosity, which may reflect the intrinsic differences among salmon populations. But they also pointed out the possibility of this being an artefact from ascertainment bias in the SNP panel.

We considered the situation where SNPs are discovered in a set of outgroup populations. We demonstrated that, under these conditions, our method can make fast and accurate inference from data that are strongly affected by ascertainment biases. We also demonstrated that neglecting ascertainment bias (IS-based method) will introduce positive biases for small divergence times and negative biases for large divergence times. A possible explanation is that, for small divergence times, the SFS in both extant populations are very similar to that in the ancestral population. In the IS-based methods, the ancestral SFS is fixed to the expectation of a standard neutral model with infinite-sites mutation. When strong ascertainment biases exist, the true ancestral SFS deviates from the expected one, leading to an upward bias in the difference between the present SFS and the ancestral SFS, which in turn results in the overestimation of divergence times. However, for large divergence times, the SFS in the extant populations are more different from the ancestral SFS because of drift. In the presence of ascertainment biases, the ancestral SFS is enriched for sites with medium frequencies. As the divergence time increases, genetic drift acts to reduce the proportion of medium-frequency sites. Therefore, fixing the ancestral SFS to the expectation of the standard neutral model with infinite-sites mutation introduces a downward bias in the difference between the present SFS and the ancestral SFS, and leads to negative biases in divergence time estimates.

In addition to the IS-based method, we tested a Beta-binomial method that employs a Beta distribution as the ancestral SFS. We noticed that for more recent divergence times, this method is capable of correcting for ascertainment biases caused by SNP discovery in an outgroup sample. However, for large divergence times, the estimates are biased towards smaller values. Moreover, the method does not perform well for data with small sample sizes.

Our method is developed for analysing genome-wide SNP data and may lose its power when applied to smaller data sets. We examined the influence of sample size and number of loci on our estimates through simulation. Interestingly, we found that accurate inferences can still be made from a data set of 100 000 SNPs that includes only two chromosomes from each focal population. Such a result suggests that our method could be used for estimating divergence times from single individuals, a promising prospect with the emergence of individual full genome sequencing. However, the accuracy of our method deteriorates as the number of SNPs included in the analysis decreases. If the number of SNPs is reduced to 3000, the standard deviation increases to about 20% of the true value for very small divergence times. This suggests that our method should be applied to large data set (>10 000 SNPs), when the populations to be studied diverged only recently. However, the standard deviation in the divergence time estimates decreases quickly as the divergence time increases. For example, as the divergence time increases to 0.16 times of the effective population size, the standard deviation will drop to about 12%. Moreover, we noticed that higher variance in divergence time estimates does not necessarily lead to worse population trees. The accuracy in estimating some population histories (for example, the one in Fig. 4b) is less sensitive to the standard deviation in the divergence time estimate, possibly due to the lack of short internal branches. Combining these observations, we suggest that our method may be applied to data set with <10 000 SNPs, if divergence times are relatively large compared with the effective population sizes. But the results should be taken with some caution.

In this study, we also described a new algorithm for estimating rooted population trees from asymmetric dissimilarity measures. The algorithm uses a distance-based method to reconcile the divergence times estimated from each pair of populations. The algorithm is, therefore, the first population/species distance-based method for estimating species / population history. We compared this algorithm with the Neighbor-Joining method based on simple addition of the dissimilarity measures. The new algorithm generally performs better than the Neighbor-Joining algorithm, suggesting that further research into algorithms for estimating trees from asymmetric dissimilarity measures is warranted. The algorithm we presented has some advantages shared with the Neighbor-Joining method, such as provable consistency, but there may be other algorithms with better statistical properties for solving this problem. In addition, the use of Neighbor-Joining might be improved for these applications by using other functions than simple addition for converting asymmetric dissimilarity measures into distances.

With the fast advances in new-generation sequencing technologies and high throughout genotyping platforms, the volume of available genome-wide SNP data is rapidly increasing, in humans and many other organisms. Commercial high-density SNP chips are now available for chicken, cattle, dog, pig, sheep, horse, mouse and maize, all of which include at least 50 000 high quality SNPs. Genome-wide surveys of SNP variation have also been performed in many plants (McNally et al. 2009; Hohenlohe et al. 2010; Geraldes et al. 2011). We are foreseeing a growing trend of using large, gen-ome-wide data for population genetics and phylogenetic analyses. For such data, the methods developed here should be of use.