Surface shear inviscidity of soluble surfactants

Significance

Why some surfactant molecules promote long-living foams, while others are low foamers, remains mysterious. Experiments over the past 60 y have suggested that a surfactant’s surface shear viscosity (η_S) is correlated with the stability of the foam it produces, giving a widely held rule of thumb for foaming surfactants. Published η_S measurements for the heavily studied foaming surfactant sodium dodecyl sulfate (SDS), however, show almost no agreement, motivating a critical reevaluation. Using ferromagnetic microbutton probes, we perform the most sensitive and precise η_S measurements to date on SDS and a wide variety of soluble, small-molecule surfactants spanning different molecular characteristics and foamability. In fact, all soluble surfactants were found to have immeasurably small η_S, undercutting evidence for η_S–foam stability correlations.

Abstract

Foam and emulsion stability has long been believed to correlate with the surface shear viscosity of the surfactant used to stabilize them. Many subtleties arise in interpreting surface shear viscosity measurements, however, and correlations do not necessarily indicate causation. Using a sensitive technique designed to excite purely surface shear deformations, we make the most sensitive and precise measurements to date of the surface shear viscosity of a variety of soluble surfactants, focusing on SDS in particular. Our measurements reveal the surface shear viscosity of SDS to be below the sensitivity limit of our technique, giving an upper bound of order 0.01 μN·s/m. This conflicts directly with almost all previous studies, which reported values up to 10³–10⁴ times higher. Multiple control and complementary measurements confirm this result, including direct visualization of monolayer deformation, for SDS and a wide variety of soluble polymeric, ionic, and nonionic surfactants of high- and low-foaming character. No soluble, small-molecule surfactant was found to have a measurable surface shear viscosity, which seriously undermines most support for any correlation between foam stability and surface shear rheology of soluble surfactants.

Surfactants facilitate the formation of foams and emulsions by reducing surface tension, thereby lowering the energy required to create excess surface area (1–3). These multiphase materials, however, are thermodynamically unstable, and coarsen through bubble or drop coalescence, as well as diffusive exchange between bubbles or drops (1, 4–6). Surfactants can additionally be used to control this coarsening rate, with effective foaming surfactants retarding coalescence, and defoamers speeding it. For example, coalescence may be slowed by repulsive forces between the surfactant monolayers adsorbed to either side of the (continuous) phase separating bubbles or drops. Ionic surfactants, for example, introduce electrostatic repulsions (1, 2, 5), whereas nonionic surfactants (e.g., polymers, proteins, or particles) provide steric barriers against coalescence (7–9). Moreover, Marangoni stresses arise when compressional or dilatational deformations drive gradients in surfactant concentration (and thus surface tension). The resulting dilatational surface elasticity resists surface area changes, slowing drainage and rupture of the thin fluid films between adjacent bubbles (4, 5, 10–13).

Additionally, surfactant monolayers may exhibit nontrivial rheological responses. For example, the surface shear viscosity η_S gives the excess viscosity associated with shearing deformations within the 2D surfactant monolayer. Because surfactant interfaces are inherently compressible, they may exhibit a surface dilatational viscoelasticity η_D*, in addition to η_S*, even under small-amplitude deformations. This contrasts with incompressible Newtonian liquids, which are well-described by a single scalar viscosity. Moreover, surface shear and dilatational viscosities need not have equal (14), or even comparable, magnitudes, because they arise due to physically distinct mechanisms. Finite adsorption–desorption kinetics from a compressing–dilating surface, for example, are inherently dissipative, and act effectively like a surface dilatational viscosity (15, 16).

Over the past 60 y, a widespread belief has developed that the surface shear viscosity η_S promotes foam stability (17). Correlations between foam stability and η_S have been reported for a variety of small-molecule surfactants, using various measurement techniques (18–25). Such correlations, if true, would have tremendous significance, because specialty surfactant mixtures could be designed for foaming (or defoaming) applications by targeting a single quantity (η_S), akin to viscosity-matching liquid blends. Nonetheless, pinning down these correlations has remained elusive (26).

The putative correlation is based on numerous experiments involving small-molecule surfactants (18–25), in which foam stability and surface shear viscosity η_S were measured as functions of some solution variable, and observed to be correlated. Although physical mechanisms have been postulated by which η_S could enhance foam stability [e.g., by reducing foam drainage or rupture rates (4, 5, 17)], it is significant that all measured relations have been correlative, rather than causative. It is entirely possible that increasing η_S neither enhances nor impacts the foam stability directly, but simply that both quantities are impacted by some other property (e.g., structural or surface dilatational rheology) which is changing with the solution.

Moreover, even the interpretation of surface rheology measurements can be very subtle, as evidenced by thousand-fold variations among published η_S measurements for the soluble surfactant SDS (27). Considering the excellent foaming properties of SDS, and its ubiquity in the scientific literature, definitive and reliable measurements of its surface rheology will directly impact any putative correlation between foam stability and surface shear viscosity.

Here, we report the most precise, sensitive measurements to date of the surface shear rheology of SDS. Surprisingly, our measurements unambiguously reveal the surface shear viscosity to be immeasurably small, with an upper bound of η_S < 0.01 μN·s/m. This conflicts directly with the significantly higher values reported previously. The technique, described below, is certainly sensitive enough to measure surface viscosities of the magnitudes reported in the literature; nonetheless, our measurements on SDS interfaces are consistently subphase-dominated. We performed multiple complementary control experiments, which unambiguously reveal the interface to be sheared as we expect, yet which consistently show no trace of any surface shear viscosity, much less of the magnitudes reported previously.

In fact, we tested 23 different soluble small-molecule surfactants, chosen to include ionic, nonionic, and polymeric species, comprising both high- and low foamers (SI Appendix, Table S1), and found all to have immeasurably small surface shear viscosities. This stands in stark contrast with our measurements on insoluble surfactants [both eicosanol, described below, and phospholipids (28–30)]. Given the foaminess of SDS, and the range of soluble surfactants tested here, the lack of any measurable surface viscosity calls into serious question any correlation between surface shear viscosity η_S and foam stability for soluble, small-molecule surfactants.

We begin with a brief description of the active, interfacial microrheometry technique (Fig. 1A). Ferromagnetic microbuttons of 10- and 50 μm radius, 2- and 10 μm height, and buttonholes of 3- and 15 μm diameter, were fabricated using photolithography as described previously (31), with thin layers of nickel (150 nm) and gold (10 nm) added via electron beam physical vapor deposition to impart an in-plane ferromagnetic moment and Janus amphiphilicity via fluorocarbon–thiol self-assembled monolayers (Fig. 1C). Two orthogonal pairs of electromagnets are placed within a custom-designed aluminum sample holder (Fig. 1B), which can serve as a stand-alone container for soluble surfactant solutions, or inserted into a Langmuir trough for insoluble (spread) monolayers. The rotational displacement (strain) of a microbutton held at the liquid interface within the surfactant monolayer is measured in response to an externally applied torque (stress) imposed by the electromagnets, from which surface shear rheology is determined (28–30, 32).

Fig. 1.

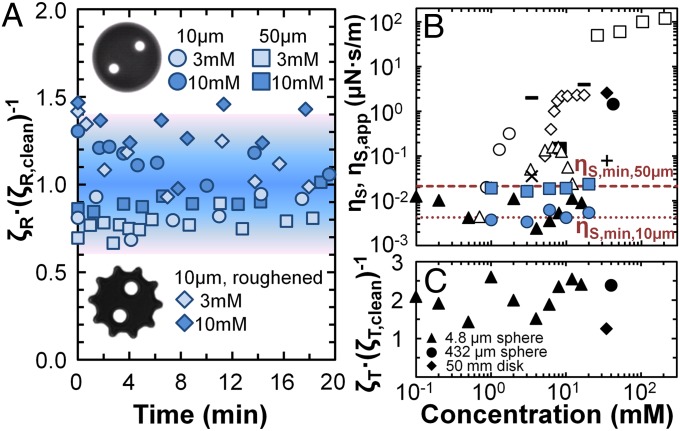
(A) Experimental setup for microbutton surface rheometry consists of a sample–electromagnet holder placed within a Langmuir trough, a Wilhelmy plate for surface pressure measurements, and bright-field microscopy using a zoom lens and CCD camera; (B) electromagnet and sample holder where microbuttons are added; (C) bright-field image of a 10-μm microbutton. (D) Rotational resistance ζ_R measured at clean air–water surfaces versus oscillation frequency. Subphase drag for 10-μm probes is 5³ = 125 times smaller than for 50-μm probes.

Microbuttons are visualized in bright field using a motorized zoom lens microscope (Navitar 6.5×) resting upon a motorized XYZ stage (ThorLabs). Images are acquired with a camera (JAI CV-A10) and frame grabber (NI PCI-1428). A data acquisition (DAQ) device (NI PCIe-6353) controls the analog voltage output to a linear amplifier (Sony STR-DH100 or Rheomics RTA), which drives a current through a pair of electromagnets surrounding the cone, generating a uniform magnetic field within the area of interest. This exerts a torque |L| = mB₀ sin(θ_B − θ_m) on the probe, where θ_m and θ_B are the orientations of the magnetic moment m and the applied B field, respectively. Applying B perpendicular to m gives a torque well-approximated by L₀ ∼ mB₀. A custom LabVIEW code interfaced with the frame grabber and DAQ hardware records the microbutton orientation (via buttonhole tracking) and applied torque simultaneously.

Measuring the angular displacement (Δθ₀e^i(ωt-δ)) of a circular microbutton under an oscillatory torque (L₀e^iωt) gives the rotational resistance

The resistance ζ_R of a rotating disk within a surfactant interface depends upon both the surface shear viscoelasticity η_S and the subphase viscosity η (33). The relative magnitude of interfacial viscous drag to the subphase (bulk) contribution is given by the Boussinesq number,

where a is the disk radius. Reliable measurements of η_S are best performed in the Bo >> 1 (surface-dominated) limit, where ζ_R*(ω) is given by

In the absence of surfactant (Bo = 0), or in the Bo << 1 limit (where the subphase fluid dominates the drag on the disk), the resistance is given by

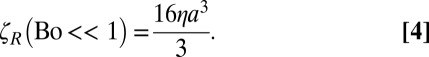Indeed, ζ_R for 10- and 50-μm microbuttons on a clean water subphase are measured to be frequency-independent and to obey Eq. 4 quantitatively (Fig. 1D).

Drag from the subphase imposes a lower limit on the surface viscosity that can be measured accurately using a probe of radius a. We define this sensitivity limit as the apparent surface viscosity η_S,app that would be inferred if the rotational resistance ζ_R measured on a clean subphase (Eq. 4) were interpreted as surface-dominated (Eq. 3), giving

corresponding to η_S,app = 0.0042 μN·s/m for a 10-μm probe on a water subphase. This sensitivity limit implies that O(0.01 μN·s/m) surface shear viscosities can be resolvable unambiguously, whereas smaller surface shear viscosities would change the relative resistance ζ_R/ζ_R,clean by O(1) or less. The ferromagnetic microbuttons used here are among the most sensitive probes of interfacial rheology, compared with other directly forced probes [e.g., interfacial shear rheometer (ISR, 1 μN·s/m), double-wall ring (5 μN·s/m)] or indirect interfacial forcing techniques [e.g., deep-channel surface viscometer 0.1 μN·s/m or knife-edge viscometer 0.01 μN·s/m] (17, 34, 35). Whereas torqued magnetic nanorods (36, 37) and passive (colloid-tracking) microrheology (38, 39) have nominally higher sensitivity O(0.001 μN·s/m), they excite mixed rheological deformations (i.e., shear, extension, and compression), and thus combine multiple distinct properties into one measured quantity. It is very difficult to extract η_S from rheologically mixed flows, especially in the Bo ∼ 1 limit.

Having described the technique and its advantages, we now describe surface shear rheology measurements of soluble surfactants. Although we focus our detailed discussion on SDS solutions, motivated by the many η_S measurements (27) that have been published using various techniques, we have made analogous measurements on over 20 soluble, small-molecule surfactants, with identical results (SI Appendix, Table S1). Direct drag measurements have been reported for SDS using translating or rotating probes (18, 40–43). Indirect methods externally impose a subphase flow, measure the surface flow field using tracer particles, and deduce η_S using a hydrodynamic calculation (14, 25, 44, 45). Finally, values for η_S have been inferred from foam drainage experiments (46, 47), generally by making some assumption about the relative magnitudes of η_S and η_D.

Solutions of SDS (Fisher Scientific, purified via one recrystallization from ethanol–toluene solution) were prepared in deionized water (Millipore, 18 MΩ·cm) with concentrations ranging above and below the critical micelle concentration (CMC, ∼8 mM). Samples were used within several hours of preparation to minimize hydrolysis of SDS into dodecanol (48). Solution was placed into the aluminum sample holder (Fig. 1B), a microbutton was then deposited onto the surface, and ζ_R* was measured (f = 1 Hz, Δθ₀ ∼ 0.05 rad) over time to allow for adsorption equilibration (Fig. 2A) (48, 50, 51).

Fig. 2.

(A) Rotational probe resistance ζ_R, normalized by the resistance on a clean air–water surface, measured on SDS interfaces as a function of time. The rotational resistance is subphase-dominated for concentrations below and above CMC, using 50-μm (blue squares) and 10-μm (blue circles) circular probes and roughened 10-μm (blue diamonds) probes. The shaded background reflects an ∼40% uncertainty in the magnetic moment of the microbuttons, and thus the measured ζ_R. (B) Previous measurements of the surface shear viscosity of SDS have used direct [closed: ● (40), ◆ (41), ▲ (42) ■ (43), ▂ (18)], and indirect forcing [open: ◆ (44), ■ (45), ● (25), ▲ (14)], and inferred values from foam drainage experiments [x (46), + (47)]. [Surface shear viscosity values were inferred from drag coefficients measured by Ally and Amirfazli, ref. 42, using the theory of Danov et al. (49).] Notably, measured η_S values differ dramatically from one technique to another, with thousand-fold variations measured at various concentrations. Microbutton measurements (blue) reveal SDS surface viscosity to be below the sensitivity limits of the microbutton as η_S,app ∼ η_S,min. (C) Translational probe resistance ζ_T, normalized by ζ_T,clean, in previously published direct drag measurements (40–42) is always O(1), despite probe sizes varying over factors of 10³–10⁴. This is inconsistent with the influence of η_S as an intrinsic material property (Eq. 10).

Fig. 2A shows ζ_R, normalized by the subphase-dominated drag (ζ_R,clean ∼ 16η_watera³/3), to be essentially unity, for concentrations above and below the CMC, indicating that the surface shear viscosity of SDS exerts a negligible contribution on the rotational drag of both 50- and 10-μm microbuttons. In fact, any apparent η_S values inferred from these measurements would depend on the microbutton size (Fig. 2B), an interpretation that would obviously be inappropriate. This subphase-dominated response stands in stark contrast with previous measurements (Fig. 2B), most of which have reported a surface shear viscosity η_S for SDS that is well above the microbutton’s sensitivity limit, and which would therefore be easily resolved by the microbutton.

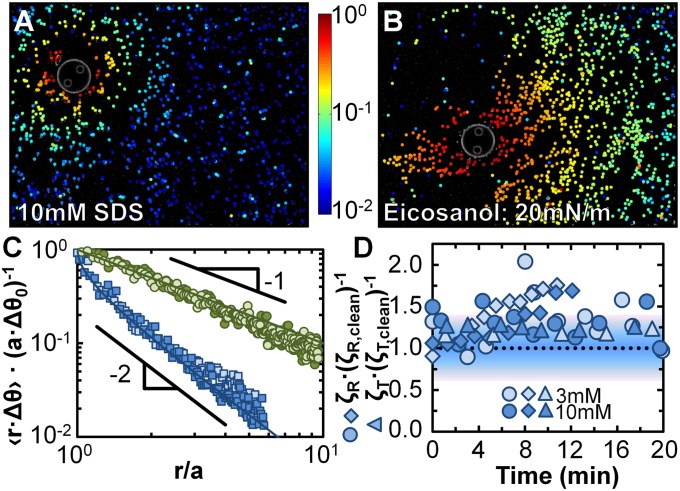
The discrepancy between measured values of η_S for SDS obtained using the microbutton versus previous techniques is dramatic, and naturally calls the microbutton measurements into question. We thus performed multiple complementary control experiments to ensure that the microbutton did indeed shear the monolayer as assumed, and that the interpretation was accurate. Strain sweeps showed no dependence on strain amplitudes from ∼0.01 to 0.3 rad (SI Appendix, Fig. S1), alleviating concerns of a nonlinear response (e.g., strain softening or yielding). We performed several controls to ensure that the microbutton did not slip relative to the SDS interface, because slip would cause ζ_R to be artificially low. First, we made 10-μm gear-shaped microbuttons (Fig. 2A), analogous to roughened rheometer plates, to ensure the probe engages the interface. Even for roughened probes, the relative ζ_R was measured to be O(1) and thus subphase-dominated. Second, we added interfacially active colloids to SDS solutions (both above and below CMC), and tracked their motion as the microbutton oscillated (Fig. 3A). The azimuthal displacement field on the surface of both 3- and 10-mM SDS solutions decays with distance like r⁻², as expected for subphase-dominated flows (52) (Fig. 3C), and matches the microbutton boundary velocity precisely, revealing no measurable slip. These measurements, along with the measured O(1) 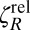(Fig. 3D), prove unambiguously that the microbutton shears the SDS monolayer as we have assumed, and therefore confirm our interpretation that η_S for SDS solutions must lie below the η_S ∼ 0.01 μN·s/m sensitivity limit.

Fig. 3.

Visualization of surface flow fields during oscillatory rheology experiments. Colormap images show the averaged, normalized azimuthal displacement amplitude r Δθ of interfacial tracer particles, normalized by the displacement amplitude aΔθ₀ of the microbutton boundary, as a 50-μm microbutton is driven into gentle rotational oscillations, on (A) a 10-mM SDS solution and (B) an insoluble, viscous eicosanol monolayer (Π ∼ 20 mN/m). (C) On both monolayers, the measured surface velocity matches the microbutton velocity at the boundary. The velocity profiles decay differently for SDS monolayers (for which v_θ ∼ r⁻², as expected for surface-dominated monolayers) and eicosanol monolayers (for which v_θ ∼ r⁻¹, as expected for surface-dominated monolayers). Blue markers represent SDS monolayers (light blue squares: 3-mM SDS, Δθ₀ = 0.15 rad; dark blue squares: 10 mM, Δθ₀ = 0.15 rad), and green markers eicosanol (light green circles: Π = 20 mN/m, η_S = 4 μN·s/m, Δθ₀ = 0.04 rad; dark green circles: Π = 35 mN/m, η_S = 3 μN·s/m, Δθ₀ = 0.03 rad). Solid lines represent theoretical predictions (52) for high- and low Bo. Particle adsorption, evident from Movies S1 and S2, increases the effective microbutton radius, more for SDS (∼2–3 particles) than for eicosanol (1 particle). Velocity decay (r⁻² vs. r⁻¹) is unaffected by effective radius. (D) Rotational resistance (ζ_R, diamonds, normalized by ζ_R,clean) measured during particle-tracking experiments for SDS solutions are O(1), confirming the subphase-dominated response. For comparison, normalized rotational and translational resistance (ζ_R, circles and ζ_T, triangles) measured simultaneously with 10-μm microbuttons for 3- and 10-mM SDS solutions, are also all subphase-dominated. The shaded background reflects an ∼40% uncertainty in the magnetic force, and thus the measured ζ.

Because microbutton rheometry has not been validated quantitatively against existing techniques, one might question the quantitative comparisons made here. [Previous microbutton measurements of insoluble phospholipid monolayers (28–30) showed η_S > η_S,min, yet no complementary measurements had been published to compare.] To validate the microbutton’s quantitative capabilities, we measured monolayers of 1-eicosanol on air–water interfaces, for which measurements using the well-established ISR have been published (35, 53). We spread 1-eicosanol (Sigma-Aldrich) from a chloroform solution (EMD Chemicals) onto deionized water (Millipore, 18.2 MΩ·cm) in a Langmuir trough. The surface pressure–area (Π–A) compression isotherm (Fig. 4, Inset), measured with a Wilhelmy plate (R&K), shows two distinct phases, known to be a tilted L₂′ phase at low surface pressures and an untilted L_S,I phase above ∼15 mN/m (35, 53). A 10-μm microbutton is added to the interface at a low surface pressure, and the surface is compressed to the desired surface pressure. Fig. 4 (Inset), taken at 30.8mN/m, shows a typical surface shear rheology measurement in the L_S,I phase: ζ_R is ∼10³ times above the sensitivity limit, and the response is essentially Newtonian, with G_S″ > G_S′ and G_S″ ∼ f^0.91. Measuring η_S = G_S″/ω at f = 1 Hz while sweeping surface pressure reveals both qualitative and quantitative agreement with published ISR measurements (35, 53). Furthermore, η_S ∼ 10³–10⁴ η_S,min, confirming the interfacially dominated (Bo >> 1) limit.

Fig. 4.

Surface shear viscosity of an insoluble monolayer of 1-eicosanol is 10³–10⁴ higher than the sensitivity limit for the 10-μm microbutton (dotted line) at all surface pressures. The surface shear viscosity measured by the microbutton (●) agrees qualitatively and quantitatively with previously reported interfacial shear rheometer measurements (+) [ISR (53)]. (Left, Inset) Surface pressure–area isotherm of a 1-eicosanol monolayer on the air–water interface shows an L₂′ phase at low surface pressures, with a phase transition to an untilted L_S,I phase at ∼15 mN/m. (Right, Inset) At Π = 30.8 mN/m, a frequency sweep of surface shear elastic (G_s′) and loss (G_s″) moduli shows viscous-like behavior.

Finally, we used particle-tracking measurements of eicosanol monolayer deformation (Fig. 3B) to highlight the qualitative distinction between high- and low-Bo systems. As with SDS, no slip occurs between the microbutton and the surfactant monolayer. Unlike SDS, however, surface velocity profiles in eicosanol decay like r⁻¹ (Fig. 3C), as expected for interfacially dominated (Bo >> 1) rotational flows (52).

The quantitative agreement between the microbutton and ISR measurements for the (insoluble) eicosanol monolayer validates the quantitative capabilities of microbutton measurements. Multiple control experiments proved SDS monolayers to be sheared without slip, with strain fields that decay in a clearly subphase-limited manner, and with immeasurably small surface viscosity. The strong discrepancy between published results and microbutton measurements for SDS necessitates a closer examination of previous results, particularly because this surface shear inviscidity was not limited to SDS, but in fact held for every soluble, small-molecule surfactant we tested.

Traditional bulk rheometers use specifically designed geometries that excite pure shear deformations, to measure shear rheology without extensional (or rheologically mixed) deformations. Interfacial rheology faces the additional complications of dilatational deformations, as well as continuous adsorption–desorption of soluble surfactants. One cannot unambiguously extract a surface shear viscosity η_S from any measurement that mixes surface deformations. Rotating circular microbuttons (Fig. 1C) were specifically designed to establish pure shear deformations (28, 32), thereby avoiding the complications of rheologically mixed flows.

Translating probes, for example, deform the surface via compression, dilation, and extension, in addition to shear. Fischer (54, 55) emphasized that a surfactant’s response to these compressional deformations increases a probe’s translational resistance (ζ_T = F/U) above its value on a surfactant-free surface, even for completely inviscid surfactants. The resistance ζ_T of a disk translating on a clean, surfactant-free subphase (56) is given by

whereas the resistance of the same disk translating on a surfactant-laden (incompressible) but surface shear inviscid, (η_S = 0) interface is (33)

Merely adding a surfactant to the interface––even for which η_S = 0––changes the relative translational resistance ,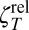

by an O(1) amount. It is thus extremely challenging to reliably extract a surface shear viscosity η_S when the relative drag is O(1). By contrast, a translating disk in the interfacially dominated limit (Bo >> 1) has resistance

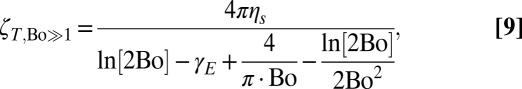whose magnitude vastly exceeds the ζ_T ∼ η·a inherent in subphase-dominated systems (33), thus giving a relative drag ,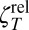

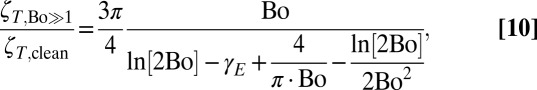which is large (∼Bo) in the Bo >> 1 limit.

Experiments that use translating probes to interrogate surface rheology therefore give clear results only when interfacial drag dominates (ζ_T/ζ_T,clean ∼ Bo >> 1). It is much more difficult to extract surface shear viscosities when relative drag coefficients ζ_T/ζ_T,clean are measured to be O(1), as even small measurement uncertainties or errors Δζ_T would give an apparent η_S ∼ η·a·Δζ_T even on an inviscid interface. Because an intrinsic material property like η_S must not depend on the size of the probe used to measure it, experiments with multiple probe sizes would provide a check for consistency among results. Analogous controls for probe size effects are standard practice in particle-tracking microrheology (57). Any η_S that was truly responsible for O(1) changes to the relative drag ζ_T/ζ_T,clean of a translating 432-μm probe (40) must cause O(100) changes in the relative drag of translating 4.8-μm probes (42). All direct measurements of probes translating within SDS interfaces (40–42), however, found relative drag coefficients of order unity, irrespective of the probe size (Fig. 2C). Such results are inconsistent with interpretations of an intrinsic surface shear viscosity.

As a final, complementary check on our findings, we measured the translational resistance ζ_T of microbuttons within SDS and eicosanol monolayers (SI Appendix, Fig. S2). An applied magnetic field gradient exerts a force F_mag = m⋅∇B on the microbutton, whose translational velocity U is measured to obtain a translational resistance, ζ_T = F_mag/U. Fig. 3C shows the normalized ζ_R and ζ_T for 3- and 10-mM SDS solutions, measured simultaneously, as functions of time. Unlike the viscous eicosanol monolayer, for which ζ_T/ζ_T,clean ∼ 10³ (SI Appendix, Fig. S3), the relative translational resistance ζ_T/ζ_T,clean ∼ O(1) on all SDS interfaces, consistent with rotational ζ_R/ζ_R,clean results.

All evidence—small-amplitude oscillatory rotation and translation––thus supports the conclusion that the surface shear viscosity of SDS is below the sensitivity limit (∼0.01 μN·s/m) of 10-μm microbuttons. Roughened microbutton probes, as well as direct visualization of the interfacial strain field, unequivocally rule out slip between the probe and the monolayer, and directly confirm the monolayer is sheared as expected. Although our results contrast directly with a long-standing body of published measurements, they have been rigorously tested with multiple, complementary control experiments. Furthermore, this surface shear inviscidity is not limited to SDS, but rather was found for all small-molecule surfactants tested––comprising ionic, nonionic, and polymeric molecules of both high- and low-foaming character. We therefore hypothesize that our central result will hold more generally, and that the surface shear viscosity of soluble, small-molecule surfactants is generally below the measurement limits of current techniques. In light of these findings, we naturally question the existence of foam stability–η_S correlations for this group of surfactants.

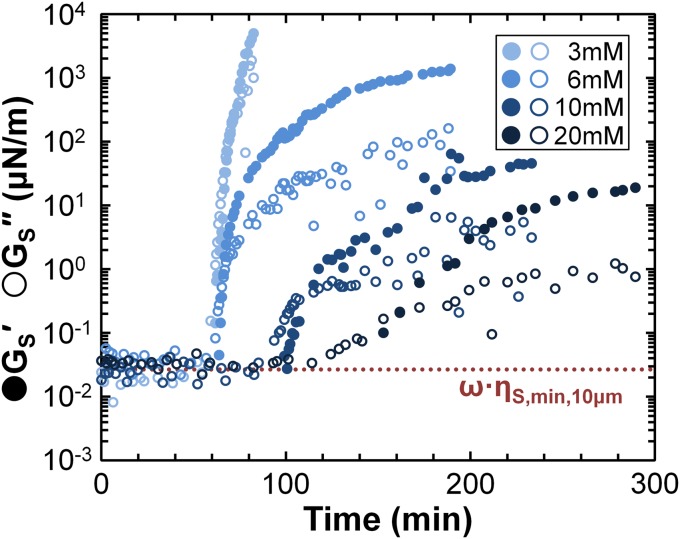
Impurities may also contribute to the large variations in some previous SDS η_S measurements (Fig. 2B). In fact, we observed the surface shear moduli (G_S′, G_S″) of SDS to exhibit an unexpected and dramatic increase (Fig. 5) over time scales much longer than the surface adsorption time. Analogous aging has been measured with oscillating Du Nuoy rings after ∼35 min (58), and in suspended soap films after ∼6 h (43). Mixed solutions of SDS and lauric acid showed significant aging in surface viscosity measurements (59). Under our conditions, SDS surfaces exhibit a structureless fluid phase (60, 61), so that the aging in Fig. 5 implicates phenomena beyond simple evolution. One possibility for SDS involves 1-dodecanol contaminants, from either the original synthesized material or from hydrolysis of SDS in aqueous solution. Condensed, dodecanol-rich domains have been observed during the adsorption of mixed dodecanol–SDS solutions (60, 61). Similarly, insoluble fatty acids can be solubilized within micelles of soluble surfactants, but gradually accumulate at fluid interfaces to form rigid, condensed domains that stiffen the interface (62). More generally, subunits can complex to form extended structures––e.g., surfactant–polyelectrolyte complexes can form entangled, gel-like structures at the surface (63), and multivalent cations can effectively cross-link anionic surfactants like fatty acids (64) to drive a measurable surface shear rheology. SDS aging in our experiments appears to involve aluminum cations leaching off of the sample holder, which will be pursued separately.

Fig. 5.

Viscoelastic aging at the surface of SDS solutions: at long times, both the surface shear elastic modulus (filled) and viscous modulus (open), measured at 1 Hz, increase well above the sensitivity limits. As the bulk concentration of SDS increases, the onset of aging is delayed, and the rate of aging decreases.

To summarize, microbutton microrheometry reveals SDS solutions to have surface shear viscosities below a sensitivity limit of ∼0.01 μN·s/m––far lower than previously reported. Immeasurably small surface shear viscosities were measured consistently for all soluble surfactants tested (both above and below CMC) and with all probe modes (rotation and translation of circular and gear-shaped microbuttons). By contrast, microbuttons provide reproducible surface shear viscosity measurements for insoluble surfactants, in quantitative agreement with the published literature. Although not exhaustive, the wide range of soluble, relatively low M_w surfactant species tested here (SI Appendix, Table S1)––including ionic, nonionic, and polymeric surfactants of high- and low-foaming character––strongly supports the hypothesis that soluble surfactants generically exhibit extremely small surface shear viscosities. Competitive adsorption studies indirectly support this hypothesis, as the addition of soluble surfactants typically reduce the measured interfacial shear moduli of adsorbed protein layers [BSA with Tween 80 (65, 66), beta-Lactoglobulin with SDS (58), Tween 20 (67), and pluronic F-127 (68) and biofilms with Tween 20 (69)].

Our results effectively undercut evidence that has long been used to support correlations between multiphase material stability and the surface shear viscosity η_S of small-molecule, soluble surfactants. These results necessitate a critical re-evaluation of η_S–foam stability correlations should be reexamined critically, to determine whether surface shear rheology plays any role.