Sources of Population Aging in More and Less Developed Countries

Populations in all regions of the world are growing older, a development that is having a profound impact on a broad range of economic, political, and social processes. In this article, we investigate the sources of the aging that occurred during 2005–10 in developed and developing countries. We use changes in the mean age of the population as the principal indicator of population aging, but we also consider the sources of growth in the proportion of the population above ages 65, 70, and 75.

Generations of demographers have learned about the determinants of age structure primarily through the prism of the stable population model (Keyfitz 1975; Lee 2011). In developing this model, Sharpe and Lotka showed that a population closed to migration and experiencing a time-invariant set of age-specific fertility and mortality rates would eventually attain a constant rate of growth—positive, negative, or zero—and an age distribution that was also constant over time (Sharpe and Lotka 1911). The characteristics of that stable age distribution could be inferred directly from the fertility and mortality rates that produced it. By comparing stable age distributions produced by different combinations of fertility and mortality regimes, an analyst could connect patterns of fertility and mortality to characteristics of age distributions. In a classic study of age structural determinants using the stable model, Coale (1957) concluded that fertility was a “quantitatively much more important source” of variation in age structure than mortality when account is taken of the range of fertility and mortality observed in the world. Of course, the range of mortality conditions, particularly at older ages, has expanded dramatically since this assessment was made (Oeppen and Vaupel 2002).

The necessary and sufficient condition for stability is a set of age-specific growth rates that are constant over age (Preston, Heuveline, and Guillot 2001). Few contemporary populations meet this condition, a circumstance that caused Keyfitz (1975) to doubt the utility of the model for understanding actual processes of aging. But the stable model provides one central lesson applicable to any population: changes in age distributions cannot be attributed to levels of fertility, mortality, or migration because any particular set of levels will ultimately produce a constant age distribution if it is maintained for a sufficiently long period. If populations are aging or growing younger, the reason must be that rates of fertility, mortality, or migration are changing.

Age-specific growth rates

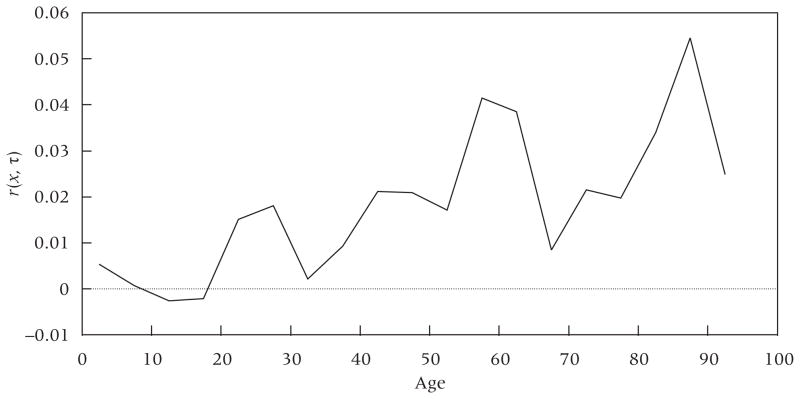
Populations grow older when, in some broad sense, growth rates are higher at older ages than at younger ages. Figure 1 shows the set of age-specific growth rates for the world’s population during the period 2005–10. It is constructed using data from the United Nations (2011). While the rates are contemporary, they reflect a century of demographic history. A line drawn through this graph would clearly be upward sloping, indicating that the world population is aging during this period. Growth rates are close to zero at ages under 20 years and rise relatively steadily thereafter, with a major peak around ages 55–65. As shown below, this disturbance has two sources, one originating in richer countries and one in poorer countries. The growth rate is relatively low at ages 90–94, reflecting a shortfall in births in more developed countries during World War I.

FIGURE 1.

Age-specific growth rates for the world, 2005–10

NOTE: Age-specific growth rates calculated for five-year age intervals. Observations located at the midpoint of each interval.

SOURCE: United Nations (2011).

A convenient and broad summary measure of aging is the rate of change in the mean age of the population. The rate of change in the mean age is equal to the covariance between age and the age-specific growth rate (Preston, Himes, and Eggers 1989). A positive covariance means that the population is growing older. The covariance for the world during 2005–10 is 0.188 years; thus, the mean age of the world population was growing older by 0.188 years per calendar year between 2005 and 2010, or from 30.49 to 31.43 years.

Demographic sources of aging

The growth rate of the population at a particular age can be traced in a simple fashion to processes of birth, death, and migration. Designate the number of persons aged x last birthday at time t as N(x, t).

$$N(x,t)=B(t-x)p(x,t-x)j(x,t-x),$$

where

• B(t − x) = Number of births in the year ending at time t − x ;

• p(x, t− x) = Proportion of birth cohort born in year ending at t− x that survived to time t;

• j(x,t − x) = Factor by which birth cohort born in year ending at t −x changed in size by time t as a result of migration.

Then the growth rate in the number of persons aged x between times t and t + 1 can be expressed as

$$\begin{array}{l}r(x,t,t+1)=ln\frac{B(t-x+1)}{B(t-x)}+ln\frac{p(x,t-x+1)}{p(x,t-x)}+ln\frac{j(x,t-x+1)}{j(x,t-x)},\\ \text{or}r(x,\tau )=r_B(x,\tau )+\mathrm{\Delta }p(x,\tau )+\mathrm{\Delta }j(x,\tau )\end{array}$$ (1)

In Equation 1, the interval t, t + 1 to which the growth rate corresponds is denoted for simplicity as τ. The three components of the growth rate at age x during the period τ are r_B(x, τ), the growth rate of births between the two cohorts born between (t−x −1 to t−x) and (t−x to t−x +1); the rate of change in the probability of surviving from birth to age x (last birthday) between the respective cohorts, Δp(x, τ); and the rate of change in migration factors between the two cohorts between birth and age x (last birthday), Δj(x, τ). Horiuchi and Preston (1988) present a continuous version of this formula and a more detailed derivation. They show that the Δp(x, τ) term is equal to (minus) the cumulative difference between birth and age x in age-specific death rates for the two adjacent cohorts, while Δj(x, τ) is the cumulative difference between the cohorts in age-specific net migration rates.

As implied by the stable population model, Equation 1 shows that it is changes in mortality and migration that add to or subtract from the inter-cohort growth rate in births. If there have been no differences in mortality or migration rates in the lifetimes of two adjacent birth cohorts up to some particular age, then mortality and migration contribute zero to the growth rate at that age.

This result may seem counterintuitive. Many people appear to believe, for example, that high immigration at young ages makes a population younger. However, the equation shows explicitly that it is changes in migration rates that contribute to the growth rate, not the level itself. This is an instance when the mind often performs the wrong experiment. The population is younger than it would be without immigration, but not younger than it was. Likewise, a population with exceptionally low mortality at very advanced ages is not necessarily having a population explosion at those ages; a mortality-induced explosion would occur only if low mortality were a recent phenomenon.

The rate of growth in the size of two successive birth cohorts, r_B(x, τ), is reflected over time in the growth rate at successively higher ages as the younger birth cohort replaces the older cohort. If there are no differences in mortality or migration rates between two adjacent cohorts, then the inter-cohort growth rate in the number of births will simply move unchanged along the age axis by one year for each calendar year that passes.

What matters for population aging is not the magnitude of the growth rate in births but age differences in that series. If births are growing at a constant rate across all ages, as in a stable population, then the birth series contributes nothing to changes in the age distribution or to population aging. Even persistently negative growth rates in births will not produce aging; only persistent declines in the growth rate of births from one period to the next could do so.

Equation 1 attributes age-specific growth rates to changes in the growth rate of births and to changes in age-specific mortality and migration rates. It provides the only framework of which we are aware that permits an identification of the sources of contemporary aging in actual populations. It is an accounting framework, analogous to the balancing equation of population growth that attributes growth rates for all ages combined to birth rates, death rates, and rates of migration. The answer supplied by this accounting approach is not necessarily the same as what would be supplied by models or by counterfactual simulations. In particular, any indirect effect of mortality change on the annual number of births is included in the r_B(x) series, rather than in the mortality series per se. Such an effect of mortality decline on births would be rejuvenating and would offset some of the aging effect resulting from inter-cohort improvements in survivorship.

Historical sources of contemporary aging

In elucidating the role of different demographic factors in aging, it is useful to distinguish between more developed (MDCs) and less developed (LDCs) countries. These groups differ significantly in both their demographic histories and their conditions of data availability. We use the UN classification system, according to which MDCs are comprised of Europe, North America, Australia, New Zealand, and Japan. Remaining countries are considered LDCs. In what follows, we have removed Eastern Europe from the set of MDCs because its demographic history is not typical of MDCs nor is that history reliably recoverable from available data.

In both groups of countries, we examine aging during the period 2005–10. Age-specific growth rates for those years are drawn from the United Nations (2011). That source also provides information on the growth rate of births during the period from 1950–55 to 2005–10. To complete the requisite demographic series, we employ different strategies for MDCs and LDCs.

Aging in more developed countries

In MDCs, reliable mortality estimates dating back to 1910 can be constructed for many countries using the Human Mortality Database (2011) and supplementary sources. We have produced life tables for the aggregate of MDCs (minus Eastern Europe) for five-year periods from 1910–14 to 2005–09. These are based upon life tables for 14 countries. The countries are grouped into three regions that are weighted in proportion to their relative size: Japan, Southern Europe, and other MDCs. Details of life table construction are presented in the Appendix. The life tables for MDCs are used to estimate the number of births in five-year periods before 1950, which is done by back-projecting the population age distribution beginning with the UN age distribution for 1950. The life tables are also used to survive birth cohorts forward—in particular, to supply the Δp(x, τ) series required for implementing Equation 1.

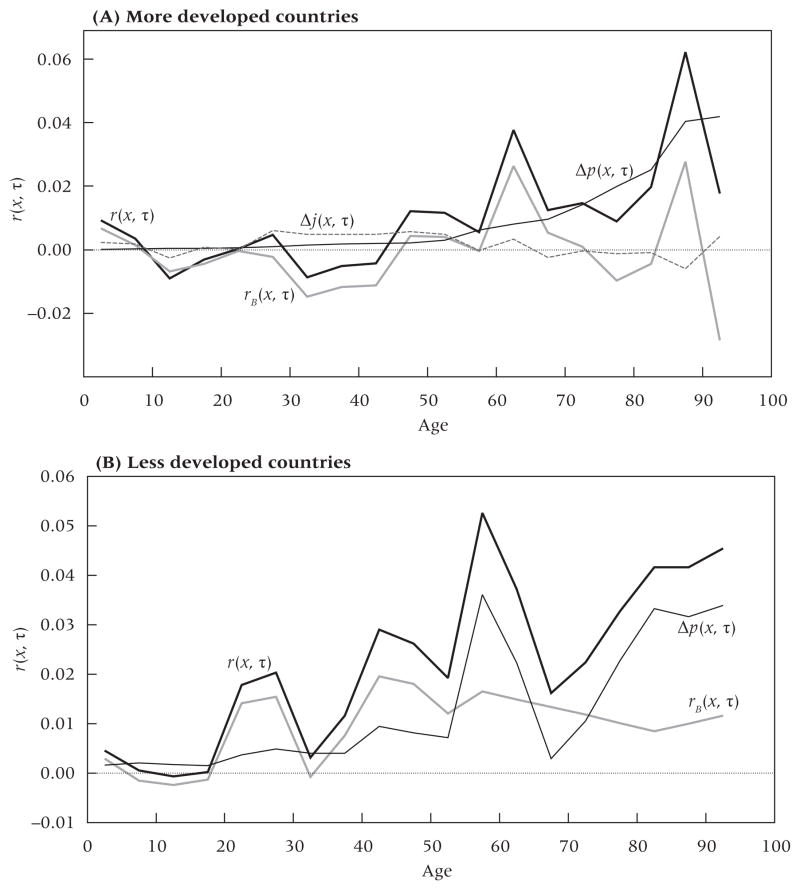
Figure 2A presents the set of age-specific growth rates for MDCs during 2005–10 as well as the estimated r_B(x), Δp(x, τ), and Δj(x, τ) series. Clearly, the set of age-specific growth rates slants upward toward higher values at older ages; as a result, the mean age of the population of MDCs rose from 39.61 in 2005 to 40.49 in 2010. The history of mortality decline has made a large contribution to aging during this period. From a value of 0.002 at ages 40–44, the Δp(x, τ) series rises steadily to a value of 0.042 at ages 90–94. In other words, the population aged 90–94 grew faster by 4.2 percent annually between 2005 and 2010 because the cohort born 1915–19 (i.e., aged 90–94 in 2010) had lower mortality up to that age than the earlier cohort born 1910–14. The mortality series increases with age because, in the cross-cohort replacements that produce age-specific growth rates, the improvements in mortality accumulate. This accumulation produced population aging by creating a high positive covariance between age and the age-specific growth rate.

FIGURE 2.

Demographic components of change in the population age structure in (A) more developed and (B) less developed countries, 2005–10

NOTE: See text for definitions of components of r(x, τ).

SOURCES: United Nations (2011); Human Mortality Database (2011). Additional data listed in the Appendix.

The birth series also contributes higher values at older ages than at younger ages. Particularly noteworthy is the fast growth of the r_B(x, τ) series in the 1945–49 period of the postwar baby boom, a growth that is now contributing to aging just as it initially contributed to population rejuvenation.

The migration series, Δj(x, τ), is derived as a residual in Equation 1. It represents movement into and out of the entire aggregate of MDCs. Figure 2A shows that changes in migration have had little effect on aging in MDCs. All values in the series are low. The values reach a sustained positive level at ages 25–55, implying that cumulative migration rates increased across birth cohorts in this range. But because these cohorts are squarely in the middle of the age distribution, the positive migration values contribute almost nothing to population aging; in fact, migration patterns have made the population slightly younger.

Because the terms on the right hand side of Equation 1 are additive, their covariances with age sum to the rate of change in the mean age of the population, 0.176 per calendar year between 2005 and 2010. Table 1 shows the covariance terms for each of the three elements for MDCs. Clearly, improvements in survivorship have contributed the largest amount to aging, 0.145 of the 0.176 change, or 82 percent. Declines in the growth rate of births contribute 0.041, or 23 percent. Changes in migration played a minor role, contributing −.010, or −6 percent to changes in mean age during this period. Thus, the massive improvements in survivorship from one birth cohort to the next during the past century are principally responsible for the aging that is occurring in more developed countries.

TABLE 1.

Sources of change in the mean age of the population, more developed (MDCs) and less developed (LDCs) countries, 2005–10

Region	Mean age			Contribution of factor to rate of change
	2005	2010	Rate of change, annualized	Inter-cohort growth rate in births	Inter-cohort cumulative change in mortality	Inter-cohort cumulative change in net migration
MDCs	39.61	40.49	0.176	0.041	0.145	−0.010
LDCs	28.46	29.51	0.209	0.102	0.107	—

SOURCES: United Nations (2011); Human Mortality Database (2011). Additional data listed in the Appendix.

Aging in less developed countries

We cannot use the same procedure for LDCs as for MDCs because far too few reliable data exist to reconstruct accurate pre-1950 mortality levels for less developed countries. Our strategy for this period relies on the assumption that the population of LDCs was stable during each decadal period from 1910–20 to 1940–50. By assuming stability, we are able to equate the growth rate of the population with the growth rate in births. We also assume that migration made no contribution to age-specific growth rates, so that the role of mortality change can be derived as a residual in equation 1. Justification for these assumptions and details of the estimation process are found in the Appendix.

The mean age of the LDC population grew by 0.209 per calendar year between 2005 and 2010, from 28.46 to 29.51 years. This increase is slightly faster than what is observed in MDCs. Figure 2B presents age-specific growth rates and their components for the period. As in MDCs, both the birth series and the mortality change series tend to rise with age, implying that both declines in the growth rate of births and gains in cohort survivorship have contributed to aging.

The Δp(x, τ) series rises relatively smoothly except for cohorts born 1945–55. Figure 2B shows a large increase in estimated survivorship for the cohort born 1945–49 relative to the cohort born 1940–44 and an even larger increase for the cohort born 1950–54 relative to that of 1945–49. The cohort born in 1940–44, on the other hand, shows little survivorship advantage relative to its immediate predecessor. The most likely source of this pattern is rapid improvements in child mortality during the late 1940s and early 1950s. In this era antimalarial programs were first deployed on a wide scale in Asia and Latin America. The main beneficiaries of these programs were young children. Antibiotics, water supply improvements, and immunization programs were allies in the effort (United Nations 1953; Reilly 2001). The age pattern of growth rates for these cohorts is not a recent phenomenon: it was already present in substantially the same form in 1950–54, as shown in the Appendix.

Our estimates in Figure 2B suggest that the birth rate series also made a small contribution to the unusually high growth rates in these cohorts, but we may have underestimated its contribution. One reason why the growth rate in births may have increased is that fetal mortality rates declined in conjunction with the implementation of health programs. In particular, maternal infection with malaria raises the risk of fetal mortality. The postwar antimalarial program in Sri Lanka appears to have reduced fetal mortality and, as a result, led to increased birth rates (Newman 1965; Lucas 2011). This phenomenon may have been widespread among countries with antimalarial programs. Below, we indicate how our estimates may be affected by this uncertainty.

Table 1 presents the rate of change in the mean age in LDCs between 2005 and 2010 and the contribution of the three demographic elements. Of the increase in mean age of 0.209 per year, improvements in cohort survivor-ship and declines in the growth rate of births are about equally responsible, contributing 0.107 and 0.102, respectively. We show in the Appendix that the relative contributions of the mortality and birth series are not sensitive to a 20 percent error in the estimated growth rate of births before 1950. To investigate the sensitivity of results to the uncertainty about the sources of rapid growth of the population aged 55–64 years, we assume that only half of the growth rate at ages 55–59 and 60–64 is attributable to mortality change, rather than the values of 68 percent and 59 percent that are reflected in Figure 2B. In this case, the proportion of the increase in the mean age attributable to mortality decline would be 45 percent, rather than the original estimate of 51 percent. The sources of aging in LDCs would still be approximately equally divided between declines in the birth series and increases in survival.

Comparing the aging processes in LDCs and MDCs, Table 1 shows that aging is occurring more rapidly in LDCs. The main reason is that the growth rate in births has declined more than twice as fast in LDCs as in MDCs. That decline is heavily concentrated in the past 40 years.

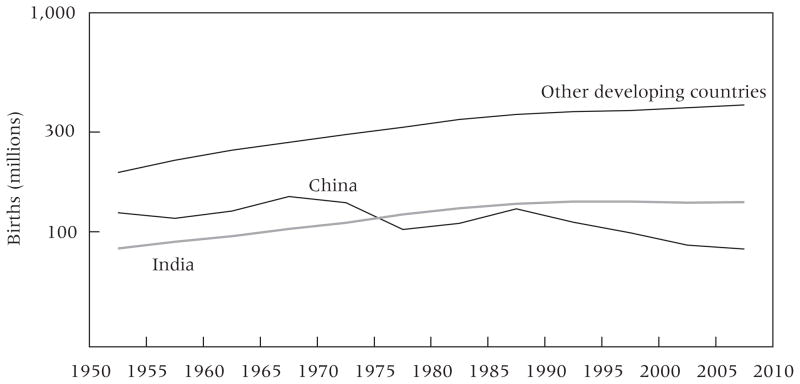
China and India together account for 45 percent of the population of LDCs in 2010, and both have contributed to the decline in the r_B(x, τ) series for LDCs. Figure 3 presents the number of births in five-year periods since 1950–55 in China, India, and the aggregate of all remaining LDCs. Because we use a log scale, the concavity evident in all three series indicates that the growth rate in the number of births has been declining. The number of births in India has clearly leveled off since 1990–95, while the number of births in China has been declining irregularly since 1965–70. Between 1970 and 1979, the largely voluntary “later, longer, fewer” policy in China, which called for later childbearing, greater spacing between children, and fewer children, reduced fertility levels. After the one-child policy was introduced in 1979, fertility levels fell more gradually (Hesketh, Lu, and Xing 2005).

FIGURE 3.

Number of births in five-year periods in China, India, and other developing countries, 1950–55 – 2005–10

SOURCE: United Nations (2011)..

Sources of change in the proportion of the population above particular ages

The mean is the most common measure of central tendency used in the social sciences. In the case of population aging, it yields simple formulas that permit decomposition of aging into its demographic sources. But in the aging world, all ages are not necessarily created equal. For example, social programs that transfer resources to older people often have an age threshold for eligibility.

To investigate how demographic factors contribute to the growth of the proportion of the population above age 65, we first express the growth rate of that proportion as

$$\begin{array}{l}\frac{\mathit{d}lnc(65+)}{dt}=r_{65+}-r_{0+}\\ =\underset{65}{\overset{\infty }{\int }}{c}^{\ast }(x)r(x)dx-\underset{0}{\overset{\infty }{\int }}c(x)r(x)dx,\end{array}$$ (2)

where c(x) dx refers to the proportion of the population aged x to x +dx, and c*(x) dx refers to the proportion of the population above age 65 that is aged x to x +dx . All functions pertain to some period τ. The expression for r(x, τ) in Equation 1 can be substituted into Equation 2. When this is done, three terms expressing differences between ages 65+ and 0+ are created, one for changes in births, another for changes in mortality, and a third for changes in migration. These three differences sum to the growth rate of the proportion of the population above age 65, thus providing an additive decomposition of the sources of growth of the proportion aged 65+. One of these difference terms, for example, represents the extent to which mortality change has increased the growth rate of the 65+ population relative to the growth rate of the population of all ages. Related approaches were used by Caselli and Vallin (1990) with reference to Italy and France and by Horiuchi (1991) with reference to Japan.

Table 2 presents the results for age groups 65+, 70+, and 75+. For the most part, the results recapitulate those achieved when the mean age of the population is used as the basic indicator of aging. In MDCs, mortality improvements are entirely responsible for the observed increase in the proportion of the population at older ages. In LDCs, both declines in mortality and a declining growth rate in the number of births contribute to the relative growth of the older population, with mortality making the larger contribution. The proportions aged 70+ and 75+ are growing faster in LDCs than in MDCs because of this additional contribution of births in LDCs. In both sets of countries, the contribution of mortality to the relative growth of the older population increases as age advances. This result clearly reflects the sharply upward-sloping mortality functions shown in Figure 2.

TABLE 2.

Sources of change in the proportion of the population above certain ages, more developed (MDCs) and less developed (LDCs) countries, 2005–10

Region	Age threshold (x)	Proportion x+		Rate of change in proportion x+, annualized	Contribution of factor to rate of change
		2005	2010		Inter-cohort growth rate in births	Inter-cohort cumulative change in mortality	Inter-cohort cumulative change in net migration
MDCs	65	0.157	0.166	0.012	0.001	0.015	−0.004
	70	0.111	0.119	0.014	−0.002	0.019	−0.003
	75	0.073	0.079	0.017	−0.004	0.024	−0.004
LDCs	65	0.055	0.058	0.012	0.004	0.007	—
	70	0.034	0.036	0.017	0.003	0.014	—
	75	0.018	0.020	0.024	0.002	0.021	—

SOURCES: United Nations (2011); Human Mortality Database (2011). Additional data listed in the Appendix.

Conclusion

The major demographic events of the past century are vividly imprinted on the series of age-specific growth rates, which together determine the rate of population aging. To investigate the demographic sources of aging, we use an accounting framework that expresses age-specific growth rates as the sum of terms representing births, survivorship, and migration. This framework reveals that, in more developed countries, the massive improvements in survivorship from one birth cohort to the next have been the most important source of aging. Less developed countries have also enjoyed huge increases in survival from one cohort to the next, with an especially rapid improvement occurring between the birth cohorts of the early 1940s and those of the early 1950s. Aging is more rapid in LDCs than in MDCs because the growth rate of births has declined faster in LDCs. China and India have made particularly large contributions to that decline. These results apply whether the measure of age structure used is the mean age or the proportion of the population above ages 65, 70, or 75 years.

Because it reflects such an extended history, the aging process has a great deal of inertia. Even if no additional improvements in survivorship were to occur, age-specific growth rate profiles will remain upward sloping for many years to come as they shift horizontally along the age axis. It would take an enormous increase in birth rates, one that history suggests is extremely unlikely, to offset the aging embedded in these profiles.

Appendix: Materials and methods

We calculated growth rates by age between 2005 and 2010 for the sexes combined using five-year age groups (0–4, 5–9…90–94) and data from the United Nations (2011). For the growth rate in the number of births, we used UN estimates of the number of births in five-year periods from 1950–55 to 2005–10. To obtain the growth rate in the number of births for earlier periods and to estimate changes in mortality and migration, we used different procedures for MDCs and LDCs.

More developed countries

For more developed countries, we estimated age-specific death rates for successive five-year periods between 1910–14 and 2005–09. We used these death rates to construct life tables for this group of countries and used the life tables to project the population by age in 1950 backward to 1910, including the number of births in a five-year period as a product of the exercise. Migration rates were assumed to be zero for purposes of the back-projection.

To estimate mortality, we extracted data on the number of deaths for both sexes combined by age and mid-year population for the period 1910 to the present from the Human Mortality Database (HMD). Data were organized into five-year age intervals with the exception of the youngest age group, which was split into 0 and 1–4. Complete or nearly complete series were available for Australia, Belgium, Denmark, England and Wales, Finland, France, Italy, Japan, the Netherlands, Norway, Spain, Sweden, and Switzerland. In the few cases where data were not available after 2007, we assumed data in the shorter interval to be representative of the full five-year period.

For Australia, data were not available on mortality in the early years for the birth cohorts of 1910–14 and 1915–19. To complete the series, we interpolated age-specific death rates from life tables for 1911 and 1921 presented in Preston, Keyfitz, and Schoen (1972).

For Japan, the HMD contained a complete series of deaths and mid-year population in five-year age and calendar-year intervals beginning in 1950. Before 1950, population data were available for 1909, 1914, 1920, 1925, 1930, 1935, 1940, and 1947 and deaths for single years between 1910 and 1943 and between 1947 and 1949. Using these data, we estimated exposure to risk in five-year intervals. For the period 1940–44, we estimated exposure using population in 1940 and 1947, and for the period 1945–49 we used population in 1947 alone. To compute the number of deaths in five-year intervals, we added deaths across single-year periods. To compute deaths for 1940–44, we assumed the number of deaths in 1944 to be the same as in 1943. To compute deaths for 1945–49, we summed deaths in 1943, 1948, and 1949 and added double the number of deaths for 1947.

For the United States, sufficient data were available from the HMD to reconstruct mortality back to 1930–34. Because HMD data began in 1933, we assumed that the mortality rate in 1933 and 1934 was representative of 1930–34. For five-year intervals between 1910–14 and 1925–29, we used period life tables by sex and single-year age in decennial years 1910–30 published by the Social Security Administration (Bell and Miller 2005). We obtained data for five-year periods by linearly interpolating death rates by age among subsequent life tables.

To obtain combined estimates for high-income countries, we separated MDCs into three groups according to subregion; we assumed these groups were representative of variation in mortality change for high-income countries as a whole. We aggregated deaths and exposure within each subregion and used these to calculate regional age-specific mortality rates for each five-year period. Next, we calculated the weighted average of the rates across subregions using relative population size of these regions in each year. For weights before 1950, we used relative population size in 1950. The first subregion was North America, Oceania, Western Europe, and Northern Europe and was represented by Australia, Belgium, Denmark, England and Wales, Finland, France, the Netherlands, Norway, Sweden, Switzerland, and the United States. The second subregion, Southern Europe, was represented by Italy and Spain; the third subregion was Japan. US estimates for 1910–14 to 1925–29 were incorporated into the first subregion by weighting age-specific mortality rates in the US by relative population size. We used these estimates for MDCs to reconstruct mortality rates by age for subsequent birth cohorts, beginning with the cohort of 1910–14. We did this by combining age-specific mortality rates for individual cohorts from each consecutive five-year period and age group. For example, the life table for the cohort born 1915–19 consisted of deaths and exposure at ages 0–4 during 1915–19, deaths and exposure at ages 5–9 during 1920–24, and so on. We estimate that life expectancy at birth improved from 51.9 years in 1920–24 to 67.2 years in 1950–54 and 80.0 years in 2005–09.

As a check on the validity of the above approach, we compared estimates of life expectancy at birth to UN values available after 1950. Our approach yielded higher values for MDCs in each year, but differences were small. The average difference across years was 0.5 and was always less than 0.8 years.

Appendix Figure 1 presents inter-cohort cumulative change in mortality between birth and attained age in 2010 for select five-year birth cohorts from 1915–19 to 1990–94 relative to the preceding birth cohort. The data underlying the plot are the combined estimates of cohort mortality by age for MDCs obtained through the above procedures. Whereas the Δp(x, τ) series that appears in Figure 2A reflects the sum of life-course differences in mortality across cohorts, Appendix Figure 1 indicates the ages at which these differences emerge. The increasing curvature beginning at approximate age 55 shows that older ages have made the largest contribution to inter-cohort mortality gains. Among earlier cohorts, however, including 1930–34, reductions in child mortality also contributed importantly to improved cumulative survival.

Less developed countries

Our strategy for the period before 1950 relies on the assumption that the population of LDCs was stable during each decadal period from 1910–20 to 1940–50. In a stable population, the growth rate in births is equal to the growth rate in population. To estimate the growth rate of the population, we rely on Livi-Bacci’s estimates of the numbers of persons in LDCs in 1900, 1920, 1930, 1940, and 1950 (Livi-Bacci 2001). These estimates are based on the author’s analysis and UN estimates. The population growth rate during period t to (t+10) was assigned to the growth rate in the number of births between (t to t+5) and (t+5 to t+10). For the rate of growth of births between periods that span two decades, we used the mean of the growth rate in the two decades. The growth rate during 1900–20 was assumed to apply to the period 1910–20; the UN growth rate for 1950–55 formed part of the final value.

These procedures produce estimates of the growth rate of births presented in Appendix Table 1. While this series provides evidence of rising growth rates during the second half of this period, it is likely that the source of the increase is declining death rates rather than rising birth rates. Declining death rates do not require the abandonment of stable assumptions; what matters is the age distribution of mortality declines.

Evidence about whether conditions of stability still pertained at the end of the period can be derived by examining age-specific growth rates during 1950–55. Appendix Figure 2 presents these rates derived from the United Nations. The growth rate series is relatively flat from ages 10–14 to 55–60, implying that “sectional stability” would be a good approximation in this range. The mean growth rate at ages 15–35 is .0163, quite close to our estimated growth rate in births of .0165 between 1945–50 and 1950–55. This consistency between growth rates in the reproductive-aged population during 1950–55 and the estimated growth rate in the number of births during 1945–55 provides some validation of the approach.

Clear evidence of destabilization is provided by the very high growth rate in the number of individuals aged 5–10 and especially aged 0–5. Because the destabilization shown in Appendix Figure 2 is essentially limited to cohorts born after 1945, the implication is that profiles of age-specific growth rates before 1945 would have been relatively flat, supporting the assumption of stability for those periods.

The second assumption used to derive estimates for LDCs is that changes in migration rates made a negligible contribution to inter-cohort changes in population size, i.e., that Δp(x, τ) is zero for LDCs. This seems a reasonable assumption because migration made a negligible contribution to population change itself. For LDCs, the UN estimates that net international migration contributed 0.000 to LDC growth rates between 1950–55 and 1985–90 and –0.001 to growth rates since then. Given its small first-order contribution, it is very unlikely that the second-order effect of changes in migration rates between cohorts is salient. More direct evidence on this point is provided by the migration estimates for MDCs presented above. These showed quite small inter-cohort changes in migration rates; of course, the principal site of origin of such migration must be LDCs (Eastern Europe is the only other possible source). With the same changes in migration flows in the numerator and a denominator that is on average 4.6 times larger in LDCs than in MDCs (the relative population size), it is clear that changes in migration must be an extremely small contributor to age-specific growth rates in LDCs. As a result, differences between age-specific growth rates and r_B(x, τ) can be confidently attributed to changes in mortality.

Because the data series for LDCs is less reliable than for MDCs, we analyzed the sensitivity of results to errors in data. The principal vulnerability is the set of r_B(x, τ) estimates before 1950. So we have repeated the covariance analysis but adding and subtracting 20 percent to the entire set of rates before 1950 (i.e., multiplying the rates by 1.20 and 0.80). The estimated contribution to aging of mortality change or change in the number of births is altered by no more than .012/year. For example, 20 percent slower growth in births before 1950 than we have estimated would raise the contribution of mortality change to changes in the mean age from .107 to .118 and lower the contribution of births from .102 to .090. Thus, results are not very sensitive to uncertainty in estimates of the growth rate in the number of births before 1950.

Decomposition of the rate of change in the mean age of the population

We first calculated the annualized rate of change in the mean age of the population for the world, MDCs, and LDCs using each region’s age distributions and a terminal age group of 90+. To calculate the contribution of changes in the number of births, mortality, and migration to the rate of change in the mean age of the population, we used the fact that the contribution of each series is equivalent to its covariance with age. Our reconstruction of the r_B(x, τ), Δp(x, τ), and Δj(x, τ), series back to 1910–14 meant that our examination of the demographic components of age-specific growth rates between 2005 and 2010 ended at ages 90–94. To ensure that all ages were represented in our series, we assumed that the proportionate distribution of components of growth for ages 90+ was the same as that for ages 90–94.

APPENDIX FIGURE 1.

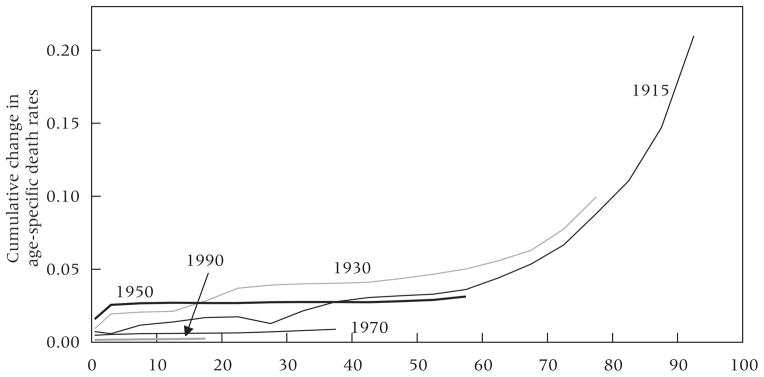
Differences in cumulative mortality between adjacent five-year birth cohorts in more developed countries

NOTE: Differences in cumulative age-specific death rates from birth to various attained ages are expressed for adjacent birth cohorts. The calendar years appearing as labels separate birth dates of two five-year-wide birth cohorts. For example, the 1915 series shows cumulative mortality for the 1910–14 birth cohort minus cumulative mortality for the 1915–19 birth cohort. More detail is available from the authors.

SOURCE: Human Mortality Database (2011).

APPENDIX FIGURE 2.

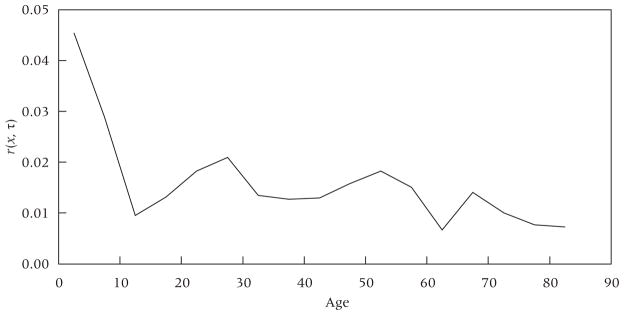
Age-specific growth rates in less developed countries, 1950–55

NOTE: Age-specific growth rates calculated for five-year age intervals. Observations located at the midpoint of each interval.

SOURCE: United Nations (2011).

APPENDIX TABLE 1.

Estimated growth rate in births in less developed countries

Period	Rate of growth
1910–15 to 1915–20	0.0116
1915–20 to 1920–25	0.0100
1920–25 to 1925–30	0.0084
1925–30 to 1930–35	0.0101
1930–35 to 1935–40	0.0118
1935–40 to 1940–45	0.0133
1940–45 to 1945–50	0.0149
1945–50 to 1950–55	0.0165

SOURCE: Livi-Bacci (2001).