Single and Multiple Ability Estimation in the SEM Framework: A Non-Informative Bayesian Estimation Approach

Abstract

Latent variable models with many categorical items and multiple latent constructs result in many dimensions of numerical integration, and the traditional frequentist estimation approach, such as maximum likelihood (ML), tends to fail due to model complexity. In such cases, Bayesian estimation with diffuse priors can be used as a viable alternative to ML estimation. The present study compares the performance of Bayesian estimation to ML estimation in estimating single or multiple ability factors across two types of measurement models in the structural equation modeling framework: a multidimensional item response theory (MIRT) model and a multiple-indicator multiple-cause (MIMIC) model. A Monte Carlo simulation study demonstrates that Bayesian estimation with diffuse priors, under various conditions, produces quite comparable results to ML estimation in the single- and multi-level MIRT and MIMIC models. Additionally, an empirical example utilizing the Multistate Bar Examination is provided to compare the practical utility of the MIRT and MIMIC models. Structural relationships among the ability factors, covariates, and a binary outcome variable are investigated through the single- and multi-level measurement models. The paper concludes with a summary of the relative advantages of Bayesian estimation over ML estimation in MIRT and MIMIC models and suggests strategies for implementing these methods.

Various topics in education or the social sciences are related to latent hypothetical constructs, such as mathematics ability, that can be examined only through observed dependent variables (i.e., indicators or test items). There have been many studies investigating ability factors and/or their relation with an outcome variable in any given test (Carlstedt, 2001; Glas & Hendrawan, 2005; Gustafsson & Balke, 1993; Kuusinen & Leskinen, 1988; Undheim & Gustafsson, 1987). These studies estimated or tested ability factors either in the structural equation modeling (SEM) or in the item response theory (IRT) frameworks. Both SEM and IRT can be used for factor analysis of dichotomous item responses, in which the measurement model in the SEM approach is formally equivalent to an IRT model (Clockner-Rist & Hoijink, 2003). Some of the ability studies examined a single ability factor (general ability), while others examined multiple ability factors (specific abilities) as well as a single ability factor. For example, Gustafsson and Balke (1993) investigated the relations between aptitude variables and school achievement scores using some factor models, a higher-order factor model and a bi-factor model, that allowed simultaneous identification of general and specific abilities.

Two types of measurement models in the SEM framework are considered in estimating multiple (specific) ability factors and a single (general) ability factor in the present study: one is an IRT model, and the other is a multiple-indicator multiple-cause (MIMIC; Jöreskog & Goldberger, 1975) model. IRT models traditionally use a continuous factor score variable (latent variable) as an ability factor, and these models are based on the idea that the probability of answering an item correctly (i.e., the performance of an individual item) is a function of that ability. In the present study, a multidimensional IRT (MIRT) model is considered for accommodating the case of multiple ability factor estimation and ascertaining how individual items perform with respect to those multiple ability factors. There is a simpler alternative model in which subtest (or subsequent dimension) scores are used as continuous indicator variables instead of using the individual item scores (i.e., categorical variables). It is a factor analytic model with incorporated covariates, also termed a MIMIC model. A MIMIC model can save a substantial amount of estimation time compared to an MIRT model. Numerical integration is needed to estimate an MIRT model using maximum likelihood (ML) estimation; it becomes increasingly computationally demanding as the number of factors, the number of items, and/or the sample size increase (Muthén & Muthén, 2010). However, the MIRT approach allows us to estimate multiple, specific ability parameters, whereas the MIMIC (or a factor) approach is not able to estimate them because specific sub-dimension scores are used as indicator variables.

The primary purpose of the present study is to compare the performance of Bayesian estimation to ML estimation methods in estimating specific or general ability factors using the MIRT and MIMIC models. The main objective of this study is accomplished through a series of Monte Carlo (MC) simulations within the SEM framework. In addition, the usefulness of the MIRT model, despite its complexity, compared to the MIMIC model is discussed through a real data analysis utilizing multistate bar examination (MBE) data. The structural relationships among an ability factor(s), covariates (e.g., undergraduate grade point average and law school admission test), and proximal/distal outcomes (e.g., pass or fail) are examined across the two types of measurement models. If the structural relationships are similar enough between the two models and if one is interested only in those relationships, the simpler MIMIC model can be a practical alternative to the more complex MIRT model.

In the present study, an important motivating data example was the MBE data. The MBE is a six-hour, 200-question multiple-choice examination covering six subtest areas (constitutional law [CNL], contracts [CTR], criminal law and procedure [CRM], evidence [EVD], real property [RLP], and torts [TOR]), which was developed by the National Conference of Bar Examiners (NCBE). We first tried to fit the MIRT and MIMIC models to the complex, six-dimensional MBE data using ML estimation to compare structural relationships between the two models. However, the estimation of the MIRT models with the MBE data consumed a tremendous amount of computation time without success, probably because of multiple continuous latent variables (six ability factors) with many categorical observed variables. It has been generally known that many models are computationally cumbersome or impossible using ML, such as with categorical outcomes and many latent variables resulting in many dimensions of numerical integration (Muthén & Asparouhov, 2010). On the other hand, Bayesian estimation with diffuse (non-informative) priors provided plausible results in the MBE data analysis within a reasonable timeframe.¹

The Bayesian estimation approach was used in this motivating example as an alternative to ML estimation because initial runs using the ML estimation approach failed to converge to a satisfactory solution even after a month of continuous computation.² Since the Bayesian estimation approach was a matter of practical convenience, proper verification was needed as to whether the ML and Bayesian estimation results in the SEM framework were comparable for both the MIRT and MIMIC models. The ML estimation time with MIMIC models was almost instant, enabling direct comparison of parameter estimates derived from the ML and the Bayesian methods. Non-convergence, however, was a major problem with the MIRT models. To address this problem, comprehensive Monte Carlo simulations were conducted to compare the ML and Bayesian estimation approaches with MIRT models. Considering the importance of MIMIC models in this study,³ a simulation study with MIMIC models was also performed. The simulations had multilevel extensions of the MIRT and MIMIC models to emulate the nesting within jurisdictions that exists with the motivating MBE data example. The multilevel structure was also applied to the real data analysis of the MBE data. The real data analysis and the simulation study provide a general idea of whether the structural relationships are comparable between the MIRT and MIMIC models and whether Bayesian estimation of MIRT and MIMIC models in the SEM framework can be a reasonable alternative to ML estimation. All of the analyses and simulations in this study were carried out using Mplus 6 (Muthén & Muthén, 2010) on a personal computer under Windows 7.

The organization of this study is as follows. The following two sections contain overviews of the IRT and MIMIC models and the Bayesian estimation method for the purpose of the real data analysis and the Monte Carlo simulation study. Next, a section presents real data analyses using the motivating MBE data and details the results. The next section addresses the method, presenting the procedures for the design and data analysis for the Monte Carlo study, and provides simulation results. The MBE data example is presented prior to the main Monte Carlo study because (1) the Monte Carlo study was motivated by the confronting estimation problem using ML, and (2) MC simulation conditions were generated while reflecting the MBE testing circumstances. Discussion and conclusions are presented in the final section.

Models

Item Response Theory Models

IRT models represent the relationship between the latent trait (θ; ability) and the performance on a set of categorically scored items (i.e., the probability of a correct response). Dichotomous IRT models are described by the number of item parameters they make use of. A two-parameter logistic (2PL) model, which was used in this study, is briefly:

$$P\left(U_{ij}=1\mid {\theta }_j\right)=\frac{\mathit{exp}\left[a_i\left({\theta }_j-b_i\right)\right]}{1+\mathit{exp}\left[a_i\left({\theta }_j-b_i\right)\right]},$$ (1)

where a_i represents the discrimination of the item i, b_i represents the difficulty of the item i, θ_j is a latent trait or ability level of a person j, and P(U_ij = 1|θ_j) is the probability of endorsing the item i given a person j’s ability level. When the 2PL model is estimated in the SEM framework, the relationships between the a and b parameters of IRT and the Mplus parameters are as follows:

$$a=\lambda ,b=\frac{\mathit{threshold}}{\lambda },$$ (2)

where λ is a factor loading, and threshold is a kind of intercept in the logistic link function.⁴

Standard IRT models involve one-factor (one-ability) models, also called unidimensional IRT models. With educational testing in particular, these models have proven very effective, such as with the scholastic aptitude test (SAT), the graduate record examination (GRE), and the law school admission test (LSAT) (Uebersax, 1993). However, solving complex ability test items typically involves a series of mental operations (components or dimensions), each of which can be considered as a separate cognitive construct (Whitely, 1980). Furthermore, some tests have designs that lead one to expect natural multidimensionality, such as the MBE with six subtest areas.

A multidimensional 2PL model can be expressed as:

$$P(U_{ij}=1\mid {\mathit{\theta }}_{\mathit{j}})=\frac{\mathit{exp}\left[{\mathit{a}}_{\mathit{i}}{\mathit{\theta }}_{\mathit{j}}+d_i\right]}{1+\mathit{exp}\left[{\mathit{a}}_{\mathit{i}}{\mathit{\theta }}_{\mathit{j}}+d_i\right]},$$ (3)

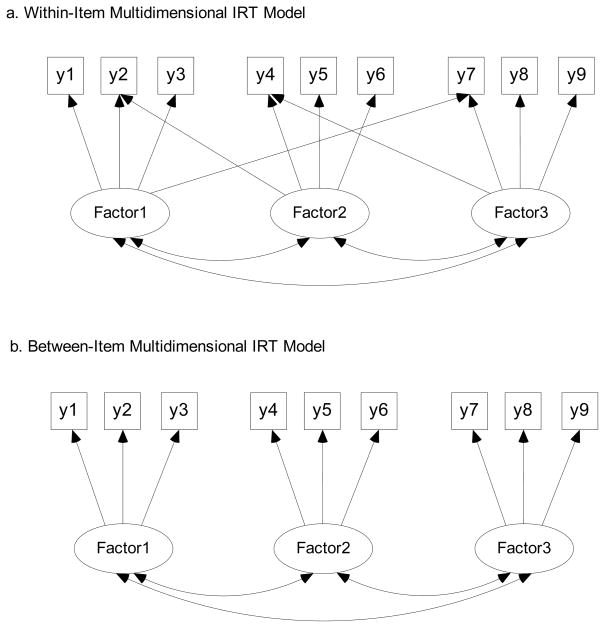
where θ_j represents multiple ability parameters associated with each respondent, a_i represents multiple discrimination parameters associated with each item, and d_i represents an item’s location on an item response surface. Path diagrams for two types of MIRT models (within- and between-item MIRT models) are provided in Figure 1. In general, the within-item model is more appropriate for analyzing a test with each item measuring two or more intentionally defined abilities, while the between-item model is more suitable for analyzing a test that measures several subsets of domains (Oshima, Raju, & Flowers, 1997; Wang, Wilson, & Adams, 1995). Although cross-loadings are possible among multiple latent abilities and individual items (Figure 1a), the between-item MIRT model (Figure 1b) is more relevant to our motivating example because the MBE consists of six subtest areas implying a simple structure of relationships between the multiple abilities and individual items.

Figure 1.

Two types of multidimensional IRT models.

Multidimensional models are best (1) when there is an assumed multidimensional structure to the set of items, and one wishes to understand the multidimensional structure and (2) when there are a large number of items, say 50 or more (Uebersax, 1993). In the present study, we acknowledge the multidimensionality by directly applying between-item MIRT models in the six subtest structures of the MBE and in the multiple generated factors through an MC study.

Multiple-Indicator Multiple-Cause (MIMIC) Model

A MIMIC model (Jöreskog & Goldberger, 1975) is a special case of the more general structural equation model that contains one or more latent variables that are simultaneously identified by both multiple endogenous indicator variables (i.e., items) and by single or multiple exogenous causal variables (i.e., covariates). The MIMIC model is used to study (1) the effects of covariates on factors and (2) the effects of covariates on observed outcome variables (i.e., indicator variables). The former is related to testing population heterogeneity, which is the relationship between the covariates and the factors. If they are significant, this indicates that the factor means are different for different levels of the covariates. The latter is associated with testing measurement non-invariance, and it is called differential item functioning (DIF) analysis in the context of IRT; if interested, see Muthén (1989) or Woods (2009).

A MIMIC model is composed of two modeling parts: the measurement model

$$\mathit{y}={\mathit{\Lambda }}_{\mathit{y}}\mathit{\eta }+\mathit{\epsilon },$$ (4)

and the structural model

$$\mathit{\eta }=\mathit{\Gamma }\mathit{x}+\mathit{\zeta },$$ (5)

where y represents a vector of indicator variables (observed outcome variables), Λ_y is the loading matrix for the factor model, η represents a vector of factors, ε represents a vector of measurement errors, Γ is the regression coefficient matrix, x represents a vector of covariates for latent variables, and ζ is the disturbance vector. A MIMIC model is able to test the factor structure of a measure as in traditional confirmatory factor analysis (CFA) while simultaneously testing the effects of observed exogenous variables (x) on the latent factors (η).

Incorporation of Covariates and Outcome Variables

There are several advantages of placing a model in an SEM or latent variable context. One of them includes the ease with which one can incorporate covariates or outcome variables and estimate the effects of those variables in a single estimation process. Covariates can be easily added to a CFA model so that a MIMIC model is formulated. Covariates can also be easily added to an IRT model because an IRT model can be regarded as a CFA model with a different parameterization when analyzed from an SEM perspective (see e.g., Kamata & Bauer, 2008; McDonald, 1999; Takane & de Leeuw, 1987). Incorporating a binary outcome variable (e.g., 1 = ‘pass’ or 0 = ‘fail’) into an IRT or a MIMIC model is also allowed in the SEM framework, resulting in logistic regressions with the outcome variable being a dependent variable and the factors or the covariates being independent variables.

Bayesian Estimation

If one has a model that is computationally demanding and/or conventional frequentist approaches (i.e., ML estimation) fail to converge, Bayesian estimation is not a fancy option but an important and realistic alternative to ML estimation. Such an analyst may view the Bayesian analysis simply as a computational tool for getting estimates that are analogous to what would have been obtained by ML estimation had it been feasible (Muthén & Asparouhov, 2010). This is usually conducted with diffuse (non-informative) priors. In this section, Bayesian statistical inference is briefly reviewed for the purpose of the simulation study and the real data analysis (for details, see e.g., Hoff, 2009; Kaplan & Depaoli, 2012; Muthén & Asparouhov, 2010).

In statistical inference, the goal is to obtain estimates of the unknown parameters (θ) given data (y). The main difference between frequentist statistical inference, ML estimation, and Bayesian statistical inference is the nature of the unknown parameters, θ. In the ML estimation, the assumption is that θ are unknown, but fixed, whereas in Bayesian estimation, θ are random, possessing a probability distribution which reflects our uncertainty about the true value of θ (i.e., posterior distribution). More formally,

$$p(\theta \mid y)=\frac{p(\theta ,y)}{p(y)}=\frac{p(y\mid \theta )p(\theta )}{p(y)},$$ (6)

where p(θ|y) is referred to as the posterior distribution of the parameters θ given the observed data y, p(θ, y) is the joint probability of θ and y, p(y) is the probability of observing y, p(y|θ) is the probability of observing y given unknown parameters θ, and p(θ) is the prior distribution of the parameters. This equation is Bayes’ Theorem.

One distinguishing feature of Bayesian estimation is the specification of prior distributions for the model parameters. Priors can be non-informative or informative based on how much information we believe we have prior to the data collection and how accurate we believe that information to be. A non-informative prior (also known as a diffuse prior), which was used in this study, has a large variance reflecting large uncertainty in the parameter value. With a large prior variance, the likelihood contributes relatively more information to the formation of the posterior and the estimate is closer to a maximum likelihood estimate.

With a posterior distribution in hand, summarizing the distribution provides the necessary elements for Bayesian hypothesis testing. The mean of the posterior distribution can be written as

$${\widehat{\theta }}_{\mathit{EAP}}(y)={\int }_{-\infty }^{\infty }\theta p(\theta \mid y)d\theta ,$$ (7)

and is referred to as the expected a posteriori (EAP) estimate. Similarly, the conditional variance of θ (Gill, 2002) can be obtained as

$$\mathit{Var}(\theta \mid y)=E[{(\theta -E[\theta \mid y])}^2\mid y]=E({\theta }^2\mid y)-E{(\theta \mid y)}^2.$$ (8)

The Bayesian perspective also forms a credibility interval, just like the confidence interval in the frequentist statistical inference. Formally, a 100(1 − α)% credibility interval for a particular subset (C) of the parameter space θ is defined as

$$1-\alpha ={\int }_{c}p(\theta \mid y)d\theta .$$ (9)

As opposed to the interpretation of a confidence interval, a 100(1 − α)% credibility interval means that the probability that the parameter lies in the interval is 1 − α.⁵

For the simulation study and the real data analysis, convergence is determined using the Gelman-Rubin convergence diagnostic (Gelman & Rubin, 1992; Gelman, Carlin, Stern, & Rubin, 2004). This considers the potential scale reduction (PSR) factor. The comparison of between and within variances is utilized, and large values typically indicate that the chain in the Markov chain Monte Carlo (MCMC) sampling method has not fully explored the target distribution. In this study, 1.1 of PSR (Gelman et al., 2004) is used as a convergence criterion for all parameters. For the model comparison, deviance information criterion (DIC) was developed by Spiegelhalter, Best, Carlin, and Linde (2002). This index can be used just as the AIC (Akaike, 1974) or the BIC (Schwarz, 1978)--the lower, the better.

Real Data Analyses

Data

For the real data example, 2,983 examinees were randomly drawn from the July 2010 administration of the MBE who had provided consent. Data included 41 states with 36 – 91 candidates in each state and complete (i.e., no missing) data on all measures. Of the 200 items on the MBE, 174 (30 CNL, 31 CTR, 27 CRM, 29 EVD, 28 RLP, and 28 TOR) were used in this study. Some items were excluded for several critical reasons including multi keys, breaches, poor statistical characteristics, changes to the law, etc. Undergraduate grade point average (UGPA; M = 3.35, SD = .424) and law school admission test (LSAT; M = 155.74, SD = 6.952) scores were used as covariates. A binary variable indicating pass/fail (pass = 79.7% and fail = 20.3%) was formulated as an outcome variable in the models. In fact, each jurisdiction sets its own passing standard and has its own bar exam,⁶ so there is no single, apparent threshold indicating pass or fail. However, the minimum passing standards (MPS) ranged from 128 to 145, and the median and modal MPS was 135 based upon the information of previous 2008 data from 41 jurisdictions. For purposes of the study, a score of 135 or above on the MBE scale was chosen as a passing standard, and a pass/fail variable was created (1 = ‘pass’ or 0 = ‘fail’).

Multidimensional IRT Models

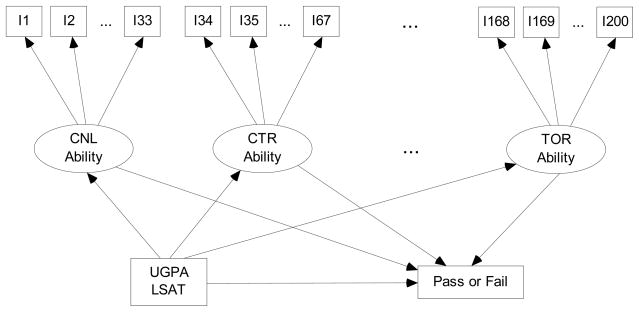
In this section, the results of six-dimensional IRT models (both single- and multilevel) are provided. For the single-level MIRT model, six ability factors were estimated from the six subtest dimensions of the MBE. Two covariates, UGPA and LSAT, and the outcome variable, pass/fail, were added to the models. Regression paths between the covariates, the outcome, and the ability factors were specified as in Figure 2. The model was estimated via Bayesian approach with default diffuse priors in Mplus, which are provided in the Appendix.

Figure 2.

A multidimensional IRT model using the MBE item-level data.

Estimates based on the post burn-in iterations⁷ for the single-level MIRT model are presented in the left columns of Table 1. Only structural relationship parameter estimates (e.g., regression paths) are provided since those were of interest in this study as well as there were too many factor loading and threshold parameters (i.e., 174 a and b parameters in an IRT framework) to be shown. The EAP estimates and standard deviations of the posterior distributions are presented for each parameter. The one-tailed p-value based on the posterior distribution is also included for each parameter. If the parameter estimate is positive, this p-value represents the proportion of the posterior distribution that is below zero. If the parameter estimate is negative, the p-value is the proportion of the posterior distribution that is above zero (Muthén, 2010). A 99% credibility interval for each parameter is also provided.

Table 1.

Bayesian Estimation Results of MIRT Models

	Single-level MIRT			Multilevel MIRT
	EAP (SD)	p	99% CI	EAP (SD)	p	99% CI
Constitutional Law on
UGPA	0.601 (.062)	.000	0.442, 0.763	0.596 (.063)	.000	0.433, 0.759
LSAT	0.035 (.004)	.000	0.025, 0.046	0.033 (.004)	.000	0.022, 0.042
Contracts on
UGPA	0.487 (.056)	.000	0.343, 0.632	0.478 (.057)	.000	0.331, 0.624
LSAT	0.026 (.003)	.000	0.018, 0.034	0.023 (.003)	.000	0.013, 0.029
Criminal Law and Procedure on
UGPA	0.439 (.067)	.000	0.265, 0.610	0.425 (.067)	.000	0.254, 0.598
LSAT	0.041 (.004)	.000	0.030, 0.051	0.038 (.004)	.000	0.028, 0.046
Evidence on
UGPA	0.510 (.058)	.000	0.359, 0.658	0.503 (.059)	.000	0.350, 0.655
LSAT	0.035 (.003)	.000	0.026, 0.043	0.032 (.004)	.000	0.020, 0.040
Real Property on
UGPA	0.471 (.057)	.000	0.323, 0.617	0.458 (.058)	.000	0.311, 0.608
LSAT	0.042 (.004)	.000	0.033, 0.052	0.037 (.004)	.000	0.025, 0.047
Torts on
UGPA	0.415 (.062)	.000	0.257, 0.577	0.415 (.064)	.000	0.249, 0.581
LSAT	0.024 (.003)	.000	0.016, 0.032	0.022 (.005)	.000	0.009, 0.033
‘Pass or Fail’ on
Constitutional Law	0.869 (.315)	.002	0.060, 1.760	0.995 (.402)	.004	−0.042, 2.211
Contracts	1.173 (.418)	.002	0.145, 2.381	1.359 (.520)	.002	0.103, 2.991
Criminal Law and Procedure	0.847 (.360)	.007	−0.072, 1.849	1.002 (.432)	.005	−0.063, 2.299
Evidence	1.130 (.343)	.000	0.284, 2.101	1.305 (.424)	.000	0.352, 2.611
Real Property	0.816 (.394)	.017	−0.200, 1.927	0.950 (.460)	.017	−0.282, 2.305
Torts	1.099 (.385)	.002	0.136, 2.205	1.279 (.493)	.002	0.093, 2.730
‘Pass or Fail’ on
UGPA	−0.599 (.259)	.007	−1.316, 0.036	−0.695 (.303)	.004	−1.572, 0.020
LSAT	−0.104 (.025)	.000	−0.178, −0.046	−0.116 (.026)	.000	−0.180, −0.059

Note. EAP represents expected a posteriori, which is a point estimate. SD represents standard deviation. p represents one-tailed p-value. 99% CI represents 99% credibility interval.

There are several findings to be reported. First, given the parameter estimates in Table 1, all of the regressions of the six ability factors on UGPA and LSAT were positively significant at p < .01 level,⁸ meaning the scores of the six ability factors increased as the UGPA and LSAT increased at a rate that would happen by chance less than 1% of the time. Second, all of the logistic regressions of the outcome variable on the six ability factors were positively significant at p < .01, except for the factor related to real property (RLP) (one-tailed p = .017). That is, the probability of passing the exam significantly increased as each of the ability factor scores increased, except for the RLP ability factor. Third, the logistic regressions between the outcome variable and the covariates were negatively significant. This should not be interpreted as if the probability of passing the exam decreased as the UGPA and LSAT increased, because the ability factors were functioning as mediators in the model. In fact, when separately modeled in a path analysis, the UGPA and LSAT were significant positive predictors (γ_UGPA = .485, p < .001, and γ_LSAT = .069, p < .001) of the outcome variable. It appears that the six ability factors mediated the relationship between the covariates and the outcome variable. By adding the mediators (i.e., six ability factors), the relationship between the covariates and the outcome variable became even negative because the relationships between the mediators and the covariates and between the mediators and the outcome variables were highly positively significant. Lastly, the six ability factors were all highly correlated and statistically significant, with the correlations ranging from .799 to .904.

The application of MIRT modeling in the SEM framework should also take nested effects into account since the MBE data being modeled arose from multistage sampling. Ignoring the between-state variability would result in predictable biases in the parameters of the MIRT model when there was significant between-state variation. Therefore, it was desirable to apply multilevel methodology to the MIRT model, and the results are provided in the right columns of Table 1. In the multilevel MIRT model, the within part of the model stayed the same as the single-level MIRT model, and the between part of the model was basically null without any random effects for within-level coefficients.⁹ As such, there were no structural relationship parameters in the between part of the model, and consequently only the results of the within part of the model are provided in the table. In other words, in the multilevel MIRT, individual level parameters were estimated taking the multilevel structure into account. Overall, standard deviations as well as point estimates were quite similar, but the standard deviations of the regression coefficients were a bit higher than those of the single-level model. The corresponding p-values were also similar. From the results, we may reasonably guess that there was very minimal intraclass correlation (i.e., small between-state variation) in the items, meaning there was not a large difference in response patterns on the MBE across 41 states.

Convergence plots, posterior density plots, and auto-correlation plots (for all chains in MCMC) for all parameters were provided through Bayesian estimation in Mplus, but they are not reported here to save space. Note also that model comparison indices were not available for these particular data examples and are thus not presented here. This is an area within MCMC estimation that requires further research (Kaplan & Depaoli, 2012).

MIMIC Models

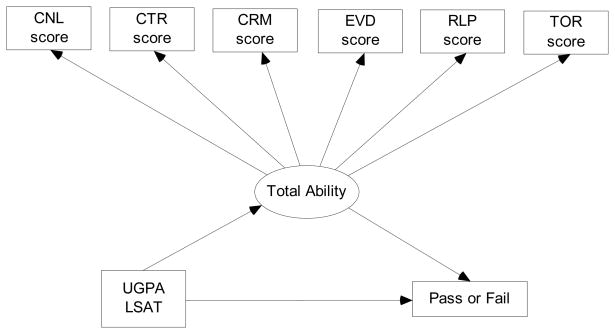
Instead of using all 174 binary items, six subtest scores, in this section, were used as indicator variables for a CFA model that had only one ability factor (general or total ability factor). Adding the UGPA and LSAT to the CFA model yielded a MIMIC model, and the outcome on the MBE was incorporated to the MIMIC model. A path diagram for this model is displayed in Figure 3. The model was also estimated via Bayesian approach with default diffuse priors in Mplus, which are specified in the Appendix.

Figure 3.

A MIMIC model using the MBE subtest-level data.

The results of the single-level MIMIC model are provided in the left columns of Table 2. Only structural relationship parameter estimates are provided as in the MIRT results. There are several findings worth highlighting. First, the regression coefficients of the total ability factor on the covariates were positively significant, meaning that UGPA and LSAT were positively related to the general ability on the MBE. Second, the logistic regression coefficient of the outcome variable on the total ability factor was also positively significant, meaning that the general ability measured by the six subtest scores was positively related to the pass/fail indicator on the MBE. Lastly, the logistic regression coefficients of the outcome variable on the covariates were negative; the UGPA was not significant (p = .014), while the LSAT was significant (p < .001). These results are similar to those obtained with MIRT and would have the same interpretation. That is, the relationship between the covariates and the outcome variable was fully mediated by the total ability factor.

Table 2.

Bayesian Estimation Results of MIMIC Models

	Single-level MIMIC			Multilevel MIMIC
	EAP (SD)	p	99% CI	EAP (SD)	p	99% CI
Total (general) ability on
UGPA	0.517 (.060)	.000	0.367, 0.670	0.593 (.054)	.000	0.450, 0.729
LSAT	0.042 (.012)	.000	0.020, 0.061	0.067 (.009)	.000	0.048, 0.080
‘Pass or Fail’ on
Total (general) ability	4.756 (1.126)	.000	3.333, 7.599	4.120 (.240)	.000	3.559, 4.749
‘Pass or Fail’ on
UGPA	−0.494 (.257)	.014	−1.204, 0.134	−0.450 (.222)	.021	−1.051, 0.110
LSAT	−0.086 (.023)	.000	−0.154, −0.042	−0.061 (.017)	.000	−0.108, −0.108

Note. EAP represents expected a posteriori, which is a point estimate. SD represents standard deviation. p represents one-tailed p-value. 99% CI represents 99% credibility interval.

The multilevel extension was also applied to the MIMIC model. The within part of the model stayed the same as the single-level MIMIC model, one factor model with the covariates and the outcome variable. In the between part of the model, we specified a one-factor model without between-level covariates or outcome variables. For the comparison, the within part results are provided in the right columns of Table 2. Overall, the estimates and their significance were close to the results of the single-level MIMIC model. The intraclass correlations of the six indicator variables (CNL, CTR, CRM, EVD, RLP, and TOR subtest scores) ranged from .014 to .025, indicating little between-state variability in the data.¹⁰ These intraclass correlations correspond to the fact that the single-level estimates and the multilevel estimates were quite comparable.

Comparison of the Two Models

The results were quite similar in terms of the structural relationships among the ability factors, the covariates, and the outcome variable, which implies that MIMIC models may be used to study structural relationships as an alternative to the computationally demanding MIRT models. However, the more complicated MIRT models provided some advantages over the simpler MIMIC models. First, we found that some items were not significantly related to their specified dimensions (specific ability factors) in the MIRT model. For example, three items did not measure their corresponding ability factors (i.e., three items did not discriminate examinees’ abilities) significantly under 1% of α: CNL 7 (p = .017), CRM 18 (p = .472), and EVD 24 (p = .141). Item fit could not be tested in the MIMIC models, because the MIMIC models used only the subarea scores for the analysis. Second, we found that the RLP ability factor estimated in the MIRT model did not significantly predict the outcome variable under 1% of α (p = .017), meaning the ability factor measured by real property items was not a good predictor of the outcome, pass or fail, controlling for the other five ability factors. In the MIMIC models, it was not possible to examine the relationship between a specific ability factor and the outcome variable because the MIMIC models do not have a specific ability factor. In sum, although the MIRT models had the more complicated specification and required much longer estimation time even with Bayesian approach, those models were quite useful in the sense that they provided item-level and subtest-level information, which were not provided by the MIMIC models.

A Monte Carlo Study

In this section, Monte Carlo simulations were carried out for investigations and comparisons of the performances of two statistical estimators, maximum likelihood estimation with robust standard errors and Bayesian estimation with diffuse priors. The study examined parameter recovery of the two estimators and the degree to which the two estimators were comparable.

Study Design and Data Generation

For conducting the simulation study, the MIRT model and the MIMIC model were chosen to specify Monte Carlo variables and population specifications. As the Monte Carlo variables, sample sizes of 500, 1,000 and 3,000 were considered for the two models, and 100 replications were generated in each condition. Then, population variables for both the MIRT and the MIMIC simulations were determined: (1) levels for the model, (2) number of factors, (3) number of items, and (4) number of covariates.

For the MIRT model, specifically, the first population factor to consider was the number of levels for the model: single-level and multilevel. Since Bayesian estimation was applied to both single- and multi-level models in the previous examples, these two conditions were reasonable. To emulate a nested data structure, 50 groups were generated with 8 to 12 individuals in each group for a sample size of 500, with 16 to 24 individuals for a sample size of 1,000, and with 40 to 80 individuals for a sample size of 3,000. The second factor was the number of latent variables: 2 and 3 factors. The choice of six latent variables across all conditions would have been ideal, but this would result in the same convergence problem encountered with the actual data, particularly for ML. The third factor was the number of binary items per each factor: 3 and 6 items. The last factor was the number of covariates: 0 and 1. IRT models are frequently used without covariates, but, in this study, covariates were added to the models. Therefore, the models with and without a covariate were considered. The MIRT models investigated were generated on the basis of the sample size and the four crossed design factors for the purposes of the simulation study (a total of 48 conditions). For the all of the generated conditions, one binary outcome variable (fail coded 0 and pass coded 1) were incorporated. Factor loadings for each item ranged from 0.5 to 1.6, and threshold values of each item ranged from −1.0 to 1.5 arbitrarily, which were, in the authors’ experience, quite common numbers in IRT models in the SEM framework. Across all the conditions, there were no missing responses.

For the MIMIC model, the first population factor to consider was the same as in the MIRT simulations. The second factor was the number of latent variables: 1 and 2 factors. The third factor was the number of continuous indicators per each factor: 3 and 6 items. For simplicity, the means and the standard deviations of all the items were set to be 0 and 0.5, respectively. The last factor was the number of covariates: 1 and 2 covariates. The MIMIC models investigated were also generated on the basis of the sample size and the four crossed design factors for the purposes of the simulation study (a total of 48 conditions). As before, one binary outcome variable was incorporated, and there were no missing responses.

In addition to the planned simulations for the MIRT and MMIC models above, the simulations were expanded to deal with MIRT models under very high complexity. Although the simulations of the MIRT models with a limited number of factors and items (e.g., 3 factors and 6 items each) might give us a good sense overall about the relative performance of Bayesian estimation to ML, their complexity did not match with our motivating MBE data example. For this reason, we considered some select conditions that were as complex as the MBE data: 3 factors with 30 and 60 dichotomous items, and 6 factors with 15 and 30 dichotomous items across the three sample sizes, 500, 1,000, and 3,000. Since, as expected, ML showed very lengthy estimation time under these high complex conditions (e.g., several days per single replication), we performed only Bayesian estimation with the generated data sets. In addition, when the sample size was small (i.e., N = 500) Bayesian estimation under multilevel settings frequently showed non-convergence within the maximum specified number of iterations, which was 100,000. Multilevel MIRT models under the highest complexity (e.g., 3 factors and 60 items each, and 6 factors and 30 items each) also took tremendous amount of estimation time regardless of the sample size. Therefore, these expanded simulations were carried out under some limited modeling settings.

Data Analysis Strategy

Data sets were generated according to the simulation factor conditions, and the MIRT and MIMIC models were estimated using the two estimators. The discrepancies (1) between population parameters and averaged ML estimates over replications and (2) between population parameters and averaged Bayesian estimates over replications were examined across all the generated conditions using averaged absolute biases (AAB) and root mean square errors (RMSE). The AABs were calculated using absolute values in this study to assess models’ overall discrepancy between parameters and estimates:

$$\mathit{AAB}=\frac{{\sum }_{k=1}^p\mid {\overline{\theta }}_k-{\theta }_k\mid }{p},$$ (10)

where p is the number of free parameters, θ_k is the parameter value, and θ̄_k is the averaged parameter estimate across replications. The AAB of the present study is differentiated from the commonly used mean bias (MB) in that an MB is calculated for an estimate over replications while an AAB is calculated over averaged estimates for a model. The RMSEs were calculated as:

$$\mathit{RMSE}=\sqrt{\frac{{\sum }_{k=1}^p{({\overline{\theta }}_k-{\theta }_k)}^2}{p}}.$$ (11)

The calculation of RMSE differs by situation. In a Monte Carlo simulation study, the RMSE is calculated over replications to assess the variability of each estimate. In this study, it was calculated over multiple parameters using averaged estimates over replications to assess the precision of a model.

Both the AAB and RMSE are designed to be close to zero if averaged estimates are close to parameter values. Here, the AAB and RMSE may not be used as an absolute indicator of determining whether an estimator is legitimate or not, because there is no commonly accepted threshold to decide on whether an estimator is valid or not. Therefore, these two indices were used together to compare the relative performance of the ML and Bayesian estimation methods.

Simulation Results

The AABs and RMSEs between ML estimation with robust standard errors and Bayesian estimation with diffuse priors for MIRT models are compared in Tables 3 and 4. Although there was no large performance difference between the estimators, some noticeable patterns were observed. First, the performances of both ML and Bayesian estimators were, overall, slightly better with more binary items and with an added covariate, while the influence of the number of factors was trivial. Second, the performances of the estimators became substantially better as sample sizes increased from 500 to 3,000. The AAB and RMSE improvement due to the larger sample size was more obvious with Bayesian estimation than with ML estimation. Third, the performances of the estimators were somewhat different across the single- and multi-level modeling settings. ML estimation was overall better than Bayesian estimation across the single- and multi-level models, whereas Bayesian estimation was better than ML estimation in the multi-level models with sample sizes of 3,000. Lastly, the patterns of the AAB and RMSE were similar, meaning that when the AAB increased, the RMSE also increased, and vice versa.

Table 3.

ML and Bayesian Estimation Performances for Single-Level MIRT Models

					Parameters vs. ML estimates		Parameters vs. Bayesian estimates
Factors	Items	Covariates	Sample size	Parameters	AAB	RMSE	AAB	RMSE
2	3	0	500	16	0.046	0.068	0.102	0.136
			1,000	16	0.022	0.032	0.055	0.071
			3,000	16	0.011	0.015	0.018	0.023
		1	500	18	0.031	0.041	0.065	0.091
			1,000	18	0.018	0.023	0.029	0.041
			3,000	18	0.007	0.010	0.011	0.015
	6	0	500	28	0.041	0.059	0.102	0.137
			1,000	28	0.019	0.028	0.052	0.068
			3,000	28	0.007	0.010	0.018	0.023
		1	500	30	0.020	0.028	0.089	0.119
			1,000	30	0.013	0.021	0.042	0.056
			3,000	30	0.007	0.009	0.014	0.019
3	3	0	500	25	0.055	0.074	0.143	0.197
			1,000	25	0.026	0.037	0.079	0.108
			3,000	25	0.014	0.017	0.023	0.030
		1	500	28	0.046	0.076	0.099	0.143
			1,000	28	0.019	0.027	0.053	0.075
			3,000	28	0.009	0.012	0.016	0.023
	6	0	500	43	0.030	0.042	0.111	0.148
			1,000	43	0.013	0.018	0.058	0.077
			3,000	43	0.007	0.009	0.019	0.025
		1	500	46	0.031	0.042	0.091	0.124
			1,000	46	0.014	0.020	0.046	0.062
			3,000	46	0.008	0.010	0.014	0.020

Note. AAB represents averaged absolute bias; RMSE represents root mean square error.

Table 4.

ML and Bayesian Estimation Performances for Multilevel MIRT Models

					Parameters vs. ML estimates		Parameters vs. Bayesian estimates
Factors	Items	Covariates	Sample size	Parameters	AAB	RMSE	AAB	RMSE
2	3	0	500	16	0.062	0.086	0.102	0.137
			1,000	16	0.030	0.048	0.052	0.069
			3,000	16	0.026	0.042	0.023	0.030
		1	500	18	0.039	0.055	0.078	0.106
			1,000	18	0.025	0.041	0.043	0.056
			3,000	18	0.022	0.040	0.013	0.017
	6	0	500	28	0.045	0.059	0.107	0.141
			1,000	28	0.031	0.043	0.052	0.068
			3,000	28	0.025	0.039	0.020	0.026
		1	500	30	0.033	0.046	0.069	0.094
			1,000	30	0.024	0.038	0.034	0.046
			3,000	30	0.022	0.037	0.012	0.017
3	3	0	500	25	0.053	0.076	0.141	0.187
			1,000	25	0.029	0.039	0.078	0.102
			3,000	25	0.025	0.033	0.027	0.034
		1	500	28	0.059	0.112	0.089	0.133
			1,000	28	0.030	0.046	0.048	0.071
			3,000	28	0.023	0.032	0.017	0.026
	6	0	500	43	0.047	0.071	0.116	0.151
			1,000	43	0.039	0.061	0.057	0.076
			3,000	43	0.031	0.048	0.015	0.021
		1	500	46	0.034	0.051	0.094	0.128
			1,000	46	0.029	0.044	0.049	0.066
			3,000	46	0.023	0.033	0.017	0.024

Note. AAB represents averaged absolute bias; RMSE represents root mean square error.

The simulation results for MIMIC models are presented in Tables 5 and 6. The AABs and RMSEs were relatively smaller than those in the simulation results for the MIRT models. There were also some noticeable patterns. First, the performances of both ML and Bayesian estimation methods improved as sample sizes increased from 500 to 3,000 and as the number of covariates increased from 1 to 2. The improvement with the increased sample size was quite predictable, but the improvement with the increased number of covariates was unexpected and interesting. Second, the numbers of items and factors did not affect the performances of the estimators in any single direction, which was different from the MIRT results. They affected the accuracy of the estimators positively in some conditions, but negatively in other conditions. Lastly, there were very minimal differences between the estimators in single-level MIMIC models, and the actual AABs and RMSEs were also much smaller compared to the values for single-level MIRT models. However, in multi-level MIMIC models, the performance differences between the estimators were obvious overall; the Bayesian results were better than the ML results.

Table 5.

ML and Bayesian Estimation Performances for Single-Level MIMIC Models

					Parameters vs. ML estimates		Parameters vs. Bayesian estimates
Factors	Items	Covariates	Sample size	Parameters	AAB	RMSE	AAB	RMSE
1	3	1	500	9	0.004	0.007	0.008	0.010
			1,000	9	0.005	0.003	0.006	0.007
			3,000	9	0.002	0.003	0.002	0.002
		2	500	10	0.005	0.008	0.007	0.009
			1,000	10	0.003	0.004	0.004	0.005
			3,000	10	0.001	0.001	0.003	0.003
	6	1	500	15	0.003	0.004	0.006	0.009
			1,000	15	0.002	0.003	0.003	0.003
			3,000	15	0.001	0.002	0.001	0.002
		2	500	16	0.003	0.005	0.004	0.005
			1,000	16	0.003	0.003	0.003	0.003
			3,000	16	0.001	0.001	0.001	0.001
2	3	1	500	18	0.004	0.005	0.007	0.009
			1,000	18	0.003	0.005	0.004	0.004
			3,000	18	0.002	0.002	0.001	0.002
		2	500	20	0.005	0.008	0.006	0.008
			1,000	20	0.003	0.003	0.003	0.004
			3,000	20	0.001	0.002	0.001	0.001
	6	1	500	30	0.004	0.006	0.008	0.010
			1,000	30	0.003	0.004	0.005	0.006
			3,000	30	0.001	0.002	0.002	0.002
		2	500	32	0.002	0.003	0.005	0.007
			1,000	32	0.003	0.004	0.003	0.004
			3,000	32	0.001	0.002	0.001	0.002

Note. AAB represents averaged absolute bias; RMSE represents root mean square error.

Table 6.

ML and Bayesian Estimation Performances for Multilevel MIMIC Models

					Parameters vs. ML estimates		Parameters vs. Bayesian estimates
Factors	Items	Covariates	Sample size	Parameters	AAB	RMSE	AAB	RMSE
1	3	1	500	9	0.017	0.022	0.008	0.011
			1,000	9	0.015	0.020	0.005	0.006
			3,000	9	0.016	0.020	0.002	0.002
		2	500	10	0.015	0.019	0.007	0.010
			1,000	10	0.013	0.017	0.004	0.005
			3,000	10	0.011	0.015	0.002	0.003
	6	1	500	15	0.027	0.037	0.005	0.008
			1,000	15	0.025	0.034	0.003	0.004
			3,000	15	0.025	0.033	0.001	0.002
		2	500	16	0.017	0.023	0.004	0.005
			1,000	16	0.017	0.023	0.002	0.002
			3,000	16	0.017	0.022	0.001	0.001
2	3	1	500	18	0.028	0.035	0.007	0.009
			1,000	18	0.026	0.034	0.003	0.005
			3,000	18	0.025	0.033	0.001	0.002
		2	500	20	0.019	0.025	0.005	0.007
			1,000	20	0.018	0.024	0.002	0.003
			3,000	20	0.019	0.025	0.001	0.001
	6	1	500	30	0.050	0.064	0.007	0.010
			1,000	30	0.046	0.059	0.004	0.006
			3,000	30	0.042	0.054	0.001	0.002
		2	500	32	0.031	0.040	0.005	0.007
			1,000	32	0.031	0.039	0.003	0.004
			3,000	32	0.029	0.037	0.001	0.002

Note. AAB represents averaged absolute bias; RMSE represents root mean square error.

The simulation results for the single- and multi-level MIRT models under high complexity are presented in Table 7. There were up to 180 dichotomous items and nearly 400 free parameters in a single model. As a result, the AABs and RMSEs were somewhat larger than the values for single- or multi-level MIRT models in Tables 3 and 4. However, as the sample size increased from 500 to 3,000 or from 1,000 to 3,000, the AABs and RMSEs decreased very fast, and they looked quite acceptable when compared to the previous results. The single- and multi-level results were also comparable; the multilevel specification did not make the model more complex in terms of AABs and RMSEs. One interesting finding in the single-level results was that, as opposed to the results in Tables 3 and 4, the estimation quality was worse with more items per factor under this high complexity. Too many items per factor in this particular settings did not help the accuracy of estimation.

Table 7.

Bayesian Estimation Performance for MIRT Models under High Complexity

						Parameters vs. Bayesian estimates
Model	Factors	Items	Covariates	Sample size	Parameters	AAB	RMSE
Single-Level	3	30	1	500	190	0.162	0.232
				1,000	190	0.084	0.123
				3,000	190	0.029	0.050
		60	1	500	370	0.264	0.378
				1,000	370	0.141	0.202
				3,000	370	0.043	0.062
	6	15	1	500	208	0.147	0.202
				1,000	208	0.077	0.105
				3,000	208	0.026	0.036
		30	1	500	388	0.182	0.257
				1,000	388	0.092	0.130
				3,000	388	0.029	0.040
Multilevel	3	30	1	1,000	190	0.088	0.122
				3,000	190	0.029	0.041
	6	15	1	1,000	208	0.077	0.106
				3,000	208	0.027	0.037

Note. AAB represents averaged absolute bias; RMSE represents root mean square error.

In summary, the performance of Bayesian estimation with diffuse priors was comparable to the performance of ML estimation with robust standard errors, even in multilevel modeling settings. Under the simulation conditions studied, ML estimation performed better for some and Bayesian estimation performed better for others. Bayesian estimation of single- and multi-level MIRT models under high complexity conditions also showed reasonably acceptable results when sample size was large (N = 3,000). The purpose of this simulation study was to check whether the Bayesian estimation with diffuse priors could be used as an alternative to the ML estimation in the MIRT and MIMIC models. Even without prior knowledge about the parameters (i.e., with non-informative priors), Bayesian estimation produced quite reliable results compared to ML estimation.

Conclusions

Initially, the present study started with a very important motivating data example, the MBE data that had multiple subtest areas and many categorical items. ML estimation failed to converge with an MIRT model that had six dimensions and 174 binary items, probably due to model complexity, but a Bayesian estimation method¹¹ was successful as an alternative to the ML estimation. The purposes of the present study were to verify whether Bayesian estimation with diffuse priors could be used as an alternative to ML estimation in the MIRT and MIMIC models, and to compare the practical usefulness of the two models with real data. To achieve the aims of the study, we first provided a real data analysis utilizing the motivating MBE data and Bayesian estimation with diffuse priors, and we then performed a Monte Carlo simulation study under various simulation conditions. Through the Bayesian real data analysis, we compared the MIRT and MIMIC models by estimating multiple ability factors or a total ability factor and examining the structural relationships among those factors, covariates, and/or an outcome variable with the MBE data. For the simulation study, the precision of the two estimators was evaluated under various simulation settings through the AAB and RMSE indices.

The real data analyses with the MBE data resulted in some similarities across the MIRT model and the MIMIC model. First, the relationship between the covariates (UGPA and LSAT) and the outcome variable (pass or fail) was fully mediated by the ability factors: the six specific ability factors in the MIRT model and the total (general) ability factor in the MIMIC model. In other words, there were statistically significant relationships between the covariates and the ability factors, and between the ability factors and the outcome variable. The relationship between the covariates and the outcome variable was suppressed even up to the significant negative association in our particular examples. Second, the single- and multi-level results were quite comparable regardless of the modeling types. The parameter estimates of the single-level models were fairly similar to the within-part parameter estimates of the multilevel models. That is, there were small multilevel effects, indicating a low ratio of between-state variances to total variances across indicator variables. This was also supported by the small intraclass correlation estimates of subtest scores that were previously shown in the multilevel MIMIC model.

Although the structural relationship results of the MIRT and MIMIC models were fairly comparable, there were some advantages of using the more complicated MIRT models over the simpler MIMIC models. First, the MIRT models provided some item-level analysis results. That is, we were able to identify the three items showing non-significant discriminations, implying that they did not measure their corresponding dimensions very well. Second, the MIRT models provided the tests for structural relationships among specific ability factors, covariates, and the outcome variable. For example, the MIRT model applied to the MBE data identified that one of the subtest domains, the RLP factor, did not predict the outcome variable very well.

We were able to compare the similarities and advantages among the MIRT and MIMIC models by adopting Bayesian estimation with diffuse priors because ML estimation failed. Verification was necessary because the performance of Bayesian estimation in these models in the SEM framework was not yet fully examined to the best of our knowledge. A Monte Carlo study was carried out to check whether Bayesian estimation with non-informative priors could be used as an alternative to ML estimation. The simulations were performed across the MIRT and MIMIC models under some limited conditions. The Bayesian estimation results were quite comparable to the ML estimation results according to the AABs and RMSEs. Even with non-informative priors, Bayesian estimation performed overall better than ML estimation especially when sample sizes were large (N = 3,000) and multilevel structures were considered. Because this was a simulation study, interpretation of and generalization from the results are by the limited settings. Nevertheless, the findings support that Bayesian estimation with diffuse priors may be a realistic alternative to ML estimation, particularly when ML fails. In other words, when ML is nearly impossible, such as with the case of the MIRT model utilizing the MBE data, Bayesian estimation may be used as an alternative to, or possibly better choice than, ML.

The present study demonstrated that if ML estimation failed due to model complexity, Bayesian estimation with diffuse priors could be used as a reliable substitute in the MIRT and MIMIC models. This study also compared the practical usefulness of the MIRT and MIMIC models by analyzing the MBE data example with Bayesian estimation. For the investigation of multiple ability factors, the MIRT model in the SEM framework would be a good choice because it permits item-level and specific factor analyses. However, the MIMIC model may be a simpler alternative to the MIRT model when one examines only a general ability factor and is not interested in item-level or specific factor analysis.

Appendix. Mplus Default Specifications for Diffuse Priors for the MIRT and MIMIC Models

For the Bayesian estimation with default diffuse priors of the MIRT and MIMIC models using Mplus 6 (Muthén & Muthén, 2010), three kinds of distributions were used: a normal distribution, an inverse gamma distribution, and an inverse Wishart distribution. Briefly, the normal distribution is specified as N(μ, σ²), and the density function is:

$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}.$$

The inverse gamma distribution is specified as IG(α, β), and the density function is:

$$f(x)=x^{-\alpha -1}{e}^{-\frac{\beta }{x}}.$$

The inverse Wishart distribution is specified as IW(Ω, d), where Ω is a positive definite matrix of size p and d is an integer, and the density function is:

$$f(\mathrm{\sum })={\mid \mathrm{\sum }\mid }^{\frac{-(d+p+1)}{2}}{e}^{-\frac{TR(\mathrm{\Omega }{\mathrm{\sum }}^{-1})}{2}}.$$

For more details, see Asparouhov and Muthén (2010).

For the single-level MIRT models, the priors for the loading values were N(0,5); the priors for the regression coefficients of the ability factors on the covariates were N(0, ∞); the priors for the regression coefficients of the outcome on the ability factors and the covariates were N(0,5); the priors for the covariances between the ability factors were IW(0,7); and the priors for the thresholds of the items were N(0,5).

For the multilevel MIRT models, in the within model, the priors for the loading values were N(0,5); the prior for the variance of the group variable was IG(−1,0); the priors for the regression coefficients of the ability factors on the covariates were N(0, ∞); the priors for the regression coefficients of the outcome on the ability factors and the covariates were N(0,5); and the priors for the covariances between the ability factors were IW(0,7). In the between model, the prior for the mean of the group variable was N(0, ∞); the priors for the residual variances of the items were IG(−1,0); and the priors for the thresholds of the items were N(0,5).

For the MIMIC models, the priors for the intercepts of the indicators (subtest scores) were N(0, ∞); the priors for the loading values were N(0, ∞); the priors for the covariances between the indicators were IG(−1,0); the priors for the regression coefficients of the ability factor on the covariates were N(0, ∞); the priors for the regression coefficients of the outcome on the ability factor and the covariates were N(0,5); and the priors for the thresholds of the outcome were N(0, ∞).

For the multilevel MIMIC models, in the within model, the priors for the loading values were N(0, ∞); the priors for the covariances between the indicators were IG(−1,0); the priors for the regression coefficients of the ability factor on the covariates were N(0, ∞); and the priors for the regression coefficients of the outcome on the ability factor and the covariates were N(0,5). In the between model, the priors for the loading values were N(0, ∞); the priors for the residual variances of the indicators were IG(−1,0); the prior for the variance of the outcome was IG(−1,0); and the prior for the threshold of the outcome was N(0, ∞).