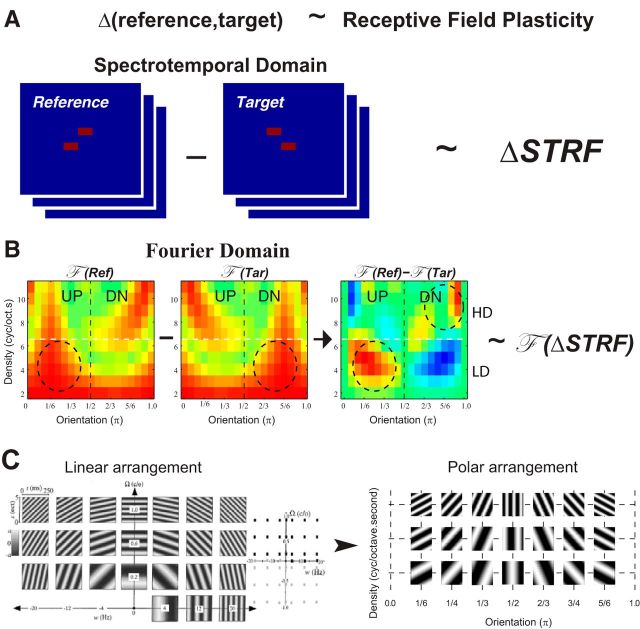
Figure 2.
The matched filter hypothesis and polar Fourier representation. A, Schematic of the predictions of the matched filter hypothesis. Rapid receptive field plasticity during behavior is predicted to reflect the difference between the discriminated reference and target sounds: Δ(reference, target). Animals attended to a spectrotemporal difference: the direction of pitch shift in tone pairs that have random absolute frequencies. Consequently, plasticity is predicted to reflect the change in pitch direction via ΔSTRF of the responding neurons. B, The 2D polar Fourier transforms of the two-tone sequences. The stimuli, STRFs, and ΔSTRFs can be better visualized through their Fourier transforms, which specifically highlight the directional information in the stimuli through their asymmetry around the midline. In general, directionally shifting stimuli or tilted STRFs exhibit an asymmetric Fourier transforms. For the tone pairs, the asymmetry is reversed in the LD and HD regions, which are separated by the white horizontal line in the panels. Because of the “aversive” nature of the reference stimuli (compared with the “appetitive” target), the asymmetry of the Fourier transforms of ΔSTRF (denoted by F(ΔSTRF)) is predicted to match the asymmetry pattern of the Fourier transform of the difference of the reference and target stimuli: F (Ref) − F (Tar). The example shown represents the case when the reference (target) stimulus is the up-shifting (down-shifting) tone sequence. C, All Fourier transforms shown are plotted on a polar grid, which spreads them out more evenly and clearly. The sinusoidal spectra (called “ripples”) are the basis functions of the Fourier transform of the spectrotemporal stimulus and STRF patterns. Left panels, Normal distribution of ripple coefficients in the Fourier domain, with positive rates (ω) and spectral densities (Ω) corresponding to downward-moving ripples, and negative rates to upward-moving ripples. In the polar Fourier transform, the coefficients of the ripples are simply rearranged on a grid such that all ripples in a given column have the same orientation (π) and are organized from 0 to π orientations. They are arranged with increasing density up the ordinate.