FIG. 3.

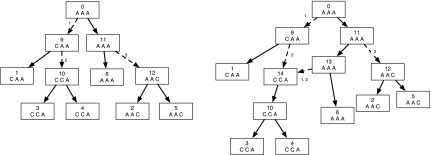
Example of a character dataset that displays a tree that models better than networks with reticulate vertices. The input set of three characters on two states “A” and “C” are given in the leaves. It can be seen that there is perfect phylogeny for this set of characters, namely, there is a tree (on the left) such that each of its internal edges splits a unique character into the two states (the edges that split the different characters are shown in dotted lines with the corresponding character site written next to each of them). Thus the tree is an optimal tree with parsimony cost of three, which equals the number of characters. Note that this is the minimum cost that can be attained for this dataset. Shown on the right is a network with the same input dataset. The softwired and adjusted hardwired parsimony costs of the network is three. However, it can be noted that the reticulate vertex 14 is redundant since the edge (13, 14) may be removed to render the same cost. In general, the network cost of this dataset on any network with at least one reticulate vertex will either have a cost of four or higher or if the score is three, then the set of all its reticulate vertices will be redundant. Thus the score on the left hand tree is better than the score on the right.