Figure 2. Log-log plot of the unified 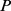-value vector versus the rank vector .

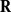The curves in panels (A) and (B) were obtained from combining the 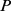-values of four 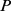-value vectors, each of size 10,000, using Stouffer's method. In panel (A), the red circles show the scatter plot of normalized rank versus computed 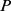-value from a randomly picked iteration (realization) of very weak average correlation. It is through curves like the one displayed in panel (A) that enables one to calculate the average sum of squares error using eq. (15) and the distance measure using eq. (16). Panel (B) shows 1000 curves, each of which is obtained from performing the same task as that leads to the curve in (A) but with different average correlation strengths. The lines that go significantly above line are from cases with stronger average correlations. They yield unified 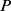-values that are much exaggerated perhaps due to the fact that the Stouffer's method does not account for correlations. 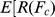By averaging the normalized rank along the blue line () yields the value (see eq. (17)). By shifting the blue line to different values renders the entire versus curve. The red horizontal line illustrates the case when (or normalized rank ). 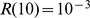By averaging the 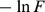values along this line, the value is obtained for by simply adding to the averaged value (see eq. (18)).