Fig. 3.
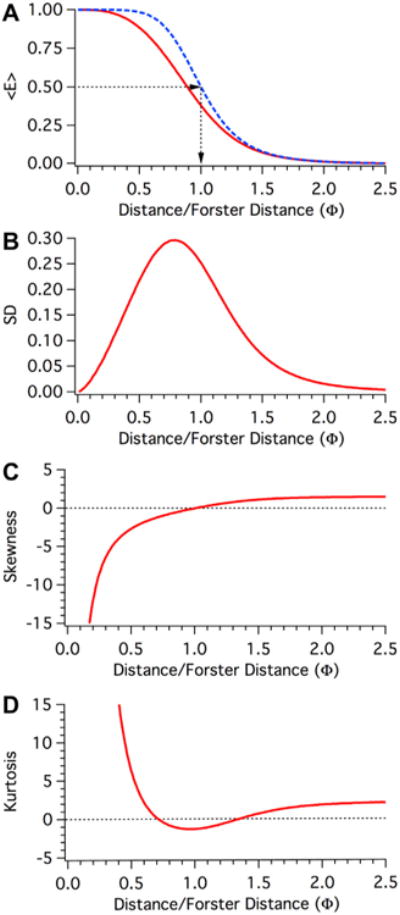
Moment Analysis of the dependence of FRET efficiency on Separation under static isotropic conditions. A. The dependence of 〈E〉 (the first moment of these populations) on Φ under isotropic dynamic (dashed Blue) or static (Red) conditions. (B) The dependence of variance (the second moment) on Φ under isotropic static conditions (Red). Plotted is the standard deviation of the distribution, which is the positive square root of the variance. (C) The dependence of skewness (the third moment) on Φ under isotropic static conditions (Red). The skewness represents symmetry within the distribution; a positive value indicates a heavier tail to the right, while a negative value indicates a left skewed distribution. (D). The dependence of kurtosis (the fourth moment) on Φ under isotropic static conditions (Red). The kurtosis represents the distribution peakedness relative to a normal distribution. A positive value indicates an acute peak in the distribution, while a negative value indicates a broad flat distribution.
