Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.
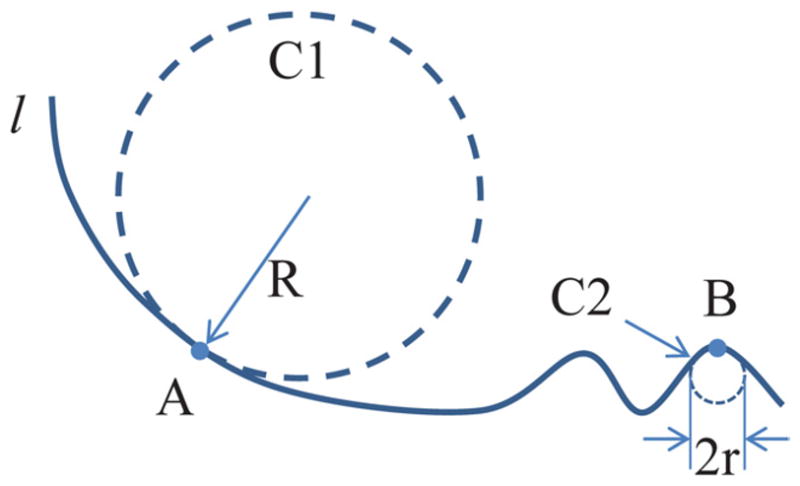
Relationship between curvature and roughness. Curvature of point (A and B) on line (l) can be defined as reciprocal of circle radius, eg radius (R) for large circle (C1) and radius (r) for small circle (C2), which is tangent to point and more tightly close to line. Smooth section of line (around A) has smaller curvature than rough section (around B). Thus, curvature is natural way to quantify roughness. It was used in our study to analyze kidney stone surface morphology.
