Fig. 2.
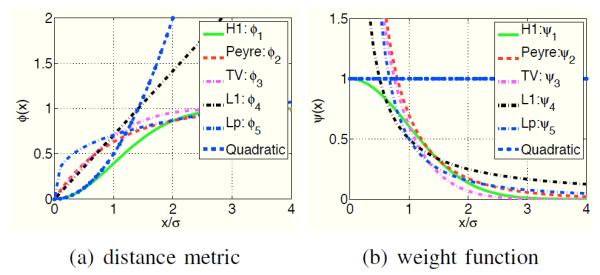
Comparison of the distance metrics ϕ and corresponding weight functions ϕ: The different distance metrics and the weight functions are plotted in (a) and (b), respectively. Note that the convex distance functions, shown by the blue and black curves, do not saturate with the Euclidean interpatch distances. In contrast, the distance functions corresponding to the current nonlocal schemes saturate as the patches become dissimilar. This ensures that the distances between dissimilar patches are not penalized, thus minimizing the blurring compared to the convex choices. This is also observed by the weights in the sum in (6). Note that the weights associated with the current schemes decay to zero for large distances. The slow decay of the weights associated with the convex metrics can result in blurred reconstructions. The lp; p = 0.3 norms saturate rapidly, when compared to other non-local metrics, resulting in reduced averaging of similar patches.
