Fig. 4.

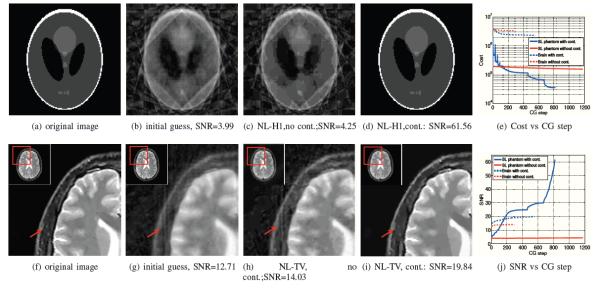
Utility of continuation: We consider the recovery of a 128x128 Shepp Logan phantom from its ten radial lines in the Fourier domain in (a)-(d). The classical alternating algorithm emphasizes the alias artifacts in the initial guess in (b), which is obtained by zero-filled IFFT. Specifically, the result in (c) correspond to a local minimum of (12). The use of the continuation scheme mitigated these issues as seen in (d). We also consider the reconstruction of a 256 × 256 MRI brain image from 46 uniformly spaced radial lines in the Fourier domain. We observe that the alternating algorithm results in the enhancement of the alias artifacts (see (h)). These problems are eliminated by the continuation scheme, shown in (i). The behavior of the algorithms can be better understood from the cost vs iterations shown in (e). It is observed that the continuation schemes shown in blue solid and dotted lines (corresponding to Shepp-Logan and brain images, respectively) converge to a lower minimum than the methods without continuation (red solid and dotted lines). The improvement in performance is also SNR vs CG step plot in (j).