Pattern Transformation with DNA Circuits

Abstract

Readily programmable chemical networks are important tools as the scope of chemistry expands from individual molecules to larger molecular systems. While many complex systems have been constructed using conventional organic and inorganic chemistry, the programmability of biological molecules such as nucleic acids allows for precise, high-throughput, and automated design, as well as simple, rapid, and robust implementation. Here we show that systematic and quantitative control over the diffusivity and reactivity of DNA molecules yields highly programmable chemical reaction networks (CRNs) that execute at the macroscale. In particular, we design and implement non-enzymatic DNA circuits capable of performing pattern transformation algorithms such as edge detection. We also show that it is possible to fine-tune and multiplex such circuits. We believe these strategies will provide programmable platforms for prototyping CRNs, for discovering bottom-up construction principles, and for generating patterns in materials.

Introduction

The inherently modular and programmable nature of chemical reactions can be exploited to create complex systems. On the molecular- and nano-scale, it is possible to construct supramolecular structures and machines^1,2, as well as to control the formation of nanoscale morphologies^3-5. On the macroscopic scale, complex chemical reaction networks (CRNs) have been rationally built to exhibit non-linear dynamics^6-8. The classic example of these CRNs, the Belousov-Zhabotinsky (BZ) oscillation⁹, has been parameterized and/or derivatized to exhibit a variety of novel and emergent behaviors^7,10-12. The versatility of such CRNs has not only inspired bottom-up engineering across scales¹³, but also led to proposals for ‘chemical computers’^14,15.

However, conventional CRNs are difficult to reprogram. Association and bonding are often idiosyncratic and not amenable to redesign. In contrast, at least some components from biology, such as nucleic acids, are highly programmable. This has been reflected in the rise of DNA nanotechnology and in particular the engineering of nanoscale, high-resolution, arbitrarily-shaped 2D and 3D structures¹⁶. In a series of recent demonstrations, over 200 distinct 2D and 3D nanostructures with complex features were built from only two sets of building blocks in separate one-pot annealing reactions^17,18. Mobile DNA devices such as walkers^19,20 and assembly lines²¹ based on these defined-shape structures have also been constructed.

The development of completely programmable reactions with DNA, based in part on the recent development of enzyme-based^22-25 and enzyme-free^26-29 DNA circuitry, suggests that it should be possible to build complex DNA CRNs. Winfree and coworkers have already established facile schemes to realize arbitrary CRNs using strand displacement-based DNA circuits, where essentially all the thermodynamic and kinetic parameters can be tuned over 4 orders of magnitude³⁰. Similar circuits have already been shown to be capable of performing complex Boolean and neuron-like computations in well-mixed solutions^31,32.

We now expand the capability of such circuits to produce macroscale spatial patterns via programmed reaction-diffusion processes. In particular, we have created circuits capable of pattern transformation (or image processing), which is a well-established benchmark for testing the programmability of CRNs³³ and even cell-based gene regulatory networks (GRNs)^34,35. As an example, we have implemented light-directed enzyme-free DNA circuits that perform edge detection (also called contour discernment³³). Simply speaking, the edge detection circuit converts a binary (i.e. black-and-white) input pattern into a new pattern in which only the black-white boundary of the original pattern is highlighted (Figure 1a). We have further shown that we can rationally alter the components and connectivity of the underlying, nanoscale CRNs so that image processing at the macroscale becomes completely programmable. Several aspects distinguish these circuits from most of the previous pattern-generating CRNs based on oscillatory reactions, like the BZ reaction. First, the thermodynamics, kinetics, and specificity of individual reactions are all specified de novo by the designer and then implemented in artificially designed molecules. Second, these circuits do not rely on oscillatory reactions but are based on much simpler linear catalytic reactions. Third, for the simplicity of design, positive and negative feedbacks were not engineered in these circuits. As a result, these circuits do not generate patterns from near-homogeneity but reliably transform a pre-specified input pattern to different output patterns.

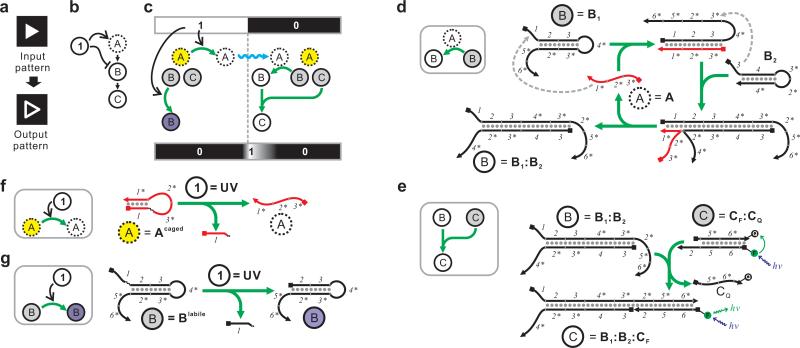
Figure 1.

High-level description and molecular detail of an incoherent feed-forward loop that performs edge detection. (a) Definition of edge detection with a binary input. (b) High-level description of the incoherent feed-forward loop. The input signal is denoted as “1”. The only fast-diffusing species (“A”) is denoted with a dashed circle. (c) Detailed mechanism of the incoherent feed-forward loop. The input signal can turn caged A (yellow) into active A (white) and simultaneously turn inactive B (gray) into ablated B (unable to be activated by A, purple). Activated A can then diffuse (blue squiggle) to the area where input signal is absent (= 0) and turn inactive B (gray) into active B (white). Active B can then combine with inactive C (gray) to form active C (white) near the 1/0 boundary. (d-e) Implementation of the circuit shown in (c) using a CHA circuit. Active A, inactive B, and active B are represented by A, B₁, and the B₁:B₂ duplex, respectively. For simplicity B₂ is not shown in (c). A can catalyze the formation of the B₁:B₂ duplex through the depicted pathway. Inactive C is represented by the C_F:C_Q duplex, where the fluorescence is quenched. Active C is represented by the B₁:B₂:C_F complex, where the fluorescence is unquenched. Domains 1, 2, 3, 5, and 6 are 8-nt long; domain 4 is 11-nt long. See Supplementary Table S1 and Supplementary Figure S8a for sequences. (f) Mechanisms of the photo-activation of A^caged. (g) Mechanisms of the photo-ablation of B₁^labile. See Supplementary Figure S1a for chemical structure of the photo-cleavable linker.

Ultimately, such bottom-up, designed CRNs may find various applications in areas as diverse as synthetic biology, tissue engineering, and materials science.

Results

The underlying logic of the edge detection circuit

To achieve edge detection using CRN, one simply needs to construct an incoherent feed-forward loop. Figure 1b describes one form of such logic. In this form, the input signal (noted as “1”) can be received by two chemical species “A” and “B.” “A” is activated by the input signal whereas “B” is inhibited by the input signal. “A” also activates “B” by turning “B” into “C.” As a result, the input signal “1” activates the formation of “C” through the “1-A-B-C” pathway, but inhibits the formation of “C” through the “1-B-C” pathway. Hence such a feed-forward loop is considered ‘incoherent’.

As illustrated in Figure 1c, when the input pattern is delivered as the input signal (“1” and “0” means the presence and absence of the input signal, respectively) and “A” diffuses much faster than “B” and “C”, “C” will be produced only near the “1/0” boundary of the input pattern, resulting in an edge. The reason is fairly intuitive. In the area where the input signal is present, “C” cannot be produced since “B” is inhibited. Similarly, in the area where input signal is absent, “C” cannot be produced either since “A” is not activated. Near the boundary, “A” activated by the input signal can diffuse into the area without input signal to react with “B” and form “C.” The edge will broaden over time as “A” diffuses deeper into the area without input signal.

Chemical implementation of the edge detection circuit

We implemented this CRN with an enzyme-free DNA circuit (Figure 1d-g). To facilitate description, we use the following naming convention. DNA species are named in the form of ‘X_Y^Z’, where the subscript and superscript are optional. The main name “X” describes the general function of the species and is consistent with the high level descriptions shown in Figures 1c and 2b. The subscript “Y” identifies the subunit. For example, B₁ and B₂ are the two subunits of B. The superscript “Z” identifies any modification. For example, A^caged is a modified version of A that can be photo-activated.

Figure 2.

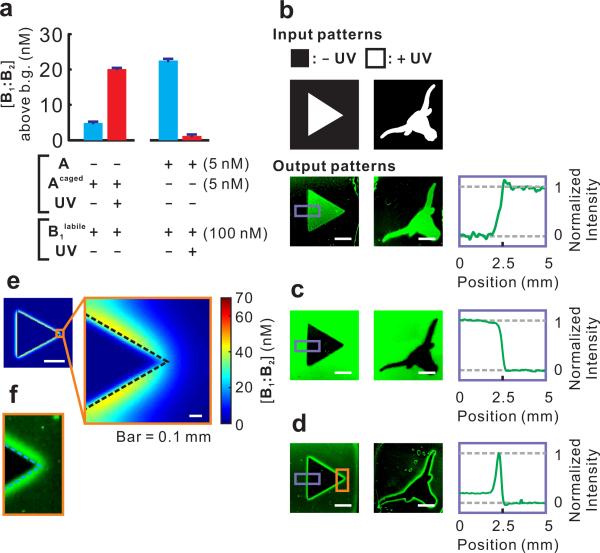
Execution of the incoherent feed-forward loop that performs edge detection. (a) Photo-activation of A^caged and photo-ablation of B₁^labile measured in solution. Concentrations of B₂ and C_F:C_Q were 150 nM and 100 nM, respectively, in all reactions. The concentrations of product B₁^labile:B₂ above background (uncatalyzed formation of B₁^labile:B₂, ~10 nM) after 3 h are shown in the bar graph. Error bars (in many cases lower than the width of the horizontal bars) show the standard deviations of 6 measurements taken at the end of the reaction. See Supplementary Figure S1b-c for real-time fluorescence measurements. (b) Positive images obtained with A^caged only. (c) Negative images obtained with B₁^labile only. (d) Edge detection achieved with A^caged and B₁^labile. In b to d, plots of the fluorescent signal versus position in the highlighted area (purple box) are shown in the right panels. (e) Simulation of the edge detection circuit. See Supplementary Method S2. (f) Zoom-in of the highlighted area (in the orange box) of (d). Dashed line approximately indicates the position of the actual light-dark boundary. Unless otherwise stated, in all images scale bar = 3 mm.

The core of the circuit is a hybridization-based signal-amplification reaction²⁸ which has been termed catalyzed hairpin assembly^36,37 (CHA, Figure 1d). In this reaction, strand A (representing “A” in Figure 1c) catalyzes the hybridization between hairpins B₁ (representing the inactive, gray “B” in Figure 1c) and B₂ to form the B₁:B₂ duplex (representing the activated, white “B” in Figure 1c). This duplex can then react with a reporter construct C_F:C_Q (Figure 1e, representing the inactive, gray “C” in Figure 1c) and form a fluorescent tripartite complex B₁:B₂:C_F (representing the activated, white “C” in Figure 1c).

We used UV (365 nm) as the input signal. To implement the activating role of UV, we replaced strand A with A^caged, which adopts a conformer that prevents its interaction with the domain 1 of its hairpin substrate B₁ (Figure 1f). A^caged includes a photo-cleavable (365 nm) linkage (Supplementary Figure S1a) that allows photo-uncaging to produce A^uncaged, and thus initiation of the reaction (Figure 2a, Supplementary Figure S1b). When the circuit is executed in a heavily cross-linked media (20% polyacrylamide) all reactants including A^uncaged diffuse slowly enough that the CHA reaction occurs primarily within the illuminated area, leading to an increased fluorescent signal (Figure 2b). Therefore, these reactions together constitute a ‘photography’ (or ‘positive image’) circuit.

To implement an inhibitory role for the UV signal in the incoherent feed-forward loop, we further generated a photo-ablatable substrate (Figure 1g). The phosphodiester bond between the domains 1 and 2 of B₁ was replaced by a photo-cleavable linker to create B₁^labile such that exposure to UV light will remove the domain 1 and thus prevent any use of the substrate. We confirmed that B₁^labile could be completely ablated with UV exposure (Figure 2a, Supplementary Figure S1c). When B₁^labile was mixed with A, B₂, and C_F:C_Q, a ‘negative image’ circuit was created, where the output is the inverse of the input image (Figure 2c). When both the photo-activatable catalyst (A^caged) and photoablatable substrate (B₁^labile) are used in the same reaction, neither positive nor negative image can be created. Rather, the activated, diffusible catalyst can move to find new substrates, initiating a reaction cascade around the illuminated area and creating a fluorescent edge (Figure 2d). Given that cleaved A^caged diffuses much faster than intact B₁^labile (Supplementary Table S2), it was predicted (Figure 2e) and observed (Figure 2f) that the computed edge would predominantly localize on the dark side of the light-dark boundary, generating a ‘negative edge’. We built a systems-chemistry inspired mathematical model to quantitatively predict this system's behavior³⁸ and the experimental full-width at half-maximum (FWHM) was in good agreement with our numeric simulation (Supplementary Figure S2a). The resulting edge was determined to be ~ 0.5 mm with a trailing edge toward the dark area. It can be estimated that an illuminated strip as narrow as ~ 0.1 mm between two dark areas should result in two distinctive edges, as will a dark strip as narrow as ~ 0.8 mm between two illuminated areas. This is a ~ 10-fold higher resolution than the cell-based biological edge detector³⁵, largely due to the much slower diffusion of A^caged in 20% polyacrylamide gel than quorum-sensing molecules in agar. A striking feature of the edge detection circuit is that the output pattern is neither specified via the input pattern nor encoded in the underlying CRN, but rather emerges as these two factors interact. Such an emergent property exemplifies the feasibility of combining bottom-up nanoscale engineering with top-down specification.

Shifting the position of the computed edge

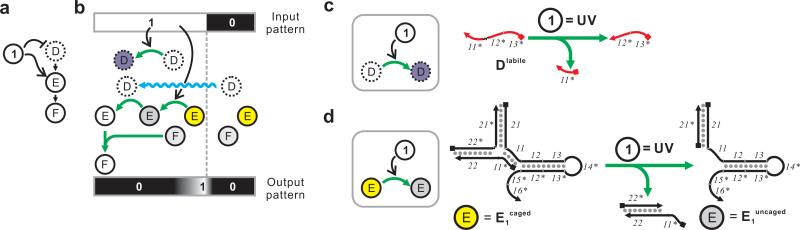
In order to show the programmability and modularity of the CRN-based pattern-transformation programs, we next attempted to generate a ‘positive edge’ (as opposed to the ‘negative edge’ described above) circuit where the computed edge predominantly localizes at the illuminated side of the boundary. As can be seen in simulations (Supplementary Figure S2b), the location of the edge is largely dependent on the relative diffusion coefficients of the photo-activated species (in this case A^caged) and the photo-ablated species (in this case B₁^labile). To generate the positive-edge circuit, we took a similar CHA reaction (Supplementary Figure S3), where D catalyzes the formation of a duplex from hairpins E₁ and E₂, and made it light responsive by reversing the logic previously applied (Figure 3): that is, the fast-diffusing catalyst D was replaced by its photo-ablated variant D^labile whereas slow-diffusing E₁ was replaced by its photo-activated variant E₁^caged. This way, intact D^labile from the dark area could diffuse to the illuminated area where it would encounter slow-diffusing, photo-activated E₁^uncaged, and produce the E₁^uncaged:E₂ duplex, which would in turn react with the reporter F_F:F_Q to produce the output signal E₁^uncaged:E₂:F_F. To engineer the photo-ablatable catalyst D^labile we replaced the phosphodiester bond between domains 11* and 12* with a photo-cleavable linker (Figure 3c). To engineer E₁^caged, we designed hairpin E₁ with a 20-nt extension (domain 21) and hybridized it to a duplex inhibitor that contained domain 11* which in turn blocked domain 11 of E₁ in a 3-way junction (Figure 3d). Upon photo-cleavage of the linker between domain 11* and the rest of the duplex inhibitor, domain 11* will dissociate from the complex, resulting in E₁^uncaged. We used this tripartite design for E₁^caged(rather than a linker-containing, self-inhibiting, single-molecule design, as in A^caged) in order to avoid the challenging synthesis of long (~90-nt) oligonucleotide containing a photocleavable linker. We confirmed that D^labile could be completely inactivated by light, while E₁^caged cannot function as a substrate until it is photo-cleaved (Figure 4a, Supplementary Figure S4). As anticipated, mixing the D^labile, E₁, E₂, and F_F:F_Q resulted in a new ‘negative image circuit’, while mixing the D, E₁^caged, E₂, and F_F:F_Q resulted in a new ‘positive image circuit’ (Figure 4b). Combining these two light-sensitive circuits (mixing D^labile, E₁^caged, E₂, and F_F:F_Q) immediately resulted in a new ‘positive edge circuit’ (Figure 2c).

Figure 3.

High-level description and molecular detail of the ‘positive edge’ circuit. (a) An incoherent feed-forward loop with inversed logic. (b) Detailed mechanism of the incoherent feed forward loop. Here D is ablated and E is activated by the input signal. Active, inactive, caged and ablated molecules are shown in white, gray, yellow and purple, respectively. (c) Mechanisms of the photo-ablation of D^labile. (d) Mechanisms of the photo-activation of E₁^caged. Domains 11, 13, 15, and 16 are 8-nt long; domain 12 is 11-nt long; domain 14 is 15-nt long; domains 21 and 22 are 20-nt long. See Supplementary Table S1 and Supplementary Figure S8b for sequences.

Figure 4.

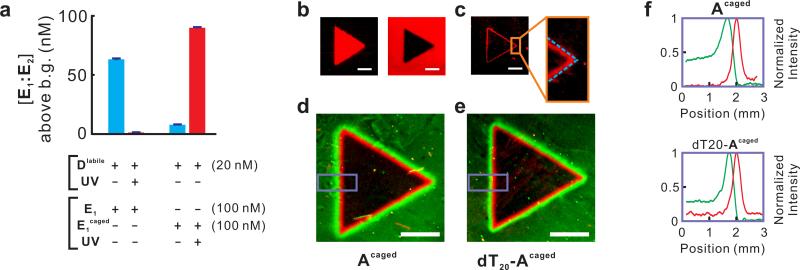
Execution of the ‘positive edge’ and ‘edge splitter’ circuits. (a) Photo-ablation of D^labile and photo-activation of E₁^caged measured in solution. Concentrations of E₂ and F_F:F_Q were 150 nM and 100 nM, respectively, in all reactions. The concentrations of product E₁:E₂ above background (uncatalyzed formation of E₁:E₂, ~8 nM) after 3 h are shown in the bar graph. Error bars (in many cases lower than the width of the horizontal bars) show the standard deviations of 6 measurements taken at the end of the reaction. See Supplementary Figure S4 for real-time fluorescence measurements. Note that the higher signals observed here (compared with Figure 2a) are mainly attributed to the higher concentration of catalyst (20 nM as opposed to 5 nM in Figure 2a). (b) Positive image (left) and negative image (right) obtained by E₁^caged only and D^labile only, respectively. (c) Edge detection achieved with E₁^caged and D^labile. Dashed line approximately indicates the position of the actual light-dark boundary. (d) Edge splitter program by combining the ‘negative edge’ program (reported by the green fluorophore FAM) and the ‘positive edge’ program (reported by the red fluorophore TYE665). (e) Use of dT₂₀-A^caged results in a negative edge narrower and closer to the positive edge. (f) Quantification of fluorescence signal in the areas highlighted by purple on d (top) and e (bottom). In all images scale bar = 3 mm.

Multiplexing edge detection circuits

The two families of CHA (catalyzed by A and D) circuits were designed to have unrelated sequences, and hence can readily operate orthogonally. The same orthogonality can be applied to differentiate the parallel execution of circuits and thereby create even more complex output patterns. We used two fluorophores, FAM (green) and TYE665 (red), to visualize the output of the first and second family of circuits, respectively. As an example, combining a red positive edge and a green negative edge (or vice versa) yielded an ‘edge splitter’ program where two separate lines reside on the opposite sides of the light-dark boundary were computed (Figure 2d).

Not only could we shift the position of the computed edge over a long distance by rewiring the circuit, we could also fine-tune the position and width of the edge by programming the diffusion properties of the reactants. For example, we created a slow-diffusing version of A^caged by extending it at the 3’ end with a (dT)₂₀ tail, which causes ~30% decrease in the diffusion constant (Supplementary Table S2). As expected, when this new catalyst (named dT₂₀-A^caged) was used in the ‘edge splitter’ program, it generated a negative edge ~ 0.1 mm closer to the positive edge (red) than its predecessor A^caged and was only ~ 50% as wide (Figure 4e-f).

The idea that we can program circuits via their individual diffusivity has a counterpart: that the circuits can be used to assay or detect changes in diffusivity. In particular, we had previously modeled that diffusivity within the matrix should directly impact the width of a computed line (Supplementary Figure S2c). To demonstrate diffusivity detection directly, we made a piece of inhomogeneous gel, where half of the gel was made using 20% polyacrylamide and half was made using 12% polyacrylamide. An input pattern of two rectangles was delivered by UV exposure, spanning the interface of the inhomogeneous gel. As anticipated the developing edges were quite different in the 20% portion of the gel relative to the 12% portion (Supplementary Figure S5). It is plausible that this or similar systems could be deployed for gross material testing, including analysis of crack formation.

Generality of the DNA-based edge detection circuit

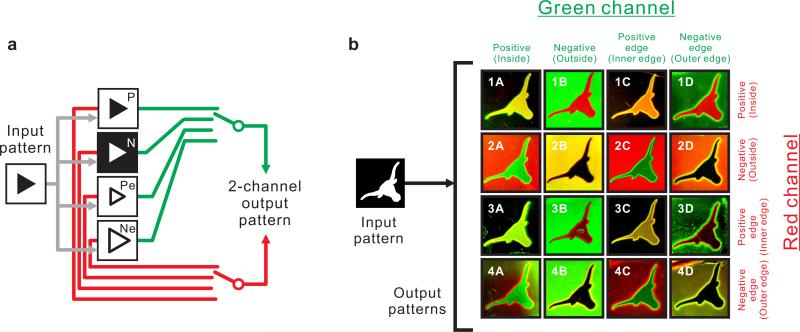
Finally, to showcase the generality of our circuits and methods we took a combinatorial approach to pattern-transformation. For a given input pattern, the A/B₁/B₂-based circuit could be configured to perform one of four possible transformations – positive image, negative image, positive edge, or negative edge – and generate output in the green channel; whereas the D/E₁/E₂-based circuit could be similarly configured, but to generate output in the red channel (Figure 5a). Therefore, a total of 16 possible combinations could be generated. Using the same input pattern, a Longhorn logo, we were able to obtain 16 distinct outputs, where the input/output transformations were completely governed by the components, programmed specificities, and reaction-diffusion kinetics of the chemical mixtures (Figure 5b). In some cases where the output patterns of the green channel and the red channel are identical (Figure 5b, Images 3C and 4D), the pattern transformation program was simplified by executing one circuit but connecting it to two reporters of two colors (Supplementary Table S3). While in general the programs executed exactly as designed, in some cases there was slight background (e.g. the green haze seen in the illuminated interiors of Images 2C and 4C). Even this noise had predictable properties in that it generally seemed to be associated with particular regions and particular circuits (e.g. illuminated regions for positive edge circuits and dark regions for the negative edge circuits). The origin of this background is discussed in Supplementary Methods.

Figure 5.

Combinatorial multiplexing of 2-channel pattern-transformation programs. (a) Scheme of the pattern-transformation programs. P: Positive image; N: Negative image; Pe: Positive edge; Ne: Negative Edge. (b) 16 different 2-channel output patterns generated from the same input pattern through 16 different pattern-transformation programs.

Discussion

This work demonstrates the first examples of fully programmable, reaction diffusion-based pattern transformation programs. Aside from the ability to rewire, fine-tune, and multiplex, the programmability of DNA-based CRN was crucial to the successful demonstrations in this work in other aspects. For example, the ability to program catalytic reactions (rather than simple, uncatalyzed hybridization) using DNA circuits was key to limiting the accumulation of background during UV exposure, which took 30 min. Using the A/B₁/B₂-based ‘negative edge’ circuit as an example, during UV exposure, the newly formed A^uncaged might react with B₁^labile that had not yet been ablated in the illuminated area, causing background. However, by designing the catalytic reaction we were able to limit this unwanted reaction to one turnover by carrying out the UV exposure at 4 °C (since at such a low temperature A^uncaged cannot dissociate from its product B₁^labile:B₂). Essentially the circuits were only turned on when the temperature was raised to 37 °C, after the completion of UV exposure.

Compared with E.coli-based genetic pattern-transformation programs³⁵, our circuits are not only much more modular, extensible, and predictable, but also incredibly compact. The edge detection circuit shown here only consists of 5 DNA molecules with a combined ~200-nt sequence, whereas the genetic circuit consists of 5 genes which add up to ~10-kb in length, not including the remaining megabases of information necessary for bacterial execution. In a sense we have compacted the bacterial circuit by ~ 50-fold.

The demonstrations shown in this work highlight the feasibility of designing macroscale morphologies through programmable nanoscale molecular interactions. This is a key demonstration in the nascent field of systems chemistry, which in part seeks to generate kinetically controlled systems in which the products of one reaction affect the rates of other reactions. Such CRNs can display complex, predictable behaviors,^39,40 including emergent properties normally associated with biology, such as pigmentation patterns on scales and shells^41,42. To a first approximation, the development of a DNA-based CRN that executes an amorphous computation in space is the first example of a truly multiscale technology in which empirical rule sets and quantitative models define the interconnectivities between scales⁴³. When combined with more complex DNA circuits^30-32 and functionalized DNA molecules⁴⁴ these approaches may yield not only patterns but architectures whose functionality emerges at length scales that impact organismal biology and materials science.

Methods

Chemicals and oligonucleotides

All chemicals used were analytical grade from Sigma-Aldrich (St. Louis, MO). DNA oligonucleotides were ordered from Integrated DNA Technologies (IDT, Coralville, IA). Unless HPLC purification was required by IDT (for certain modifications), all oligonucleotides were ordered as de-salted and then gel purified by denaturing (7 M urea) PAGE upon arrival. PAGE-purified oligonucleotides were stored at a stock concentration of 1 or 10 μM in 1x TE (pH 7.5). Reporter duplexes were generated by annealing 20 μM of quencher strand with 10 μM of fluorophore strand. Oligonucleotide sequences were designed using CircDesigNA (http://sourceforge.net/projects/circdesigna/) once circuit architecture and domain organizations were determined. Proper folding and hybridization of hairpins, duplexes, and multi-strand complexes were confirmed using NUPACK⁴⁵ (http://www.nupack.org/). A complete list of oligonucleotides can be found in Supplementary Table S1.

Solution assay of fluorescence

The kinetics of CHA circuits in solution were assayed using a Safire plate reader (TECAN, Männedorf, Switzerland) or a QuantiFluor-P fluorometer (Promega, Madison, WI). Each component was mixed separately in 1x TNaKT (20 mM Tris, pH 7.5; 140 mM NaCl; 5 mM KCl; 1 μM (dT)₂₁) and hairpins were folded separately immediately before use by heating to 90 °C for 2 minutes and ramp cooling at 0.1 °C/sec to 23 °C. All components and reagents were equilibrated at 37 °C for 30 minutes before mixing and initiation of the reaction. Components were mixed and the reaction started in each case by addition of the hairpin that directly interacts with the catalyst strand (e.g. B₁ and E₁^uncaged). After sufficient mixing, the reaction was transferred to a 384-well black polystyrene plate and the output fluorescence measured on a Safire plate reader. To assay circuit activity at 4 °C, all reagents were mixed as above and transferred to 4 °C for 30 minutes. After temperature equilibration the components were mixed and transferred to a 0.5 mL optically transparent Eppendorf tube. Fluorescence measurements were made using a single tube QuantiFluor-P Fluorometer maintained at 4 °C. For comparison and determination of the effect of temperature, the above procedure was repeated with reagents and the fluorometer maintained at 37 °C.

Gel assembly, exposure, and imaging

To form the gel box, a 200 μm-thick piece of acrylic was centered on top of a 75 × 25 mm glass slide (Gold Seal, Portsmouth, NH). A small bead of fast-setting epoxy (ITW Performance Polymers, Riviera Beach, FL) was placed along two sides of a No.1 22 x 22 mm coverslip (Erie Scientific Company, Portsmouth, NH) and the coverslip adhered to the glass slide over top of the acrylic spacer. After the epoxy set, the acrylic spacer was removed, and the two supporting sides of the coverslip further sealed with a bead of epoxy. The two ends at opposite sides of the gel box were left open for sample injection and ventilation. All reagents were then moved to 4 °C and allowed to equilibrate for 30 minutes. To form the gel, 40% acrylamide/bis (19:1) (BioRad, Hercules, CA), 6x TNaK (1x TNaK = 20 mM Tris, pH 7.5; 140 mM NaCl; 5 mM KCl), 1% ammonium persulfate, 10% TEMED, and the DNA components (see Supplementary Table S3) were mixed to yield a final gel of 20% acrylamide in 1x TNaK. After thorough pipette mixing, the mixture was transferred to the gel box on the glass slide. After a brief initial setting period, the open ends of the gel box were sealed with epoxy and the gel polymerized for 30 minutes at 4 °C. After polymerization, the chosen adhesive backed mask was placed on the coverslip. Masks were made of 0.12 mm thick adhesive backed aluminum tape (Berry Plastics, Evansville, IN) using a Cameo electronic cutting tool (Silhouette, Orem, UT). To cut the mask, the aluminum tape was placed on a cutting mat overlaid with adhesive black vinyl (U.S. Stamp & Sign, Cookeville, TN) to prevent scrunching of the aluminum during cutting.

After polymerization of the gel and addition of the mask, the reaction was initiated using a B100AP UV lamp, which has a 100-Watt bulb and a peak output at 365 nm (UVP, Upland, CA). Gels were UV exposed for 30 minutes at 4 °C. After exposure, the mask was removed and the slide with gel was incubated and covered in foil at 37 °C for 2-3 hours. After incubation the gel was imaged using a Typhoon Trio (GE Healthcare, Piscataway, NJ). Fluorescein-labeled output was imaged using 488 nm Argon ion laser excitation and 526 nm single pass emission. TYE665-labeled output was imaged using 633 nm Helium-Neon laser excitation and 670 nm band pass emission.