Table I.
Comparison Between the Experimental Data from Crystalline Ubiquitin and the Predictions Using Different Structural / MD Models
|
R factorb |
rmsd (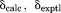 )d (ppm) )d (ppm) |
|||||||
|---|---|---|---|---|---|---|---|---|
| rmsd to 3ONSa (Å) | 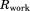 |
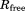 |
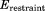 per aac (kcal/mol) per aac (kcal/mol) |
15N | 13Cα | 13Cβ |
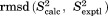 e e
|
|
| 3ONS | 0 | 0.30 | 0.31 | – | 2.39 | 0.75 | 1.11 | – |
| 1UBQ | 0.43 | 0.44 | 0.41 | – | 2.77 | 0.85 | 1.29 | – |
| 2KOX | 0.36 | 0.37 | 0.35 | – | 2.89 | 0.83 | 1.23 | 0.056 |
Solution MD,  (1 µs) (1 µs) |
0.86 | 0.41 | 0.39 | – | 3.02 | 0.97 | 1.26 | 0.048 |
Solid MD,  , 1U (1 µs) , 1U (1 µs) |
0.52 | 0.41 | 0.39 | – | 2.96 | 0.92 | 1.15 | 0.056 |
Solid MD,  , 4U (200 ns) , 4U (200 ns) |
0.37 | 0.37 | 0.35 | – | 2.91 | 0.92 | 1.12 | 0.062 |
Solid MD,  , 1U (1 µs) , 1U (1 µs) |
0.22 | 0.31 | 0.29 | 0.21 | 2.72 | 0.90 | 1.09 | 0.043 |
Solid MD,  , 4U (200 ns) , 4U (200 ns) |
0.21 | 0.32 | 0.31 | 0.18 | 2.73 | 0.90 | 1.09 | 0.040 |
Solid MD, 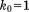 , 1U (1 µs) , 1U (1 µs) |
0.10 | 0.29 | 0.28 | 0.48 | 2.68 | 0.89 | 1.11 | 0.047 |
Solid MD, 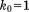 , 4U (200 ns) , 4U (200 ns) |
0.09 | 0.32 | 0.29 | 0.36 | 2.68 | 0.89 | 1.11 | 0.046 |
Solid MD, 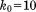 , 1U (1 µs) , 1U (1 µs) |
0.05 | 0.37 | 0.36 | 0.76 | 2.64 | 0.85 | 1.12 | 0.041 |
Solid MD, 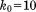 , 4U (200 ns) , 4U (200 ns) |
0.05 | 0.32 | 0.29 | 0.54 | 2.65 | 0.85 | 1.12 | 0.041 |
The shaded rows correspond to the recommended 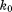 setting.
setting.
Cα rmsd relative to the crystallographic structure. In the case of crystal MD simulations, protein coordinates 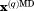 are overlaid according to Eq. (2.1) and then averaged over the entire trajectory; the average coordinates are superimposed onto 3ONS in the least-square sense (via Cα atoms) before calculating the rms deviation from
are overlaid according to Eq. (2.1) and then averaged over the entire trajectory; the average coordinates are superimposed onto 3ONS in the least-square sense (via Cα atoms) before calculating the rms deviation from 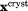 . In other cases, protein coordinates are superimposed onto 3ONS, averaged if necessary, and then used to calculate the rmsd.
. In other cases, protein coordinates are superimposed onto 3ONS, averaged if necessary, and then used to calculate the rmsd.
In calculating crystallographic R, all per-atom B factors have been omitted. This was done to facilitate the comparison between MD models (which encode local dynamics) and static structures (which are dynamics-free). Furthermore, no attempt was made to calculate reflections from explicit water molecules. In the case of crystal MD trajectories, each protein molecule was first transformed according to Eq. (2.1). Then, structure factors 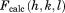 were computed using the fmodel tool in PHENIX.35 In doing so, the flat bulk-solvent contribution was included with
were computed using the fmodel tool in PHENIX.35 In doing so, the flat bulk-solvent contribution was included with 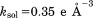 and
and 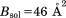 , as recommended by Fokine and Urzhumtsev.36 The obtained values
, as recommended by Fokine and Urzhumtsev.36 The obtained values 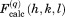 from individual ubiquitin molecules have been averaged (with phases) to determine the intensities of reflections,
from individual ubiquitin molecules have been averaged (with phases) to determine the intensities of reflections, 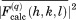 , which were in turn averaged over the entire trajectory. The result was then subjected to the overall scaling to account for the effect of lattice vibrations (translational movement of the protein molecules).37 The degree of overall anisotropy, as reported in 3ONS, is modest; therefore, we chose to use the isotropic scaling whereby a single
, which were in turn averaged over the entire trajectory. The result was then subjected to the overall scaling to account for the effect of lattice vibrations (translational movement of the protein molecules).37 The degree of overall anisotropy, as reported in 3ONS, is modest; therefore, we chose to use the isotropic scaling whereby a single 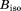 value was optimized using a designated script. Finally, the results were correlated to
value was optimized using a designated script. Finally, the results were correlated to 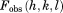 and the crystallographic R factor was calculated in a standard manner. When calculating
and the crystallographic R factor was calculated in a standard manner. When calculating 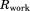 and
and 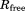 , we used the same subsets of reflections as listed for 3ONS. For structural models other than crystal MD trajectories, the protein coordinates were first superimposed onto 3ONS in the least-square sense (via Cα atoms); the remaining calculations followed the same procedure as described above.
, we used the same subsets of reflections as listed for 3ONS. For structural models other than crystal MD trajectories, the protein coordinates were first superimposed onto 3ONS in the least-square sense (via Cα atoms); the remaining calculations followed the same procedure as described above.
The restraint energy per residue, 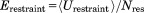 , where Urestraint is calculated according to Eq. (1) and subsequently averaged over all snapshots in the trajectory and
, where Urestraint is calculated according to Eq. (1) and subsequently averaged over all snapshots in the trajectory and 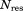 is the number of residues for which crystallographic restraints are available,
is the number of residues for which crystallographic restraints are available,  .
.
Chemical shifts were calculated using the program SHIFTX2 version 1.07.38 A customized version of the program, where ubiquitin was excluded from the training set to avoid biasing the results, was kindly provided by B. Han. The program was used on static structures as well as MD frames, processing one protein structure at a time (disregarding small shifts across protein-protein interface, e.g., due to ring current shifts). Taking intermolecular effects into consideration leads to a slight improvement in 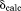 (e.g., by ca. 0.05 ppm for 15N nuclei). In the case of MD data, every 10-th snapshot was included in the chemical shift calculations, corresponding to 50-ps sampling step. The control calculations using 5-ps sampling step produced the results that were virtually identical. The experimental data were obtained from the studies by Igumenova et al.39 (13C) and Schanda et al.23 (15N); we found that there was no need to re-reference these chemical shifts.
(e.g., by ca. 0.05 ppm for 15N nuclei). In the case of MD data, every 10-th snapshot was included in the chemical shift calculations, corresponding to 50-ps sampling step. The control calculations using 5-ps sampling step produced the results that were virtually identical. The experimental data were obtained from the studies by Igumenova et al.39 (13C) and Schanda et al.23 (15N); we found that there was no need to re-reference these chemical shifts.
15N-1HN dipolar order parameters for crystal trajectories were computed using the following protocol. First, symmetry transformations Eq. (2.1) have been applied to all ubiquitin molecules in the periodic boundary box. Then, 15N-1HN vectors were extracted from the transformed coordinates; the vectors pertaining to each individual residue were arranged in a long array. The array had an effective length of 6 × 1 = 6 µs in the case of 1U simulations and 0.2 × 24 = 4.8 µs in the case of 4U simulations. Finally, the standard Brüschweiler's formula40 has been applied to these arrays to calculate 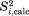 values. The experimental data
values. The experimental data 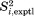 are from the recent solid-state NMR experiments by Haller and Schanda,41 which is the revision of the earlier work by Schanda et al.23 Additionally, the table includes the results from solution-state ensemble 2KOX and 1 µs-long solution simulation. For these models,
are from the recent solid-state NMR experiments by Haller and Schanda,41 which is the revision of the earlier work by Schanda et al.23 Additionally, the table includes the results from solution-state ensemble 2KOX and 1 µs-long solution simulation. For these models, 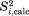 values were obtained by straightforward application of the Brüschweiler's formula.
values were obtained by straightforward application of the Brüschweiler's formula.
