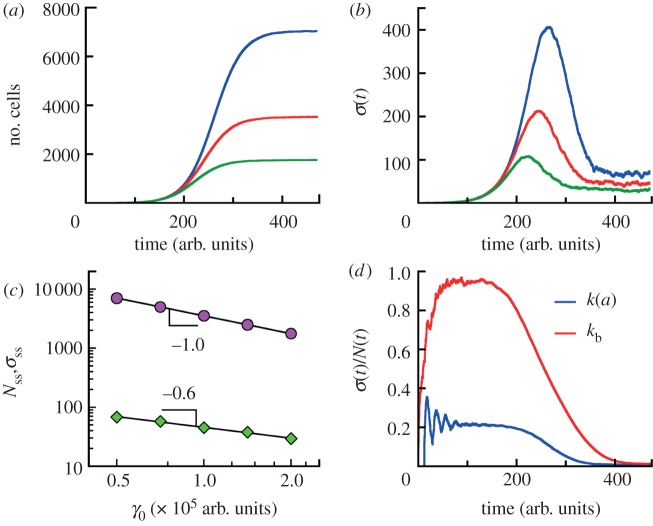
Figure 7.

Competitive growth. (a) The average numbers of cells as functions of time for competitive populations with age-dependent cell division rate k(a) (distribution II, see caption to figure 1d) and death rates proportional to the number of other individuals γ = γ₀(n − 1). The populations are grown from a single cell of the zero age a = 0. The numbers of cells reach the steady state N_ss at long times. The data for each γ₀ are obtained from simulations for 120 growth trajectories. (b) The standard deviations σ(t) of the mean sizes of competitive populations from data in (a) are non-monotonic functions of time. At long times, σ(t) approach the limiting values σ_ss in contrast to exponentially growing populations. The population size distributions at steady state are stationary Gaussian around mean sizes N_ss (see the electronic supplementary material, figure S9 of SI). (c) The average numbers of cell N_ss (circles) and its standard deviations σ_ss (diamonds) at steady state are shown as a function of ‘competitive’ cell death rate γ₀. The data are analysed in the time interval from t = 400 arb. units to t = 474 arb. units for all values of γ₀. The mean population is inversely proportional to γ₀. (d) Comparison of the population fluctuation for age-dependent (blue) and age-independent (constant division rate k_b) (red) models. γ₀ for these models are identical. Parameters are chosen so that the average growth rates in the absence of cell death are identical. The age-dependent model shows a significantly different behaviour.