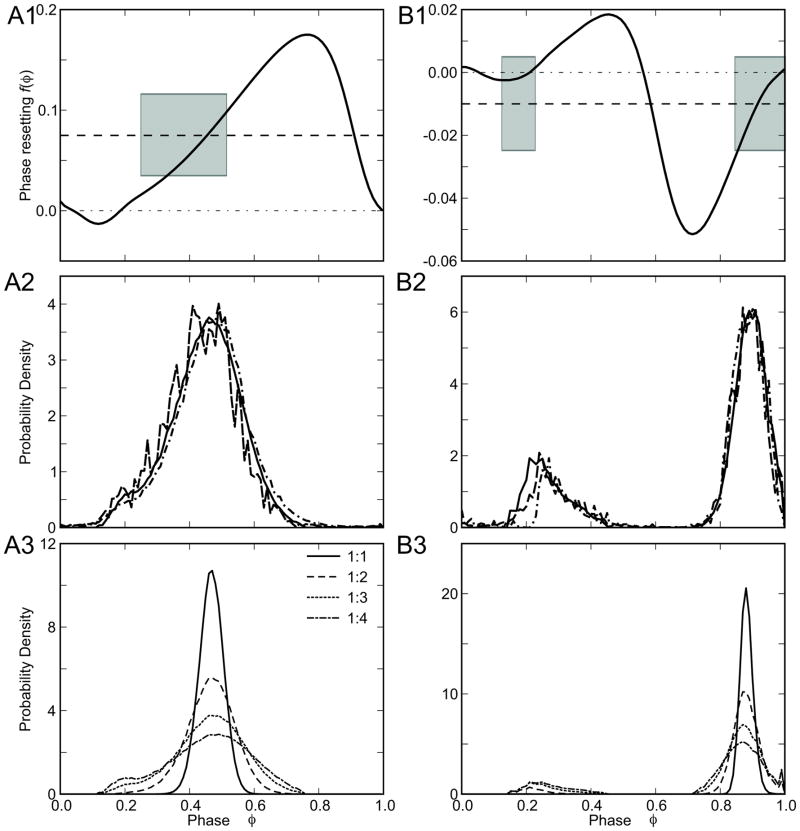
Figure 1.

Comparison of theoretical and simulated probability density functions for populations of oscillators with a Gaussian distribution in the intrinsic period. A. Type 1 Morris-Lecar model, A1) PRC for single neuron, A2) Phase probability density functions for heterogeneous population. Theoretical prediction (solid curve), and simulations of phase oscillators (dotted curve) were obtained for μ_i= 76.5 ms, σ_i=1.0, P_F=235.62 ms and N=3. The inverse F-I curve was used to select the values of applied currents for conductance-based simulations (dashed line) in order to satisfy a normal distribution with the nominal mean and standard deviation in period. A3) The theoretical prediction of the phase probability density obtained from Eq. 11 for different values of N. B. Type 2 Morris-Lecar model, B1) PRC for single neuron, B2) Phase probability density functions for heterogeneous population with μ_i =82.21ms σ_i=0.4, P_F=242.82 ms and N=3. The thick dashed horizontal line in A1 and B1 corresponds to deterministic value of f(φ^*) with mean period μ computed using Eq. 9. Shaded regions indicate the deterministic solutions on a stable branch as the period varies plus or minus a standard deviation μ_i ± σ_i. C. Dependence of the tightness of phase locking on N, the number of intrinsic cycles that elapse between forcing inputs. B3) Same as A3, but for Type 2 model.