Figure 1.

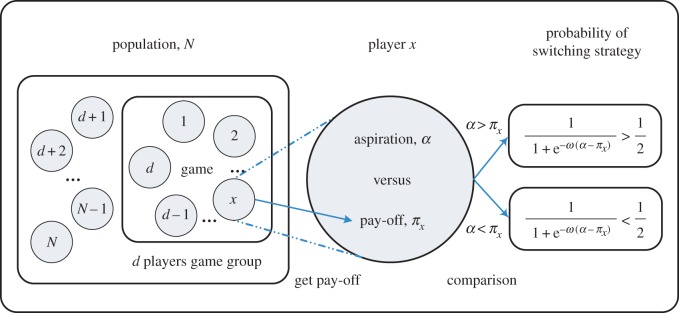
Evolutionary game dynamics of d-player interactions driven by global aspiration. In our mathematical model of human strategy updating driven by self-learning, a group of d players is chosen randomly from the finite population to play the game. According to this, game players calculate and obtain their actual pay-offs. They are more likely to stochastically switch strategies if the pay-offs they aspire are not met. On the other hand, the higher the pay-offs are compared with the aspiration level α, the less likely they switch their strategies. Besides, strategy switching is also determined by a selection intensity ω. For vanishing selection intensity, switching is entirely random irrespective of pay-offs and the aspiration level. For increasing selection intensity, the self-learning process becomes increasingly more ‘optimal’ in the sense that for high ω, individuals tend to always switch when they are dissatisfied, and never switch when they are tolerant. We examine the simplest possible set-up, where the level of aspired pay-off α is a global parameter that does not change with the dynamics. We show, however, that statements about the average abundance of a strategy do not depend on α under weak selection 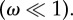(Online version in colour.)