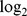Abstract
Extrinsic and intrinsic regulators are responsible for the tight control of hematopoietic stem cells (HSCs), which differentiate into all blood cell lineages. To understand the fundamental basis of HSC biology, we focused on differentially expressed genes (DEGs) in long-term and short-term HSCs, which are closely related in terms of cell development but substantially differ in their stem cell capacity. To analyze the transcriptional regulation of the DEGs identified in the novel transcriptome profiles obtained by our RNA-seq analysis, we developed a computational method to model the linear relationship between gene expression and the features of putative regulatory elements. The transcriptional regulation modes characterized here suggest the importance of transcription factors (TFs) that are expressed at steady state or at low levels. Remarkably, we found that 24 differentially expressed TFs targeting 21 putative TF-binding sites contributed significantly to transcriptional regulation. These TFs tended to be modulated by other nondifferentially expressed TFs, suggesting that HSCs can achieve flexible and rapid responses via the control of nondifferentially expressed TFs through a highly complex regulatory network. Our novel transcriptome profiles and new method are powerful tools for studying the mechanistic basis of cell fate decisions.
Introduction
Hematopoiesis is a complex and dynamic process, which generates mature blood cells throughout the life of organisms. In the adult bone marrow, long-term hematopoietic stem cells (LT-HSCs) maintain a balanced pool of stem cells, which also differentiates into more mature short-term hematopoietic stem cells (ST-HSCs), multipotent progenitors with a lower self-renewal capacity. It is believed that the blood lineage choice of HSCs is governed by a stepwise cell fate decision [1], [2]. However, recent studies have raised questions about the hierarchical hematopoietic system [3], [4]. Many studies based on genome-wide gene expression profiling [5]–[9] have demonstrated that specific extrinsic and intrinsic regulators play key roles in hematopoiesis [10]–[12]. Recently, high-throughput sequencing techniques have been applied widely [13]–[15], which have provided new insights into in vivo transcription factor (TF) binding and epigenetic modifications [16]–[18]. Systems biology approaches are also enhancing our understanding of the regulatory dynamics of hematopoiesis [19].
Despite the biological importance of the formation of all blood cells via a transition from LT-HSC to ST-HSC, little is known about the mechanism that underlies this early differentiation. A major explanation for this deficiency is a lack of comprehensive genome-wide identification studies and characterizations of the regulatory elements that govern gene expression in HSCs. The profiling of potential key regulators [8], [17], [20] and the large-scale integration of datasets [21], [22] have improved our understanding greatly. However, these studies are limited to a small number of factors that function in heterogeneous HSCs, which were isolated using different combinations of monoclonal antibodies. Therefore, unconsidered key regulators may exist at this early stage of hematopoiesis. Indeed, novel key factors [23], [24] and new multipotent progenitors [3], [4], [25] have been identified recently.
To address these deficiencies, we developed a computational method on the basis of novel transcriptome data from adult mouse bone marrow HSCs;  (c-kit+Sca1+Lin−) LT-HSCs and
(c-kit+Sca1+Lin−) LT-HSCs and 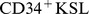 ST-HSCs, a widely used strategy to isolate HSCs at high purity [26], [27]. Our method uses a regression-based approach [28]–[30] to model the linear relationships between gene expression and the characteristics of regulatory elements compiled from a database. In the present study, we extended this regression modeling-based approach using large-scale log-linear modeling (LLM) [31], which considered the combinatorial nature of TFs. Thus, our method can systematically infer the regulation modes exerted by TFs that are probably necessary for gene expression, as well as suggesting synergistic TF modules. Using our transcriptome profiles and this novel method, we characterized transcriptional regulatory modes related to HSCs, which suggested the functional importance of TFs expressed at steady-state or low levels. Remarkably, we identified 24 differentially expressed TFs that targeted 21 putative TF-binding sites (TFBSs) in LT-HSCs. These TFs might be essential for maintaining the HSC capacity during the early stage of hematopoiesis.
ST-HSCs, a widely used strategy to isolate HSCs at high purity [26], [27]. Our method uses a regression-based approach [28]–[30] to model the linear relationships between gene expression and the characteristics of regulatory elements compiled from a database. In the present study, we extended this regression modeling-based approach using large-scale log-linear modeling (LLM) [31], which considered the combinatorial nature of TFs. Thus, our method can systematically infer the regulation modes exerted by TFs that are probably necessary for gene expression, as well as suggesting synergistic TF modules. Using our transcriptome profiles and this novel method, we characterized transcriptional regulatory modes related to HSCs, which suggested the functional importance of TFs expressed at steady-state or low levels. Remarkably, we identified 24 differentially expressed TFs that targeted 21 putative TF-binding sites (TFBSs) in LT-HSCs. These TFs might be essential for maintaining the HSC capacity during the early stage of hematopoiesis.
Results
Extensive transcriptome discovery
RNA-seq analysis of HSCs
To establish transcriptional profiles, we extracted total RNA from mouse LT-HSCs (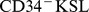 ) and ST-HSCs (
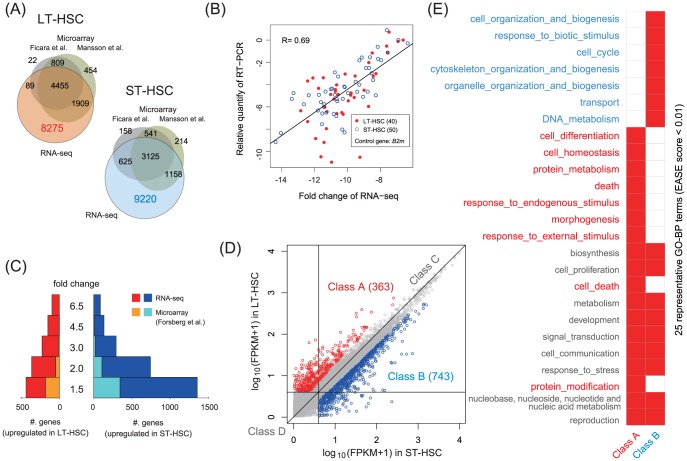
) and ST-HSCs (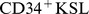 ), and performed SOLiD RNA-seq assays in triplicate. We generated 44–70 million 50 bp short reads, among which 44%–63% were mapped uniquely to the mouse genome (mm9) via our recursive mapping strategy [32]. These uniquely mapped reads (uni-reads) were used for further analysis (Table S1). We used the TopHat/Cufflinks pipeline [33] to quantify the RNA abundance of RefSeq genes as fragments per kilobase of exon per million mapped reads (FPKM). This analysis confirmed the high reproducibility among replicates (Figure S1A). We also assessed the overlap between our profile and public expression profiles [8], [9]. This comparison showed that our RNA-seq assay uniquely identified 8275 and 9220 genes from LT- and ST-HSCs, respectively (Figure 1A). This indicates that our study successfully identified a more detailed transcriptome landscape than previous studies.
), and performed SOLiD RNA-seq assays in triplicate. We generated 44–70 million 50 bp short reads, among which 44%–63% were mapped uniquely to the mouse genome (mm9) via our recursive mapping strategy [32]. These uniquely mapped reads (uni-reads) were used for further analysis (Table S1). We used the TopHat/Cufflinks pipeline [33] to quantify the RNA abundance of RefSeq genes as fragments per kilobase of exon per million mapped reads (FPKM). This analysis confirmed the high reproducibility among replicates (Figure S1A). We also assessed the overlap between our profile and public expression profiles [8], [9]. This comparison showed that our RNA-seq assay uniquely identified 8275 and 9220 genes from LT- and ST-HSCs, respectively (Figure 1A). This indicates that our study successfully identified a more detailed transcriptome landscape than previous studies.
Figure 1. Extensive transcriptome discovery based on the RNA-seq assay.
(A) Our RNA-seq assay discovered over 8200 mRNAs that were not detected in microarray-based studies. (B) RNA quantities relative to those of the housekeeping gene beta-2 microglobulin (B2m) were correlated in qRT-PCR and RNA-seq assays, but variations were also observed in genes that were expressed at low levels. (C) Analysis of gene expression changes detected a transcriptionally active state in ST-HSCs with a larger number of genes than those considered previously. (D) We categorized genes into 4 classes; Class A and Class B, in which FC 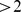 and FPKM
and FPKM 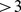 , Class C (6332 genes), in which FC
, Class C (6332 genes), in which FC 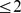 and FPKM
and FPKM 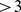 , and Class D (6006 genes), in which FPKM
, and Class D (6006 genes), in which FPKM 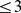 . Class A and Class B represented DEGs, Class C represented steady-state transcription genes, and Class D represented genes with noisy expression and/or functional low-expression genes. (E) Enriched GO biological process (GO-BP) terms detected by DAVID (EASE score,
. Class A and Class B represented DEGs, Class C represented steady-state transcription genes, and Class D represented genes with noisy expression and/or functional low-expression genes. (E) Enriched GO biological process (GO-BP) terms detected by DAVID (EASE score, 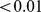 , complete lists in Tables S10 and S11).
, complete lists in Tables S10 and S11).
The application of different monoclonal antibodies to purify HSC populations may have diverse effects on the resulting expression profiles [2], which are related to issues regarding the functional purification of HSCs [10], [26] and the heterogeneous expression in single cells [4], [10], [34]. In fact, a comparison between our findings and the results of an RNA-seq analysis of HSCs isolated using distinct markers [15] demonstrated that there were great differences, particularly among genes that were expressed at low levels (Figure S1B). In addition, we performed qRT-PCR using 90 genes that were randomly selected from our samples, and confirmed that RNA quantities relative to the housekeeping gene B2m were in overall agreement (Figure 1B). However, genes that were expressed at low levels were substantially different. These results suggest the difficulty in detecting and quantifying rare transcripts in HSCs.
Identification of differentially expressed genes (DEGs)
We identified genes with high expression levels (FPKM, 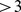 ) and calculated the fold change (FC) in gene expression. This analysis detected the transcriptionally active state of ST-HSCs (Figure 1C), which supported the results of previous studies [6], [7], [15]. Our RNA-seq assay detected a higher number of DEGs than those reported previously, which may have been related to our more comprehensive transcriptome discovery method. We categorized the genes into 4 classes using a change of 2-fold as the threshold [15] (Figure 1D): Class A, 363 genes upregulated in LT-HSC; Class B, 743 genes downregulated in LT-HSC; Class C, 6332 genes with FC
) and calculated the fold change (FC) in gene expression. This analysis detected the transcriptionally active state of ST-HSCs (Figure 1C), which supported the results of previous studies [6], [7], [15]. Our RNA-seq assay detected a higher number of DEGs than those reported previously, which may have been related to our more comprehensive transcriptome discovery method. We categorized the genes into 4 classes using a change of 2-fold as the threshold [15] (Figure 1D): Class A, 363 genes upregulated in LT-HSC; Class B, 743 genes downregulated in LT-HSC; Class C, 6332 genes with FC 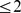 and FPKM
and FPKM 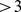 ; and Class D, 6006 genes with low expression (FPKM,
; and Class D, 6006 genes with low expression (FPKM, 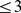 ). Thus, Class A and Class B represented DEGs, Class C represented steady-state transcription genes, and Class D represented genes with noisy expression and/or functional low expression genes.
). Thus, Class A and Class B represented DEGs, Class C represented steady-state transcription genes, and Class D represented genes with noisy expression and/or functional low expression genes.
We searched for any gene ontology (GO) terms enriched in DEGs using the DAVID Bioinformatics Resources [35]. Figure 1E shows the representative GO terms (Tables S10 and S11 for complete lists). This analysis showed that DEGs were involved in the immune response, cell–cell communication, and signal transduction. This was not surprising because extrinsic and intrinsic signals and molecules contribute to the biology of HSCs in the bone marrow microenvironment [1], [10], [11], [36]. In addition to these common biological processes, Class A genes were involved particularly in cell death, cell differentiation, and homeostasis, whereas Class B genes were involved in DNA repair, cell cycle progression, and cell organization. These results were consistent with those of previous studies that showed that apoptosis and cell-cycle regulators play critical roles in maintaining a balanced pool of HSCs and in the expansion of progenitor populations [5], [37], [38].
Differentially expressed cell-surface molecules and TFs
DEGs included 77 cell-surface molecules with the ''cell surface'' (GO:0009986) GO term (Table S2), some of which are known to be associated with hematopoiesis: in Class A, Vwf, Lhcgr, Cxcl12, and Tgfbr3; in Class B, CD244, CD33, and Clec12a. CD34, which was used to isolate HSCs in this study, exhibited an upregulation of over 12-fold in ST-HSCs compared with LT-HSCs. To obtain high HSC purities, these cell-surface molecules will be useful as alternative or additional markers.
DEGs also included 57 TFs that were annotated in TRANSFAC [39], i.e., 31 in Class A and 26 in Class B (Tables 1 and S3). These differentially expressed TFs included known hematopoietic regulators (e.g., Gata2, Tal1, and Satb1) and previously unconsidered TFs, such as the hepatocyte nuclear factor Foxa3, the BTB-domain zinc finger Zbtb20, the DNA-binding domain Arid5a, and the epigenetic regulator Uhrf1. It was noteworthy that a large number of TFs belonged to Class C (303 TFs) and Class D (341 TFs) (Tables S4 and S5). In particular, TFs with synergistic functions in HSCs [17] and that belonged to TF families, such as Fox, Lmo, and Sox (which are required by HSCs), were present in Class C and/or Class D. These results may suggest that, in addition to differentially expressed TFs, TFs with coding genes that are expressed at stable or low levels are functionally important molecules.
Table 1. Top ten differentially expressed transcription factors.
| Class | Gene | FC* | Microarray† | Description |
| A | Rorc | 6.4252 | RAR-related orphan receptor gamma | |
| Hoxb5 | 5.1317 | homeobox B5 | ||
| Rarb | 3.8601 | retinoic acid receptor, beta | ||
| Cdkn1c | 3.8479 | M,Fo | cyclin-dependent kinase inhibitor 1C (P57) | |
| Fosb | 3.0942 | Fi,M | FBJ osteosarcoma oncogene B | |
| Car1 | 2.9839 | M | carbonic anhydrase 1 | |
| Id1 | 2.9708 | inhibitor of DNA binding 1 | ||
| Klf1 | 2.8796 | M | Kruppel-like factor 1 (erythroid) | |
| Nr4a1 | 2.7957 | Fi,M | nuclear receptor subfamily 4, group A, member 1 | |
| Foxa3 | 2.7509 | forkhead box A3 | ||
| B | Satb1 | 3.7749 | Fi,M,Fo | special AT-rich sequence binding protein 1 |
| Hnf4a | 3.1733 | hepatic nuclear factor 4, alpha | ||
| Trf | 2.5921 | transferrin | ||
| Hmgb2 | 2.0842 | M | high mobility group box 2 | |
| Runx3 | 1.9827 | runt related transcription factor 3 | ||
| Irf8 | 1.8349 | interferon regulatory factor 8 | ||
| Arid5a | 1.7884 | AT rich interactive domain 5A (MRF1-like) | ||
| Uhrf1 | 1.4536 | ubiquitin-like, containing PHD and RING finger domains, 1 | ||
| Zfp422 | 1.4477 | Fi,M | zinc finger protein 422 | |
| Notch1 | 1.3403 | notch 1 |
Computational modeling of DEG promoters
Workflow overview of promoter modeling
To determine the upstream regulatory elements that are essential for DEG transcription, we used a linear regression model that was used widely for this purpose in previous studies [28], [30]. The underlying assumption of this model is that the expression levels of genes are controlled by the sum of the independent activities of regulators, such as DNA-binding factors or epigenetic marks. These activities can be approximated using high-throughput in vivo experiments [40], [41] or knowledge-based computational approaches [25], [30]. As a preliminary test, we applied the linear regression model described in our previous study [29] using ChIP-seq data for 10 major TFs [17]. In this approach, we used genome-wide TF-binding instances that occurred within 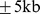 regions from transcription start sites (TSSs), and predicted the FPKMs of DEGs by using a simple linear regression model with rigorous statistical tests. However, we were unable to detect any significant effects, and the correlation between the observed and predicted FPKMs was
regions from transcription start sites (TSSs), and predicted the FPKMs of DEGs by using a simple linear regression model with rigorous statistical tests. However, we were unable to detect any significant effects, and the correlation between the observed and predicted FPKMs was 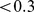 . This failure may, in part, reflect the possibility that these TFs exert regulatory functions as distal enhancers, rather than through proximal promoters [17], [42].
. This failure may, in part, reflect the possibility that these TFs exert regulatory functions as distal enhancers, rather than through proximal promoters [17], [42].
To identify regulators from proximal promoter regions comprehensively, we used TRANSFAC [39], which is a database that curates 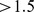 million ChIP-seq sites, and designed a workflow coupled with intensive computations (Figure 2). First, we prepared the promoter sequences of DEGs and searched for putative TFBSs and mouse TFs that are known to bind to the TFBSs in TRANSFAC using the MATCH tool [43]. This procedure identified 140 and 141 TFBSs for Class A and Class B promoters, respectively. Among these, 70 TFBSs in Class A and 69 TFBSs in Class B were targeted by at least one TF with a highly expressed coding gene (FPKM,
million ChIP-seq sites, and designed a workflow coupled with intensive computations (Figure 2). First, we prepared the promoter sequences of DEGs and searched for putative TFBSs and mouse TFs that are known to bind to the TFBSs in TRANSFAC using the MATCH tool [43]. This procedure identified 140 and 141 TFBSs for Class A and Class B promoters, respectively. Among these, 70 TFBSs in Class A and 69 TFBSs in Class B were targeted by at least one TF with a highly expressed coding gene (FPKM, 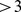 ). In total, 265 and 267 TFs were involved in Class A and Class B, respectively.
). In total, 265 and 267 TFs were involved in Class A and Class B, respectively.
Figure 2. Overview of computational promoter modeling.
We searched putative TFBSs and mouse TFs from 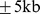 DNA sequences of TSSs, and used these for inferring TF–TF interaction probability and calculating TGASs. We searched the best combination of TFBSs represented by TGASs to predict FPKMs of a gene class in LT- or ST-HSCs by performing 5-fold CVs iteratively.
DNA sequences of TSSs, and used these for inferring TF–TF interaction probability and calculating TGASs. We searched the best combination of TFBSs represented by TGASs to predict FPKMs of a gene class in LT- or ST-HSCs by performing 5-fold CVs iteratively.
Next, we calculated the TFBS–gene association score (TGAS) using 5 distinct scoring schemes, which were employed as explanatory variables in a linear regression model. These scores considered matrix similarity, positional bias of TFBSs, the expression levels of TFs, and the probability of TF–TF interactions (Materials and Methods). Given a TGAS, we searched exhaustively for the best combination of TFBSs, including pairwise interactions between TFBSs. We performed a 5-fold cross-validation (CV) to avoid the risk of over-fitting. This procedure was repeated 100 times with different random seeds. An ensemble of 100 regression coefficients (RCs) for a TFBS provides statistical information of the estimated regulatory activity of the TFBS. We conducted statistical tests using these ensembles. We applied this workflow to 4 regression models to predict the expression levels of each of the Class A and Class B genes in LT- or ST-HSCs.
We attempted to characterize promoter architectures by testing the different TGASs mentioned above, rather than by comparing our approach with other modeling methods. This was because of the difficulty of implementing existing methods using our inputs and analyzing their results. We also aimed to determine regulatory activities by analyzing 4 models. We characterized the context-dependent function of regulators that activated and repressed the transcription of distinct genes depending on the cellular context [44], [45]. Thus, our approach provided a detailed picture of the regulatory modes involved in context-dependent gene expression.
Inference of higher-order TF interactions
The co-occupancy of a promoter by multiple TFs contributes synergistically to transcriptional regulation. We considered this when calculating TGAS by performing probabilistic LLM [31] coupled with iterative random sampling. The input matrix used for LLM, i.e., n promoters in rows 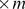 TFs in columns, comprised binary values that represent the existence of TFBSs for m TFs in n promoters. Using this matrix, LLM was employed to infer the conditional (in)dependency of TF occurrences, i.e., TF–TF interactions in higher-order conditional distributions. It should be noted that LLM cannot determine whether an interaction is competitive or cooperative.
TFs in columns, comprised binary values that represent the existence of TFBSs for m TFs in n promoters. Using this matrix, LLM was employed to infer the conditional (in)dependency of TF occurrences, i.e., TF–TF interactions in higher-order conditional distributions. It should be noted that LLM cannot determine whether an interaction is competitive or cooperative.
The huge number of TFs means that LLM is not adequate to compute them all; therefore, we performed random sampling with 10 arbitrary selected TFs, which means that an inferred TF–TF interaction was observed constantly in the 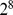 state combinations of 8 TFs. This sampling procedure was terminated if an outcome had no effect during
state combinations of 8 TFs. This sampling procedure was terminated if an outcome had no effect during 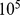 runs. We calculated the interaction probability Pr for all possible TF pairs using this iterative sampling procedure (Materials and Methods). After repeating the sampling procedure 1,367,639 times for Class A and 1,406,837 times for Class B, we retrieved 50 and 77 interactions (
runs. We calculated the interaction probability Pr for all possible TF pairs using this iterative sampling procedure (Materials and Methods). After repeating the sampling procedure 1,367,639 times for Class A and 1,406,837 times for Class B, we retrieved 50 and 77 interactions (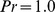 ) from Class A and Class B, respectively (Tables S12 and S13).
) from Class A and Class B, respectively (Tables S12 and S13).
Performance of regression models
Overall, Pearson's correlation coefficient Rs in learning and testing of 5-fold CVs showed a slight over-fitting in the range of 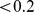 (Figure S5), which was acceptable in our sense. One of the reasons for this over-fitting was the unbalanced numbers between testing genes and TFBSs; e.g., 72 Class A genes (a subset of 5-fold CV) were tested by a model with over 100 predictors that were trained by the remaining Class A genes. This implies that the constructing of a model to generalize the gene regulation for an HSC population is a highly difficult challenge that is associated with the degrees of functional purity and heterogeneity and the limit of regulatory features used in the modeling.
(Figure S5), which was acceptable in our sense. One of the reasons for this over-fitting was the unbalanced numbers between testing genes and TFBSs; e.g., 72 Class A genes (a subset of 5-fold CV) were tested by a model with over 100 predictors that were trained by the remaining Class A genes. This implies that the constructing of a model to generalize the gene regulation for an HSC population is a highly difficult challenge that is associated with the degrees of functional purity and heterogeneity and the limit of regulatory features used in the modeling.
Table 2 summarizes the results obtained from the linear regression models. The results showed that TGAS V coupled with LLM had the highest mean R between the observed and predicted gene expression. Interestingly, TGAS IV, which removed TFBSs where all TFs had FPKM 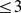 , yielded poor–quality models, suggesting that these TFBSs were also necessary for modeling gene regulation. In addition, compared with the main effect terms (denoted as ''single'' in Table 2), a large number of pairwise terms, i.e.,
, yielded poor–quality models, suggesting that these TFBSs were also necessary for modeling gene regulation. In addition, compared with the main effect terms (denoted as ''single'' in Table 2), a large number of pairwise terms, i.e., 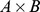 , where A and B are 2 distinct TFBSs that were not included as main effect terms, contributed to the modeling. Indeed, the initial models that comprised only the main effect terms selected on the basis of Akaike's information criterion (AIC) showed an R
, where A and B are 2 distinct TFBSs that were not included as main effect terms, contributed to the modeling. Indeed, the initial models that comprised only the main effect terms selected on the basis of Akaike's information criterion (AIC) showed an R
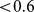 .
.
Table 2. Result obtained using the linear regression models.
| Linear regression | TFBS contents | |||||
| Class | Cell | TGAS* | TFBSs | R† | Single | Pairwise |
| A | LT-HSC | I | 83.91 (5.7238)§ | 0.8016 (0.0205) | 18.98 (2.1070) | 64.93 (5.7745) |
| II | 98.69 (5.5492) | 0.8482 (0.0197) | 30.67 (2.6685) | 68.02 (5.8378) | ||
| III | 103.73 (4.5296) | 0.8722 (0.0134) | 29.14 (2.5220) | 74.59 (5.0062) | ||
| IV | 47.28 (2.9260) | 0.6771 (0.0165) | 11.15 (1.2835) | 36.13 (2.9888) | ||
| V | 108.12 (4.9138) | 0.8850 (0.0124) | 31.82 (2.6921) | 76.30 (5.1449) | ||
| V-1 | 84.42 (4.0748) | 0.8334 (0.0154) | 18.59 (6.3594) | 65.83 (7.0129) | ||
| V-2 | 51.90 (2.9648) | 0.7164 (0.0155) | 11.96 (1.1128) | 39.94 (3.0588) | ||
| V-3 | 91.38 (4.3053) | 0.8284 (0.0146) | 28.01 (2.5120) | 63.37 (4.8634) | ||
| ST-HSC | I | 83.02 (5.3907) | 0.8087 (0.0204) | 20.66 (1.9709) | 62.36 (5.9389) | |
| II | 101.65 (4.7188) | 0.8463 (0.0180) | 37.47 (2.8088) | 64.18 (5.6416) | ||
| III | 106.77 (4.0394) | 0.8730 (0.0114) | 36.29 (2.7579) | 70.48 (4.5902) | ||
| IV | 50.34 (3.1376) | 0.6786 (0.0215) | 17.63 (2.0768) | 32.71 (3.6064) | ||
| V | 108.49 (4.5618) | 0.8777 (0.0132) | 37.62 (2.7378) | 70.87 (5.2548) | ||
| V-1 | 85.01 (4.2883) | 0.8289 (0.0160) | 22.75 (2.1372) | 62.26 (4.3327) | ||
| V-2 | 53.32 (3.1012) | 0.6867 (0.0191) | 21.53 (2.2470) | 31.79 (3.5222) | ||
| V-3 | 86.71 (4.8853) | 0.8126 (0.0196) | 26.03 (2.6399) | 60.68 (5.4934) | ||
| B | LT-HSC | I | 77.82 (5.6451) | 0.6177 (0.0183) | 21.98 (2.1400) | 55.84 (6.2749) |
| II | 100.86 (4.3244) | 0.7016 (0.0147) | 30.33 (2.8002) | 70.53 (4.9748) | ||
| III | 105.78 (3.8251) | 0.7311 (0.0125) | 27.96 (2.4614) | 77.82 (4.1434) | ||
| IV | 49.50 (2.8231) | 0.5410 (0.0143) | 15.29 (1.7164) | 34.21 (3.1058) | ||
| V | 108.45 (4.2270) | 0.7466 (0.0111) | 27.20 (2.4819) | 81.25 (4.3183) | ||
| V-1 | 87.86 (3.7895) | 0.6736 (0.0159) | 28.59 (3.1051) | 59.27 (4.9272) | ||
| V-2 | 53.74 (2.7879) | 0.5548 (0.0145) | 15.54 (1.5324) | 38.20 (3.1969) | ||
| V-3 | 84.45 (3.8350) | 0.6662 (0.0149) | 24.95 (2.5744) | 59.50 (4.6573) | ||
| ST-HSC | I | 77.65 (4.7924) | 0.6077 (0.0175) | 21.42 (2.0745) | 56.23 (5.3514) | |
| II | 100.69 (5.3846) | 0.6980 (0.0169) | 25.74 (2.4602) | 74.95 (6.0056) | ||
| III | 105.87 (4.1633) | 0.7262 (0.0140) | 24.73 (2.4448) | 81.14 (4.8477) | ||
| IV | 50.07 (2.8679) | 0.5160 (0.0161) | 14.36 (1.7235) | 35.71 (3.3920) | ||
| V | 107.32 (4.4763) | 0.7325 (0.0135) | 24.77 (2.6338) | 82.55 (4.6720) | ||
| V-1 | 86.98 (3.8781) | 0.6716 (0.0166) | 22.62 (2.4891) | 64.36 (4.6206) | ||
| V-2 | 54.09 (2.9397) | 0.5354 (0.0164) | 15.65 (1.8993) | 38.44 (3.5080) | ||
| V-3 | 84.96 (4.1639) | 0.6544 (0.0165) | 21.47 (2.4185) | 63.49 (4.9830) | ||
E.g., at the top line, the final regression model predicted Class A FPKMs in LT-HSCs using TGAS I, resulting in the correlation coefficient 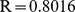 . This model included 83.91 TFBSs consisting of 18.98 single TFBSs and 64.93 pairwise TFBSs.
. This model included 83.91 TFBSs consisting of 18.98 single TFBSs and 64.93 pairwise TFBSs.
*TFBS-Gene association scores; (I) MATCH score only, (II) including distribution of TFBSs, (III) including expression changes in TFs, (IV) same as (III) but only including TFBSs targeted by highly expressed TFs, and (V) including the TF–TF interactions in the log-linear model. (V) was modified to remove TFs: coded by undetectable transcripts (V-1), those that belonged to Class D (V-2), or by removing the 21 TFBSs in Figure 4B (V-3).
Pearson's correlation coefficient; once the final regression model was found, R reflecting the model quality is calculated to measure the degree of correlation between the observed and predicted FPKMs.
Data are presented as the means (and standard deviation in parentheses).
The improvement observed using TGAS V compared with the use of TGAS III was not remarkable. To assess this improvement, we performed a two-sample t-test using RC ensembles of TFBSs that were common in the 2 models. This analysis indicated that these models yielded considerably different TFBS activities (Figure S2A). In most cases, TF interaction scores (Equation 9) were ineffectively small. However, specific TFBSs, such as AP-1, Ets, and Ebox, had high scores (Figure S2B) because of the relatively larger number of TFs that interacted to occupy these TFBSs (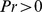 ). This apparently affected the different estimations.
). This apparently affected the different estimations.
Overall, pairwise interactions between TFBSs reflected regulatory modules that appeared to be essential components of the transcriptional machinery. The incorporation of cooperative and competitive interactions among TFs into quantitative models is also essential for determining the transcriptional network based on a fine-tuned explanation of gene expression.
Propensity of inferred TFBS activities
Identification of significant TFBSs and changes of regulatory activities
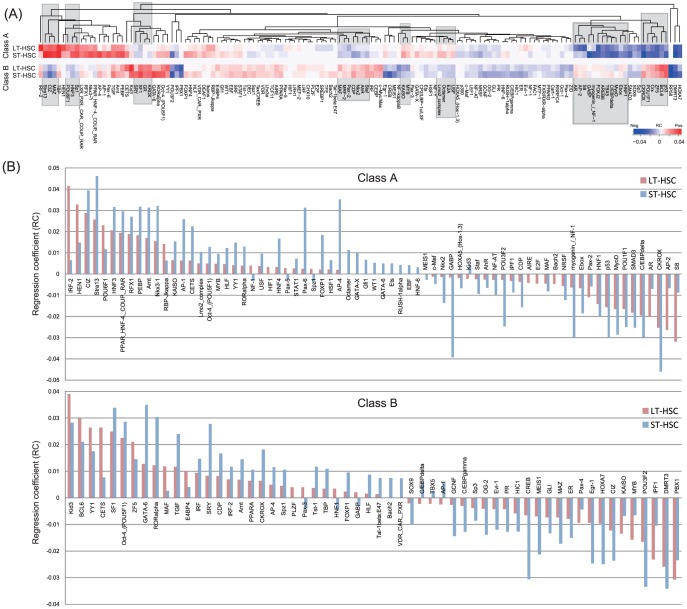
To assess the statistical significance of TFBS activities, we performed single-sample t-tests using RC ensembles on the basis of TGAS V (Figure S3). This analysis identified 142 TFBSs that rejected the null hypothesis that the mean value of RCs was equal to zero (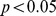 ). This included several known hematopoietic regulators, such as Arnt, C/EBP, CREB, Ebox, Egr-1, GATA-X, and IRF (Figure 3A). In particular, GATA-X targeted by Gata1, Gata2, or Gata3 (Class A) was significant only in the model of Class A in ST-HSCs. Consistent with a recent analysis of Hlf function [25], we inferred positive RCs for HLF in all 4 models, which suggests that it functions as an activator. Hlf was upregulated by 1.9-fold in LT-HSCs (Class C). We also validated PPARG activity using a competitive repopulating assay (see below).
). This included several known hematopoietic regulators, such as Arnt, C/EBP, CREB, Ebox, Egr-1, GATA-X, and IRF (Figure 3A). In particular, GATA-X targeted by Gata1, Gata2, or Gata3 (Class A) was significant only in the model of Class A in ST-HSCs. Consistent with a recent analysis of Hlf function [25], we inferred positive RCs for HLF in all 4 models, which suggests that it functions as an activator. Hlf was upregulated by 1.9-fold in LT-HSCs (Class C). We also validated PPARG activity using a competitive repopulating assay (see below).
Figure 3. Propensity of significant TFBS activities.
(A) Heat map showing regression coefficients (RCs) of 142 potentially important TFBSs (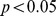 ). Rectangles indicate typical cases of opposing RCs in Class A and Class B. (B) We found that 71 and 58 TFBSs from Class A and Class B promoters, respectively, had significantly different RCs in LT- and ST-HSCs (
). Rectangles indicate typical cases of opposing RCs in Class A and Class B. (B) We found that 71 and 58 TFBSs from Class A and Class B promoters, respectively, had significantly different RCs in LT- and ST-HSCs (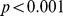 ).
).
Overall, 83 of the 142 TFBSs were detected by all 4 models, among which 14 TFBSs were unique in Class A or Class B (Table S6). Furthermore, 73% (61/83) of the common TFBSs appeared to have same effects on the activities in LT- and ST-HSCs, e.g., a positive RC in LT-HSC was also positive in ST-HSC. Interestingly, this effect was the opposite in Class A and Class B, for which typical examples are marked by rectangles in Figure 3A. There were also exceptional cases, including IRF-2, HOXA7, and DMRT3. The results obtained using TGAS III had similar properties.
Gain and loss of activities during HSC progression
To analyze the change of TFBS activities between LT- and ST-HSCs, we tested 2 RC ensembles of a TFBS using a two-sample t-test under the null hypothesis that the mean values were equal. This analysis found that the null hypothesis was rejected for 71 TFBSs (Class A) and 58 TFBSs (Class B) (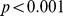 ) (Figure 3B). The multiple-testing correction reduced these numbers to 49 and 42 in Class A and Class B, respectively (
) (Figure 3B). The multiple-testing correction reduced these numbers to 49 and 42 in Class A and Class B, respectively (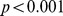 ) (Tables S8 and S9). Interestingly, although these TFBSs had different mean values, the effects of the activities were mostly unchanged; a positive (negative) activity in LT-HSC was still positive (negative) in ST-HSC, i.e., 75% (53/71) in Class A and 84% (49/58) in Class B. In most cases, the strengths of these activities increased markedly in ST-HSC, i.e., 85% (45/53) in Class A and 76% (37/49) in Class B. These results suggest that the maintenance of self-renewal and the differentiation competence in ST-HSCs require a vigorous transcriptional program.
) (Tables S8 and S9). Interestingly, although these TFBSs had different mean values, the effects of the activities were mostly unchanged; a positive (negative) activity in LT-HSC was still positive (negative) in ST-HSC, i.e., 75% (53/71) in Class A and 84% (49/58) in Class B. In most cases, the strengths of these activities increased markedly in ST-HSC, i.e., 85% (45/53) in Class A and 76% (37/49) in Class B. These results suggest that the maintenance of self-renewal and the differentiation competence in ST-HSCs require a vigorous transcriptional program.
As an intuitive insight into the gain and loss of activities during HSC progression, we found that downregulation of Class A in ST-HSC relative to LT-HSC was accompanied by a gain of negative RCs in ST-HSC (e.g., CKROX, GABP, C/EBPdelta, and myogenin/NF-1) and by a loss of positive RCs in LT-HSC (e.g., IRF-2, HEN1, POU6F1, and RBP-jkappa). Similarly, upregulation of Class B in ST-HSC relative to LT-HSC was followed by a gain of positive RCs in ST-HSC (e.g., SF1, Oct-4, GATA-6, and RORalpha) and by a loss of negative RCs in LT-HSC (e.g., PBX1, IPF1, MYB, KAISO, and Pax-4). However, many of the TFBSs in each class exhibited activity changes that differed greatly from our intuitive expectations, which suggests that the high level of complexity in the transcriptional circuit is related to context-dependent gene expression.
Functional importance of TFs coded by rare transcripts
Regulatory effects of TFs from gene classes that were expressed at low and undetectable levels
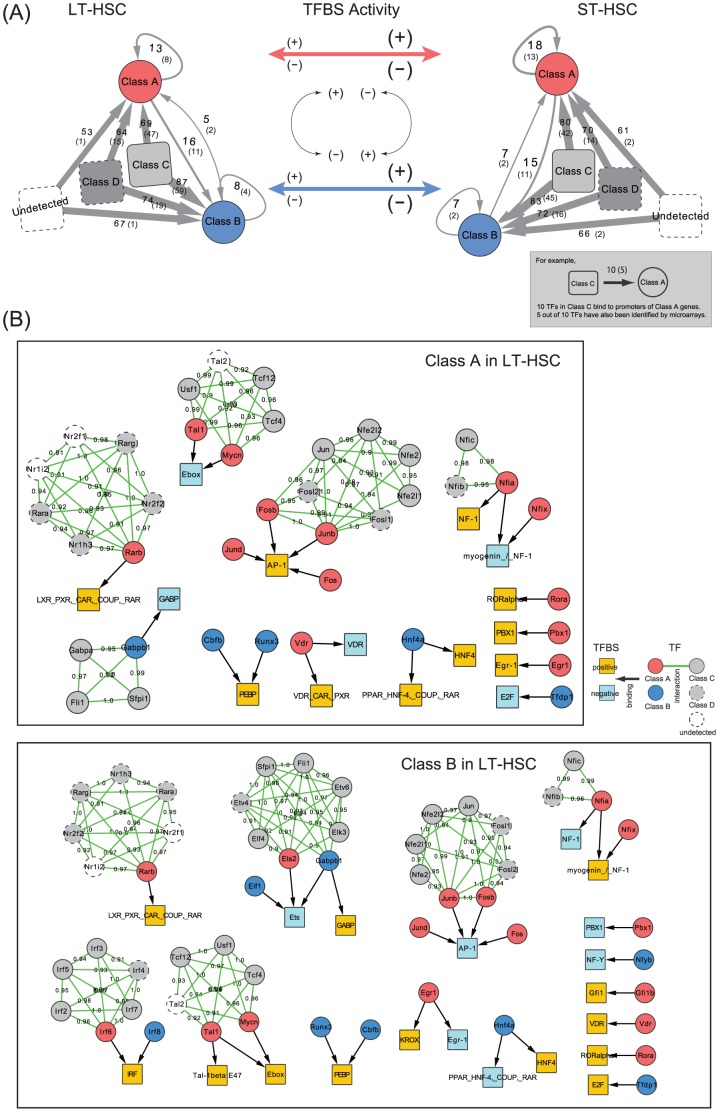
We constructed TF–gene networks on the basis of the links between the 142 TFBSs and their downstream target genes. The networks had vast numbers of edges: 40,896 edges among 204 TFs that targeted 114 TFBSs of Class A in LT-HSC; 45,882 edges among 237 TFs that targeted 114 TFBSs of Class A in ST-HSC; 97,946 edges among 253 TFs that targeted 134 TFBSs of Class B in LT-HSC; and 96,975 edges among 243 TFs that targeted 125 TFBSs of Class B in ST-HSC.
The majority of TFs involved in these networks belonged to Class D and transcripts that were not detected in our RNA-seq assay (Figure 4A). Only a small portion of these genes were detected by microarray analyses [8], [9], i.e., the numbers in parentheses in Figure 4A. Our qRT-PCR assay detected only 1 or 2 of these genes, suggesting that they originated from rare transcripts, i.e., TF-coding genes expressed at low or undetectable levels in HSCs. To assess the importance of these TFs, we modified TGAS V to remove the regulatory effects from the TFs; by setting 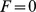 (Equation 8) for unexpressed TF-coding genes (TGAS V-1) and for TF-coding genes in Class D (TGAS V-2). As a result, Rs were lower than TGAS V when the model removed these effects (Table 2), which suggests their important contribution to the modeling. Indeed, many known factors [17], [46] were present in these categories.
(Equation 8) for unexpressed TF-coding genes (TGAS V-1) and for TF-coding genes in Class D (TGAS V-2). As a result, Rs were lower than TGAS V when the model removed these effects (Table 2), which suggests their important contribution to the modeling. Indeed, many known factors [17], [46] were present in these categories.
Figure 4. Inference of transcriptional regulatory networks.
(A) Systematic representation of TF–gene networks and the change of TFBS activities between LT-HSCs and ST-HSCs. Genes that produce TFs that putatively bind to important TFBSs (Figure 3A) existed in each class. Some of them were not detected in the RNA-seq assay, and were categorized as ''Undetected''. The numbers on the gray-colored arrows denote the number of TFs in the corresponding class that bind to Class A or B gene promoters, suggesting that the majority of TFs belonged to nondifferentially expressed gene classes. The numbers in parentheses indicate TFs that were detected in microarray-based studies, suggesting the extensive discovery of our assay. As shown in the middle panel, we inferred that the positive or negative activities of TFBSs are mostly unchanged between cells, but are inverted between Class A and Class B. (B) Subnetworks of (A) in LT-HSCs. The majority of TF-coding genes were not differentially expressed, whereas 24 TFs binding to 21 TFBSs were present among DEGs (Class A and Class B) and interacted strongly with nondifferentially expressed TFs (Figure S4 shows the subnetworks in ST-HSCs).
Competitive repopulation assay with activated Pparg
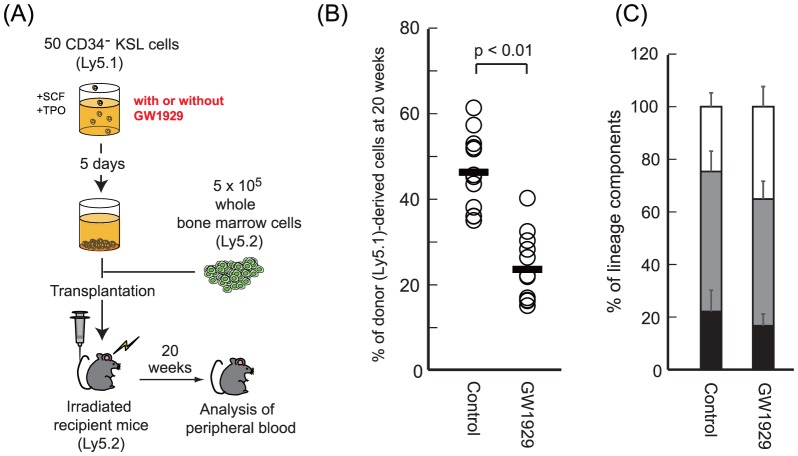
The suggestion that TF-coding genes expressed at low levels are important contributors to transcriptional regulation prompted us to investigate the function of Pparg, which remains controversial in HSC biology [47]. Pparg was categorized into Class D (0.3747 FPKM in LT-HSC and 0.2616 FPKM in ST-HSC), and its binding site PPARG had negative RCs in all 4 models (Figure 3A). To confirm this PPARG activity, we treated LT-HSCs with GW1929, a high agonist of Pparg [48], [49].
As shown in Figure 5A, we performed a transplantation assay using LT-HSCs that were cultured for 5 days with or without GW1929. GW1929-treated HSCs exhibited decreased chimerism at 20 weeks after the transplantation compared with the controls (Figure 5B). The contribution of T-cell, B-cell, and myeloid lineages to the total donor-derived cells was not highly different (Figure 5C). These results suggest the possibility that the excessive activity of PPARG influences negatively the long-term repopulating activity of HSCs, which supports the capacity of our approach to infer the activities of regulatory elements in HSCs.
Figure 5. Long-term competitive reconstitution assay.
(A) Scheme of the competitive repopulation assay using GW1929, a high agonist of Pparg. (B) Analysis of the proportion of donor-derived 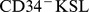 HSCs obtained from untreated (Control) and treated (GW1929) recipient mice at 20 weeks posttransplant. Each dot represents a single mouse. (C) Relative contributions of
HSCs obtained from untreated (Control) and treated (GW1929) recipient mice at 20 weeks posttransplant. Each dot represents a single mouse. (C) Relative contributions of 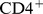 or
or 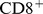 (T-cell lineage),
(T-cell lineage), 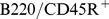 (B-cell lineage) and Mac-1+ or Gr-1+ (myeloid lineage) cells in donor-derived Ly-5.1+ cells of recipient mice at 20 weeks posttransplant. Black, T-cell lineage; gray, B-cell lineage; white, myeloid lineage. Data are presented as the mean
(B-cell lineage) and Mac-1+ or Gr-1+ (myeloid lineage) cells in donor-derived Ly-5.1+ cells of recipient mice at 20 weeks posttransplant. Black, T-cell lineage; gray, B-cell lineage; white, myeloid lineage. Data are presented as the mean  .
.
Identification of potential key regulators
Differentially expressed TFs and their target sites
The regulatory networks (Figure 4A) involved differentially expressed TFs, i.e., 18 TFs regulated Class A in LT-HSC (13 from Class A and 5 from Class B) and 24 TFs regulated Class B in LT-HSC (16 from Class A and 8 from Class B). These TFs targeted 21 TFBSs that are well-studied hematopoietic regulators, including the Fos/Jun complex [50], Ebox-binding bHLH TFs [51], the GABP complex [52], and retinoic acid receptors [53]. In particular, AP-1 and Egr-1 appeared in all of the models and were targeted by immediate early response genes that are important for apoptosis and differentiation [50] and that are downregulated in ST-HSCs [54]. Interestingly, our model showed that some of these TFs are highly modulated by other TFs that were not differentially expressed (Figures 4B and S4). This may explain the observation that the models with TGAS V-1 and TGAS V-2 reduced the predictive performance.
Putative function of the differentially expressed TFs
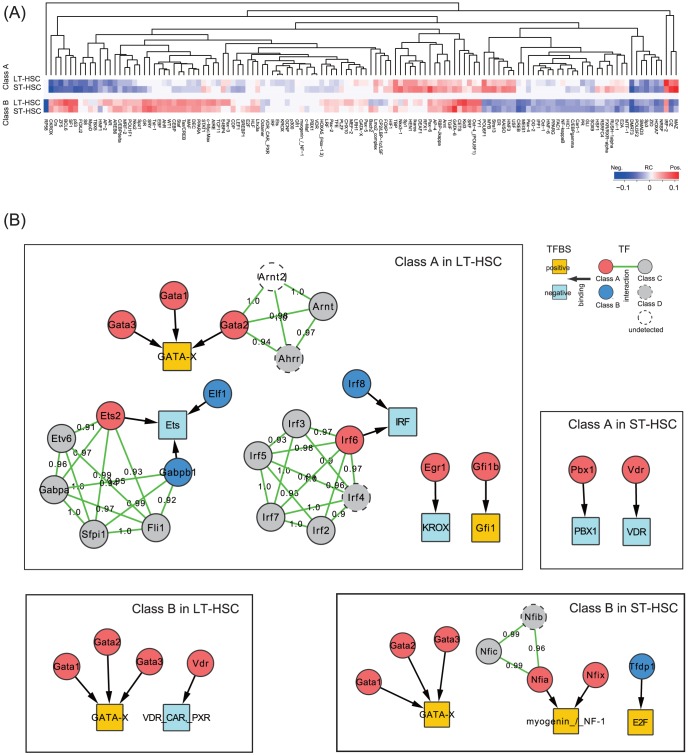
Many recent studies have reported that epigenetic effects are important factors in hematopoiesis [16], [18], [55]. What would happen if the 21 TFBSs targeted by differentially expressed TFs were turned off by DNA methylation, for example? This question was suggested by the recent finding that CpG-methylated regions colocalize with TFBSs in HSCs [56]. To answer this question, we removed each set of TFBSs that appeared in Figures 4B and S4, and performed regression modeling in this condition. The results showed slightly lower Rs (TGAS V-3 in Table 2), however, the overall propensity of the activities was not different from those shown in Figure 3A (Figure 6A).
Figure 6. Alternative regulators potentially important in the presence of dysfunctional TFBSs that are targeted by differentially expressed TFs.
(A) Heat map showing the regression coefficients (RCs) of 129 potentially important TFBSs (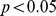 ) that were identified after the removal of the TFBSs in Figures 4B and S4. The overall propensity of TFBS activities were not different from those shown in Figure 3A. (B) This removal test identified subnetworks that involve alternative TFBSs targeted by differentially expressed TFs. These included GATA-X, Ets, and IRF, which are related to erythroid/megakaryocytic lineage commitment; 6 TFBSs were targeted by 11 TFs in LT-HSCs, and 5 TFBSs were targeted by 8 TFs in ST-HSCs.
) that were identified after the removal of the TFBSs in Figures 4B and S4. The overall propensity of TFBS activities were not different from those shown in Figure 3A. (B) This removal test identified subnetworks that involve alternative TFBSs targeted by differentially expressed TFs. These included GATA-X, Ets, and IRF, which are related to erythroid/megakaryocytic lineage commitment; 6 TFBSs were targeted by 11 TFs in LT-HSCs, and 5 TFBSs were targeted by 8 TFs in ST-HSCs.
Interestingly, specific TFBSs (e.g., GATA-X, Ets, and IRF) that were targeted by differentially expressed TFs were determined (Figure 6B). The most remarkable change was that GATA-X acquired positive activities in LT-HSCs. It is well known that GATA and AP-1 frequently co-occupy chromatin sites and that they play critical roles in cell fate decisions to commit to erythroid vs. myeloid lineages [57], [58]. More recent studies have shown that epigenetic marks control the interactions among Gata factors and other hematopoietic TFs [55], and that the DNA methylation patterns of the GATA and AP-1 motifs are mutually exclusive during early hematopoiesis [56].
Overall, our results suggest that the 24 TFs that target 21 TFBSs (Figure 4B) are key regulators of HSCs. The ST-HSCs used here exhibited lymphoid-priming features [8] with preferentially repressive potential megakaryocyte/erythroid genes (Table S7). Therefore, these regulators may be related to lymphoid-lineage development. Our model showed that dysfunctions in these regulators led to alternative regulators related to erythroid/megakaryocytic lineage development competence. This supports the recent remarkable finding of a novel lineage commitment pathway [4].
Discussion
HSC fate is controlled tightly by extrinsic and intrinsic factors [1], [2], [10]-[12], [36]. The identification and characterization of these factors may lead to more effective clinical therapies for acquired and congenital blood disorders. Owing to recent advances in experimental and computational techniques, many recent studies [3], [4], [25] have begun to move beyond the traditional beliefs regarding hematopoiesis. However, the determination of the upstream regulatory elements that are responsible for the development of the hematopoietic system remains far from adequate and requires the application of various approaches. In the present study, we established novel transcriptome profiles from mouse LT- and ST-HSCs using an RNA-seq assay and developed a computational method for exploring the potential modes of transcriptional regulation based on these profiles.
Our RNA-seq assay confirmed the transcriptionally active state of ST-HSCs [6], [7], [15] with markedly high numbers of DEGs. These DEGs included 77 cell-surface molecules and 57 TFs (Tables 1 and S2–S5), which indicates that specific extrinsic and intrinsic regulators respond actively during the transition between LT- and ST-HSCs. During this transition, we observed that many previously annotated lineage-specific genes [8] were up- and downregulated (Table S7). In particular, lymphoid potential genes that preferentially undergo upregulation in ST-HSCs and potential megakaryocyte/erythroid genes had opposite patterns, suggesting that lymphoid priming occurs during this early stage.
To investigate the regulatory activities of known factors, we conducted a preliminary study using our previous method [29] and ChIP-seq data for 10 major hematopoietic regulators [17]; however, we were unable to obtain any significant results (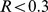 ). This failure prompted us to extend our approach in the following manner (Figure 2). To approximate TFBS activities, we employed cis- and trans-regulatory information from TRANSFAC [39]. Furthermore, to consider the combinatorial regulation of TFs, we incorporated the probabilities of the conditional TF–TF interactions inferred by LLM [31]. Thus, our approach systematically inferred the regulatory activities of TFBSs, and suggested potential synergistic TF modules. Consequently, we found that motif similarity, the positional distribution of motifs, and expression changes in TFs were the most informative features for the promoter modeling of DEGs. Using LLM, we quantified the TFBS activities on the basis of the fine-tuned explanations of DEGs (TGAS V in Table 2).
). This failure prompted us to extend our approach in the following manner (Figure 2). To approximate TFBS activities, we employed cis- and trans-regulatory information from TRANSFAC [39]. Furthermore, to consider the combinatorial regulation of TFs, we incorporated the probabilities of the conditional TF–TF interactions inferred by LLM [31]. Thus, our approach systematically inferred the regulatory activities of TFBSs, and suggested potential synergistic TF modules. Consequently, we found that motif similarity, the positional distribution of motifs, and expression changes in TFs were the most informative features for the promoter modeling of DEGs. Using LLM, we quantified the TFBS activities on the basis of the fine-tuned explanations of DEGs (TGAS V in Table 2).
Many hematopoietic TFs [6], [17] were included among the transcriptional steady-state gene set (Class C), the low-level expression gene set (Class D), or the genes expressed at undetectable levels. Throughout this study, we found that the regulatory effects of these TFs and their target sites are essential to explain the regulation of DEGs. This may explain, in part, the observation that our preliminary model using 10 major hematopoietic TFs was not well fitted. We further supported this finding by performing a transplantation assay of LT-HSCs cultured with activated Pparg (Figure 5). Furthermore, we found that these TFs modulated differentially expressed TFs that are likely to be important during commitment to specific lineages (Figures 4B and 6B). However, LLM inferred low probabilities for interactions between known co-operative TF pairs (Tables S12 and S13), e.g., Gata2 and Erg (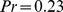 in Classes A and B) and Gata2 and Tal1 (
in Classes A and B) and Gata2 and Tal1 (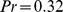 in Class A,
in Class A, 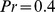 in Class B), which suggests that their co-operation regulates specific gene sets.
in Class B), which suggests that their co-operation regulates specific gene sets.
We identified 142 TFBSs that contributed significantly to the regression models (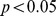 ). Among these, 71 TFBSs (Class A) and 58 TFBSs (Class B) exhibited a considerable gain or loss of their activities during cell differentiation (
). Among these, 71 TFBSs (Class A) and 58 TFBSs (Class B) exhibited a considerable gain or loss of their activities during cell differentiation (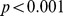 ). As illustrated in Figure 4A, the effects of TFBS activities represented by plus or minus signs of RCs were mostly unchanged between cells but were inverted between DEGs. The strengths of TFBS activities increased markedly in ST-HSCs compared with LT-HSCs. We applied our method to 2 public RNA-seq datasets that represented sequential cell development (MII oocytes and two-cell embryos) and lineage commitment (megakaryocyte/erythroid precursors and megakaryocytes) (Figure S5). This analysis showed that the results of cell-lineage commitment agreed with the propensity of the regulatory activities detected in HSCs, rather than with that of sequential cell development. Therefore, regulators that play similar or different roles in accordance with cellular contexts might be general features that underlie cell fate decisions.
). As illustrated in Figure 4A, the effects of TFBS activities represented by plus or minus signs of RCs were mostly unchanged between cells but were inverted between DEGs. The strengths of TFBS activities increased markedly in ST-HSCs compared with LT-HSCs. We applied our method to 2 public RNA-seq datasets that represented sequential cell development (MII oocytes and two-cell embryos) and lineage commitment (megakaryocyte/erythroid precursors and megakaryocytes) (Figure S5). This analysis showed that the results of cell-lineage commitment agreed with the propensity of the regulatory activities detected in HSCs, rather than with that of sequential cell development. Therefore, regulators that play similar or different roles in accordance with cellular contexts might be general features that underlie cell fate decisions.
Overall, our results suggest that HSCs exhibit flexible and rapid responses to local needs by controlling TFs that are expressed at steady-state or low levels via a highly complex regulatory network. Further studies should consider the implications of these regulatory modes based on instructive and/or stochastic models of stem cell fate decisions. In the present study, we demonstrated that specific lineage-affiliated TFs formed a resultant set of transcriptional regulation, i.e., 24 differentially expressed TFs that contributed significantly to the model were modulated by other TFs that were not differentially expressed. These TFs include immediate early genes (e.g., Fos, Jun, and Egr1) that induce an early genomic response related to HSC biology [50], [54]. If they become dysfunctional, LT-HSCs may be primed to an erythroid/megakaryocytic lineage via pathways that are controlled by other TFs (e.g., Gata factors, ETS family, and IRF family).
In summary, we obtained novel transcriptome data and developed a computational method for promoter modeling. Our method can be applied easily to other biological systems. Using these approaches, we identified transcriptional regulation modes that provide insights into how HSCs determine their phenotype. Future works that overcome the limitations of the present study, such as the inclusion of enhancer activities that appear to be important in hematopoiesis [17], [42] and the analysis of the influence of transcriptional heterogeneity at the single-cell level [4], [10], [34], which can be assayed using promising techniques [59]–[61], would refine our findings and advance our understanding of the kinetic and regulatory aspects of stem cell biology.
Materials and Methods
Animals
All experimental protocols were reviewed and approved by the Institutional Animal Care and Use Committee of Tokyo Women's Medical University (approval ID: 13-99-2-B). Mice were purchased from Sankyo Labo Service.
Cell collection
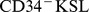 (c-kit+Sca1+Lin−) LT-HSCs or
(c-kit+Sca1+Lin−) LT-HSCs or 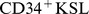 ST-HSCs were sorted, as described previously [36]. In brief, we isolated bone marrow cells from 8- to 10-week-old C57BL/6 mice and stained them with antibodies for CD34 (RAM34, eBiosciences, San Diego, CA), Sca-1 (E13-161.7, BD Biosciences Pharmingen, San Jose, CA), c-kit (2B8, BD Biosciences Pharmingen), and a lineage marker (Lineage Detection Kit, Miltenyi Biotec Inc., Bergisch Gladbach, Germany). Subsequently, we analyzed the stained cells using a MoFlo XDP cell sorter system (Beckman Coulter, Fullerton, CA).
ST-HSCs were sorted, as described previously [36]. In brief, we isolated bone marrow cells from 8- to 10-week-old C57BL/6 mice and stained them with antibodies for CD34 (RAM34, eBiosciences, San Diego, CA), Sca-1 (E13-161.7, BD Biosciences Pharmingen, San Jose, CA), c-kit (2B8, BD Biosciences Pharmingen), and a lineage marker (Lineage Detection Kit, Miltenyi Biotec Inc., Bergisch Gladbach, Germany). Subsequently, we analyzed the stained cells using a MoFlo XDP cell sorter system (Beckman Coulter, Fullerton, CA).
RNA sequencing and real-time PCR
After obtaining total RNA extracts from 5000 LT- or ST-HSCs using Isogen (Nippon Gene, Tokyo, Japan) in triplicate, we synthesized cDNA using a SMARTer Pico cDNA amplification kit (Clonetech, Mountain View, CA) and amplified them with 20 cycles of PCR. Using the standard protocols for the SOLiD system, we sequenced the amplified cDNA using a SOLiD sequencer (Life Technologies, Carlsbad, CA), as described previously [36]. In the RT-PCR assay, total RNA was obtained from the sorted cells and cDNA was synthesized as described above. We performed RT-PCR using a TaqMan Gene Expression Assay (Life Technologies) for the genes indicated with the BioMark HD system (Fludigm, South San Francisco, CA).
Read mapping and quantification
We used the TopHat (v1.4.1)/Cufflinks (v.2.0.2) pipeline [33] with the sequenced reads (quality score, 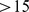 ). The pipeline was coupled to Bowtie (v.0.12.7) [62]. We employed the recursive read mapping method, as described previously [32]. In brief, we applied TopHat by truncating the
). The pipeline was coupled to Bowtie (v.0.12.7) [62]. We employed the recursive read mapping method, as described previously [32]. In brief, we applied TopHat by truncating the 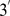 ends of unmapped reads and by realigning the reads using more stringent parameters. We set the parameters empirically, which were used sequentially, as the read length, ''-initial-read-mismatches'', ''-segment-mismatches'', and ''-segment-length'': (50, 3, 2, 25), (46, 3, 2, 23), (42, 3, 2, 21), (38, 2, 0, 19), and (34, 2, 0, 17).
ends of unmapped reads and by realigning the reads using more stringent parameters. We set the parameters empirically, which were used sequentially, as the read length, ''-initial-read-mismatches'', ''-segment-mismatches'', and ''-segment-length'': (50, 3, 2, 25), (46, 3, 2, 23), (42, 3, 2, 21), (38, 2, 0, 19), and (34, 2, 0, 17).
The pipeline, which quantifies RNA abundance as fragments per kilobase of exon per million mapped reads (FPKM), mapped sequenced reads to the mouse genome (mm9), and then assembled transcripts with uniquely mapped reads (uni-reads) for each replicate. We used Cuffcompare to merge all the transcript assemblies; 14,728 and 14,128 RefSeq-annotated genes in LT- and ST-HSCs, respectively. Using the merged transcript assembly, we performed Cuffdiff, which calculates FPKMs across all replicates and detects DEGs via two-group t-tests coupled to a Benjamini–Hochberg false discovery rate (FDR) procedure. We further used transcripts that satisfied the following conditions: successful deconvolution, FDR of 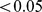 , complete match of intron chain, and FPKM of
, complete match of intron chain, and FPKM of 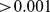 . The mouse genome and RefSeq annotation were downloaded from http://genome.ucsc.edu/.
. The mouse genome and RefSeq annotation were downloaded from http://genome.ucsc.edu/.
Long-term competitive reconstitution assay
We cultured 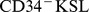 HSCs derived from C57BL/6-Ly5.1 congenic mice for 5 days with or without
HSCs derived from C57BL/6-Ly5.1 congenic mice for 5 days with or without 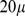 M GW1929 (Sigma-Aldrich, St. Louis, MO) in S-Clone SF-03 medium (Sanko-Junyaku Co., Tokyo, Japan) supplemented with 0.5% bovine serum albumin (Sigma, St. Louis, MO) and 50 ng/ml mouse stem cell factor and 50 ng/ml mouse TPO (all from R&D systems, Minneapolis, MN). Next, we performed a long-term competitive reconstitution assay by transplanting cultured cells with
M GW1929 (Sigma-Aldrich, St. Louis, MO) in S-Clone SF-03 medium (Sanko-Junyaku Co., Tokyo, Japan) supplemented with 0.5% bovine serum albumin (Sigma, St. Louis, MO) and 50 ng/ml mouse stem cell factor and 50 ng/ml mouse TPO (all from R&D systems, Minneapolis, MN). Next, we performed a long-term competitive reconstitution assay by transplanting cultured cells with 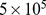 whole bone marrow competitor cells derived from C57BL/6-Ly5.2 Wt mice into lethally irradiated (9.5 Gy) C57BL/6-Ly5.2 Wt mice.
whole bone marrow competitor cells derived from C57BL/6-Ly5.2 Wt mice into lethally irradiated (9.5 Gy) C57BL/6-Ly5.2 Wt mice.
Log-linear model (LLM)
Suppose that we consider binary-stated (absence or presence) TFs {A, B, C}. The observed counts fall into 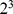 -dimensional contingency table by cross-classifying the TF states. The full model (FM), which contains all the possible interactions, gives the logarithms of probabilities as follows:
-dimensional contingency table by cross-classifying the TF states. The full model (FM), which contains all the possible interactions, gives the logarithms of probabilities as follows:
| (1) |
where i, j and k are the state indices of {A, B, C}, 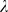 s are unknown parameters,
s are unknown parameters, 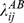 ,
, 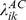 and
and 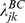 represent the interaction effects among the indexed variables. If an instance of A is independent of B, FM can be reduced to a reduced model (RM) with respect to the hierarchy [31], which is given as follows:
represent the interaction effects among the indexed variables. If an instance of A is independent of B, FM can be reduced to a reduced model (RM) with respect to the hierarchy [31], which is given as follows:
| (2) |
This model can be reformulated as
| (3) |
where ''+'' denotes the summation over the corresponding index. This formula is equivalent to 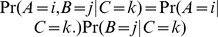 , which means that A and B are independent in the conditional distribution given C (
, which means that A and B are independent in the conditional distribution given C (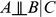 ).
).
To find the most parsimonious RM, we remove an interaction term from the current model and measure two p-values for the asymptotic 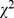 test of a likelihood ratio
test of a likelihood ratio 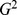 statistic [31]. The p-values comprise p_FM, which is the difference between FM and RM, and p_RM, which is the difference between the current model and RM. We accept a removal if it yields the largest p_RM (
statistic [31]. The p-values comprise p_FM, which is the difference between FM and RM, and p_RM, which is the difference between the current model and RM. We accept a removal if it yields the largest p_RM (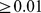 ), and we terminate if any removal test yields
), and we terminate if any removal test yields 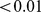 for either p_RM or p_FM.
for either p_RM or p_FM.
Iterative random sampling for LLM
A large number of TFs can easily yield a vast dimensional contingency table. To find a near optimal parsimonious model even in such higher-dimensional space, we designed an iterative sampling scheme that allowed us to calculate interaction probability Pr as follows.
Let 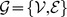 is an undirected graph, where
is an undirected graph, where 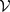 is a finite set of vertices (TFs) and
is a finite set of vertices (TFs) and 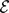 is a set of edges, which represent the interactions between vertex pairs. The scheme is as follows.
is a set of edges, which represent the interactions between vertex pairs. The scheme is as follows.
1.
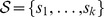 , a nonredundant combination of TFs, is selected randomly from all TFs (
, a nonredundant combination of TFs, is selected randomly from all TFs (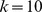 in the present study).
in the present study).For all possible vertex pairs
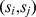 , the trial number
, the trial number 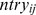 of an edge between
of an edge between 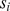 and
and 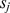 is counted (i.e., FM of k variables).
is counted (i.e., FM of k variables).LLM infers the best model
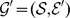 , where
, where 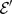 is a set of edges that represents TF–TF interactions.
is a set of edges that represents TF–TF interactions.For all possible vertex pairs
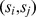 , if an edge in
, if an edge in 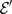 links a pair
links a pair 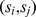 , the observed edge frequency
, the observed edge frequency 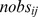 for this pair is counted.
for this pair is counted.For all possible vertex pairs
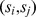 , the interaction probability Pr for a pair
, the interaction probability Pr for a pair 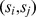 is updated using
is updated using 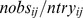 .
.If
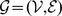 , where
, where 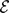 is a set of edges (
is a set of edges (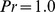 ), is not changed with a large number of samplings (
), is not changed with a large number of samplings (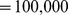 ); therefore, this procedure is terminated. Otherwise, steps 1–5 are repeated.
); therefore, this procedure is terminated. Otherwise, steps 1–5 are repeated.
Linear regression model
We used a multivariate regression model
| (4) |
| (5) |
where 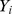 is the expression of gene i,
is the expression of gene i, 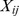 is TGAS of the jth TFBS in the promoter region of gene i,
is TGAS of the jth TFBS in the promoter region of gene i, 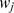 is RC of the jth TFBS, and
is RC of the jth TFBS, and 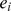 is the error term. TGAS is the sum of scores
is the error term. TGAS is the sum of scores 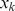 , where k represents the position of the jth TFBS in promoter i. We tested the following forms of
, where k represents the position of the jth TFBS in promoter i. We tested the following forms of 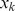 .
.
I: matrix similarity s of TFBS j scored using MATCH [43] (
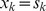 ).
).- II: TGAS I modified by a location-dependent weight L,
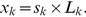
(6) - III: TGAS II weighted by the expression fold change (F) of TFs,
where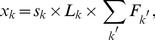
(7) 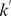 is the index of TFs binding to TFBS j. If FPKM for TF is
is the index of TFs binding to TFBS j. If FPKM for TF is 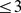 , we use
, we use 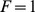 .
. IV: the same as TGAS III, but we removed TFBSs where none of the TFs had FPKM of
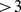 .
.- V: TGAS III weighted using both Fs of interactive TFs and the interaction probability Pr estimated by LLM,
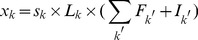
(8) 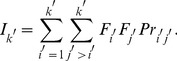
(9)
We used a published method to calculate L
[40]. First, we calculated the distribution of TFBS j in bins ( = 500 bp) of promoter regions and created a histogram  . Next, we randomized the positions of TFBS j and created a histogram
. Next, we randomized the positions of TFBS j and created a histogram 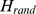 . L for the kth TFBS j is given by the following:
. L for the kth TFBS j is given by the following:
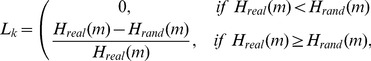 |
(10) |
where m represents the index of bin that corresponds to the position of the kth TFBS j. This location-dependent weight takes a value between 0 and 1, where a higher weight implies nonrandom occurrence.
Stepwise selection of the regression model
We built a regression model with the explanatory variable X and then reduced the model using AIC. Let the reduced model be  with
with  .
. 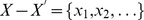 is the variables removed on the basis of AIC. V is the set of all pairwise terms of
is the variables removed on the basis of AIC. V is the set of all pairwise terms of 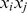 (
(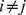 ). We searched any elements of V that improve Pearson's correlation coefficient
). We searched any elements of V that improve Pearson's correlation coefficient  of 5-fold CV on testing datasets.
of 5-fold CV on testing datasets.
Randomly select
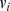 (
(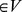 ) and add it to
) and add it to 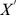 , which yields
, which yields 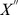 .
.Perform 5-fold CV with
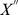 and calculate the averaged r on testing datasets.
and calculate the averaged r on testing datasets.If the r has been improved, update
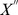 to
to 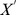 .
.Repeat step 1–3 until all
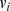 have been tested.
have been tested.Calculate Pearson's correlation coefficient R between observed and predicted FPKMs of all genes by using the final model.
We run this procedure 100 times using different random seeds. The final R is referred to as a model quality in this study.
Bioinformatics analysis
We obtained array-based gene expression profiles [8], [9] from BloodExpress [63], RNA-seq data for megakaryocyte/erythroid precursors and megakaryocytes from http://genome.ucsc.edu/encode/, and RNA-seq data for MII oocytes and two-cell embryos from DDBJ DRA001066. The public RNA-seq datasets were analyzed using the pipeline mentioned above. To search putative TFBSs and TFs in TRANSFAC professional (released in January 2013) [39], we prepared 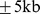 DNA sequences from transcription start sites (TSSs) annotated in RefSeq (http://www.ncbi.nlm.nih.gov/refseq/), and applied the MATCH tool in the minimize false-positive mode [43].
DNA sequences from transcription start sites (TSSs) annotated in RefSeq (http://www.ncbi.nlm.nih.gov/refseq/), and applied the MATCH tool in the minimize false-positive mode [43].
To analyze the enriched GO terms, we used the DAVID Bioinformatics Resources [35]. Significant terms detected by DAVID (EASE score, a modified Fisher's exact p-value, 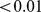 ) were grouped into representative ancestor terms in the dataset GO Slim2 using CateGOrizer [64]. We used the R programming language (http://www.r-project.org/) for regression modeling and to perform statistical tests. Although all p-values were adjusted by Bonferroni correction (Tables S6 and S8–S11), we used uncorrected p-values throughout this study to avoid too conservative interpretation that would reduce biologically meaningful findings.
) were grouped into representative ancestor terms in the dataset GO Slim2 using CateGOrizer [64]. We used the R programming language (http://www.r-project.org/) for regression modeling and to perform statistical tests. Although all p-values were adjusted by Bonferroni correction (Tables S6 and S8–S11), we used uncorrected p-values throughout this study to avoid too conservative interpretation that would reduce biologically meaningful findings.
Data access
The RNA-seq data generated in this study have been deposited in the DDBJ (DNA Data Bank of Japan) Sequence Read Archive (DRA) under accession number DRA001213. The online version of LLM is available at http://dbtmee.hgc.jp/tools/.
Supporting Information
Correlation analysis of gene expression levels measured using RNA-seq assays. (A) Reproducibility based on triplicate analyses of LT- and ST-HSCs. (B) Comparison of the gene expression correlations in the present study to those reported by Karlsson et al. [15], who purified HSCs using CD48−, CD150+, CD34−, CD9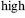 KSL for LT-HSCs and CD48−, CD150+, CD9
KSL for LT-HSCs and CD48−, CD150+, CD9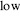 KSL for ST-HSCs.
KSL for ST-HSCs.
(EPS)
Contribution of higher-order TF interaction scores estimated by LLM. (A) Statistical differences of 2 regression coefficient (RC) ensembles of a TFBS found commonly by TGAS III and V (two-sample t-test). (B) Distribution of the TF interaction score 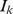 in Equation 9.
in Equation 9.
(EPS)
Box plots of RCs estimated by 100 iterations of regression modeling with TGAS V. Pos and Neg represent the positive (red) and negative (blue) mean values of RCs (red line), respectively.
(EPS)
Subnetworks involved in ST-HSC regulation. Although the majority of TF-coding genes found in ST-HSCs (Figure 4A) were not differentially expressed, 26 differentially expressed TFs that putatively bind to 21 TFBSs were present among DEGs (Class A and Class B).
(EPS)
Propensity of the TFBS activities inferred from public RNA-seq datasets. We applied our method to public RNA-seq datasets related to sequential cell development (A) and lineage commitment (C). Our procedure evaluates the averaged R of 5-fold CV on testing datasets (blue line). If a model improved R in testing, the model was accepted and its R value between the observed and predicted gene expression of all genes was measured (red line). (B) Of 147 TFBSs (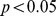 ), 67 TFBSs (Class A; upregulated in Oo) and 80 TFBSs (Class B; upregulated in 2C) exhibited significant gains and losses of activity (
), 67 TFBSs (Class A; upregulated in Oo) and 80 TFBSs (Class B; upregulated in 2C) exhibited significant gains and losses of activity (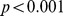 ). In addition, 73% (49/67) of Class A and 52.5% (42/80) of Class B genes exhibited no changes in the effects of their TFBS activities between cells, i.e., positive (negative) in Oo was still positive (negative) in 2C. We found that 16% (8/49) of Class A and 83% (35/42) of Class B genes had increased activities in 2C compared with Oo. (D) Among 150 TFBSs (
). In addition, 73% (49/67) of Class A and 52.5% (42/80) of Class B genes exhibited no changes in the effects of their TFBS activities between cells, i.e., positive (negative) in Oo was still positive (negative) in 2C. We found that 16% (8/49) of Class A and 83% (35/42) of Class B genes had increased activities in 2C compared with Oo. (D) Among 150 TFBSs (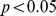 ), 98 TFBSs (Class A, upregulated in MEP) and 114 TFBSs (Class B, upregulated in Mk) exhibited significant gains and losses of activity (
), 98 TFBSs (Class A, upregulated in MEP) and 114 TFBSs (Class B, upregulated in Mk) exhibited significant gains and losses of activity (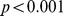 ). We also found that 83% (81/98) of Class A and 76% (87/114) of Class B genes exhibited no changes in the effects of their TFBS activities. All of the TFBSs in both classes exhibited increases in the strengths of their activities in Mk compared with MEP. R, Pearson's correlation coefficient; Oo, MII oocytes; 2C, 2-cell embryo; MEP, megakaryocyte/erythroid precursor; Mk, megakaryocyte.
). We also found that 83% (81/98) of Class A and 76% (87/114) of Class B genes exhibited no changes in the effects of their TFBS activities. All of the TFBSs in both classes exhibited increases in the strengths of their activities in Mk compared with MEP. R, Pearson's correlation coefficient; Oo, MII oocytes; 2C, 2-cell embryo; MEP, megakaryocyte/erythroid precursor; Mk, megakaryocyte.
(EPS)
RNA-seq mapping statistics.
(XLSX)
Differentially expressed cell-surface molecules.
(XLSX)
Differentially expressed transcription factors.
(XLSX)
Transcription factors categorized into Class C.
(XLSX)
Low expressed transcription factors (Class D).
(XLSX)
Average regression coefficient of 142 TFBSs.
(XLSX)
Classification of MkE, GM, and Lymphoid-associated genes.
(XLSX)
TFBSs significantly different in the regression coefficient between LT- and ST-HSCs (Class A).
(XLSX)
TFBSs significantly different in the regression coefficient between LT- and ST-HSCs (Class B).
(XLSX)
Enriched GO terms in Class A.
(XLSX)
Enriched GO terms in Class B.
(XLSX)
Result of log-linear model in Class A.
(XLSX)
Result of log-linear model in Class B.
(XLSX)
Acknowledgments
We thank Drs S. Mitani and T. Furukawa for their great help with RNA sequencing. Computational resources were provided by the supercomputer system at Human Genome Center, the Institute of Medical Science, the University of Tokyo.
Funding Statement
This work was supported by Research on Applying Health Technology, Health and Labour Sciences by the Ministry of Health, Labour and Welfare, Japan. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Hoang T (2004) The origin of hematopoietic cell type diversity. Oncogene 23: 7188–98. [DOI] [PubMed] [Google Scholar]
- 2. Forsberg EC, Bhattacharya D, Weissman IL (2006) Hematopoietic stem cells: expression profiling and beyond. Stem Cell Rev 2: 23–30. [DOI] [PubMed] [Google Scholar]
- 3. Sanjuan-Pla A, Macaulay IC, Jensen CT, Woll PS, Luis TC, et al. (2013) Platelet-biased stem cells reside at the apex of the haematopoietic stem-cell hierarchy. Nature 502: 232–6. [DOI] [PubMed] [Google Scholar]
- 4. Yamamoto R, Morita Y, Ooehara J, Hamanaka S, Onodera M, et al. (2013) Clonal analysis unveils self-renewing lineage-restricted progenitors generated directly from hematopoietic stem cells. Cell 154: 1112–26. [DOI] [PubMed] [Google Scholar]
- 5. Passegue E, Wagers AJ, Giuriato S, Anderson WC, Weissman IL (2005) Global analysis of proliferation and cell cycle gene expression in the regulation of hematopoietic stem and progenitor cell fates. J Exp Med 202: 1599–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Forsberg EC, Prohaska SS, Katzman S, Heffner GC, Stuart JM, et al. (2005) Differential expression of novel potential regulators in hematopoietic stem cells. PLoS Genet 1: e28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Zhong JF, Zhao Y, Sutton S, Su A, Zhan Y, et al. (2005) Gene expression profile of murine longterm reconstituting vs. short-term reconstituting hematopoietic stem cells. Proc Natl Acad Sci U S A 102: 2448–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Mansson R, Hultquist A, Luc S, Yang L, Anderson K, et al. (2007) Molecular evidence for hierarchical transcriptional lineage priming in fetal and adult stem cells and multipotent progenitors. Immunity 26: 407–19. [DOI] [PubMed] [Google Scholar]
- 9. Ficara F, Murphy MJ, Lin M, Cleary ML (2008) Pbx1 regulates self-renewal of long-term hematopoietic stem cells by maintaining their quiescence. Cell Stem Cell 2: 484–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kent DG, Copley MR, Benz C, Wohrer S, Dykstra BJ, et al. (2009) Prospective isolation and molecular characterization of hematopoietic stem cells with durable self-renewal potential. Blood 113: 6342–50. [DOI] [PubMed] [Google Scholar]
- 11. Chotinantakul K, Leeanansaksiri W (2012) Hematopoietic stem cell development, niches, and signaling pathways. Bone Marrow Res 2012: 270425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kunisaki Y, Bruns I, Scheiermann C, Ahmed J, Pinho S, et al. (2013) Arteriolar niches maintain haematopoietic stem cell quiescence. Nature 502: 637–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Liu P, Barb J, Woodhouse K, Taylor JG, Munson PJ, et al. (2011) Transcriptome profiling and sequencing of differentiated human hematopoietic stem cells reveal lineage-specific expression and alternative splicing of genes. Physiol Genomics 43: 1117–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lu R, Neff NF, Quake SR, Weissman IL (2011) Tracking single hematopoietic stem cells in vivo using high-throughput sequencing in conjunction with viral genetic barcoding. Nat Biotechnol 29: 928–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Karlsson G, Rorby E, Pina C, Soneji S, Reckzeh K, et al. (2013) The tetraspanin cd9 affords high-purity capture of all murine hematopoietic stem cells. Cell Rep 4: 642–8. [DOI] [PubMed] [Google Scholar]
- 16. Weishaupt H, Sigvardsson M, Attema JL (2010) Epigenetic chromatin states uniquely define the developmental plasticity of murine hematopoietic stem cells. Blood 115: 247–56. [DOI] [PubMed] [Google Scholar]
- 17. Wilson NK, Foster SD, Wang X, Knezevic K, Schutte J, et al. (2010) Combinatorial transcriptional control in blood stem/progenitor cells: genome-wide analysis of ten major transcriptional regulators. Cell Stem Cell 7: 532–44. [DOI] [PubMed] [Google Scholar]
- 18. Bissels U, Bosio A, Wagner W (2012) Micrornas are shaping the hematopoietic landscape. Haematologica 97: 160–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Whichard ZL, Sarkar CA, Kimmel M, Corey SJ (2010) Hematopoiesis and its disorders: a systems biology approach. Blood 115: 2339–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bonzanni N, Garg A, Feenstra KA, Schutte J, Kinston S, et al. (2013) Hard-wired heterogeneity in blood stem cells revealed using a dynamic regulatory network model. Bioinformatics 29: i80–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Hannah R, Joshi A, Wilson NK, Kinston S, Gottgens B (2011) A compendium of genome-wide hematopoietic transcription factor maps supports the identification of gene regulatory control mechanisms. Exp Hematol 39: 531–41. [DOI] [PubMed] [Google Scholar]
- 22. Novershtern N, Subramanian A, Lawton LN, Mak RH, Haining WN, et al. (2011) Densely interconnected transcriptional circuits control cell states in human hematopoiesis. Cell 144: 296–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Will B, Vogler TO, Bartholdy B, Garrett-Bakelman F, Mayer J, et al. (2013) Satb1 regulates the self-renewal of hematopoietic stem cells by promoting quiescence and repressing differentiation commitment. Nat Immunol 14: 437–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Mirshekar-Syahkal B, Haak E, Kimber GM, van Leusden K, Harvey K, et al. (2013) Dlk1 is a negative regulator of emerging hematopoietic stem and progenitor cells. Haematologica 98: 163–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Gazit R, Garrison B, Rao T, Shay T, Costello J, et al. (2013) Transcriptome analysis identifies regulators of hematopoietic stem and progenitor cells. Stem Cell Reports 1: 266–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Osawa M, Hanada K, Hamada H, Nakauchi H (1996) Long-term lymphohematopoietic reconstitution by a single cd34-low/negative hematopoietic stem cell. Science 273: 242–5. [DOI] [PubMed] [Google Scholar]
- 27. Ema H, Morita Y, Yamazaki S, Matsubara A, Seita J, et al. (2006) Adult mouse hematopoietic stem cells: purification and single-cell assays. Nat Protoc 1: 2979–87. [DOI] [PubMed] [Google Scholar]
- 28. Bussemaker HJ, Foat BC, Ward LD (2007) Predictive modeling of genome-wide mrna expression: from modules to molecules. Annu Rev Biophys Biomol Struct 36: 329–47. [DOI] [PubMed] [Google Scholar]
- 29. Park SJ, Nakai K (2011) A regression analysis of gene expression in es cells reveals two gene classes that are significantly different in epigenetic patterns. BMC Bioinformatics 12 Suppl 1S50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Irie T, Park SJ, Yamashita R, Seki M, Yada T, et al. (2011) Predicting promoter activities of primary human dna sequences. Nucleic Acids Res 39: e75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lauritzen S (1996) Graphical Models. New York: Oxford University Press.
- 32. Park SJ, Komata M, Inoue F, Yamada K, Nakai K, et al. (2013) Inferring the choreography of parental genomes during fertilization from ultralarge-scale whole-transcriptome analysis. Genes Dev 27: 2736–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Trapnell C, Roberts A, Goff L, Pertea G, Kim D, et al. (2012) Differential gene and transcript expression analysis of rna-seq experiments with tophat and cufflinks. Nat Protoc 7: 562–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Benz C, Copley MR, Kent DG, Wohrer S, Cortes A, et al. (2012) Hematopoietic stem cell subtypes expand differentially during development and display distinct lymphopoietic programs. Cell Stem Cell 10: 273–83. [DOI] [PubMed] [Google Scholar]
- 35. Huang DW, Sherman BT, Lempicki RA (2009) Systematic and integrative analysis of large gene lists using david bioinformatics resources. Nat Protoc 4: 44–57. [DOI] [PubMed] [Google Scholar]
- 36. Umemoto T, Yamato M, Ishihara J, Shiratsuchi Y, Utsumi M, et al. (2012) Integrin-alphavbeta3 regulates thrombopoietin-mediated maintenance of hematopoietic stem cells. Blood 119: 83–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Domen J, Cheshier SH, Weissman IL (2000) The role of apoptosis in the regulation of hematopoietic stem cells: Overexpression of bcl-2 increases both their number and repopulation potential. J Exp Med 191: 253–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Peng C, Chen Y, Shan Y, Zhang H, Guo Z, et al. (2012) Lsk derived lsk- cells have a high apoptotic rate related to survival regulation of hematopoietic and leukemic stem cells. PLoS One 7: e38614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Wingender E, Chen X, Hehl R, Karas H, Liebich I, et al. (2000) Transfac: an integrated system for gene expression regulation. Nucleic Acids Res 28: 316–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Chen X, Xu H, Yuan P, Fang F, Huss M, et al. (2008) Integration of external signaling pathways with the core transcriptional network in embryonic stem cells. Cell 133: 1106–17. [DOI] [PubMed] [Google Scholar]
- 41. Meissner A, Mikkelsen TS, Gu H, Wernig M, Hanna J, et al. (2008) Genome-scale dna methylation maps of pluripotent and differentiated cells. Nature 454: 766–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Moignard V, Macaulay IC, Swiers G, Buettner F, Schutte J, et al. (2013) Characterization of transcriptional networks in blood stem and progenitor cells using high-throughput single-cell gene expression analysis. Nat Cell Biol 15: 363–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Kel AE, Gossling E, Reuter I, Cheremushkin E, Kel-Margoulis OV, et al. (2003) Match: A tool for searching transcription factor binding sites in dna sequences. Nucleic Acids Res 31: 3576–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Boyle P, Despres C (2010) Dual-function transcription factors and their entourage: unique and unifying themes governing two pathogenesis-related genes. Plant Signal Behav 5: 629–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Whitfield TW, Wang J, Collins PJ, Partridge EC, Aldred SF, et al. (2012) Functional analysis of transcription factor binding sites in human promoters. Genome Biol 13: R50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Diffner E, Beck D, Gudgin E, Thoms JA, Knezevic K, et al. (2013) Activity of a heptad of transcription factors is associated with stem cell programs and clinical outcome in acute myeloid leukemia. Blood 121: 2289–300. [DOI] [PubMed] [Google Scholar]
- 47. Chute JP, Ross JR, McDonnell DP (2010) Minireview: Nuclear receptors, hematopoiesis, and stem cells. Mol Endocrinol 24: 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Henke BR, Blanchard SG, Brackeen MF, Brown KK, Cobb JE, et al. (1998) N-(2-benzoylphenyl)-l-tyrosine ppargamma agonists. 1. discovery of a novel series of potent antihyperglycemic and antihyperlipidemic agents. J Med Chem 41: 5020–36. [DOI] [PubMed] [Google Scholar]
- 49. Brown KK, Henke BR, Blanchard SG, Cobb JE, Mook R, et al. (1999) A novel n-aryl tyrosine activator of peroxisome proliferator-activated receptor-gamma reverses the diabetic phenotype of the zucker diabetic fatty rat. Diabetes 48: 1415–24. [DOI] [PubMed] [Google Scholar]
- 50. Liebermann DA, Gregory B, Hoffman B (1998) Ap-1 (fos/jun) transcription factors in hematopoietic differentiation and apoptosis. Int J Oncol 12: 685–700. [DOI] [PubMed] [Google Scholar]
- 51. Shen LJ, Chen FY, Zhang Y, Cao LF, Kuang Y, et al. (2013) Mycn transgenic zebrafish model with the characterization of acute myeloid leukemia and altered hematopoiesis. PLoS One 8: e59070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Yu S, Jing X, Colgan JD, Zhao DM, Xue HH (2012) Targeting tetramer-forming gabpbeta isoforms impairs self-renewal of hematopoietic and leukemic stem cells. Cell Stem Cell 11: 207–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ghiaur G, Yegnasubramanian S, Perkins B, Gucwa JL, Gerber JM, et al.. (2013) Regulation of human hematopoietic stem cell self-renewal by the microenvironment’s control of retinoic acid signaling. Proc Natl Acad Sci U S A. [DOI] [PMC free article] [PubMed]
- 54. Okada S, Fukuda T, Inada K, Tokuhisa T (1999) Prolonged expression of c-fos suppresses cell cycle entry of dormant hematopoietic stem cells. Blood 93: 816–25. [PubMed] [Google Scholar]
- 55. Wozniak RJ, Keles S, Lugus JJ, Young KH, Boyer ME, et al. (2008) Molecular hallmarks of endogenous chromatin complexes containing master regulators of hematopoiesis. Mol Cell Biol 28: 6681–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Ziller MJ, Gu H, Muller F, Donaghey J, Tsai LT, et al. (2013) Charting a dynamic dna methylation landscape of the human genome. Nature 500: 477–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Kawana M, Lee ME, Quertermous EE, Quertermous T (1995) Cooperative interaction of gata-2 and ap1 regulates transcription of the endothelin-1 gene. Mol Cell Biol 15: 4225–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Zhang P, Behre G, Pan J, Iwama A, Wara-Aswapati N, et al. (1999) Negative cross-talk between hematopoietic regulators: Gata proteins repress pu.1. Proc Natl Acad Sci U S A 96: 8705–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Peixoto A, Monteiro M, Rocha B, Veiga-Fernandes H (2004) Quantification of multiple gene expression in individual cells. Genome Res 14: 1938–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Warren L, Bryder D, Weissman IL, Quake SR (2006) Transcription factor profiling in individual hematopoietic progenitors by digital rt-pcr. Proc Natl Acad Sci U S A 103: 17807–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Shalek AK, Satija R, Adiconis X, Gertner RS, Gaublomme JT, et al. (2013) Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells. Nature 498: 236–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Langmead B, Trapnell C, Pop M, Salzberg SL (2009) Ultrafast and memory-efficient alignment of short dna sequences to the human genome. Genome Biol 10: R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Miranda-Saavedra D, De S, Trotter MW, Teichmann SA, Gottgens B (2009) Bloodexpress: a database of gene expression in mouse haematopoiesis. Nucleic Acids Res 37: D873–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Hu ZL, Bao J, Reecy J (2008) Categorizer: A web-based program to batch analyze gene ontology classification categories. Online J Bioinform 9: 108–12. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Correlation analysis of gene expression levels measured using RNA-seq assays. (A) Reproducibility based on triplicate analyses of LT- and ST-HSCs. (B) Comparison of the gene expression correlations in the present study to those reported by Karlsson et al. [15], who purified HSCs using CD48−, CD150+, CD34−, CD9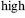 KSL for LT-HSCs and CD48−, CD150+, CD9
KSL for LT-HSCs and CD48−, CD150+, CD9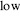 KSL for ST-HSCs.
KSL for ST-HSCs.
(EPS)
Contribution of higher-order TF interaction scores estimated by LLM. (A) Statistical differences of 2 regression coefficient (RC) ensembles of a TFBS found commonly by TGAS III and V (two-sample t-test). (B) Distribution of the TF interaction score 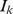 in Equation 9.
in Equation 9.
(EPS)
Box plots of RCs estimated by 100 iterations of regression modeling with TGAS V. Pos and Neg represent the positive (red) and negative (blue) mean values of RCs (red line), respectively.
(EPS)
Subnetworks involved in ST-HSC regulation. Although the majority of TF-coding genes found in ST-HSCs (Figure 4A) were not differentially expressed, 26 differentially expressed TFs that putatively bind to 21 TFBSs were present among DEGs (Class A and Class B).
(EPS)
Propensity of the TFBS activities inferred from public RNA-seq datasets. We applied our method to public RNA-seq datasets related to sequential cell development (A) and lineage commitment (C). Our procedure evaluates the averaged R of 5-fold CV on testing datasets (blue line). If a model improved R in testing, the model was accepted and its R value between the observed and predicted gene expression of all genes was measured (red line). (B) Of 147 TFBSs (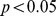 ), 67 TFBSs (Class A; upregulated in Oo) and 80 TFBSs (Class B; upregulated in 2C) exhibited significant gains and losses of activity (
), 67 TFBSs (Class A; upregulated in Oo) and 80 TFBSs (Class B; upregulated in 2C) exhibited significant gains and losses of activity (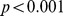 ). In addition, 73% (49/67) of Class A and 52.5% (42/80) of Class B genes exhibited no changes in the effects of their TFBS activities between cells, i.e., positive (negative) in Oo was still positive (negative) in 2C. We found that 16% (8/49) of Class A and 83% (35/42) of Class B genes had increased activities in 2C compared with Oo. (D) Among 150 TFBSs (
). In addition, 73% (49/67) of Class A and 52.5% (42/80) of Class B genes exhibited no changes in the effects of their TFBS activities between cells, i.e., positive (negative) in Oo was still positive (negative) in 2C. We found that 16% (8/49) of Class A and 83% (35/42) of Class B genes had increased activities in 2C compared with Oo. (D) Among 150 TFBSs (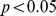 ), 98 TFBSs (Class A, upregulated in MEP) and 114 TFBSs (Class B, upregulated in Mk) exhibited significant gains and losses of activity (
), 98 TFBSs (Class A, upregulated in MEP) and 114 TFBSs (Class B, upregulated in Mk) exhibited significant gains and losses of activity (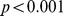 ). We also found that 83% (81/98) of Class A and 76% (87/114) of Class B genes exhibited no changes in the effects of their TFBS activities. All of the TFBSs in both classes exhibited increases in the strengths of their activities in Mk compared with MEP. R, Pearson's correlation coefficient; Oo, MII oocytes; 2C, 2-cell embryo; MEP, megakaryocyte/erythroid precursor; Mk, megakaryocyte.
). We also found that 83% (81/98) of Class A and 76% (87/114) of Class B genes exhibited no changes in the effects of their TFBS activities. All of the TFBSs in both classes exhibited increases in the strengths of their activities in Mk compared with MEP. R, Pearson's correlation coefficient; Oo, MII oocytes; 2C, 2-cell embryo; MEP, megakaryocyte/erythroid precursor; Mk, megakaryocyte.
(EPS)
RNA-seq mapping statistics.
(XLSX)
Differentially expressed cell-surface molecules.
(XLSX)
Differentially expressed transcription factors.
(XLSX)
Transcription factors categorized into Class C.
(XLSX)
Low expressed transcription factors (Class D).
(XLSX)
Average regression coefficient of 142 TFBSs.
(XLSX)
Classification of MkE, GM, and Lymphoid-associated genes.
(XLSX)
TFBSs significantly different in the regression coefficient between LT- and ST-HSCs (Class A).
(XLSX)
TFBSs significantly different in the regression coefficient between LT- and ST-HSCs (Class B).
(XLSX)
Enriched GO terms in Class A.
(XLSX)
Enriched GO terms in Class B.
(XLSX)
Result of log-linear model in Class A.
(XLSX)
Result of log-linear model in Class B.
(XLSX)