Accounting for selection bias in association studies with complex survey data

Abstract

Obtaining representative information from hidden and hard-to-reach populations is fundamental to describing the epidemiology of many sexually transmitted diseases, including HIV. Unfortunately simple random sampling is impractical in these settings, as no registry of names exists from which to sample the population at random. However, complex sampling designs can be used as members of these populations tend to congregate at known locations, which can be enumerated and sampled at random. For example, female sex workers may be found at brothels and street corners, whereas injection drug users often come together at shooting galleries. Despite the logistical appeal, complex sampling schemes lead to unequal probabilities of selection, and failure to account for this differential selection can result in biased estimates of population averages and relative risks. However, standard techniques to account for selection can lead to substantial losses in efficiency. Consequently, researchers implement a variety of strategies in an effort to balance validity and efficiency. Some fully or partially account for the survey design, while others do nothing and treat the sample as a realization of the population of interest. We use directed acyclic graphs to show how certain survey sampling designs, combined with subject-matter considerations unique to individual exposure-outcome associations, can induce selection bias. Finally, we present a novel yet simple maximum likelihood approach for analyzing complex survey data, which optimizes statistical efficiency at no cost to validity. We use simulated data to illustrate this method and compare it with other analytic techniques.

Obtaining representative information from hidden and hard-to-reach populations is fundamental to epidemiologic description of sexually transmitted diseases. Members of these populations often contribute disproportionately to transmission. For example, female sex workers often act as reservoirs of infection from which HIV spreads to the general population through their male clients.^1–4 Unfortunately, simple random sampling of such persons is difficult and impractical. There are no lists of names from which to sample the population at random. Even if such a registry existed, these groups are small proportions of the population, making it unlikely that random sampling would capture enough people for sub-group analyses. Finally, these populations often conceal themselves because their activities are illegal or highly stigmatized. Persons who can be reliably identified by traditional sampling approaches may differ in important ways from those who cannot.

Complex sampling has been used successfully to obtain representative samples of hidden and hard-to-reach populations.^5–8 This type of sampling differs from simple random sampling in that the primary sampling unit is a group of persons, rather than a single person. Groups are first enumerated and then the specific groups to be sampled are selected at random. Then, within the selected groups, individuals are sampled into the survey. Complex sampling can be effective at capturing hard-to-reach populations because members tend to congregate at known locations. For example, female sex workers may be found at brothels and street corners, whereas drug users often come together at shooting galleries. The gathering locations serve as “clusters” from which individuals can be selected for participation.

Although complex sampling has logistical appeal, it presents analytic challenges. The sampling framework leads to an unequal probability of selection across individuals and thus to potentially biased estimates of population averages. Although it is standard practice to weight each person by the inverse of the probability of selection in order to estimate population averages, it is unclear what adjustment, if any, should be made in regression analyses.^9,10 Some complex surveys recommend incorporating the sampling weights in every analysis, ^11–13 while others explicitly instruct users to disregard sampling weights when estimating regression coefficients.¹⁷ In practice, researchers accessing the same data may implement a variety of adjustment strategies; some fully or partially account for the unequal selection,¹⁴ while others treat the sample as the population of interest.¹⁵

We use directed acyclic graphs (DAGs) to demonstrate how certain sampling designs, combined with subject-matter considerations unique to individual exposure-outcome associations, can induce selection bias. DAGs provide an intuitive framework to formally encode subject-matter knowledge about underlying relationships in the observed data.^16,17 Simple graphical rules can be applied to DAGs to identify potential problems with different analytic strategies. We present and explore the implications for bias for six structures generated by the variables exposure A, outcome Y, confounder L, selection into the sample S, and determinants of selection M, N, and O. Next we review the appropriateness of two common techniques that adjust for the sampling design of complex surveys – unweighted regression conditional on determinants of selection and weighted unconditional regression. We also develop a maximum likelihood approach that appropriately accounts for the sampling design and that resolves well-known limitations of existing analytic techniques. Finally, we use simulation to illustrate and compare the likelihood approach with other methods.

DIRECTED ACYCLIC GRAPHS

For each structure presented in the figures, we provide examples based on a publically-available, complex survey: Integrated Behavioral and Biological Assessment. In 2003, with the support of the Indian government, the Bill and Melinda Gates Foundation provided funding for the Avahan India AIDS Initiative. Avahan delivers HIV prevention services to more than 80% of high-risk persons in the six states that account for the majority of all HIV infections in the country.¹⁸ The survey was commissioned to evaluate Avahan’s impact on pre-specified behavioral and biological indicators among its target populations. We have chosen to focus on the survey carried out among female sex workers.

The Indian survey used a complex sampling strategy to identify and select respondents.⁵ Within each state, districts were selected to achieve the highest concentrations of high-risk persons across a diverse range of cultural and ethnographic characteristics. Within each chosen district, locations were selected with probability proportional to the expected number of potentially eligible respondents. For female sex workers operating in brothels, home, lodges and road-side eating establishments, individuals were enumerated at each chosen location and then randomly selected for inclusion in the study. Street-based female sex workers were enumerated based on location, day of the week or weekend, and hour(s) of the day (i.e. time-location sampling) and then randomly selected. As a result of this sampling design, selection into the survey sample of female sex workers depends on location of solicitation, day/time of solicitation, and district.

Before proceeding, we note that we ignore potential clustering of responses among survey participants. Assumptions regarding intraclass correlation relate only to obtaining appropriate standard errors, whereas not appropriately accounting for the survey’s design may induce bias. Thus, we assume no intraclass correlation and instead focus on the impact of the survey’s design characteristics on potential bias in the point estimates only. Furthermore, we have drawn all DAGs under the null hypothesis of no effect of the exposure on the outcome, conditional on a set of measured confounding factors; this hypothesis may or may not hold in the given analysis. Finally, the target parameter is the odds-ratio association between risk factors and an outcome in the underlying population. Therefore, we do not require that the DAGs be causal DAGs.

Determinants of selection affect exposure and outcome

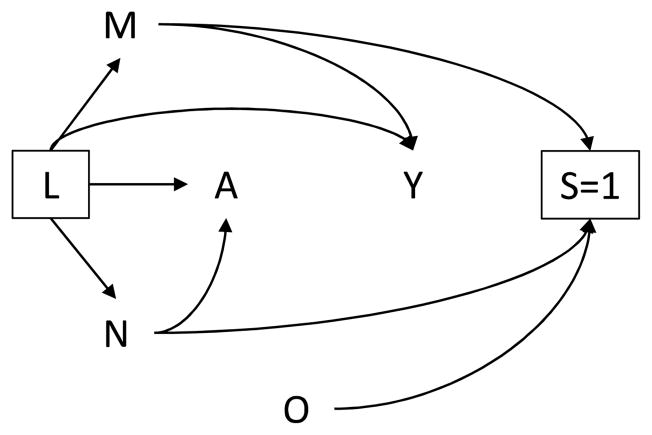
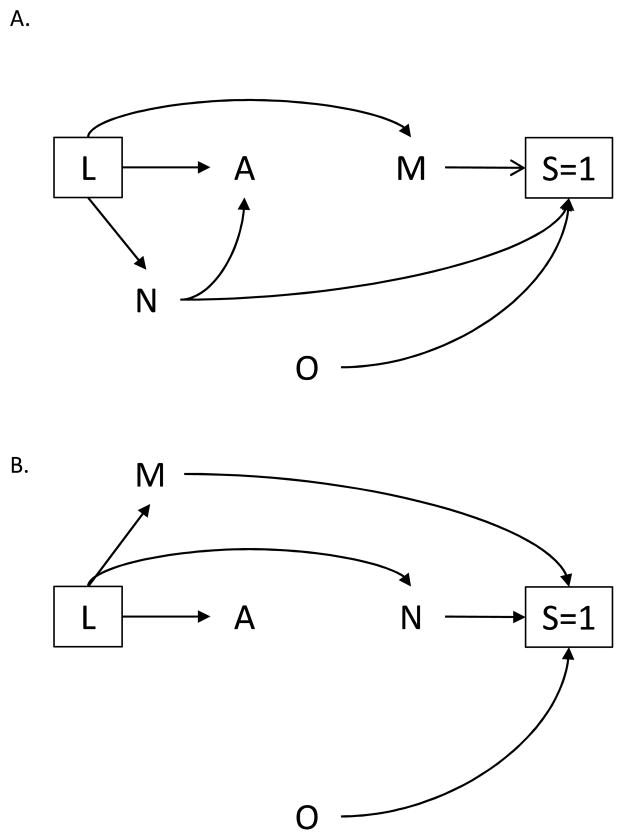
Figure 1 represents a cross-sectional analysis examining the relationship between the number of clients entertained per day A and HIV infection Y, using survey data collected among adult female sex workers. Recall that the variable S indicates whether a woman is selected for participation in the survey. The square around the variable S indicates that the analysis is restricted to women who participated in the survey (S=1). Likewise, the square around the variable L indicates that all analyses are conducted within levels of confounders L. The arrows from M, N, and O to S, and the lack of an arrow into S, indicate that the survey’s complex sampling framework was determined by location of solicitation M, day/time of solicitation N, and district O.

Figure 1.

Directed acyclic graph in which the determinants of selection M and N are associated with exposure A and outcome Y.

The arrow from M to Y in Figure 1 may be due to higher HIV prevalence among female sex workers operating at brothels compared with other locations. Additionally, the arrow from N to A is present because women who solicit sex on weekends or during the evening hours may entertain larger numbers of clients per day compared with women who solicit sex on weekdays or during daylight hours. Crude analyses will generally yield an association between A and Y in the survey sample even if A and Y were conditionally independent given a set of measured confounders L in the population. This type of bias, an instance of so-called “collider bias”, can occur when one selects or conditions on a variable that is itself affected (either directly or through intermediate factors) by exposure and outcome. In this setting, exposure and outcome, even if marginally independent, will be associated within levels of the selection or conditioning variable.^19–22 Here, selection into the survey sample is a collider for the variables M and N. Conditioning on selection (S=1) creates an association between exposure (A) and outcome (Y) in the survey sample not present in the population.

One determinant of selection affects exposure or outcome, but not both

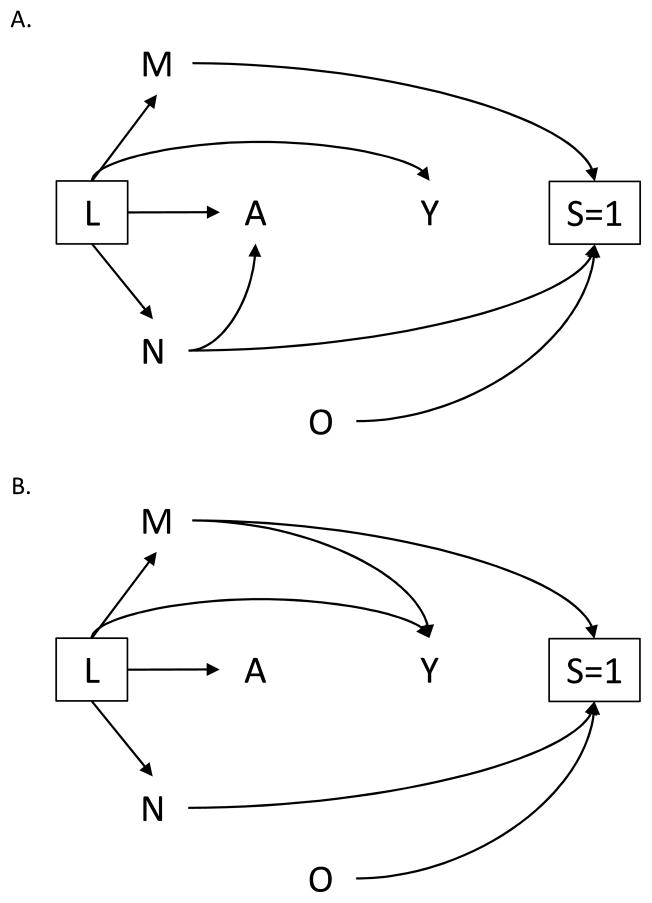
Suppose another investigator examines the relationship between the number of clients entertained daily A and sexual violence Y rather than HIV infection. Figure 2A. depicts the structure for this new study. The investigator retains the arrow from N to A representing the association between day/time of solicitation and client volume. However, she removes the arrow from M to Y based on her subject-matter knowledge that location of solicitation has no direct effect on sexual violence. Unlike the previous study, under the null hypothesis and conditional on the set of measured confounders L, exposure and outcome remain marginally independent in the survey sample. That is, contrasts of risks will be unbiased even if one does not adjust for M or N.

Figure 2.

Directed acyclic graph in which one determinant of selection M or N, but not both, is associated with (A.) exposure A or (B.) outcome Y, conditional on L.

Alternatively, suppose the first investigator decided to examine the effect of lack of formal education A (instead of number of clients entertained daily) on HIV infection Y. An empirical assessment of the Indian survey data suggests no association between day/time of solicitation and the new exposure. If that were indeed the case, the investigator would remove the arrow from N to A to represent this additional information in the updated DAG depicted by Figure 2B. Similar to the second investigator’s study (Figure 2A.), no additional adjustment for selection would be required for unbiased contrasts in risks conditional on the set of measured confounders L.

No determinant of selection affects exposure or outcome

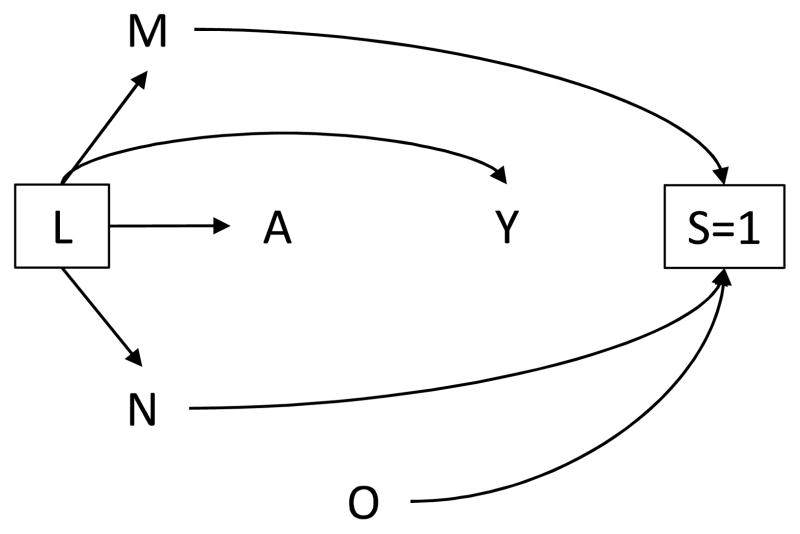
Suppose a third investigator examines the association between lack of formal education A and history of sexual violence Y. The resulting DAG (Figure 3) does not contain arrows from M to Y or from N to A, reflecting his subject matter knowledge that neither determinant of selection is associated with the exposure or outcome. Therefore, the unequal probability of selection induced by the sampling design does not result in selection bias for inferences about the joint distribution of A and Y conditional on L. Assuming no intraclass correlation for subjects within the same cluster, these data can be treated as if obtained via simple random sampling.

Figure 3.

Directed acyclic graph in which no determinant of selection M, N is associated with exposure A or outcome Y.

A determinant of selection is the exposure of interest

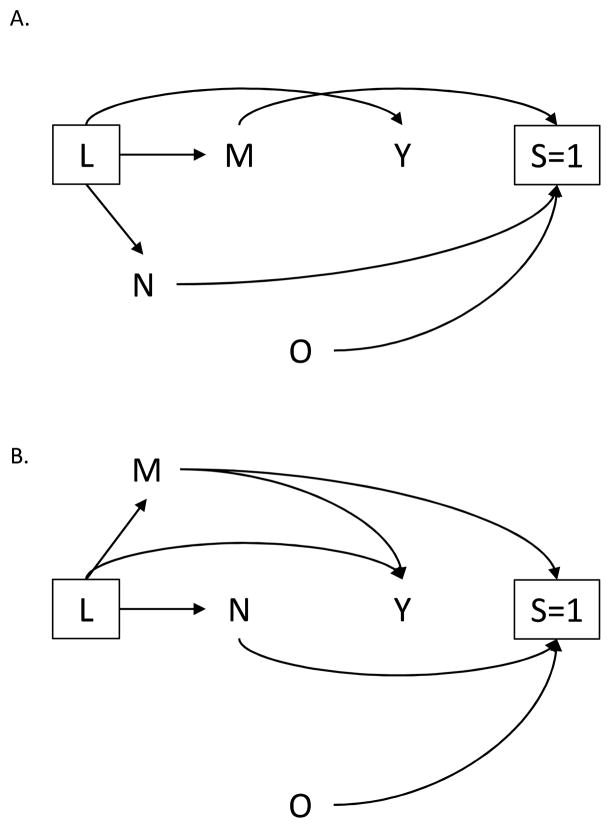
A determinant of selection may itself be of interest as an exposure under study. For example, brothel-based sex workers in India may be more likely to join sex-worker collectives that seek to empower and unite sex workers, which may in turn lead to increased condom use. Therefore, an investigator may wish to examine the relationship between location of solicitation M and condom use Y. As depicted in Figure 4A., the sampling scheme does not induce bias, as location of solicitation and condom use remain independent under the null hypothesis. However, if the investigator alternatively considered day/time of solicitation as the exposure of interest, a crude analysis would yield biased effect estimates (Figure 4B.), even after conditioning on the set of measured confounders L.

Figure 4.

Directed acyclic graph in which one determinant of selection, (A.) M or (B.) N, is the exposure of interest.

A determinant of selection is the outcome of interest

Alternatively, a determinant of selection itself may be of interest as the outcome under study. Previous studies of female sex workers have reported that women who solicit sex from brothels may be at higher risk for HIV.²³ Identifying determinants of brothel-based sex work or correlates of day/time of solicitation may inform local HIV prevention programming. Thus, the investigator may also be interested in M (Figure 5A.) or N (Figure 5B.) as the outcome. In Figure 5A., failure to account for the complex sampling design will result in biased estimates of the relationship between A and M conditional on L, because survey participation (S=1) is a downstream consequence of exposure (A) and location of solicitation (M). Restricting the analysis to those women who participated in the ssurvey, would generally produce non-null findings, even under the null hypothesis,

Figure 5.

Directed acyclic graph in which one determinant of selection, (A.) M or (B.), N is the outcome of interest.

A determinant of selection is both the exposure and outcome of interest

Finally, determinants of selection may be of interest as the exposure and outcome under study. Figure 6 presents the corresponding DAG. In this setting, similar to Figure 5A., the sampling design induces selection bias because survey participation is a direct downstream consequence of both exposure (M) and outcome (N).

Figure 6.

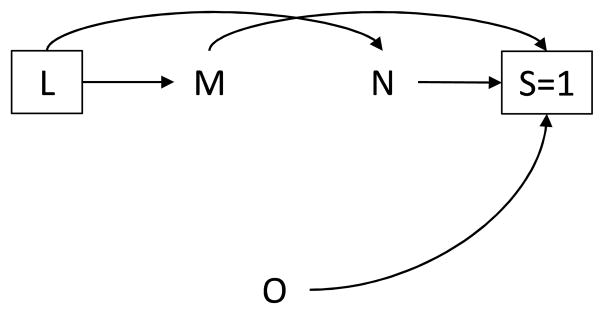
Directed acyclic graph in which the determinants of selection, M and N, are the exposure and outcome of interest, respectively.

ADJUSTMENT FOR SELECTION BIAS INDUCED BY COMPLEX SAMPLING

In the DAGs depicted in Figures 1, 4B, 5A and 6, unadjusted contrasts of risk are not expected to result in unbiased effect estimates. Multiple methods have been proposed to adjust for selection bias induced by complex survey sampling, including unweighted regression conditional on determinants of selection and weighted unconditional regression.^9,24,25 We review the appropriateness of these approaches before introducing a third technique based on the observed data likelihood function.

Unweighted conditional regression

In unweighted conditional regression, all determinants of selection are included as covariates. This yields an unbiased conditional effect estimate assuming M, N, and O are recorded and the regression model is correctly specified. In practice, meeting these two requirements can be difficult. Correct model specification requires that all nonlinearities and higher-order interactions involving M, N, and O, must be included in the model. Yet, as the number of covariates needed to properly adjust for selection grows, the method becomes increasingly challenging. Therefore, some recommend a compromise that includes some, but not all, determinants of selection in the model.¹⁴ This approach may alleviate efficiency concerns, but potentially at the cost of bias.

The appropriateness of the no-model-misspecification assumption depends on direct knowledge of the survey’s sampling design in order to identify all determinants of selection. Most complex surveys provide sampling probabilities, but the factors used to determine these probabilities are not always recorded in the distributed files. For example, while information on location of solicitation is available for all female sex workers participating in the Indian survey, the data file distributed to external investigators does not include the day/time of solicitation for women selected via time-location sampling. Adjustment using unweighted conditional regression in this setting is unlikely to yield unbiased effect measures.

Weighted unconditional regression

Weighted unconditional regression weights each subject by the inverse of the probability of selection (i.e Horvitz-Thompson type estimator)²⁶ in order to adjust for the selection bias introduced by complex sampling. In the weighted population, selection does not depend on any covariates. The data can be treated as if obtained by simple random sampling because, for example in the case of the Indian survey, the joint distribution of M, N, A, L, and O in the weighted population is identical to that observed in the population. Therefore, a crude analysis in the weighted population will result in unbiased population averages and relative risks.

Maximum likelihood

An important limitation of both methods is loss of efficiency. As the distribution of the sampling weights becomes more variable, weighted regression may also become increasingly inefficient. Conditioning on determinants of selection has the additional, and perhaps more troublesome, limitation of model misspecification, resulting in biased effect estimates. We present a third approach based on the observed data likelihood under selection that optimizes statistical efficiency at no cost to validity.

eAppendix A provides the likelihood functions for each DAG. Here, we give the likelihood for the canonical case depicted in Figure 6 in which two determinants of selection, M and N, are the exposure and outcome of interest, respectively. We derive a person’s contribution to the likelihood without necessarily assuming that the null hypothesis holds, as depicted in Figure 6. Let

$$\mathit{logit}\left[P[N=1\mid M,L]\right]=\alpha +{\beta }_{1}M+{\beta }_{2}L$$ (1)

denote the correctly-specified regression model in the population, where N is taken to be binary. Therefore, β₁ is interpreted as the log odds ratio of N comparing persons who were and were not exposed to M conditional on L in the population.

To construct the likelihood, consider the conditional event probability of N given M, L, and S=1, obtained via Bayes Theorem

$$P[N=1\mid M,L,S=1]=\frac{P[S=1\mid M,N,L]P[N\mid M,L]}{{\sum }_{j=0,1}P[S=1\mid M,N=j,L]P[N=j\mid M,L]}$$ (2)

We observe that P[S = 1 |M, N, L] is exactly equal to the final sampling probability, τ(M, N, L), which is estimated using the survey’s sampling design. We assume access to the individual-level information used to compute τ(M, N, L), but the approach may still be implemented if only a coarsening of this information is available (e.g. based on advance impressions, previous research, or expert opinion). Then, under the logistic regression model (1), one obtains

$$P[N=1\mid M,L,S=1]=\frac{\tau (M,N,L)\left[\frac{e^{\{N(\alpha +{\beta }_{1}M+{\beta }_{2}L)\}}}{1+e^{\{\alpha +{\beta }_{1}M+{\beta }_{2}L\}}}\right]}{{\sum }_{j=0,1}\tau (M,N=j,L)\left[\frac{e^{\{j(\alpha +{\beta }_{1}M+{\beta }_{2}L)\}}}{1+e^{\{\alpha +{\beta }_{1}M+{\beta }_{2}L\}}}\right]}$$ (3)

Simplification of (3) leads to the expression

$$\mathit{logit}\left[P[N=1\mid M,L,S=1]\right]=\mathit{log}\left[\frac{\tau (M,N=1,L)}{\tau (M,N=0,L)}\right]+\alpha +{\beta }_{1}M+{\beta }_{2}L$$ (4)

where β₁ represents the effect of interest and, as we explain below, the offset term, $\mathit{log}\left[\frac{\tau (M,N=1,L)}{\tau (M,N=0,L)}\right]$, quantifies the selection bias introduced by the survey’s complex sampling strategy. Let $g(M)=\mathit{log}\left[\frac{\tau (M,N=1,L)}{\tau (M,N=0,L)}\right]$ and, because M is binary, g(M) = g(0) + [g(1) − g(0)]M. Suppose we ignore the offset term in (4) and instead fit the following model

$$\mathit{logit}\left[P[N=1\mid M,L,S=1]\right]={\alpha }^{\ast }+{{\beta }_1}^{\ast }M+{{\beta }_2}^{\ast }L$$ (5)

Even though (5) is a correctly-specified logistic regression equation in the survey sample, it follows from g(M) that β₁^* = β₁ + [g(1) − g(0)] and therefore β₁^* does not generally equal β₁. The measures are guaranteed to coincide only if g(1) = g(0) or selection into the sample is independent of M. Similarly, the model in (5) cannot be used for prediction because the intercept α^* does not equal α; rather, α^* = α + g(0). This last expression is an immediate consequence of the fact that selection into the sample depends on the outcome N.

SIMULATIONS

To illustrate the likelihood approach and compare it with existing analytic methods, we simulated data based on the DAG depicted in Figure 6. We generated exposure M as a uniformly distributed random variable (n=40,000). Next, we generated L by drawing from a standard normal distribution, before evenly dividing M into three non-overlapping groups, and defining the following individual risk model:

$$\mathit{logit}\left[P[N=1\mid M,L]\right]=\alpha +{\beta }_1{M}_1+{\beta }_2{M}_2+{\beta }_{3}L$$ (6)

We generated the binary variables N and O by drawing from a Bernoulli distribution under (6) and 0.25 (respectively) before selecting a 1% sub-sample with unequal probability of selection according to M, N, and O. Table 1 presents the selection probabilities used to oversample individuals with {M = 3, N = 0, O = 0}, {M = 1, N = 0, O = 0}, or {M = 1, N = 1, O = 1}, thereby inducing an association between selection (S = 1), exposure (M), and outcome (N).

Table 1.

Probability of selection into the 1% sub-sample according to M, N, and O.

	O = 0			O = 1
	N = 0	N = 1		N = 0	N = 1
M1: M = 1	0.2	0.1	M1: M = 1	0.05	0.15
M2: M = 2	0.01	0.05	M2: M = 2	0.0025	0.075
M3: M = 3	0.19	0.05	M3: M = 3	0.0475	0.075

We first fit a logistic regression model that accounts for confounding by the variable L but ignores the sampling design. For the unweighted conditional regression models, we added the determinant of selection O to the model, whereas in the weighted unconditional approach we weighted each participant by the inverse of the probability of selection into the survey sample.

We compared the performance of each method in addition to no adjustment under eight model specifications defined by β₁, β₂, and β₃. Specifically, we simulated all eight combinations between weak and strong exposure effects (β₁ = 0.1, β₂ = 0.4 and β₁ = 0.4, β₂ = 0.8, respectively); weak and strong confounding effects (β₃ = 0.4 and β₃ = 0.8, respectively); and weak and strong exposure-confounder associations (OR_E–C = 1.1 and (OR_E–C = 1.6, respectively). All scenarios assumed a marginal disease prevalence of 2%. We calculated the absolute bias, Monte Carlo and empirical standard errors, and root mean squared error across 1,000 simulations, each with a sample size of 400.

Simulation results

Table 2 summarizes the absolute bias and root mean squared error observed across the eight simulation scenarios for unadjusted and adjusted models. Analyses that ignored the sampling design completely or in part resulted in upwardly biased parameter estimates. Compared with no adjustment, conditioning on the determinant of selection O decreased bias in the intercept slightly, but had no impact in the amount of bias observed for the effects of exposure (β₁, β₂).

Table 2.

Bias (root mean squared error) in a 1% sub-sample (n=400) under various population models with and without adjustment for selection into the sub-sample

	Weak exposure effecta Weak confounding effectc				Weak exposure effecta Strong confounding effectd				Strong exposure effectb Weak confounding effectc				Strong exposure effectb Strong confounding effectd
	α	β1	β2	β3	α	β1	β2	β3	α	β1	β2	β3	α	β1	β2	β3
Weak association between confounder and exposuree
Unadjusted	3.18 (3.18)	0.50 (0.51)	2.56 (2.56)	0.01 (0.01)	2.96 (2.97)	0.47 (0.48)	2.57 (2.57)	0.01 (0.13)	3.18 (3.18)	0.41 (0.41)	2.15 (2.15)	0.00 (0.11)	2.96 (2.96)	0.37 (0.38)	2.17 (2.7)	0.01 (0.13)
Unweighted conditional regression	2.48 (2.48)	0.50 (0.51)	2.56 (2.56)	0.01 (0.12)	2.56 (2.26)	0.47 (0.48)	2.57 (2.58)	0.02 (0.14)	2.48 (2.48)	0.41 (0.41)	2.15 (2.16)	0.01 (0.12)	2.26 (2.26)	0.37 (0.38)	2.17 (2.18)	0.01 (0.14)
Weighted unconditional regression	−0.06 (0.16)	−0.01 (0.12)	0.14 (0.35)	0.07 (0.28)	−0.12 (0.29)	−0.02 (0.18)	0.23 (0.55)	0.14 (0.33)	−0.07 (0.18)	0.00 (0.12)	0.15 (0.35)	0.07 (0.32)	−0.15 (0.34)	0.00 (0.19)	0.25 (0.60)	0.14 (0.38)
Likelihood	−0.01 (0.08)	0.00 (0.10)	0.01 (0.12)	0.01 (0.12)	−0.01 (0.11)	0.00 (0.12)	0.02 (0.18)	0.01 (0.13)	−0.01 (0.08)	0.01 (0.10)	0.01 (0.11)	0.01 (0.12)	−0.01 (0.11)	0.01 (0.12)	0.01 (0.18)	0.01 (0.13)
Strong association between confounder and exposuref
Unadjusted	3.17 (1.95)	0.35 (0.10)	2.56 (2.92)	0.01 (0.04)	2.95 (2.95)	0.17 (0.20)	2.56 (2.57)	0.02 (0.13)	3.18 (3.18)	0.26 (0.26)	2.16 (2.16)	0.01 (0.12)	2.95 (2.95)	0.08 (0.13)	2.18 (2.18)	0.02 (0.12)
Unweighted conditional regression	2.48 (1.89)	0.35 (0.10)	2.56 (0.09)	0.01 (0.04)	2.25 (2.25)	0.17 (0.20)	2.57 (2.57)	0.02 (0.14)	2.48 (2.48)	0.26 (0.26)	2.16 (2.16)	0.01 (0.13)	2.25 (2.25)	0.08 (0.13)	2.18 (2.18)	0.02 (0.13)
Weighted unconditional regression	−0.06 (0.06)	−0.03 (0.09)	0.14 (0.31)	0.07 (0.06)	−0.12 (0.26)	−0.04 (0.20)	0.21 (0.54)	0.12 (0.31)	−0.08 (0.19)	−0.03 (0.18)	0.16 (0.28)	0.09 (0.32)	−0.15 (0.32)	−0.05 (0.23)	0.24 (0.58)	0.15 (0.35)
Likelihood	−0.01 (0.06)	0.00 (0.08)	0.01 (0.12)	0.01 (0.04)	−0.02 (0.11)	0.00 (0.13)	0.02 (0.18)	0.02 (0.13)	−0.01 (0.08)	0.00 (0.11)	0.01 (0.12)	0.01 (0.13)	−0.02 (0.11)	0.00 (0.13)	0.01 (0.17)	0.02 (0.13)

Note: All scenarios simulated under a disease prevalence of 2 percent (α=−3.9) and the following population model: logit[P[N = 1|M, L]] = α + β₁M₁ + β₂M₂ +β₃L

^aWeak exposure effect defined as β₁= 0.1 and β₂= 0.4

^bStrong exposure effect defined as β₁= 0.2 and β₂= 0.8

^cWeak confounding effect defined as β₃= 0.4

^dStrong confounding effect defined as β₃= 0.8

^eWeak association between confounder and exposure defined as OR_C-E= 1.1

^fStrong association between confounder and exposure defined as OR_C-E= 1.6

In contrast, both approaches that fully incorporated the sampling design resulted in minimal to no bias. For all parameters across all scenarios, maximum likelihood produced unbiased effect estimates; the weighted approach resulted in a slight bias throughout. The magnitude of the bias observed with weighting tended to increase with strong confounding, irrespective of the strength of the exposure-confounder association. Conversely, the strength of the exposure effect did not appear to influence the amount of bias produced by weighted regression.

We found a similar pattern for the Monte Carlo and empirical standard errors across the four approaches (Table 3). As predicted by theory (see Appendix), the likelihood approach was more efficient than the weighted unconditional regression. The empirical standard errors closely matched the Monte Carlo standard errors in all scenarios, except in the setting of weak exposure and confounding effects coupled with a strong association between the confounder and exposure. In all methods, the empirical standard errors underestimated the Monte Carlo standard errors.

Table 3.

Monte Carlo standard error (empirical standard error^a) in a 1% sub-sample (n=400) under various population models with and without adjustment for selection into the sub-sample

	Weak exposure effectb Weak confounding effectd				Weak exposure effectb Strong confounding effecte				Strong exposure effectc Weak confounding effectd				Strong exposure effectc Strong confounding effecte
	α	β1	β2	β3	α	β1	β2	β3	α	β1	β2	β3	α	β1	β2	β3
Weak association between confounder and exposuref
Unadjusted	0.04 (0.04)	0.05 (0.05)	0.07 (0.07)	0.11 (0.11)	0.09 (0.09)	0.09 (0.09)	0.15 (0.15)	0.13 (0.13)	0.05 (0.05)	0.05 (0.05)	0.07 (0.07)	0.11 (0.11)	0.09 (0.09)	0.09 (0.09)	0.15 (0.15)	0.13 (0.13)
Unweighted conditional regression	0.05 (0.05)	0.05 (0.05)	0.08 (0.08)	0.12 (0.12)	0.10 (0.10)	0.09 (0.09)	0.17 (0.17)	0.14 (0.14)	0.06 (0.06)	0.05 (0.05)	0.09 (0.09)	0.12 (0.12)	0.11 (0.11)	0.09 (0.09)	0.17 (0.17)	0.14 (0.14)
Weighted unconditional regression	0.15 (0.15)	0.12 (0.12)	0.32 (0.32)	0.27 (0.27)	0.26 (0.26)	0.18 (0.18)	0.51 (0.50)	0.30 (0.30)	0.16 (0.16)	0.12 (0.12)	0.31 (0.31)	0.31 (0.31)	0.30 (0.30)	0.19 (0.19)	0.55 (0.55)	0.35 (0.35)
Likelihood	0.08 (0.08)	0.10 (0.10)	0.11 (0.11)	0.12 (0.12)	0.11 (0.11)	0.12 (0.12)	0.18 (0.18)	0.13 (0.13)	0.08 (0.08)	0.10 (0.10)	0.11 (0.11)	0.12 (0.12)	0.11 (0.11)	0.12 (0.12)	0.18 (0.18)	0.13 (0.13)
Strong association between confounder and exposureg
Unadjusted	0.05 (0.07)	0.06 (0.08)	0.08 (0.08)	0.12 (0.04)	0.09 (0.09)	0.10 (0.10)	0.15 (0.15)	0.13 (0.13)	0.05 (0.05)	0.07 (0.07)	0.08 (0.08)	0.12 (0.12)	0.09 (0.09)	0.10 (0.10)	0.15 (0.15)	0.12 (0.12)
Unweighted conditional regression	0.06 (0.07)	0.07 (0.08)	0.09 (0.08)	0.13 (0.04)	0.11 (0.11)	0.10 (0.10)	0.16 (0.16)	0.13 (0.13)	0.06 (0.06)	0.07 (0.07)	0.09 (0.09)	0.13 (0.13)	0.11 (0.11)	0.10 (0.10)	0.16 (0.16)	0.13 (0.13)
Weighted unconditional regression	0.15 (0.06)	0.16 (0.09)	0.31 (0.09)	0.26 (0.06)	0.24 (0.24)	0.20 (0.20)	0.50 (0.50)	0.28 (0.28)	0.18 (0.18)	0.18 (0.18)	0.34 (0.34)	0.31 (0.31)	0.29 (0.29)	0.22 (0.22)	0.53 (0.53)	0.32 (0.32)
Likelihood	0.08 (0.06)	0.11 (0.08)	0.12 (0.08)	0.13 (0.04)	0.11 (0.11)	0.13 (0.13)	0.18 (0.18)	0.13 (0.13)	0.08 (0.08)	0.11 (0.11)	0.12 (0.12)	0.13 (0.13)	0.11 (0.11)	0.13 (0.13)	0.17 (0.17)	0.13 (0.13)

Note: All scenarios simulated under a disease prevalence of 2 percent (α =−3.9) and the following population model: logit[P[N = 1|M, L]] = α + β₁M₁ + β₂M₂ +β₃L

^aEmpirical standard error calculated as the standard deviation of the estimate of interest from all simulations as $\sqrt{\left(1/(B-1)\right)\sum {\left({\widehat{\beta }}_i-\overline{\widehat{\beta }}\right)}^2}$ where B = number of simulations.

^bWeak exposure effect defined as β₁= 0.1 and β₂= 0.4

^cStrong exposure effect defined as β₁= 0.2 and β₂= 0.8

^dWeak confounding effect defined as β₃= 0.4

^eStrong confounding effect defined as β₃ = 0.8

^fWeak association between confounder and exposure defined as OR_C-E= 1.1

^gStrong association between confounder and exposure defined as OR_C-E= 1.6

DISCUSSION

It has been argued that, despite the unequal selection induced by the design of complex surveys, analyses that treat the sampled data as the population of interest remain valid. Using a DAG framework, we show that this will depend on knowledge about the relationships among determinants of selection, exposure, and outcome. If the determinants of selection are associated with exposure and outcome, failure to account for the sampling design may result in biased effect estimates. This includes settings where determinants of selection are the exposure or outcome under study.

Under these circumstances, there are multiple analytic options. Given our simulation findings, partial adjustment for selection by conditioning on determinants may only minimally improve bias compared with no adjustment; weighted regression will yield effect estimates that are much less biased, especially in the setting of weak confounding effects. Maximum likelihood naturally accounts for selection because it considers the sampling design as part of the underlying data-generating mechanism. It also has the distinct advantage of delineating the amount of bias introduced by the sampling design. Furthermore, it can readily be implemented in standard software. In the canonical scenario (Figure 6), the analyst needs to specify only the OFFSET option in PROC LOGISTIC in SAS (see eAppendix B). For more complicated DAGs, the likelihood approach can still be implemented using standard software packages, but may require the use of more sophisticated procedures including PROC NLMIXED. Additional perspectives on this problem – although not developed for use in complex survey samples – are provided by Bareinboim and Pearl²⁷ and Rose and Van der Laan.²⁸

The structural considerations discussed here are analogous to nested, matched case-control studies. As with complex surveys, the probability of selection for each participant in a matched, nested case-control study can be estimated, given the design. In such studies, cases are matched to controls according to one or more factors thought to be confounders. If the matching factor truly confounds the exposure-outcome relationship, then failing to account for matching will generally result in biased effect estimates.²⁹ However, even if the matching factor is not a common cause of exposure and outcome, bias can still result if the factor is correlated with exposure. This phenomenon, known as “overmatching,” results from conditioning on the common effect, selection into the study. In this situation, as in the DAGs presented in Figures 1, 4B., 5A. and 6, collider bias transforms the matching factors into confounders in the sample even if they are not confounders in the population.

Despite the use of probability-based sampling, members of the target population may be missed by complex surveys. In the Indian survey, female sex workers who cannot be associated with places and/or times of congregation (e.g. women who solicit sex via mobile telephones) are unlikely to have been sampled. Such undercoverage of the target population may lead to incorrect sampling probabilities and consequently may undermine efforts to obtain a representative sample. Our likelihood approach is vulnerable to this uncertainty, as it uses the sampling probabilities to construct the offset term. To our knowledge, undercoverage would affect all existing methods that attempt to respect the sampling design by incorporating the estimated sampling weights. It would be both interesting and important to work out methods that address this problem, but this is beyond the scope of the current paper. Briefly, a Bayesian framework that formally incorporated imperfect information about the sampling weights by positing a prior for such parameters based on information about the survey’s design could be used to produce a posterior for both the weights and regression parameters. Such an approach would build on the parameterization proposed here, and be a natural extension of our likelihood approach. Another appeal of working with the likelihood function is that, while the offset term may be misspecified due to an incorrect sampling weight, the maximum likelihood estimation remains well-defined as the minimizer of the Kullback-Leibler distance, a projection of the true model onto the specified model.³⁰ In contrast, with incorrect sampling weights, it is unclear what any other procedure (including inverse probability weighting) would estimate.

Finally, in discussing the DAGs and deriving the likelihood approach, we have assumed no within-group clustering of responses. This assumption is unlikely to hold for many complex surveys, including the one discussed here. In these settings, even if point estimates are correctly estimated, the corresponding standard errors may be too small, confidence intervals too narrow, and tests of significance overstated.^24,31,32 We ignored intracluster correlation for the purposes of simplicity, as our primary objective was understanding selection bias in association studies using complex surveys. However, for both the weighted unconditional regression and unweighted conditional regression approaches, robust standard errors may be obtained using a generalized estimating equations framework. The likelihood approach can also be extended to incorporate clustering through a mixed-effects model with cluster-specific random intercepts.

APPENDIX

Likelihood estimation as weighted logistic regression

Interestingly, as formally shown below, our likelihood approach can be rewritten as a weighted logistic regression without an offset, but with weights equal to $\left[\frac{P[N=0\mid M,N,L,S=1]}{P[N=0\mid M,N,L]}\right]$ for subjects with N=1 (i.e. cases) and $\left[\frac{P[N=0\mid M,N,L,S=1]}{P[N=0\mid M,N,L]}\right]\times \left[\frac{P[S=1\mid M,N=1,L]}{P[S=1\mid M,N=0,L]}\right]$ for subjects with N=0 (i.e. non-cases).

Note that the ratio $\left[\frac{P[N=0\mid M,N,L,S=1]}{P[N=0\mid M,N,L]}\right]$ is present in the weights of both cases and non-cases and therefore is not essential for reducing bias. In contrast, the ratio $\left[\frac{P[S=1\mid M,N=1,L]}{P[S=1\mid M,N=0,L]}\right]$ is present only in the weight for non-cases, making it essential for accounting for selection bias. This latter term eliminates selection bias due to differential selection probabilities because it standardizes the selection probability experienced by non-cases to match that of cases. In principle, these weights will be less variable than the standard inverse probability weights. To see why, consider a situation in which the outcome does not predict selection, and therefore weights are unnecessary to adjust for selection bias. In this scenario, the likelihood weights appropriately reduce to 1.0, whereas the standard inverse probability weights reduce to 1/P[S = 1|M,L], thus generally leading to loss of efficiency.

Proof of likelihood estimation of directed acyclic graph presented in Figure 6 as weighted logistic regression

We start by noting that individual contributions to the score equation for the likelihood approach are of the form $U=h(M,L)\left[N-\mathit{expit}\left(\mathit{log}\left[\frac{P[S=1\mid M,N=1]}{P[S=1\mid M,N=0]}\right]+\alpha +{\beta }_{1}M+{\beta }_{2}L\right)\right]$ where h(M,L) = (1,M,L′).

Let $B=\mathit{expit}\left(\mathit{log}\left[\frac{P[S=1\mid M,N=1]}{P[S=1\mid M,N=0]}\right]+\alpha +{\beta }_{1}M+{\beta }_{2}L\right)$ and B^* = expit(α + β₁M + β₂L).

Then, one observes that

$$\begin{array}{l}N-B=\frac{(N-B)}{B(1-B)}B(1-B)\\ =\frac{{(-1)}^{(1-N)}}{B^N{(1-B)}^{(1-N)}}B(1-B)\\ =\frac{{(-1)}^{(1-N)}}{{\left(\frac{\tau (M,N=1)}{\tau \left(M,N=0\right)}\right)}^N{B}^N{(1-B^{\ast })}^{(1-N)}}B(1-B^{\ast })\\ =\frac{(N-B^{\ast })}{{\left(\frac{\tau (M,N=1)}{\tau (M,N=0)}\right)}^N{B}^{\ast }(1-B^{\ast })}B(1-B^{\ast })\\ =\frac{(N-B^{\ast })}{{\left(\frac{\tau (M,N=1)}{\tau (M,N=0)}\right)}^N}\frac{B}{B^{\ast }}\\ =\frac{(N-B^{\ast })}{{\left(\frac{\tau (M,N=1)}{\tau (M,N=0)}\right)}^{(N-1)}}\frac{(1-B)}{(1-B^{\ast })}\\ ={\left(\frac{\tau (M,N=1)}{\tau (M,N=0)}\right)}^{(1-N)}\frac{(1-B)}{(1-B^{\ast })}(N-B^{\ast })\end{array}$$

proving the result.