Collective cell traction force analysis on aligned smooth muscle cell sheet between three-dimensional microwalls

Abstract

During the past two decades, novel biomaterial scaffold for cell attachment and culture has been developed for applications in tissue engineering, biosensing and regeneration medicine. Tissue engineering of blood vessels remains a challenge owing to the complex three-layer histology involved. In order to engineer functional blood vessels, it is essential to recapitulate the characteristics of vascular smooth muscle cells (SMCs) inside the tunica media, which is known to be critical for vasoconstriction and vasodilation of the circulatory system. Until now, there has been a lack of understanding on the mechanotransduction of the SMC layer during the transformation from viable synthetic to quiescent contractile phenotypes. In this study, microfabricated arrays of discontinuous microwalls coated with fluorescence microbeads were developed to probe the mechanotransduction of the SMC layer. First, the system was exploited for stimulating the formation of a highly aligned orientation of SMCs in native tunica medium. Second, atomic force microscopy in combination with regression analysis was applied to measure the elastic modulus of a polyacrylamide gel layer coated on the discontinuous microwall arrays. Third, the conventional traction force assay for single cell measurement was extended for applications in three-dimensional cell aggregates. Then, the biophysical effects of discontinuous microwalls on the mechanotransduction of the SMC layer undergoing cell alignment were probed. Generally, the cooperative multiple cell–cell and cell–microwall interactions were accessed quantitatively by the newly developed assay with the aid of finite-element modelling. The results show that the traction forces of highly aligned cells lying in the middle region between two opposing microwalls were significantly lower than those lying adjacent to the microwalls. Moreover, the spatial distributions of Von Mises stress during the cell alignment process were dependent on the collective cell layer orientation. Immunostaining of the SMC sheet further demonstrated that the collective mechanotransduction induced by three-dimensional topographic cues was correlated with the reduction of actin and vinculin expression. In addition, the online two-dimensional LC–MS/MS analysis verified the modulation of focal adhesion formation under the influence of microwalls through the regulation in the expression of three key cytoskeletal proteins.

1. Introduction

In tissue engineering, the mechanical properties of the external microenvironment surrounding cells play an important role in cell physiology, including migration, morphogenesis, proliferation, differentiation and apoptosis [1–7]. For example, the formation of focal adhesion and stress fibres in adherent cells is dependent on the stiffness of the extracellular matrix (ECM) [8–11]. In addition, the optimal ECM stiffness for mediating strong cell adhesion is affected by the concentration of immobilized adhesive ligands on the ECM surface [12]. Generally, the elasticity of substrate dictates the responses of cells, including fibroblasts, smooth muscle cells (SMCs), etc., through the cytoskeleton organization [13]. Mechanical stresses generated from the external microenvironment or cell cytoskeleton (e.g. cell traction force, CTF) in cell signalling play important roles in regulating many biological functions [9,14]. To date, the effect of the CTF on cell migration, proliferation and metastatic potential has been demonstrated in two-dimensional model systems [2]. Moreover, recent studies have demonstrated significant coupling between external and cell-generated forces at the single cell level [15,16]. In our recent study, CTFs which are generated by actomyosin interactions and actin polymerization have been shown to transmit to the ECM via focal adhesions on two-dimensional hydrogels [17,18]. Such CTF investigations in two-dimensional systems have so far paved the way for carrying out quantitative analysis of cell morphogenesis in vitro.

Several in vivo studies have demonstrated that a single cell migrates by exerting the CTF on its surrounding ECM through the cell's leading and trailing edges. On the other hand, the mechanotransduction of a group of cells, e.g. cell sheet, which is actually involved in major biological processes such as morphogenesis, wound healing and tissue repair is not thoroughly understood [19–21]. A recent study has shown that the distribution and magnitude of the CTF concentrates on the periphery of the cell colony on planar substrates [22,23]. Another study of an advancing epithelial cell sheet has demonstrated that the CTF in at its leading edge during migration is predominately driven by cells at the rear end instead of those at the leading edge [24]. Collective mechanotransduction of a cell sheet has been known to trigger global phenotypic transformation. In cultured epithelial cells, non-confluent cells can switch from individual cells to fully differentiated, densely packed monolayers as a result of cell–cell contact [25,26]. The phenomenon of contact inhibition as mentioned above has been observed in other types of cells as well [27,28]. By tracking individual cell contour within Madin–Darby canine kidney cell sheet, cell–cell contact may not be the only condition required for growth inhibition [29]. However, such study has not provided any information on the dynamic behaviour of the CTF during contact inhibition of the cell sheet. Mechanical compression between opposing cells may provide an inhibitory signal against cell division [30]. In addition, cell–cell contact actually conducts stresses between adjacent cells, which eventually guides the orientation of cells along the minimal intercellular shear stress [31]. Cadherins, major transmembrane proteins at the cell–cell adherent junctions, act as the intercellular bridge between the cytoskeleton of two adjacent cells [19,32]. For instance, E-cadherin, which is essential for collective directional migration [33], is connected to integrin-based focal adhesions [34] and conducts the loading forces exerted by the actomyosin cytoskeleton at the cell–cell adherent junctions in an epithelial cell sheet [35]. Interestingly, collective cells grown under two-dimensional geometrical constraints can form different modes of collective migration under cell–cell interactions [36]. Elucidation of the mechanisms of three-dimensional collective mechanotransduction remains a tremendous challenge, because the mechanical stresses of a cell sheet are difficult to quantify with existing physical models.

Recent advances in the development of two-dimensional model systems for studying cell–substrate mechanics of single cells have been reported by several groups [23,24,37–39]. Among various biomaterials, polyacrylamide-based hydrogel (PAG), which can be engineered with variable chemical and mechanical properties, has proved to be an ideal experimental system for such study [40]. It has been first shown that the stiffness of PAG regulates cell motility through the alteration of contractile forces exerted by cells to the surrounding gel medium [13,41]. At the same time, the geometrical cue imposed on adherent cells from the external microenvironment has a significant impact on cellular functions [21]. Thus, micropatterning of cells on the flat two-dimensional PAG surface has been exploited over the past two decades for controlling the geometry and position of mammalian cells. For instance, two-dimensional micropatterned substrate has been used to investigate the cell shape index (CSI) and proliferation rate of single SMCs [42]. More recently, the three-dimensional architecture of microchannels has been used to control SMC morphology and phenotypes [43]. SMC-generated CTF is regulated by the Rho-kinase/ROCK, which affects mitogen-induced DNA synthesis [44] and the assembly of focal adhesions [45]. It is believed that mechanical homeostasis as well as chemical cues are essential in the mechanotransduction of tissues [5]. In order to elucidate the mechanochemical transduction of the actual cardiovascular system, the measurement of the CTF of a SMC sheet or layer will be necessary. The experimental and numerical data, particularly in terms of fabricating artificial arteries or aortas, are keys to the control of in vivo cell growth and tissue morphogenesis. Even in the surgical phase, the understanding of the CTF of a SMC sheet would add another level of understanding to the design of safe blood vessel equivalents [46].

Various experimental methods, including cell-populated collagen gel [47], thin silicone membrane [48] and force sensor array [49], have been developed to probe selected parameters involved in mechanotransduction of both individual cells and the cell layer during the past few decades. More recently, the arguably most acceptable method for quantifying mechanotransduction at the cell–substrate interface is CTF microscopy (CTFM) developed by Dembo & Wang [37]. There are another two types of CTFM which have been modified from the original versions as reported by Butler et al. [17] and Yang et al. [50]. All CTFM methods as mentioned above rely on the correlation computation of traction force with the use of Fourier transform. As a result, all conventional CTFM methods suffer from the same limitation in achieving high accuracy in the calculation of microbead displacement before/after cell detachment. Generally, the three-dimensional microenvironment is the predominant in vivo culture system for most vascular cells and tissues. For instance, both cells and cellular organelles sense three-dimensional mechanical forces such as shear stress of the hydrodynamic blood flow, mechanical loading from surrounding ECM and contractile forces exerted by adjacent cells [51]. Among various cells and tissues, the SMC functions and fate are highly subjected to the mechanotransduction between cells and surrounding three-dimensional microenvironment. Mechanical stresses produced from the surrounding physiological microenvironment, such as the ECM, neighbouring cells and so on, can influence the collective SMC proliferation and morphogenesis, which eventually contribute to the vasoactivity of the blood vessel. Until now, a mechanistic understanding on the mechanotransduction of the SMC layer in three-dimensional experimental systems which mimics the tunica media of blood vessels still remains to be elucidated. This shortage ushers the cooperation of numerical simulation to analyse the mechanical deformation and stresses on substrate induced by cultured cells.

CTFM is the most reliable approach for studying the cell layer-ECM mechanotransduction if a three-dimensional model system incorporated with the PAG-microbead layer was developed. In this study, we developed a new traction force microscopy assay modified from the conventional CFTM to probe the collective CTF of the SMC layer between two adjacent microwalls [40]. We first capitalized on our soft lithography approach in fabricating three-dimensional microstructures with microwall features in polydimethylsiloxane (PDMS) as the precursor of the three-dimensional microenvironment for probing mechanotransduction of a collective cell sheet [52]. Afterwards, a thin layer of PAG which contained well dispersed florescent microbeads was coated on the PDMS microwalls. To measure the elastic modulus of the PAG layer, atomic force microscopy (AFM) in combination with regression analysis was applied. Then, the dynamic process of cell alignment was probed by real-time cell imaging and quantitative analysis during the formation of a functional SMC sheet. The cooperative mechanical forces of the SMC layer were accessed by our recently developed finite-element analysis [53]. We demonstrated that the mechanotransduction of collective cells is affected by the topographic cues provided by the microwalls. At the same time, both cell–cell contact and cell–microwall contact influenced cell proliferation, cytoskeleton remodelling, focal adhesion, cell alignment and protein expression. Overall, we systemically elucidated the influences of contact guidance provided by the microwalls and cell–cell adherent interaction on the CTF distribution and mechanical stresses during the process of cell sheet assembly.

2. Material and methods

2.1. Cell culture

Human aortic smooth muscle cells (AoSMCs obtained from Lonza, Switzerland) were used herein. Cells were cultured in growth medium (SmGM basal medium supplemented with SmGM-2 SingleQuot Kit Suppl. and growth factors obtained from Lonza). Cells were kept in a CO₂ incubator at 37°C under 5% CO₂ atmosphere. The culture medium was changed every 2 days. Before cell passage and seeding, cells were washed with HEPES-buffered saline solution (ReagentPack subculture reagents obtained from Lonza) and detached from the flask by adding trypsin/EDTA solution (ReagentPack subculture reagents obtained from Lonza). The cell suspension was then transferred to a 15 ml Falcon tube and was centrifuged at 1000 rpm for 5 min. After removal of supernatant, the remaining cells at the tube bottom were resuspended by adding culture medium and transferred back to the cell culture flasks.

2.2. Fabrication of microstructured PDMS stamps

A master silicon mould was first prepared by a deep reactive ion etching system (Surface systems + Technology GmbH and Co.). Photoresist AZ5214 was coated on the silicon wafer mould by a spin coater (Delta 80BM) at a rotation speed of 4000 rpm for 30 s. Then, prebaking of the photoresist-coated silicon mould was carried out at 110°C on a hotplate for 105 s. After exposure and developing, the pattern was transferred from the silicon mask to the photoresist layer. The three-dimensional pattern of microwalls was etched into the silicon wafer by deep reactive-ion etching. After dry etching, the silicon wafer surface was passivated with a Teflon-like polymer for cleaning and demoulding. We fabricated the microwalls with height of 30 µm, width of 60–70 µm and length of 160 µm. The distance between the two opposing walls was 300 µm. In addition, the two adjacent microwalls along the same long axis were separated by a distance of 40 µm, which was found to increase the degree of confluence of primary SMCs by providing more free space among cells.

The silicone base and curing agent (Sylgard 184 kit) were mixed at a weight ratio of 10 : 1 and then cast over the silicon wafer with the inscribed microwalls. Then, the silicon mould with silicone curing reagents was put under vacuum for 10 min, repeated three times, and then stored at 80°C overnight. The following day, the sample was heated at 120°C for 2 h. When the silicon mould was cooled down to room temperature, the polymerized PDMS was peeled off and cleaned in a hexane bath overnight. Lastly, PDMS was washed in ethanol overnight and dried in an oven. The depth of the PDMS microstructure was validated by using a surface profiler (Alpha-Step IQ, KLA-Tencor Corporation). The micropatterned PDMS was cut into several circles of 15 mm diameter and put onto the 35 mm diameter Petri dishes with glass bottom. The sample was treated with Argon plasma to generate radicals on the PDMS surface before coating with a layer of PAG [54].

2.3. Preparation and functionalization of polyacrylamide gels

Acrylamide (40% w/v, Sigma) and N-N′-methylene-bis-acrylamide (BIS, 2% w/v, Sigma) were mixed at a ratio of 10% to 1% v/v in a solution of distilled water and ethanol. Solutions were degassed for 30 min using argon gas to optimize polymerization. Then, 0.2 μm fluorescent latex beads (Invitrogen Inc.) were ultrasonicated at 1/1000 volume concentration and were added to the solution. To obtain a thin layer of PAG, the solutions were cast over the PDMS surface and put under UV radiation at a distance of 15 cm for 15 min. To check the density of the beads, fluorescence microscopy was used to observe bead distribution.

As PAG is highly hydrophilic and chemically inert, a heterobifunctional cross-linker known as sulfosuccinimidyl-6(4′-azido-2′nitrophenylamino) hexanoate (sulfo-SANPAH, Sigma Pte Ltd.) was attached to the PAG surface before binding of adhesive ligand. Approximately 250 µl of the sulfo-SANPAH solution (dissolved into 1 mg ml⁻¹) was added per sample, which was then exposed to 365 nm UV light for at least 15 min until the solution turned from orange to dark red colour. The phenylazide group of sulfo-SANPAH was photoactivated and covalently linked to the PAG functional groups within the gel, whereas the succinimidyl ester group at the other end then reacted to the primary amines of cell adhesion proteins such as collagen. The gels were rinsed with PBS and stored in the dark. Afterwards, 0.2 mg ml⁻¹ collagen type I (BD Bioscience Inc.) which was diluted 10 times in PBS from 2 mg ml⁻¹ stock solution was added to the PAG surface and kept in the shaker at room temperature for 4 h in the dark. After collagen binding, the samples were rinsed with PBS three times under sterile conditions. Culture medium (1.5 ml) without FBS was added to the sample dishes, which were put into incubator at 37°C for at least 30 min. Before cell seeding, final sterilization of the PAG-coated PDMS microwalls with UV illumination for 15 min was required. Figure 1 shows the schematic illustration of the fabrication process of a PDMS micropatterned scaffold and, then coating with a thin layer of fluorescent microbead-embedded PAG.

Figure 1.

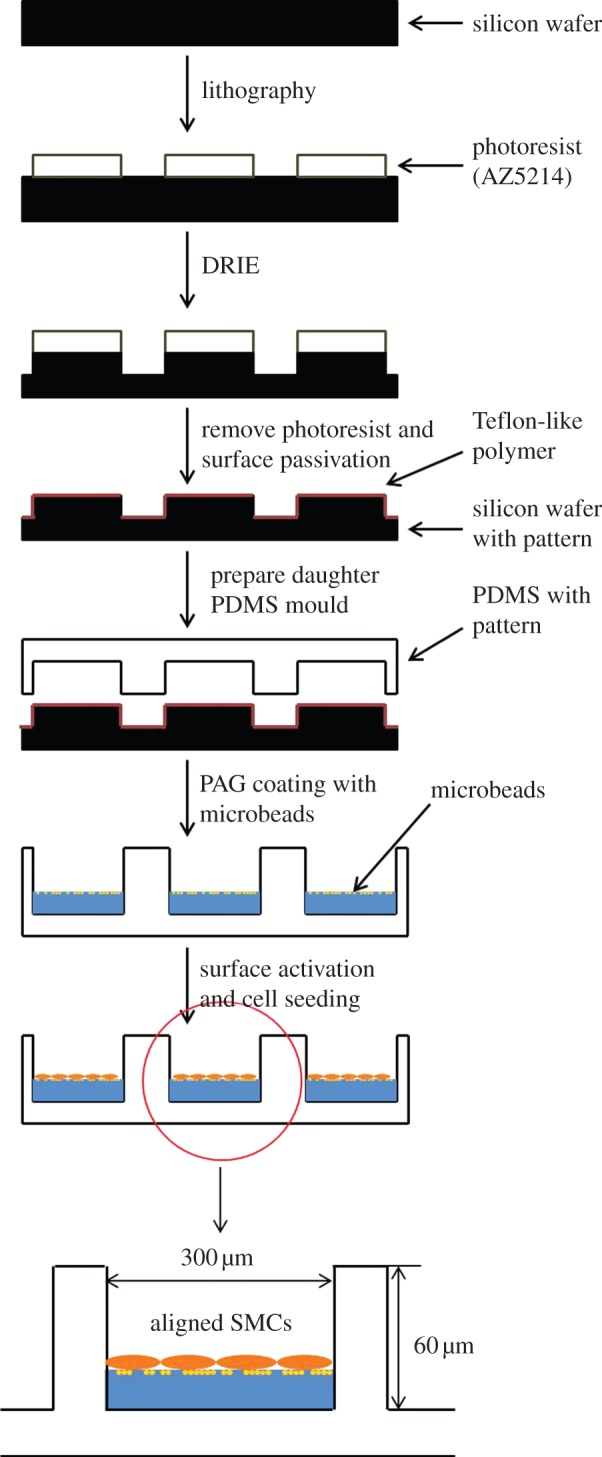
Schematic showing the fabrication process of PDMS micropatterned scaffold coated with a thin layer of fluorescent microbeads-embedded PAG. (Online version in colour.)

2.4. Cell seeding and image collection

The seeding density of AoSMCs on PAG-coated PDMS microwalls was around 10⁴ cells cm⁻² as confirmed by cell counting with a haemacytometer. Cell culture medium was refreshed every day. At certain times, transmitted light images of the AoSMCs seeded on the microwalls were taken using a 40× objective on a motorized microscope stage (BioPoint 2, Ludl Electronic Products) of an Olympus IX71 inverted microscope. During the experiment, the samples containing AoSMCs were kept at 37°C with temperature control 37-2 Digital and Heating Unit (Leica Inc.). The humidity of the stage and 5% carbon dioxide were maintained by the humidifier system (CTI-Controller 3700, Leica). In order to perform the CTF calculation of collective cells in the cell layer, both transmitted light and fluorescence images of the cell layer were taken as the ‘force load’ images. The phase contrast image determines the location and locomotion of collective cells at certain times (1 h, 4 or 7 days) after cell culture in three-dimensional microwalls. At the same time, the fluorescence (light source at 490 nm and emission at 515 nm) determines the positions of fluorescent microbeads. After trypsinization, cells were detached from the substrate and ‘null force’ images were taken again in the same image frame with both phase contrast and fluorescence microscopy. From the pair of fluorescent images (before and after trypsinization), the displacement of the fluorescent microbeads was determined and used for CTF computation.

2.5. Substrate displacement and cell traction force determination

A particle image velocimetry (PIV) program coded in Matlab was used to determine the displacement of fluorescent microbeads in the PAG layer on top of the PDMS microwall substrate. PIV is a visualization tool for calculating the bead displacement map by maximizing the intensity cross-correlation function between two pixel points on a pair of fluorescence images before and after trypsinization. The cross-correlation function is defined as

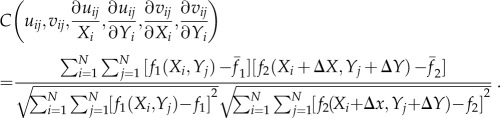2.1

The subscripts denote the pixel point (i,j). The relations between the pixels (X_i,Y_j) and 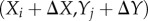 in two images are

2.2

2.3

where u_ij, v_ij are x and y displacements of the (i,j) pixel point; N is the total pixel number inside the interrogation window; f₁(X_i,Y_j) and f₂(X_i,Y_j) are intensities of the image at pixel point (i,j) in each image; 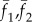represent the average values of f₁(X_i,Y_j) and f₂(X_i,Y_j) in each window; ΔX,ΔY are the shift (or overlap) of the interrogation window between two images.

Note that the value of C is between 0 and 1, the higher the value of , the more closely related the images at (X_i,Y_j) and (X_i + ΔX, Y_j + ΔY). Therefore, the objective is to numerically search for a location in the second image that is most consistent with the one in the first image, i.e. finding the location with maximum C. Because the search for maximum C involves all six variables 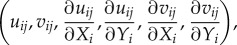 the computation has to be carried numerically. A free program MatPIV distributed under the GNU general public licence was adopted for our study [55–58]. The window size used for calculation is 8 × 8 pixels and 64 × 64 pixels for different trials. The location of the maximum value in C is then recognized as the mean particle displacements in the window.

2.6. Estimation of mechanical properties of collective cell traction force

The results obtained from the quantitative PIV process on the displacements of microbeads are input as boundary conditions for the subsequent finite-element analysis. The finite-element method (FEM) was implemented by ansys11 to determine the formation and stress of PAG substrate.

2.7. Characterization of elastic mechanical properties of substrate

AFM (Asylum research, model MFP-3D) was used to measure the mechanical properties of the PAG layer under physiological conditions [59,60]. The contact mode was chosen for the indentation of the PAG layer. The AFM probe is a silicon nitride cantilever (Sharpened Microlevers, Crest Technologies) with spring constant of 8.6 mN m⁻¹. Calibration was carefully carried out for the unloaded cantilever probe before each the test in order to reduce the thermal deviation. By controlling the velocity and indentation depth, the displacement of the AFM cantilever tip during the course of indentation in the z-direction and its deflection of the cantilever were recorded as the x- and y-axis of the force curve, respectively.

To estimate the elasticity of the PAG substrate, Hooke's law and Hertz's model were applied to data analysis [61]. The indentation and deflection are assumed in the z-direction (figure 2) and for the elastic modulus, the applied loading force F and elastic deflection of the cantilever d is

2.4

Figure 2.

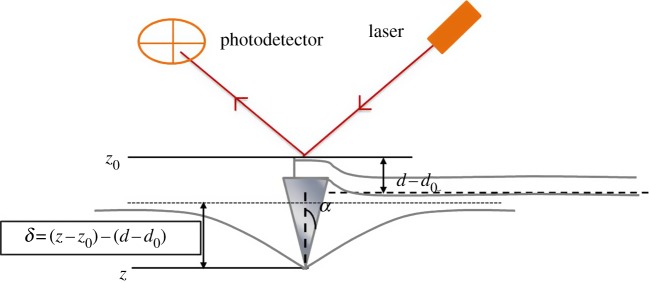
Schematic of the AFM indentation. The parameters shown in the picture are depicted in the graph [53,61]. (Online version in colour.)

On the other hand, the relation between the applied loading force F and small deflection δ on the elastic substrate can be modelled by the Hertzian model as follows

2.5

where E is the elastic modulus, υ is Poisson's ratio for a polymer and α is the half-cone angle of the tip shown in the figure 2.

By combining equations (2.4) and (2.5), we obtain the following indentation–deflection relation for the elastic modulus calculation.

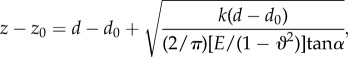2.6

where z₀ is the arbitrary tip position as long as it is above the zero contact point which locates at the infinite end where the surfaceis not deformed. d₀ represents the position of the non-deflected beam position. The experiment provides measures on z − z₀ and d − d₀ to allow us to calculate the Young modulus E of the indented surface.

2.8. Analysis of smooth muscle cell morphology and orientation

To track changes in collective cell morphology, phase contrast images were taken and an 850 × 1000 pixel field was chosen to quantify the cell morphology against culture time. The boundaries of SMCs were first outlined by MetaMorph. At least 50 cells from three frames were randomly chosen and analysed. Cells grown on flat PAG-coated PDMS substrates without microwalls were also studied as control groups. The deformation of cells can be quantified as

2.7

where S is the spreading area (projection area) and L is the perimeter of the cells. If the value of the CSI approaches 0, cells are highly elongated, whereas cells are more spread when the CSI equals 1.

The degree of orientation of a single cell was defined by calculating the percentage of alignment

2.8

where A is the cell width in the y-axis and B is the cell length in the x-axis. For the micropatterned substrate, the x-axis defines as the microwalls’ longitudinal axis.

2.9. Immunofluorescent staining

SMCs grown between microwalls or on flat films were washed twice with prewarmed PBS, fixed in 3.7% paraformaldehyde for 10 min, permeabilized by 0.05% Triton X-100 for 5 min and then blocked in 1% BSA/PBS solution at room temperature. For vinculin staining, monoclonal anti-vinculin FITC antibody (Sigma) was applied at 1 : 50 dilution at 4°C overnight. For cytoskeleton staining, samples were incubated in Alexa Fluor 546 phalloidin (Invitrogen) with 1 : 40 dilution in 1% BSA/PBS solution at room temperature for 1 h. After washing twice with PBS, DAPI (Invitrogen) staining was performed for 10 min after all other staining. Images were taken with an Olympus IX71 fluorescence microscope.

2.10. Protein extraction, digestion, labelling with iTRAQ reagents and online two-dimensional LC–MS/MS analysis

The sample was prepared and analysed according to previously published work [62,63]. Cells were harvested and lysed in 100 µl of 8 M urea, 4% (w/v) CHAPS and 0.05% SDS (w/v) on ice for 20 min with regular vortexing. Then, samples were centrifuged at 15 000 for 60 min at 4°C. The supernatant was removed, and protein was quantified by using the two-dimensional quant kit (GE Healthcare). After the addition (four times) of cold acetone at −20°C for 2 h for precipitation to the sample volume, each sample was dissolved in the buffer solution and denatured, and cysteines were blocked as described in the iTRAQ protocol (Applied Biosystems). Each sample was digested with 20 µl of 0.25 µg µl⁻¹ sequence grade modified trypsin (Promega) solution at 37°C overnight [62]. SMCs grown between microwalls were labelled with iTRAQ 117 and control SMCs grown on the flat substrate were tagged with iTRAQ 116. The labelled samples were then pooled in a fresh tube before analysis.

The analysis was performed on an Agilent 1200 nanoflow LC system (Agilent Technologies) interfaced with a Q-TOF 6530 mass spectrometer (Agilent Technologies). In the first step of separation, 4 µg of the combined peptide mixture was loaded onto the polysulfoethyl A strong cation exchange column (0.32 × 50 mm, 5 µm) and was eluted by injecting gradient ammonium formate solution with concentrations of 20, 40, 60, 80, 100, 300, 500 mM and 1 M. The eluted peptides were analysed by a chip (Agilent Technologies) that is integrated with large capacity enrichment column and C18 reverse phase column. In each elution, the retained peptides were eluted with gradient mixture of buffer A (ddH₂O/0.1% formic acid) and buffer B (acetonitrile with 0.1% formic acid) at a flow rate of 0.3 μl min⁻¹ [63]. MS/MS generated spectra were deconvoluted and analysed using Spectrum Mill (Agilent Technologist, CA, USA). The peptides were identified against the UniProtKB/Swiss-Prot protein database (Geneva, Switzerland) for Homo sapiens [63].

3. Results and discussions

3.1. PDMS microwalls for cell traction force measurement

The polymerizations of PDMS were conducted by mixing silicone base and curing agent (Sylgard 184 kit). The depth of microwalls used herein was confirmed as 60 µm [52]. In order to measure the CTF exerted on a deformable substrate, the PDMS microwall substrate was evenly coated with a thin layer of PAG with optimized stiffness. The thickness of PAG was around 10 µm. At the same time, the PAG layer was embedded with 0.2 µm fluorescent microbeads for tracking displacement of the gel microdomain in the CTFM assay. First, the phase contrast image demonstrated the successful formation of a rather clear PAG layer without any detectable particulate on the surface of PDMS microwalls (figure 3a). The excellent optical quality facilitates microscopy monitoring of cellular processes and immunofluorescence staining. Second, the distribution of fluorescent microbeads dispersed in the PAG layer was uniform as confirmed with fluorescence microscopy (figure 3b). Figure 3c showed the scanning electron microscopy (SEM) images of the discontinuous PDMS microwalls coated with a thin layer of PAG. Compared with the smooth surface of PDMS (figure 3d), the result indicated the uniform distribution of the PAG layer, which was composed of closely packed meshwork [64]. Moreover, the microstructure of the PAG coating is supported by the cross-linked topographic feature on the SEM image under high magnification (figure 3e).

Figure 3.

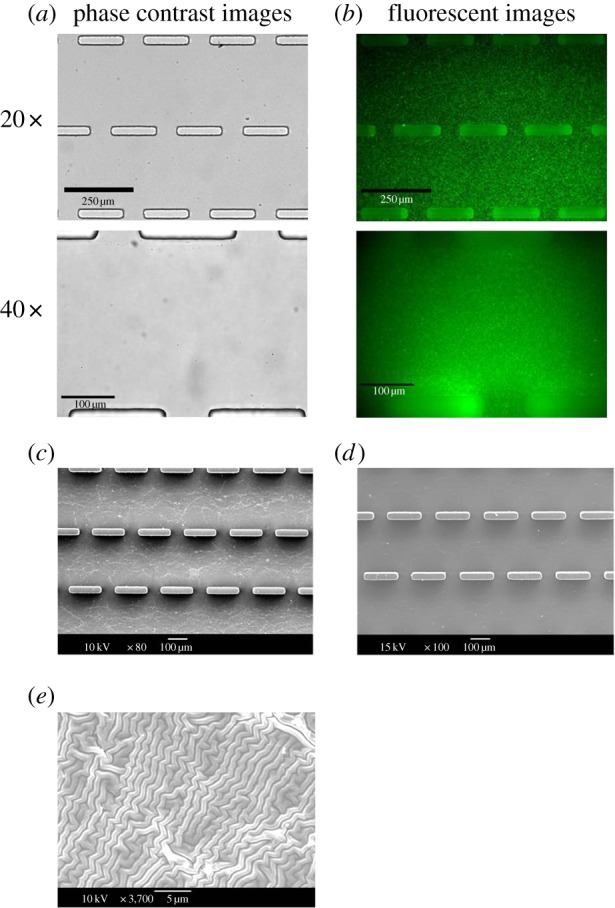
Micropatterned PDMS coated with a layer of PAG. (a,b) Phase contrast images and fluorescent images of PDMS microwall were taken under 20× and 40× magnifications. The microbeads were uniformly distributed in the PAG layer. (c,d) SEM images of the PDMS–PAG substrate and only PDMS microwalls show the PAG coated on the PDMS. (e) SEM image of the PAG microstructure under the optimal PAG concentration used in our CTFM study. (Online version in colour.)

3.2. Polyacrylamide-based hydrogel substrate stiffness measured by atomic force microscopy

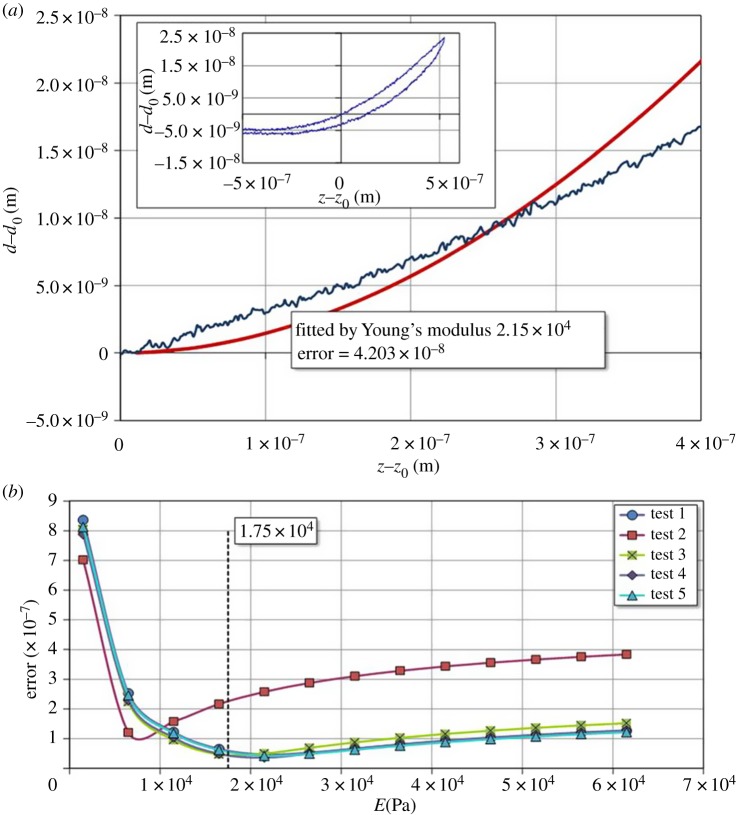
The stiffness data of PAG measured by AFM are shown in figure 4 (inset). The deflection of cantilever probe (d − d₀) versus indentation (z − z₀) was presented. This functional relation between the two parameters can also be calculated using the theoretical Hertzian model from equation (2.6) if Young's modulus is provided. With the given experimental data, the Young modulus can be estimated by minimizing the errors between experimental data and theoretical calculations [52]. One example is shown in figure 4a as an appropriate Young's modulus is chosen. The loading curve by AFM can be fitted with minimum errors between the experimental data and the calculated values. The five set AFM measurements were analysed using the regression method for determining the optimal values of Young's modulus for each set of data as shown in figure 4b. The results indicated that the average value of Young's modulus was 17.5 kPa with s.d. of 6.52 kPa. The result determined herein agreed well with other Young's modulus values of PAG which was probed by AFM indentation or other mechanical tests reported by other groups [12,65]. Moreover, numerical values of the fitted Young's modulus were required for the subsequent finite-element simulation of the CFT induced by SMCs on PAG–PDMS substrate.

Figure 4.

(a) One deflection–indentation curve for measuring Young's modulus of PDMS–PAG substrate using the AFM contact mode. (b) Errors between the calculated and experimental measures of AFM indentation curve for Young's modulus measurement of PDMS–PAG substrate by using the contact mode. The average value of Young's modulus is 17.5 kPa and the s.d. is 6.52 kPa. (Online version in colour.)

3.3. The morphology and phenotype control of smooth muscle cell

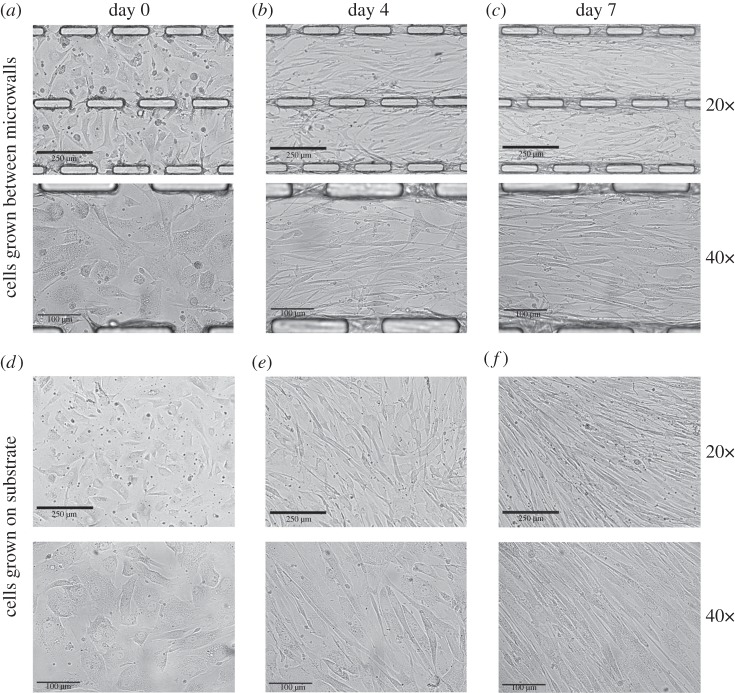
To observe the role of three-dimensional geometrical constraints on the collective mechanical behaviours of a multiple-cell sheet, human aortic SMCs were directly seeded on a PAG layer containing fluorescent microbeads in all regions between the microwalls. The cell morphology and alignment within the cell layer were monitored for 10 days under physiological conditions. During the course of imaging, the sample was secured on the microscopic stage at 37°C and supplied with 5% carbon dioxide in the incubator. Figure 5 showed a series of phase contrast images of the cell sheet cultured on the PAG-coated PDMS microwall substrate during the 10 day period. When the cell density on the microwall substrate was low immediately following cell seeding (day 0), SMCs were found to express fibroblast-like morphology and to adopt random orientation as shown in figure 5a. Moreover, there was no significant difference in the cell orientation and morphology between SMCs on microwall substrate and flat PDMS substrate (figure 5d). The result indicated that the constraints from a pair of adjacent microwalls did not significantly affect the cell shape and morphology when the cell–cell contacts were absent under low cell density at day 0. From day 0 to day 4, SMCs seeded on the PAG layer between the PDMS microwalls significantly elongated following the increase in cell density. At the same time, SMCs started to align along the direction of the long axis of the microwall (figure 5b). The result as mentioned above was supported by the constraint on SMC alignment which had been reported in SMCs grown between the PDMS microchannel [52]. During the intense period of cell proliferation, cells reached confluence after 7 days of culture. As shown in figure 5c, SMCs on microwall substrate were mostly found to be switched from fibroblast-like to elongated morphology and aligned well along the microwall's long axis after 7 days of culture. By contrast, various groups of SMCs grown on the flat PDMS substrate randomly aligned in different directions within a significantly smaller region with area of around 150 × 150 μm² with the absence of highly collective cell alignment across a larger area found in the SMCs on the microwall substrate, e.g. 300 × 600 μm² (figure 5f). In other words, flat PDMS did not provide any unidirectional guidance on the intended direction of a cell sheet when compared with microwalls. Of course, it does not mean that there is no alignment of cells in the absence of microwalls on the substrate. Instead, the alignment is due to contact from nearby cells. Figure 5 indicated that imprinted discontinuous microwalls successfully guided the direction of collective alignment of SMCs via the imposed boundary constraints.

Figure 5.

Phase contrast images of SMCs grown on PDMS microwalled substrate (a–c) and flat PDMS (d–f) substrate under 20× and 40× magnifications, both with PAG coating at various time after cell seeding including 1 h (a,d), 4 days (b,e) and 7 days (c,f).

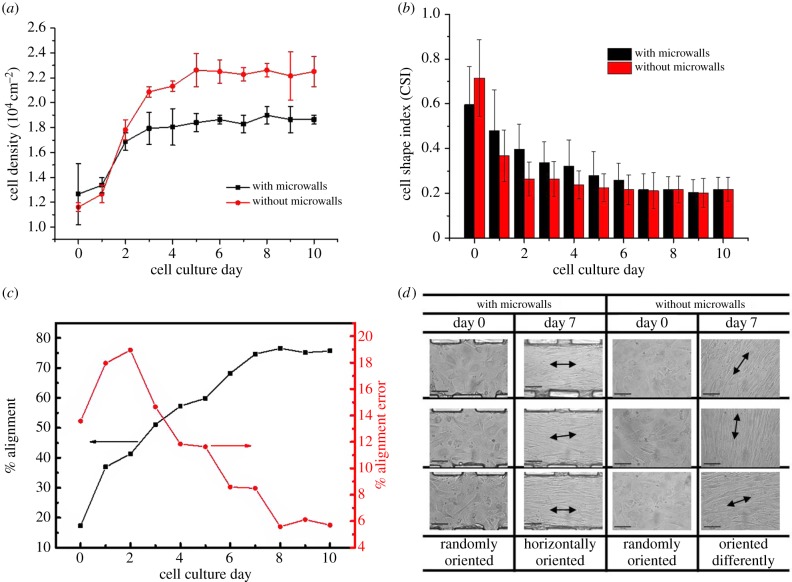
In addition to temporal tracking of the morphology switching of the SMC layer, quantitative analysis was needed to elucidate the effect of constraints from microwalls on cells. Figure 6a shows the SMC density on the PDMS microwall and flat PDMS substrates against time of culture. In general, the result indicated that intense cell growth only occurred during the first 4 days of cell culture. In addition, the initial growth rate of cells (slope of the cell density versus time plot from day 0 to day 4) for SMCs on microwalled substrate is 33% lower than that on flat substrate. The trend as mentioned above was likely caused by the combined three-dimensional geometrical and mechanical constraints induced by the parallel microwalls on the highly proliferative SMCs during early cell culture. After 5 days of culture, the SMC density ceased to increase further on both types of substrates as cells reached confluence. At the same time, the projected area of individual cells was reduced to a critical value when cell–cell contact inhibition totally dominated over further cell division. In addition, the steady-state cell density of SMCs grown on microwalled substrate after day 5 was 20% lower than that of flat PDMS. The result as mentioned above further exemplified the physical effect of parallel discontinuous microwalls in moderating the extent of cell proliferation. After 7 days of culture, the cells completely shifted from the fibroblast-like to elongated morphology as the CSI value was significantly reduced as shown in figure 6b. The reduction of CSI indicated that the cell body was significantly elongated after 3 days of culture compared with the non-polarized cell shape immediately after cell seeding on the two substrates. Moreover, the reduction of CSI from day 0 to day 2 for SMCs grown on microwalled substrate is quite significant, indicating cells found their preferred alignment if there are microwalls present. This change of CSI suggested that the microwalls accelerated the phenotype shift of SMCs. In addition, the percentage of cell alignment on microwalled substrate significantly increased from 16% to 76% after 7 days of culture, whereas the percentage error reached maximum level around 2 days and continued to decline as shown in figure 6c. The percentage of cell alignment is not applicable to SMCs grown on flat PDMS herein because of the lack of a reference axis. Figure 6d shows the phase contrast images of cells at various locations on day 0 and day 7 where the unidirection alignment of cells can be clearly observed under the presence of microwalls on day 7. The cells on flat PDMS substrate have different alignment at different locations, which is mostly affected by the neighbouring cells.

Figure 6.

Cell density, morphology and orientation of SMCs grown on microwalls and flat PDMS substrate. (a) Density of SMCs during 10 days’ culture. (b) CSI of SMCs during 10 days’ culture. Error bars represent mean values ±s.d. from at least 40 cells in three different frames. The cut frame is 850 × 1000 pixels (1 pixel = 0.334572 µm). (c) % Alignment and % alignment error of SMCs grown between microwalls. (d) Selected locations for cells at day 0 and day 7. (Online version in colour.)

To quantify the statistical differences for cells cultured on microwalled channels and flat PAG substrate, a t-test was performed for the differences in cell density and CSI. Table 1 shows the p-values of the two parameters for different days of culture and as expected from figure 6a,b. The result indicated that the cell density was significantly higher on flat substrates than that on microwalled channels starting from day 4 and onwards. The result indicated that microwalls are effective in guiding the directional alignment of a confluent cell sheet, whereas the flat substrate is more suitable for cell proliferation.

Table 1.

List of p-values from t-test for the cell density and CSI shown in figure 6. The italic data indicate significant differences between cells on patterned and flat PAG substrate.

day	CSI		density
	t0	p-value	t0	p-value
0	−0.8531	0.2281	0.7348	0.2695
1	0.8987	0.2175	1.3093	0.1408
2	1.7071	0.0932	−1.5119	0.1139
3	1.0434	0.1867	−3.8125	0.0312
4	1.0892	0.1779	−3.7417	0.0323
5	0.8047	0.2399	−4.8107	0.0086
6	0.7524	0.2532	−6.7361	0.0107
7	0.0839	0.4692	−7.8001	0.0022
8	0.0210	0.4923	−7.1119	0.0029
9	0.0518	0.4810	−2.7386	0.0357
10	−0.0463	0.4830	−5.2842	0.0170

3.4. Traction forces and stress distribution of aligned multiple-cell sheet

The deformation and stress analysis of the PAG layer is implemented by FE software ansys12. Starting with the geometry of a PAG gel with dimension of 334 × 284 × 10 µm, the whole domain (PAG substrate) is discretized by isoparametric, 20-node brick element SOLID186 (figure 7). The boundary conditions were specified displacements from PIV results, as shown in figure 8a(ii)–d(ii), at corresponding nodes on the surface underneath the cell. The nodes to the bottom of the substrate are fixed, because PAG is constrained to the microchannel. A flat PAG–PDMS substrate in figure 8d(i)) was used as a control group for comparisons. Material properties of PAG are listed in table 2 for reference.

Figure 7.

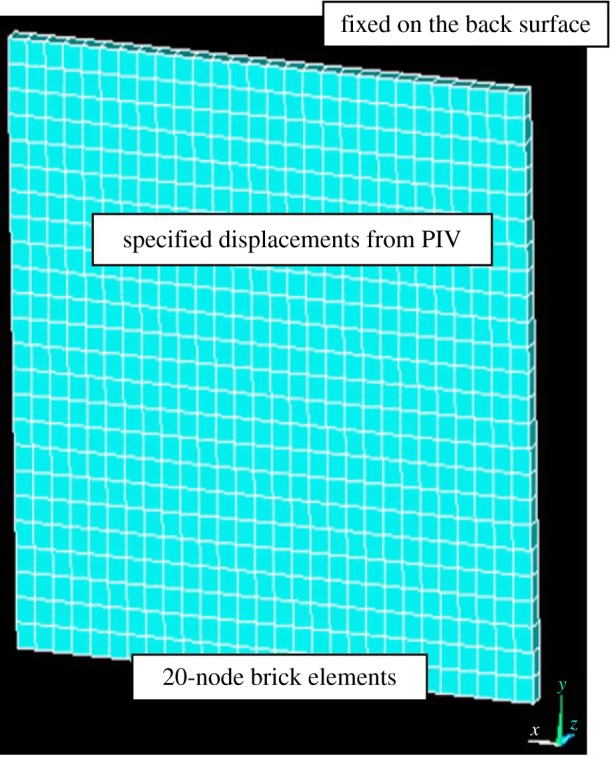
Coordinates and geometry of PAG of 334 × 284 × 10 for finite-element analysis. (Online version in colour.)

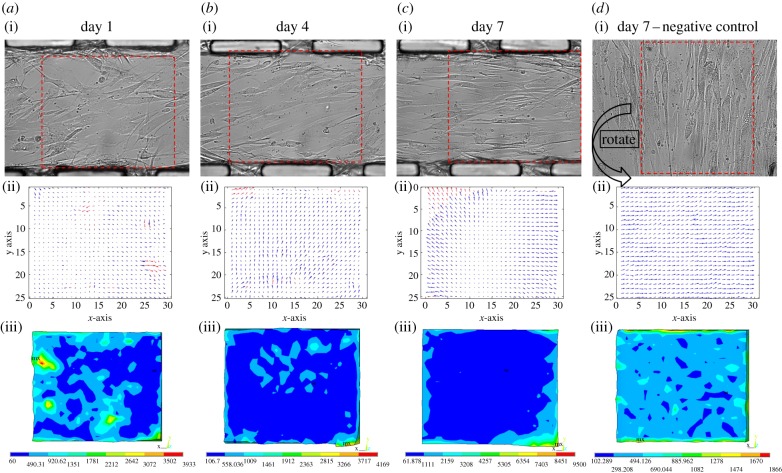
Figure 8.

The distribution of CTFs and Von Mises stresses of the collective SMCs against days of cell culture on PAG–PDMS microwall patterned substrate and flat PAG–PDMS substrate. (a–d(i)) The phase contrast images were taken under 40× magnification with resolution of 850 × 1000 pixels. (a–d(ii)) The displacements of microbeads processed from the pair of fluorescence images before/after trypsinization with the calculation of PIV. The window sizes were chosen to be 64 × 64 pixels. (a–d(iii)) Von Mises stress distributions of collective SMCs on PAG–PDMS simulated by FEM analysis.

Table 2.

Material property for finite-element analysis.

Young's modulus	Poisson's ratio	Mooney–Rivilin constant C10	Mooney–Rivilin constant C01	Mooney–Rivilin constant compressibility
1.75 × 104	0.495	1.75 × 104	1.75 × 104	0.00669

On day 1, after cell seeding (figure 8a(i)), SMCs attached well to the PAG–PDMS microwalled substrate, whereas some cells adopted fibroblast-like morphology and others were on the verge of transforming into elongated morphology. The results of CTF maps in the selected areas (outlined with red dotted line) indicated that the directions and magnitudes of CTFs located adjacent to the microwalls were non-polarized and random, respectively (figure 8a(ii)). The Von Mises stress was calculated as follows

3.1

At this early stage, the intercellular interactions were not strong enough, so that the orientations of individual cells as well as the high stress areas were quite random and discrete (figure 8a(iii)). Such a stress represents the energy equivalent magnitude of all stress components. High Von Mises stress indicates either a high tensile or compressive stress. Also noted that the microwalls imposed constraints on cells at single-cell level and therefore their effects were not significant.

As the cell culture proceeded to day 4, many cells had already spread out but not overlapped each other yet (figure 8b(i)). At this stage, most cells started to adopt a highly elongated morphology. Unlike the arbitrary orientations of cells on the day 1 (figure 8a(ii)), the CTF vectors caused by the incomplete cell sheet on day 4 (figure 8b(ii)) were mostly pointing towards the right-hand side of the microwalls. Moreover, a zone of low stress started to evolve at the entire bottom half and partial top half of the selected area of the SMC layer between the parallel microwalls (figure 8b(iii)). The results indicated that the intercellular interactions played an essential role in the formation of a multiple-cell sheet, whereas the microwalls confined the direction of cell alignment and triggered stress reductions across the SMC layer. A major component of intercellular adhesion is the cadherin complex that is tightly connected with the cytoskeleton inside cells. Meanwhile, the organization and transformation of the cytoskeleton can influence the CTF transmission to the ECM through integrin-based focal adhesions. In other words, intercellular interactions among multiple cells could affect the distribution of CTFs. In addition, the microwalls impose much more significant boundary conditions on the edges of an incomplete cell sheet.

As cell density increased, the intact cell layer became confluent around 7 days, which was proved by the slight overlapping between the cell membrane of adjacent cells (figure 8c(i)). There was no more free space for additional SMCs to adhere on the microwall substrate. The spatial map of CTFs within the controlled region during SMC alignment from day 4 to day 7 (figure 8b(ii),c(ii)) was found to be altered. The traction forces became more uniform as cells were well aligned along the microwalls and evolved as a cohesive structure in the selected area of the PAG layer (figure 8c(ii),c(ii)). As shown in figure 8c(ii), the magnitude of CTFs at the centre of the aligned cell sheet became significantly smaller than those at the periphery of the cell sheet, which is due to the boundary effects of the cell colony induced by the microwalls [22]. At the same time, the low stress zone had completely covered the entire selected area of the aligned cell sheet (figure 8c(iii)). For cells grown on the flat substrate, CTFs with similar magnitude across the entire controlled region were all pointing towards a random direction of cell elongation (figure 8d(ii)). The result basically indicated that cell–microwall interactions significantly changed both the magnitude and the direction of local CTFs in the controlled region. This was also clearly demonstrated by the fact that the directions of the CTFs near the microwalls were aligned along the wall, whereas the CTFs near the gap between microwalls were pointing more randomly. These observations were reinforced by the control group in figure 8d(ii),(iii), where the free grown cells on a flat substrate are less organized, the CTFs were distributed more randomly and the low stress zone was absent. Figure 8a(ii)–c(ii) reveals that as cells form a more complete sheet, so the imposed boundary constraints by microwalls became more substantial. The well-aligned cells on day 7 implied that individual cells relied less on cytoskeleton remodelling such as actin polymerization, because interactions among cells could uphold them as a cohesive unit without highly dense internal cytoskeletal structures and focal adhesion. This idea can be schematically illustrated as shown in figure 9, which provides a sound explanation of the computational results in figure 8c(ii). It must be noted that the geometry of the system used herein was rather different from the traditional assay with cells surrounded by an isotropic medium.

Figure 9.

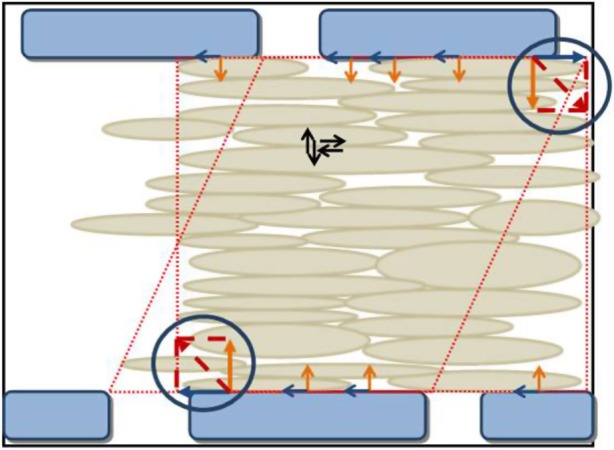
The schematic drawing of CTFs by the collective SMCs when cell sheet is completely formed. (Online version in colour.)

3.5. Immunofluorescent staining

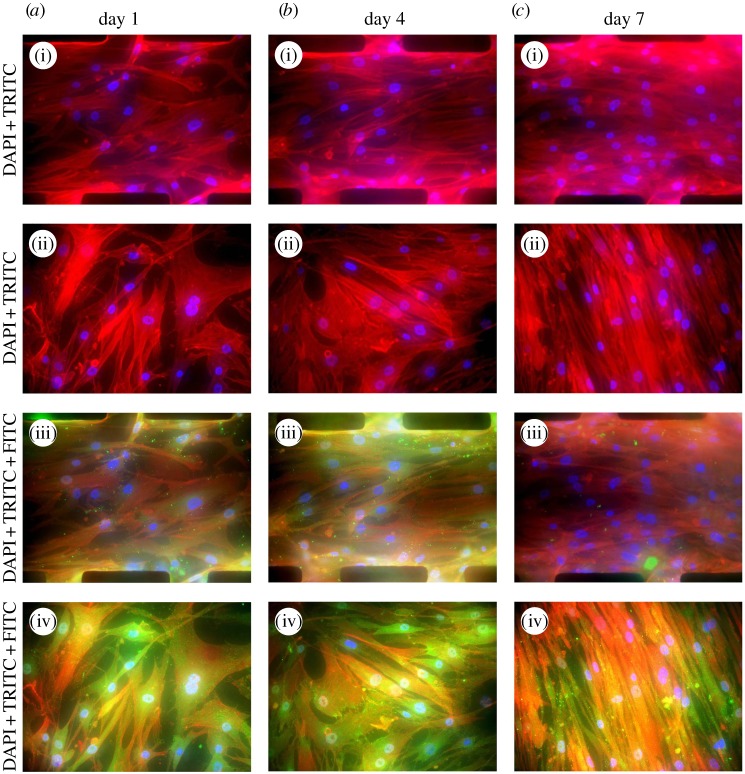
In order to verify our previous postulation on the change in cytoskeleton structure of SMCs owing to the formation of a collective cell sheet, immunostained SMCs grown on microwall and flat substrates were imaged with fluorescence microscopy. As shown in figure 10a–c(i) and a–c(ii), actin immunostaining (red) clearly indicated the presence of stressed fibres in cells. The intensity of stained actin in the case of flat PDMS on day 7 was much higher than that of microwall substrate, which supported our claim that significantly less actin was polymerized when the complete cell sheet was formed. The morphology of SMCs switching from fibroblast-like to elongated-like was also consistent with phase contrast images in figure 5. For SMCs cultured between microwalls (figure 10a–c(i)), the levels of actin expression were all lower than those grown on flat substrates (figure 10a–c(ii)).

Figure 10.

Spatial distributions of F-actin (red: TRITC), vinculin (green: FITC) and nucleus (blue: DAPI) for SMCs cultured on microwall patterned (a(i),a(iii), b(i),b(iii),c(i),c(iii)) and flat (a(ii),a(iv),b(ii),b(iv),c(ii),c(iv)) PDMS–PAG substrates on day 1, day 4 and day 7.

In addition to actins, vinculin is another cytoskeletal protein of interest because vinculin concentrates at focal adhesion plaques on the surfaces of mammalian cells. On day 1, focal adhesions composed of vinculin clusters (green spots on figure 10a(iii),(iv)) appeared for SMCs between microwalls and on flat substrate. Cells generally prefer to establish cell–wall interactions along the wall. This might be due to the additional physical cue provided by the wall to form focal adhesions. Interestingly, the density of vinculin clusters (evenly distributed throughout the cytoplasm) found in SMCs on the flat substrate was significantly higher than that on microwalled substrate. The presence of microwalls alone moderated the formation of focal adhesion in the absence of cell–cell interaction.

On day 4, the density of vinculin clusters found in SMCs on microwalled substrate slightly increased owing to the confluence-triggered contractile phenotype, particularly at locations close to the microwalls (figure 10b(iii)). By contrast, vinculin clusters significantly increased in numbers throughout the cytoplasm of non-aligned SMCs on flat substrate (figure 10b(iv)). The trend as mentioned above strongly indicated that the microwalls induced unidirectional constraints to both the cell–microwall and cell–cell interactions. From day 4 to day 7, the density of vinculin clusters for SMCs on microwalled substrate was significantly reduced, whereas the stressed fibres were well oriented along the microwalls (figure 10c(iii)). The density of vinculin clusters reached the highest level for those elongated cells on flat substrate after 7 days of culture (figure 10c(iv)). The fluorescence staining of vinculin during 7 days of culture implied that the microwalls were instrumental in downregulating the formation of focal adhesion, which yields lower CTF and a low stress zone for SMCs located in the centre between the two adjacent microwalls (figure 8).

More recently, Hall et al. [66] summarized several systematic approaches to CTFM analysis. They indicated two different computational methods for characterizing the cellular interactions with collagen matrix, i.e. the inverse and the forward computation methods. Both methods are useful in the study of cells completely embedded within the ECM. Cells cultured on a substrate are somewhat different from the three-dimensional embedded case, but the forward computational method is preferred owing to the widely available FEM commercial programs. The forward computational method is also found in other studies, for instance, Krauss et al. [67] and Koch et al. [68] present a computational approach based on the strain energy (deformation of matrix described by a mechanical strain energy function) in order to derive the stress field for the invasion of carcinoma cells into surrounding matrix. This approach is essentially the same as finite-element analysis except that they depend on the presumed energy functions from experiments. The value of T. M. Koch and Ben Fabry's work was that they captured the deformation and cast them in terms of strain energy, which is more illustrative, because energy is a scalar rather than a tensor.

3.6. iTRAQ analysis and differentially expressed proteins

In order to establish the biological difference between microwall-aligned SMCs and control SMCs, the protein expression profile for each type of cell was analysed by the two-dimensional nano-LC–MS/MS procedure. In our study, iTRAQ 117 represented cells grown on microwall substrate, whereas iTRAQ 116 represented control SMCs grown on a flat platform. Each MS/MS spectrum was searched against the human International Protein Index protein database and more than 200 proteins were detected. In our study, two or higher confidence unique peptides were identified and only protein quantification data with relative expression of greater than 1.2 or less than 0.8 were chosen for further analysis. According to these criteria, a total of 14 unique proteins, eight significantly upregulated and six significantly downregulated were identified, as shown in table 3.

Table 3.

List of differentially expressed proteins in SMCs grown between microwalls. No. peptides indicate the detected peptides (with 99% confidence) for the individual protein.

accession no.	protein name	no. peptides	iTRAQ 117/116	protein function
upregulation proteins
P52907	F-actin-capping protein subunit alpha-1	2	1.28	cytoskeletal organization
P23246	splicing factor, proline- and glutamine-rich	2	1.21	DNA and RNA binding protein
P48444	coatomer subunit delta	2	1.63	intercellular protein transport
P21796	voltage-dependent anion-selective channel protein 1	2	1.37	membrane protein, plays a role in ion transport and apoptotic process
Q13162	peroxiredoxin-4	3	1.35	regulates the activation of NF-kappa-B in the cytosol
Q96AG4	leucine-rich repeat-containing protein 59	2	1.46	required for nuclear import of FGF1
Q8NBS9	thioredoxin domain-containing protein 5	2	1.23	influences thioredoxin activity
P15144	aminopeptidase N	2	1.25	required in the final digestion of peptides
downregulation proteins
P67936	tropomyosin alpha-4 chain	6	0.13	binds to actin filaments, response to oxidative stress
P48643	T-complex protein 1 subunit epsilon	2	0.26	involved in the folding of actin and tubulin
Q09666	neuroblast differentiation-associated protein AHNAK	6	0.1	required for cell differentiation
O00299	chloride intracellular channel protein 1	4	0.26	ion transportation
Q02809	procollagen-lysine,2-oxoglutarate 5-dioxygenase 1	3	0.24	form hydroxylysine residues in –Xaa–Lys–Gly– sequences in collagens
P07195	l-lactate dehydrogenase B chain	2	0.21	involved in glycolysis

Based on the different molecular functions, 14 proteins could be subsequently classified into four catalogues. The group composed of three cytoskeletal proteins, five proteins involved in DNA synthesis/protein transportation, four signalling molecules and two metabolic enzymes. Among the group of three cytoskeletal proteins, F-actin-capping protein subunit alpha-1 (CapZA1), tropomyosin alpha-4 chain (TPM4) and T-complex protein 1 subunit epsilon (TCP-1) were all involved in actin polymerization and folding. For instance, F-actin-capping protein (CapZ) is an αβ heterodimer that is widely distributed in cells for limiting the growth of actin filaments. It also plays a significant role in the regulation of F-actin conformation, protein kinase C signalling, calcium sensitivity and focal adhesion reduction [69]. CapZA1, which is the α-subunit of CapZ, has been found to exhibit abnormal expression levels in breast cancer tissues [70]. At the same time, upregulation of CapZA1 would decrease the myofilament calcium sensitivity and inhibit polymerization at the fast growing end of actin filaments. In contrast to the upregulation of CapZA1, TPM4 and TCP-1 were significantly downregulated. Tropomyosin alpha-4 (TPM4) is one of the four isoforms of tropomyosins in human. A role of tropomyosin in muscle cells is to stabilize actin filaments and to alter focal adhesion structure [71]. T-complex protein 1 subunit epsilon (TCP-1) is essential in cytoskeletal functions by assisting in the folding of actin and tubulin. Therefore, the reduction in TPM4 and TCP-1 levels may affect the stability of a cytoskeleton-associated cluster such as focal adhesion under the effect of the physical cell–wall interactions. In other words, CapZA1, TPM4 and TCP-1 are all likely to play a key role in altering the motility and contractile function of vascular SMCs. Our findings were strongly supported by the fact that the focal adhesion composed of vinculin was significantly moderated under the influence of the microwalls.

4. Conclusion

We demonstrated the use of three-dimensional discontinuous microwalls for collective CTF measurements by coating thin layers of PAG-embedded microbeads onto the microwall substrate. Meanwhile, AFM was used to measure the elastic modulus of optimal PAG. To observe the influence of microwall constraints on the multiple-cell sheet, we tracked the process of morphology switches and cell alignment in culture for 7 days. The grown collective cell sheet can be potentially used as a patch for repairing damaged artificial arteries. As the cell sheet is grown between microwalls, the shape and thickness is well controlled and this uniform sheet is ready for further biological or clinical evaluation. With the newly developed collective CTFM assay, the results indicated significantly higher CTFs of aligned cells were found near the microwalls compared with those in the middle region between the microwalls. Interestingly, the spatial distributions of mechanical stress during the cell alignment process were correlated with the orientation of a collective cell layer. Moreover, we demonstrated the influence of physical constraint induced by microwalls on the formation of a low stress zone for the SMC layer. Immunostaining results showed significant reduction in expression of focal adhesion composed of vinculin for SMCs under the influence of microwalls. The results were further validated by the altered expressions of three major cytoskeleton-associated proteins by performing differential proteomic analysis between SMCs on microwall substrate and control SMCs.