Figure 9. Illustration of control input selection with model weight adaptation.

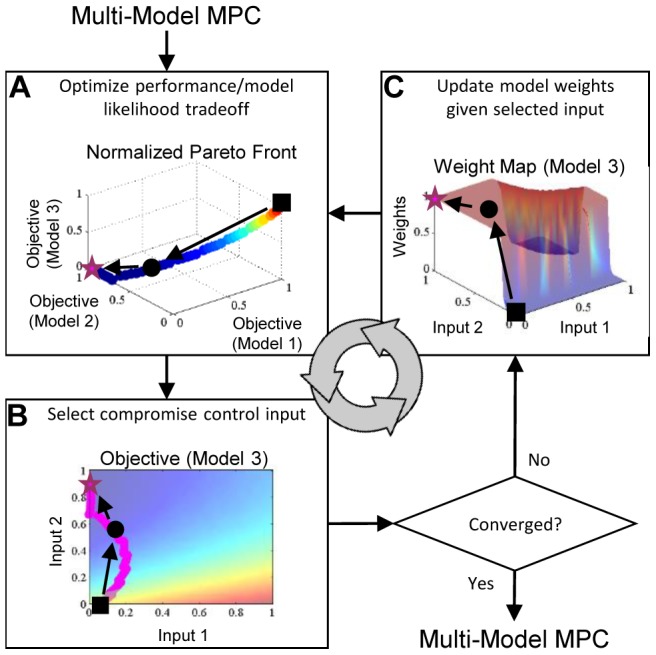
For a given prediction time interval in the control process, Pareto-optimal control inputs are computed by the multi-model MPC strategy by solving (7), which then enter an iterative process of control input selection and weight adaptation. (A) First, Pareto points are ranked with an initial weight vector ω₀ and the optimal point (example: black square) is selected using (8). (B) Next, the input vector corresponding to the selected optimal point (u ₁, black square) is identified. If the input vector continues to change above a pre-defined threshold, the process continues to the next iteration. (C) Given the current input vector (u ₁), a new weight vector (ω(u ₁), black square) is computed. The process continues and repeats (example: black circle, then magenta star) until the aforementioned stopping criterion is met. The final input vector (u_n, magenta star) is returned to the main control loop as the best compromise control strategy and used to update the prediction models in preparation for the next prediction time interval.