Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Jan 5;48(3):1736–1744. doi: 10.1021/es4040528

An LUR/BME Framework to Estimate PM2.5 Explained by on Road Mobile and Stationary Sources

Jeanette M Reyes 1, Marc L Serre 1,*
PMCID: PMC3983125  PMID: 24387222

Abstract

graphic file with name es-2013-040528_0003.jpg

Knowledge of particulate matter concentrations <2.5 μm in diameter (PM2.5) across the United States is limited due to sparse monitoring across space and time. Epidemiological studies need accurate exposure estimates in order to properly investigate potential morbidity and mortality. Previous works have used geostatistics and land use regression (LUR) separately to quantify exposure. This work combines both methods by incorporating a large area variability LUR model that accounts for on road mobile emissions and stationary source emissions along with data that take into account incompleteness of PM2.5 monitors into the modern geostatistical Bayesian Maximum Entropy (BME) framework to estimate PM2.5 across the United States from 1999 to 2009. A cross-validation was done to determine the improvement of the estimate due to the LUR incorporation into BME. These results were applied to known diseases to determine predicted mortality coming from total PM2.5 as well as PM2.5 explained by major contributing sources. This method showed a mean squared error reduction of over 21.89% oversimple kriging. PM2.5 explained by on road mobile emissions and stationary emissions contributed to nearly 568 090 and 306 316 deaths, respectively, across the United States from 1999 to 2007.

Introduction

Chronic exposure to ambient PM2.5 is linked to increased morbidity and mortality in many epidemiological studies1,2 and results in high population burden,3,4 making it a large public health concern. Hence quantifying accurate air pollution exposure has become paramount and has prompted different approaches to estimate chronic PM2.5 levels across space and time.

As our awareness of the impact of air pollution has increased, so has the interdisciplinary nature of exposure assessment. Researchers from these disciplines range from air pollution scientists to epidemiologists to risk assessors who are all involved in better understanding air pollution processes and its health effects. Disciplines also extend to cost-benefit analysts, policy makers and regulators whose goals are air pollution abatement through policy to efficiently diminish its burden on the population. Because of the wide range of groups involved there is a critical need for methods that are accurate in estimating chronic levels of PM2.5 and are both accessible and interpretable by a wide audience. It is this wide audience which we are keeping in mind in advancing methods used to estimate chronic PM2.5 levels.

Existing methods used to estimate PM2.5 levels fall in several classes that include (1) chemical transport models (CTM), (2) land use regression (LUR), (3) satellite data, and (4) different geostatistical approaches. LUR is a regression model which estimates air pollution as a function of explanatory variables. LUR takes characteristics from the study area (traffic count, road length, distance to nearest road, elevation, land cover, household density, wind, etc.) and develops a multiple linear regression model which aims at describing a pollutant of interest.5−7 Most LUR models are geared toward a model that explains the most variability of the dependent variable (i.e., the model with the highest possible r2) on a relatively small scale.8 LUR has been widely used for exposure estimation.9 Each of these methods has its distinct characteristics and corresponding utility. They range from process-based prediction methods to data-driven statistical estimation methods. The first two classes of methods are defined by their ability to predict levels based on a model representation of the processes that lead to air pollution. This is useful in estimating contributions from various emission sources. The latter two classes are driven by observations, such as satellite readings or measurement from ground monitoring stations. These are useful for obtaining estimates grounded to physical measurements of PM2.5. Although no categorization is without exception or entirely distinctive, these classes demonstrate possible methodological procedures. These four classes also differ widely in terms of accuracy, complexity, numerical cost and accessibility (see Supporting Information (SI)).

Geostatistical approaches provide, like satellite data, observationally driven estimates of PM2.5. They usually consist of linear kriging estimators of PM2.5 calculated from measurements at ground monitoring stations. These methods provide accurate estimates in the vicinity of monitoring stations and are simple to use, thereby providing a widely utilized approach. However, like any observationally driven estimation method, geostatistical methods alone cannot be used to explain contributions from major contributing sources.

While work has been done to develop methods individually within the four classes mentioned above, there is also interest in combining approaches across classes to create an estimation framework that combines the strengths of the respective groups. The goal of this work is to combine a process based method and an observationally based estimation method to create a combined estimation method that can be used by a wide audience to accurately estimate the distribution the annual PM2.5 concentration across the continental United States (U.S.) from 1999 to 2009, and to quantify how much of the estimated annual PM2.5 concentration can be explained by the major contributing sources of on road mobile emissions and stationary emissions.

We will achieve our goal by using the Bayesian Maximum Entropy (BME) knowledge synthesis framework10,11 to combine LUR with geostatistical estimation. BME utilizes Bayesian epistemic knowledge blending to combine data from multiple sources. For our process-based method we select LUR over CTMs because of its ability to use readily available information about on road mobile emissions and stationary emissions to predict annual PM2.5. For our observationally based method we rely on a geostatistical analysis of ground observations of PM2.5 concentrations because of the relatively large number of monitoring stations providing accurate measurements across the U.S. By combining methods like LUR and BME we can create a model that is numerically efficient, applicable and interpretable over a large domain size.

The knowledge base considered in the BME method consists of general knowledge describing generalizable characteristics of the space/time PM2.5 field (such as its space/time trends and dependencies, its relationship with respect to various emissions, etc), and site specific knowledge that include hard data (data without measurement error) and soft data (data with measurement errors which can be non-Gaussian). The strategy we will use in this work is to employ LUR to describe the general trends of annual PM2.5 concentrations over the entire U.S. and model the PM2.5 residuals (obtained by removing the LUR offset) using BME. This will allow us to rigorously account for the non-Gaussian uncertainty associated with annual PM2.5 concentration calculated from daily concentrations where some daily concentrations may be missing.12

One outcome of our work is the development of an LUR for the prediction of annual PM2.5 concentrations across the continental U.S., which is a geographical domain of a fairly large size. While many previous studies have developed LUR models over small geographical domains where high predictability can be achieved,13 each specific LUR model is usually only valid for the small region for which it was developed.6 In other words high predictability is achieved by sacrificing generalizability14,15 (see SI). There have been comparatively fewer studies that developed an LUR with lower predictability but higher generalizability. The LUR we present fills that knowledge gap, with a specific focus on using annual PM2.5 explained by on road mobile emissions and stationary emissions as its predictors.

Another outcome of our work is the sequential integration of two classes of methods (LUR and geostatistical) to create a combined LUR/BME estimation method that borrows strengths from each of its constituent. Combining methods is a growing research area and our work contributes to that field. While very few works have looked at combining LUR and BME approaches16,17 or LUR and kriging approaches,18 more studies are needed in order to explore the various ways by which to combine these methods. We focus specifically on using LUR to provide general knowledge about PM2.5, using BME to account for the incompleteness of daily samples, and making the combined method accessible to a wide audience. Other strategies and focus will undoubtedly have to be investigated in future works, for example creating more elaborate LUR models17 including those which use meteorological data.19

Finally we use our LUR/BME model to perform a risk assessment that differentiates the number of annual PM2.5 predicted deaths that can be explained by on road mobile emissions and stationary emissions. The dichotomous assignment of PM2.5 to these two sources allows for straightforward abatement strategies. This assessment is useful on its own to generate research questions that can improve methods used to calculate death reductions achieved under various scenarios of source reductions.

Materials and Methods

PM2.5 Data

Raw daily federally referenced method (FRM) PM2.5 monitoring data collected from 1999 to 2009 were obtained from the EPA’s Air Quality Systems (AQS) database across the contiguous United States.20 Whenever a daily PM2.5 monitoring value reported below the detection limit of its monitor, it was replaced by the mean of a log-normal distribution that was fit to all reported below-detect values. Daily values were averaged whenever two or more daily PM2.5 monitoring values were reported by collocated monitors on a given day/site.

Annual PM2.5 were calculated from daily PM2.5 monitoring values as follows: every day for which a station reported a daily PM2.5 monitoring value, a corresponding annual PM2.5 was calculated by taking the arithmetic average of all the daily monitoring values reported at that station over the previous year (i.e., 365 days) including that day. Note that this one year period could include time before January 1, 1999 (i.e., the first day for which daily monitoring data were available).

The intended sampling frequency of a given daily monitoring station was used to calculate how many daily monitoring values should have been reported in a given year period. Comparing this number to the actual number of reported monitoring values informs us about the incompleteness of intended sampling over that given year. We use this to assess the uncertainty associated with the corresponding annual PM2.5.

LUR Data

The LUR model predicts annual PM2.5 given a series of predictive LUR independent variables that characterize the effect of (a) elevation, (b) on road mobile emissions, and (c) stationary emissions. A detailed explanation of all data sources for each LUR independent variable is described in the SI.

We focus on on road mobile emissions and stationary emissions because they are two major contributors to anthropogenic pollution. For stationary emissions, we used data from the EPA’s National Emissions Inventory21 (NEI), which provides inventories of stationary emissions (in tons/year) of the main constituents of PM2.5 (i.e., SO2, NH3, PM2.5-primary and NOX). These inventories are reported in a manner that is consistent across the U.S. We assume that at space/time location p = (s, t), the effects of stationary source emissions decrease exponentially with distance between the source and the location p, as given by the equation Vi,p = ∑n = 1Nemi(en,t)exp((−3∥en – p∥)/(dri)), where, i = SO2, NH3, PM2.5, NOX, emi(en,t) is the emissions in tons/year of constituent i at stationary source emissions location en and time t and dri is the exponential decay range in km. It would be difficult to consistently and accurately measure on road mobile emissions across the entire U.S. Thus for on road mobile emissions we use data estimating vehicular traffic (annual average daily traffic counts for each major highway road segment in the U.S. as estimated through linear referencing22) and population density (people/km2) to construct variables that estimate total traffic (TT), average congestion (AC), and emission efficiency (EE) based on population density. Emission efficiency is added to correct for the assumption that every mile driven produces the same amount of emissions regardless of vehicle type by hypothesizing that areas with high population density tend to have vehicles better suited for urbanized environments, which (in general) are more fuel efficient. These traffic and emission efficiency variables are then combined to provide an estimate of on road mobile emission, thereby bypassing the laborious task of obtaining on road mobile emission data directly for a nationally sized domain.

Large Area Variability LUR Model

Our large area variability LUR expresses the annual PM2.5 at space/time location p = (s,t), where s = (s1,s2) is the spatial coordinate and t is time, as a linear combination of the corresponding LUR independent variables at p. The first independent variable consists of the elevation VElevv,p at p. The next three independent variables characterize the effect of on road mobile emissions. They are denoted as the column vector Vmobile,p = [VTT,pVAC,pVEE,p]T, where the subscript T denotes the transpose, and VTT,p, VAC,p and VEE,p are variables characterizing total traffic, average congestion, and emission efficiency, respectively, at p. The last four independent variables characterize the effect of stationary emissions. They are denoted as Vstationary,p = [VSO2,pVNH3,pVPM2.5,pVNOX,p], where VSO2,p, VNH3,p, VPM2.5,p and VNOX,p are variables charactering the concentrations of SO2, NH3, PM2.5, and NOX, respectively at space/time location p.

We consider models that include the elevation variable, at least 1 out of the 3 on road mobile emission variables, and at least 1 out of the 4 stationary emission variables, which results in a total of 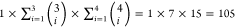Inline graphic candidate models. These models are expressed by the following equation

graphic file with name es-2013-040528_m002.jpg 1

where Zp is annual PM2.5 at p, β0 is the equation intercept, βElev, βmobile = [βTT βAC βEE] and βstationary = [βSO2 βNH3 βPM2.5 βNOX] are linear coefficients for the independent variables VElev,p, Vmobile,p and Vstationary,p, respectively, Imobile = [ITTIACIEE] and Istationary = [ISO2INH3IPM2.5INOX] are vectors of indicator values (0 or 1) such that at least one element in both Imobile and Ipoint must be 1, the “·×” operator denotes the element-by-element multiplication between same-sized vectors and εp is a homoscedastic error term.

Due to the large overlap in annual PM2.5, only a subset of annual PM2.5 was used to construct the LUR model to avoid collinearity. Namely, only the last annual PM2.5 in a calendar year was used from each station (approximately 11 000 data values), encompassing all daily values.

Each of the 105 candidate LUR models were optimized by selecting hyperparameter values that maximized the LUR r2. A hyperparameter is a physical parameter within each variable that is allowed to adjust based on predictability of annual PM2.5. Hyperparameters for annual PM2.5 include the radii ar1, ar2 and ar3 for the buffers used to calculate total traffic, average congestion, and emission efficiency, respectively, and the exponential decay ranges for stationary source variables (i.e., dri described in the SI). The fminsearch function of MATLAB was used to search for hyperparameter values that maximized the LUR r2. The search was started given an initial selection of hyperparameters described in SI.

The Akaike Information Criteria (AIC) and all variance inflation factor (VIF) values were found for each of the 105 optimized candidate LUR models. AIC is a measure of parsimony of a model and VIF is a measure of collinearity of a model. Out of the 105 optimized models, our final model has the lowest AIC value among models with VIF values <10 and with physically plausible βs. The βs have to be positive in order to be plausible, with the exception of negative βs for emission efficiency and elevation.

BME Methodology

BME is a mathematically rigorous geostatistical space/time framework developed by Christakos.10,23 BME can incorporate information from many different sources and BME is implemented using the BMElib suite of functions in MATLAB.11 The buttress of BME has been detailed in other works,11,23,24 and can be summarized as performing the following steps: (1) gathering the general knowledge base (G-KB) and site-specific knowledge base (S-KB) about the mapping situation, (2) using the Maximum Entropy principle of information theory to process the G-KB in the form of a prior probability distribution function (PDF) fG, (3) integrating S-KB using an epistemic Bayesian conditionalization rule on data fS with and without measurement error to create a posterior PDF fK, and (4) creating space/time estimates based on the analysis. We use a space/time random field (S/TRF) to describe the variability of annual PM2.5 across the U.S. Our notation a for S/TRF will consist of denoting a single random variable Z in capital letters, its realization, z, in lower case; and vectors and matrices in bold faces (e.g., Z = [Z1,...,Zn]T and z = [z1,...,zn]T). Let Z(p) = Z(s,t) be a space/time random field (S/TRF) representing annual PM2.5.

We define the transformation of the PM2.5 data zh observed at locations ph as

graphic file with name es-2013-040528_m003.jpg 2

where oZ(p) may be any deterministic offset that can be calculated without error as a function of the space/time coordinate p. We then define X(p) as the S/TRF representing the variability and uncertainty associated with the transformed data xh, and we let Z(p) = X(p)+oZ(p) be the S/TRF representing PM2.5.

In this work, we consider two choices for oZ(p): (1) a constant value and (2) the LUR estimate ẑLUR,P given by

graphic file with name es-2013-040528_m004.jpg 3

where the estimated Îs indicators and β̂s coefficients are those derived in our final annual PM2.5 LUR model. We can then calculate ẑk, the estimated annual PM2.5 at unmonitored location pk by obtaining the BME estimate x̂k for the transformed S/TRF X(p) at the estimation point pk, and adding back oz(pk), the offset calculated at pk.

The G-KB for the transformed S/TRF X(p) consists of its expected value mx(p) and covariance function cX(p,p′) (see SI).

The S-KB for X(p) consists of hard and soft data. The hard data xh = zh – oZ(ph) are obtained based on annual PM2.5 values zh calculated at hard data points ph where at least 75% of intended samples were collected, in line with EPA regulations pertaining to valid design values.25 Data points not meeting this completeness criterion are classified as the soft data points ps, with an uncertainty attributed to the incompleteness of intended sampling. Following Akita et al,12 the uncertainty associated with the annual PM2.5, zs for station i and date t is described by a Gaussian PDF truncated below zero, with mean μi,t and standard deviation σi,t. The mean μi,t is simply the sample mean of the ni,t daily concentrations (zi,j, j = 1,...,ni,t) recorded at station i over 1 year preceding date t. The epistemic uncertainty associated with the incompleteness of intended sampling is characterized by the difference between ni,t and the intended number of samples ni* ≥ ni,t that would have been collected if the station worked as intended in accordance with the monitor’s sampling frequency. Therefore a reasonable choice for the standard deviation quantifying that uncertainty is

graphic file with name es-2013-040528_m005.jpg 4

where the first factor is the standard deviation of the sample mean and the second factor is a population correction factor that accounts for the incompleteness of intended sampling from a population of size ni*. The PDF for xs is then derived from the PDF for zs by simply using the transformation xs = zs – oz(ps).

The G-KB and S-KB for the S/TRF X(p) can overall be written as G = {mX(p),cX(p,p′)} and S = {xh, fS (xS)}, and in this case the BME posterior PDF for X(pk) at estimation point pk is given by fK(xk) = A–1 ∫ dxfS(xS) fG(x) where x = (xk,xh,xs) is a realization of X at points p = (pk, ph, ps) and A is a normalization constant.10,25 Finally the PDF for zk is obtained by simply using the back-transformation zk = xk + oz(pk).

Comparison of Methods Using Cross-Validation Analysis

In order to test the estimation improvement of LUR and BME, a cross-validation was performed to compare three different methods used in this study: (a-constant/hard) setting the deterministic global (i.e., covering a substantial domain where variability within the domain can be largely diverse) offset oZ(p) to a constant value and considering all data as hard, (b-LUR/hard) setting the global offset to the LUR model and considering all data as hard and (c-LUR/hard and soft) setting the global offset to the LUR predicted value and considering data as hard and soft as defined in the previous section. For each of these methods, the cross validation procedure consists of randomly selecting 20 000 hard data points, removing each one at a time, and re-estimating it from the remaining annual PM2.5. The cross-validation statistics investigated include mean squared estimation error (MSE), root mean squared estimation error (RMSE), mean absolute estimation error (MAE), mean of the root variance of the posterior PDFs (MR), the square of Pearson’s correlation coefficient, and the square of Spearman’s correlation coefficient. Equations for each measure are defined in the SI. Along with the leave-one-out cross validation (LOOCV) of 20, 000 hard data point, a 10-fold spatial cross-validation was also performed.

Risk Assessment Application

The incorporation of the LUR model into the BME methodology has many potential applications including determining the mortality of various diseases attributable to PM2.5. Excess mortality was calculated using the methodology presented by Li,26 assuming linearity, in order to quantify total mortality, mortality from ischemic heart disease (IHD) and mortality from lung cancer (LC). Relative risks for these diseases were obtained from Krewski et al.27 Deaths at the county level were obtained from the CDC.28 Excess deaths were calculated for (1) annual PM2.5, (2) annual PM2.5 explained by on road mobile emissions, and (3) annual PM2.5 explained by stationary emissions.

Let ẑl (p) denote our estimate of annual concentrations, where l = total for total PM2.5, l = mobile for PM2.5 explained by on road mobile emissions, and l = stationary for PM2.5 explained by stationary emissions. For l = total we simply use ẑtotal (p) = ẑLUR/BME,p, where ẑLUR/BME,(p) is the LUR/BME estimate of annual PM2.5 described earlier. For l = mobile we use the LUR in a relative manner to estimate the ratio αLUR mobile(p) = ((Îmobile ·× β̂mobile)Vmobile,p)/(ẑLUR,p) corresponding to the proportion of PM2.5 that the LUR model explains from on road mobile emissions. We then multiply that ratio with the LUR/BME estimate of annual PM2.5, so that ẑmobile(p) = ẑLUR/BME,pαLUR mobile(p). Likewise we use ẑstationary(p) = ẑLUR/BME,pαLUR stationary(p, with αLUR stationary(p) = ((Îstationary ·× β̂stationary)Vstationary,p)/(ẑLUR,p)). The mortality for a specific cause of death (e.g., total mortality, IHD, LC) attributed to an annual concentration ẑl (p) is given by Li et al.26

graphic file with name es-2013-040528_m006.jpg 5

where I0 is the baseline incidence rate for the cause of death of interest, β is the corresponding concentration response coefficient, P is the population at the county level, and zb is the background concentration. Sources have suggested a background level in the U.S. for PM2.5 of 3–5 μg/m3.29 We use zb = 5 μg/m3.

Results

Annual PM2.5

There were 1 478 149 annual PM2.5 data points from 1999 to 2009 coming from 1576 monitoring stations. These include 406 962 (27.53%) soft data points. The mean of the annual PM2.5 is 12.44 μg/m3, the variance is 11.57(μg/m3)2, the skewness is 0.56 and the kurtosis is 5.57. The minimum annual value is 1.63 μg/m3 and the maximum annual value is 75.40 μg/m3.

Large Area Variability LUR Model

The final LUR model had six independent variables: elevation, three on road mobile emission variables (total traffic, average congestion, emission efficiency), and two stationary emission variables (NH3 and SO2) (Table 1). Table 1 describes the optimal hyperparameters for each variable along with their corresponding β̂ values. This LUR model has an r2 = 0.53, providing generalizable predictability of annual PM2.5 over the entire U.S. from 1999 to 2009.

Table 1. Hyperparameters and Corresponding β for the Final LUR Model.

final LUR model
variable range (km) β̂ (μg/m3 per variable unit)
intercept NA 7.54 × 1000
elevationa 0 –8.87 × 10–04
total trafficb 694 3.04 × 10–03
average congestionc 33 2.54 × 10–05
emission efficienyd 730 –1.76 × 10–02
SO2e 210 1.10 × 10–04
NH3e 11.5 1.49 × 10–06
Open in a new tab
a

Meters.

b

km driven/km2.

c

km driven/km.

d

People/km2.

e

Thousand tons/year.

LUR/BME Model

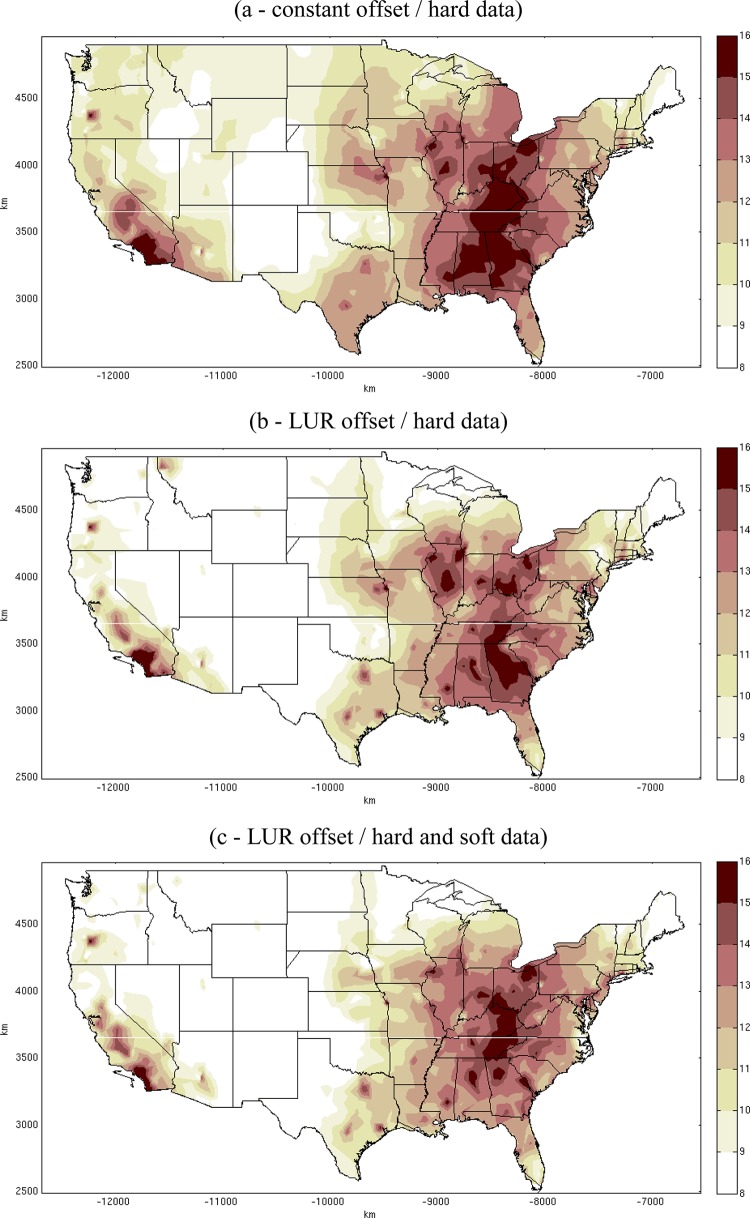
The combination of the LUR and BME methods through methods (a) to (c) led to a refined estimation of annual PM2.5 as seen in Figure 1 showing estimated levels across the U.S. for May 1, 1999. Method (a-constant/hard) using a constant offset and using all data as hard does not differentiate well the annual PM2.5 across southern California and estimates fairly benign levels for several states west of the Mississippi river. By incorporating the LUR offset, method (b-LUR/hard) provides estimates of annual PM2.5 that are more refined and localized. By further incorporating the soft data to the hard data and LUR offset, method (c-LUR/hard and soft) further refines the description of hot spots across the country. Method (c) is able to pick up finer scale variation in concentrations compared to methods (a) and (b). This finer scale variation can also be seen in subsequent months (SI Figure S5).

Figure 1.

Figure 1

Open in a new tab

BME predicted annual PM2.5 (μg/m3) concentration estimation map across the contiguous U.S. on May 1, 1999 for the following methods: (a) constant offset/hard data; (b) LUR offset/hard data; and (c) LUR offset/hard and soft data.

Cross validation statistical measures indicated a consistent improvement in mapping accuracy from method (a) to (c) (Table 2). Measures of estimations errors (MSE, RMSE, MAE, MR) decreased from method (a) to (b) and from method (b) to (c), while measures of correlation (Square Pearson’s Corr. Coeff. and Square Spearman Corr. Coeff.) increased from method (a) to (b) and from method (b) to (c). Incorporating the LUR offset while using only hard data (i.e., going from method (a) to (b)) resulted in a reduction of 21.89% in MSE. Further incorporating soft data (i.e., going from method (b) to (c)) resulted in an additional reduction of 4.87% in MSE. The reduction in MSE from method (b) to (c) is more pronounced when performing cross-validation on points that contain a higher percentage of soft data (SI Table S3). This reduction is more pronounced still when estimation neighborhoods around cross-validation locations are forced to have soft data points (SI Table S4).

Table 2. Cross Validation Statistical Measures and Percent Change for Three Estimation Methods.

method LUR only (a) constant/hard (b) LUR/hard (c) LUR/hard and soft % change from (a) to (b) % change from (b) to (c)
MSEa 7.04 1.69 1.32 1.26 –21.89 –4.87
RMSEb 2.65 1.30 1.15 1.12 –11.62 –2.46
MAEb 1.97 0.79 0.63 0.63 –20.73 –0.45
MRb 1.86 1.87 1.12 1.07 –40.25 –4.08
Square Pearson’s Corr.c 0.50 0.68 0.87 0.88 28.94 0.78
Square Spearman’s Corr.c 0.55 0.67 0.89 0.89 32.13 0.32
Open in a new tab
a

[μg/m3]2.

b

μg/m3.

c

Unitless.

The r2 correlation (Square Pearson’s Corr. Coeff.) changes from 0.88 for the LOOCV to 0.78 for the 10-fold cross validation. This corresponds to 12.8% shrinkage in r2, which is reasonable since the training set for the 10-fold cross validation is substantially smaller than that of the LOOCV.

Risk Assessment

Using eq 5 with ẑtotal(p) we find that the number of deaths from 1999 to 2007 predicted from annual PM2.5 exposure in excess of background levels is 905 560. These results were validated using the EPA’s BenMAP program30 and are consistent with other estimates.31

We then used eq 5 with ẑmobile(p) (PM2.5 explained by on road mobile emissions) and ẑstationary(p) (PM2.5 explained by stationary emissions). The mean of the ẑmobile(p) across all the space/time data points is 3.4 μg/m3, while the mean of ẑstationary(p) across the same points is only 1.15 μg/m3. Accordingly the number of deaths attributed to PM2.5 explained by on road mobile emissions is greater than the number of deaths attributed to PM2.5 explained by stationary emissions (Table 3). For instance, the number of deaths attributed to PM2.5 explained by on road mobile emissions is 568 090 from 1999 to 2007, which is 1.85 times more than the 306 316 deaths attributed to PM2.5 explained by stationary emissions. Similarly, on road mobile emissions explained 1.86 times the number of IHD deaths and 1.98 times the number of LC deaths compared to deaths explained by stationary emissions. The number of deaths assumes that the relative risk used in eq 5 can be applied to the entire population and that estimated ambient concentration is a surrogate for exposure. This risk assessment does not incorporate the varying toxicity of PM2.5.

Table 3. Death Counts Predicted from Annual PM2.5 Explained by on Road Mobile and Stationary Emissions.

  predicted from on road mobile emissions predicted from stationary emissions
1999–2007 all cause mortality 568 090 306 316
1999–2007 ischemic heart disease deaths 415 163 223 341
1999–2007 lung cancer deaths 85 044 43 035
Open in a new tab

This finding is interesting because, according to the NEI, primary PM2.5, NO2, SO2, and NH3 coming from on road mobile emissions sum up to 70 834 thousand tons from 1999 to 2007 while primary PM2.5, NO2, SO2, and NH3 coming from stationary emissions sum up to 293 446 thousand tons for the same time period (SI Table S2). Hence, even though on road mobile emissions emit only about a quarter of the mass emitted by stationary emissions, the number of deaths predicted from PM2.5 explained by on road mobile emissions is almost twice that predicted from PM2.5 explained by stationary emissions.

Discussion

The first major outcome of our work is the creation of a global LUR model that predicts large area variability of PM2.5 across the entire contiguous United States from 1999 to 2009. Only a handful of studies have developed LUR models that can be classified as “general” in that they produced results generalizable to domain sizes as large as ours (SI Figure S1). Although the LUR may perform better in some areas than others, the model is “generalizable” in a relative fashion when compare to LUR models developed over a smaller domain. To the best of our knowledge, the closest LUR models developed over such a large domain size are Hart et al.15 and Beelen et al.14 for annual PM10, and Beckerman et al.17 for monthly PM2.5.

The Hart et al.15 and Beelen et al.14 studies developed regression models to predict annual PM10 concentrations across the United States from 1985 to 2000 and across 15 European countries for 2001, respectively. Even though their models differed (i.e., the Hart et al.15 model used traffic related variables while the Beelen et al.14 model used meteorology and land use), they produced similar r2 of 49% and 41%, respectively. These studies provided substantial contribution to the literature on annual PM10. However, there is a lack of comparable global models for PM2.5. Our study is successful in helping to fill that knowledge gap by providing a general LUR for PM2.5 that achieves an r2 of 53% that is comparable or better than that for annual PM10.

Of the limited general LUR models developed for the long-term average concentration of PM2.5, the LUR-without-remote-sensing model developed by Beckerman et al.17 is the most comparable to ours. The explanatory variables of that model are traffic within 1km and green space within 0.1km. The r2 of that model was 3% for their training data set and 5% for their validation data set. This provides a substantial contribution to the literature because it describes the small area variability at a scale of 0.1–1km which is attributable to primary PM2.5 emitted as ultrafine particles and specific metals that are responsible for a large portion of observed health impacts.17 Hence their relatively small r2 of 3–5% makes sense since on road emission of primary PM2.5 makes up only a small fraction of annual PM2.5. By contrast, our explanatory variables capture the large area variability of PM2.5, as demonstrated by our hyperparameter values ranging from ten to hundreds of km (Table 1). These values are characteristic of the transport of secondary PM2.5 over long distances. Hence our model describes the large area variability of secondary PM2.5. Since the majority of PM2.5 comes from secondary formation, it makes sense that our model achieves a higher r2 (53%) than that of Beckerman et al.17 (3–5%). Therefore their model describes short-area variability due to the local effect of traffic coming from primary PM2.5, while our model describes the large area variability of PM2.5 due to the long-range effect of secondary PM2.5 created from on road mobile emissions and stationary emissions. To the best of our knowledge no other LUR models have predicted the large area variability of secondary PM2.5 and our model is the first to address this important knowledge gap. Our LUR model estimated PM2.5 coming from on road mobile emissions using TT, AC, and EE. However, due to the complex nature of PM2.5, these variables may capture other sources outside of on road mobile emissions. We hypothesized that EE using population density corrects for over prediction of on road mobile emissions coming from TT and AC. Indeed, out of the 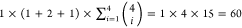Inline graphic models that had the EE variable, βEE was positive for the 1 × (1 + 1 + 0) × 15 = 30 models where EE appears without TT and it consistently switched to being negative for the 1 × (0 + 1 + 1) × 15 = 30 models that contain both the EE and the TT variable. This suggests that EE alone is a surrogate for on road mobile emissions. However, when paired with the TT traffic variable, EE corrects the overestimation of these variables. This finding is in agreement of our hypothesis and therefore supports the conclusion that population density can be used as a surrogate for increased EE of the vehicle fleet. Obtaining accurate estimates of on road mobile emissions along all roads is a difficult task. By using population data to calculate EE, we facilitate this task and as a result we ensure the accessibility of our model to a wider audience.

While previous LUR models represent important contributions to the field, our model differs in several important ways: (1) our model describes large area variability of PM2.5, which characterizes the secondary component of this pollutant, (2) the explanatory variables are constructed from data that are easily obtainable by a wide audience and (3) our model allows to distinguish between PM2.5 explained by on road mobile emissions and PM2.5 explained by stationary emissions. To our knowledge this is one of the first LUR models to capture secondary PM2.5 using easily obtainable explanatory variables describing on road mobile emissions and stationary emissions.

The second major outcome of this work is the combination of our LUR model with BME to create a combined LUR/BME hybrid estimation method for annual PM2.5. In this hybrid approach, LUR is used as a first step to characterize global trends in PM2.5 and BME is used to extract unexplained variability in the residuals. Our results (Table 2) demonstrate that LUR/BME is successful at combining the strengths of each of its component methods. Indeed, LUR/BME results in a 21.89% reduction in MSE and a 28.94% increase in r2 over BME alone, which is itself more accurate than LUR alone. The population correction factor presented in the soft data variance in eq 4 does not account for the fact that annual PM2.5 averages are correlated in time. As well, the number of daily values within a year ni,t does not account for the seasonality of missing values.

Others have combined LUR/BME such as Beckerman et al. Their work saw an r2 of 0.79 using a validation data set comprised of about 10% of the data. By comparison we achieved an r2 of 0.78 using a 10-fold cross validation, where each of validation points had similar distance-to-closest-monitor as those of Beckerman et al. A key difference between our works is that we extended their work by incorporating non-Gaussian soft data that rigorously accounted for the uncertainty associated with the incompleteness of daily samples. Our r2 indicates that our model was successful in this novel incorporation of non-Gaussian soft data in the LUR/BME framework, which resulted in one of the most accurate LUR/BME estimations to date of annual PM2.5 as supported by the fact that our r2 is similar to that of Beckerman et al. A unique strength of our model is that these highly accurate LUR/BME estimates of annual PM2.5 can be separated into the portions explained by on road mobile emissions and stationary emissions, which to our knowledge had not been done before to a similar level of precision.

Building on the novel contributions of the first two outcomes of our work, an important third outcome of this work is a risk assessment of annual PM2.5 exposure explained from major contributing sources. Estimating annual PM2.5 is useful for assessing long-term exposure needed to investigate chronic diseases. Others have already used LUR estimates in epidemiological studies.32−35 From 1999 to 2007 there were 568 090 deaths attributed to PM2.5 explained by 70 834 thousand tons of primary PM2.5, NO2, SO2, and NH3 emitted by on road mobile emissions, which correspond to a ratio of 8.02 deaths/thousand tons for on road mobile emissions. By contrast there were 306 316 deaths attributed PM2.5 explained by 293 446 thousand tons of primary PM2.5, NO2, SO2, and NH3 emitted by stationary emissions, which correspond to a ratio of 1.04 deaths/thousand tons for stationary emissions. These results are informative because they imply that mechanisms involved in the creation and long-range transport of secondary PM2.5 lead to substantially differing health impacts depending on whether emissions originate from on road mobile emissions or stationary emissions.

Other works have also examined excess mortality due to current emissions levels. When investigating Massachusetts power plants Levy and Spengler36 found that current power plant emissions in the surrounding area that emitted above the best available control technology (BACT) resulted in approximately 70 deaths per year in a ∼ 600 km by 600 km region which includes areas of Massachusetts and New York where the power plants were located. According to the BACT of 3 lb/MWh of SO2 and 1.5 lb/MWh of NOX, there would be a reduction of 43 951 tons of SO2 and 4376 tons of NOX from the two power plants mentioned in the study. This would result in 1.34 deaths/thousand tons of SO2 and 2.51 deaths/thousand tons of NOX due to power plants emissions in the area being above the BACT. That work used the CTM CALPUFF in which emission levels can be zeroed out while our work uses an LUR model which measures annual predicted PM2.5. Levy only investigated power plants while our work looked at major contributing sources. Even though LUR cannot be directly compared to CTMs, our LUR results are useful in a relative manner as they allow us to contrast on road mobile emissions and stationary emissions which have not been done before.

In order to reduce the number of deaths due to PM2.5 exposure, our results indicate a reduction in one ton of on road mobile emissions would be eight times more beneficial than a one ton reduction in stationary emissions. This may be accomplished though any number of actions such as increased accessibility and reliance on public transportation in areas of high population density to more stringent emission standards that would further promote fuel efficiency.

Acknowledgments

This research was supported in part by a grant from the National Institute of Environmental Health Sciences (T32ES007018).

Supporting Information Available

Further explanation of estimation methods, LUR domain sizes, independent variables, covariance models, BME equations, cross-validation statistics and cross-validation results. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

es4040528_si_001.pdf (1MB, pdf)

References

  1. Pope C. A.; Ezzati M.; Dockery D. W. Fine-particulate air pollution and life expectancy in the United States. N. Engl. J. Med. 2009, 3604376–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Boldo E.; Medina S.; LeTertre A.; Hurley F.; Mücke H.-G.; Ballester F.; Aguilera I.; Eilstein D. Apheis: Health impact assessment of long-term exposure to PM2.5 in 23 European cities. Eur. J. Epidemiol. 2006, 216449–58. [DOI] [PubMed] [Google Scholar]
  3. Pope C. A. III; Burnett R. T.; Thurston G. D.; Thun M. J.; Calle E. E.; Krewski D.; Godleski J. J. Cardiovascular mortality and long-term exposure to particulate air pollution: Epidemiological evidence of general pathophysiological pathways of disease. Circulation 2004, 109171–7. [DOI] [PubMed] [Google Scholar]
  4. Cohen A. J.; Anderson H. R.; Ostro B.; Pandey K. D.; Krzyzanowski M.; Kunzli N.; Gutschmidt K.; Pope A.; Romieu I.; Samet J. M.; Smith K. The global burden of disease due to outdoor air pollution. J. Toxicol. Environ. Health, Part A 2005, 6813–141301–7. [DOI] [PubMed] [Google Scholar]
  5. Briggs D. J.; Collins S.; Elliott P.; Fischer P.; Kingham S.; Lebret E.; Pryl K.; Reeuwijk H. V. A. N.; Smallbone K.; van der Veen A. Mapping urban air pollution using GIS: A regression-based approach. Int. J. Geogr. Inf. Sci. 1997, 117699–718. [Google Scholar]
  6. Poplawski K.; Gould T.; Setton E.; Allen R.; Su J.; Larson T.; Henderson S.; Brauer M.; Hystad P.; Lightowlers C.; Keller P.; Cohen M.; Silva C.; Buzzelli M. Intercity transferability of land use regression models for estimating ambient concentrations of nitrogen dioxide. J. Exposure Sci. Environ. Epidemiol. 2009, 191107–117. [DOI] [PubMed] [Google Scholar]
  7. Jerrett M.; Arain M. A.; Kanaroglou P.; Beckerman B.; Crouse D.; Gilbert N. L.; Brook J. R.; Finkelstein N.; Finkelstein M. M. Modeling the intraurban variability of ambient traffic pollution in Toronto, Canada. J. Toxicol. Environ. Health, Part A 2007, 703–4200–12. [DOI] [PubMed] [Google Scholar]
  8. Mavko M. E.; Tang B.; George L. A. A sub-neighborhood scale land use regression model for predicting NO2. Sci. Total Environ. 2008, 3981–368–75. [DOI] [PubMed] [Google Scholar]
  9. Ryan P. H.; Lemasters G. K. A review of land-use regression models for characterizing intraurban air pollution exposure. Inhalation Toxicol. 2007, 19Suppl 1127–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Christakos G.Modern Spatiotemporal Geostatistics; Oxford University Press: New York, 2000. [Google Scholar]
  11. Christakos G.; Bogaert P.; Serre M. L.. Temporal GIS: Advanced Functions for Field-Based Applications; Springer: New York, 2002. [Google Scholar]
  12. Akita Y.; Chen J.-C.; Serre M. L. The moving-window Bayesian maximum entropy framework: Estimation of PM2.5 yearly average concentration across the contiguous United States. J. Expos. Sci. Environ. Epidemiol. 2012, 225496–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Mölter A.; Lindley S.; Vocht F. De; Simpson A.; Agius R. Science of the Total Environment Modelling air pollution for epidemiologic research—Part II: Predicting temporal variation through land use regression. Sci. Total Environ. 2010, 4091211–217. [DOI] [PubMed] [Google Scholar]
  14. Beelen R.; Hoek G.; Pebesma E.; Vienneau D.; Hoogh K. De; Briggs D. J. Mapping of background air pollution at a fine spatial scale across the European Union. Sci. Total Environ. 2009, 40761852–67. [DOI] [PubMed] [Google Scholar]
  15. Hart J. E.; Yanosky J. D.; Puett R. C.; Ryan L.; Dockery D. W.; Smith T. J.; Garshick E.; Laden F. Spatial modeling of PM10 and NO2 in the continental United States, 1985–2000. Environ. Health Perspect. 2009, 117111690–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Yu H.; Wang C.; Liu M.; Kuo Y. Estimation of fine particulate matter in Taipei using landuse regression and bayesian maximum entropy methods. Int. J. Environ. Res. Public Health 2011, 862153–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Beckerman B.; Jerrett M.; Martin R. V; Lee S.; Donkelaar A. Van; Ross Z.; Su J.; Burnett R. A hybrid approach to estimating national scale spatiotemporal variability of PM2.5 in the contiguous United States. Environ. Sci. Technol. 2013, 47137233–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ross Z.; Jerrett M.; Ito K.; Tempalski B.; Thurston G. D. A land use regression for predicting fine particulate matter concentrations in the New York City region. Atmos. Environ. 2007, 41112255–2269. [Google Scholar]
  19. Su J. G.; Brauer M.; Ainslie B.; Steyn D.; Larson T.; Buzzelli M. An innovative land use regression model incorporating meteorology for exposure analysis. Sci. Total Environ. 2008, 3902–3520–529. [DOI] [PubMed] [Google Scholar]
  20. U.S. EPA. Air Quality System. Research Triangle Park, NC: http://www.epa.gov/ttn/airs/airsaqs/ (accessed September 11, 2010). [Google Scholar]
  21. U.S. EPA. National Emissions Inventory. Research Triangle Park, NC: http://www.epa.gov/ttn/chief/eiinformation.html (accessed January 26, 2011). [Google Scholar]
  22. FHWA HPMS http://www.fhwa.dot.gov/ohim/hpmsmanl/hpms.htm (accessed February 3, 2009).
  23. Christakos G. A Bayesian/maximum-entropy view to the spatial estimation problem. Mathe. Geol. 1990, 227763–777. [Google Scholar]
  24. Serre M. L.; Christakos G. Modern geostatistics: Computational BME analysis in the light of uncertain physical knowledge - the Equus Beds study. Stochastic Environ. Res. Risk Assess. 1999, 1311–26. [Google Scholar]
  25. De Nazelle A.; Arunachalam S.; Serre M. L. Bayesian maximum entropy integration of ozone observations and model predictions: An application for attainment demonstration in North Carolina. Environ. Sci. Technol. 2010, 44155707–5713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li Y.; Gibson J. M.; Jat P.; Puggioni G.; Hasan M.; West J. J.; Vizuete W.; Sexton K.; Serre M. Burden of disease attributed to anthropogenic air pollution in the United Arab Emirates: Estimates based on observed air quality data. Sci. Total Environ. 2010, 408235784–93. [DOI] [PubMed] [Google Scholar]
  27. Krewski D.; Jerrett M.; Burnett R. T.; Ma R.; Hughes E.; Shi Y.; Turner M. C.; Pope C. A.; Thurston G.; Calle E. E.; Thun M. J.. Extended Follow-up and Spatial Analysis of the American Cancer Society Study Linking Particulate Air Pollution and Mortality; Health Effects Institute, 2009; Vol. 140, pp 5–114. [PubMed] [Google Scholar]
  28. Centers for Disease Control and Prevention. National Center for Health Statistics. Compressed Mortality File 1999–2007. http://wonder.cdc.gov/cmf-icd10.html (accessed January 11, 2012).
  29. Ostro B.Outdoor air pollution: Assessing the environmental burden of disease at national and local levels. In WHO Environmental Burden of Disease Series No. 5; World Health Organization, 2004. [Google Scholar]
  30. Abt Associates, Inc. Model Attainment Test Software (Version 2), Bethesda, MD; Prepared for U.S. Environmental Protection Agency Office of Air Quality Planning and Standards: Research Triangle Park, NC. , 2010; http://www.epa.gov/air/benmap/. [Google Scholar]
  31. Fann N.; Lamson A. D.; Anenberg S. C.; Wesson K.; Risley D.; Hubbell B. J. Estimating the national public health burden associated with exposure to ambient PM2.5 and ozone. Risk analysis 2012, 32181–95. [DOI] [PubMed] [Google Scholar]
  32. Wilhelm M.; Ghosh J. K.; Su J.; Cockburn M.; Jerrett M.; Ritz B.. Traffic-related air toxics and preterm birth: A population-based case-control study in Los Angeles County, California. Environ. Health 2011, 10 (89). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Gehring U.; Eijsden M. V.; Dijkema M. B. A.; Van Der Wal M. F.; Fischer P.; Brunekreef B. Traffic-related air pollution and pregnancy outcomes in the Dutch ABCD birth cohort study. Occup. Environ. Med. 2011, 68136–43. [DOI] [PubMed] [Google Scholar]
  34. Ryan P. H.; Lemasters G. K.; Biswas P.; Levin L.; Hu S.; Lindsey M.; Bernstein D. I.; Lockey J.; Villareal M.; Hershey G. K. K.; Grinshpun S. A. A comparison of proximity and land use regression traffic exposure models and wheezing in infants. Environ. Health Perspect. 2007, 1152278–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ryan P. H.; Lemasters G. K.; Levin L.; Burkle J.; Biswas P.; Hu S.; Grinshpun S.; Reponen T. A land-use regression model for estimating microenvironmental diesel exposure given multiple addresses from birth through childhood. Sci. Total Environ. 2008, 4041139–147. [DOI] [PubMed] [Google Scholar]
  36. Levy J. I.; Spengler J. D.; Hlinka D.; Sullivan D.; Moon D. Using CALPUFF to evaluate the impacts of power plant emissions in Illinois: Model sensitivity and implications. Atmos. Environ. 2002, 3661063–75. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

es4040528_si_001.pdf (1MB, pdf)

Articles from Environmental Science & Technology are provided here courtesy of American Chemical Society

RESOURCES