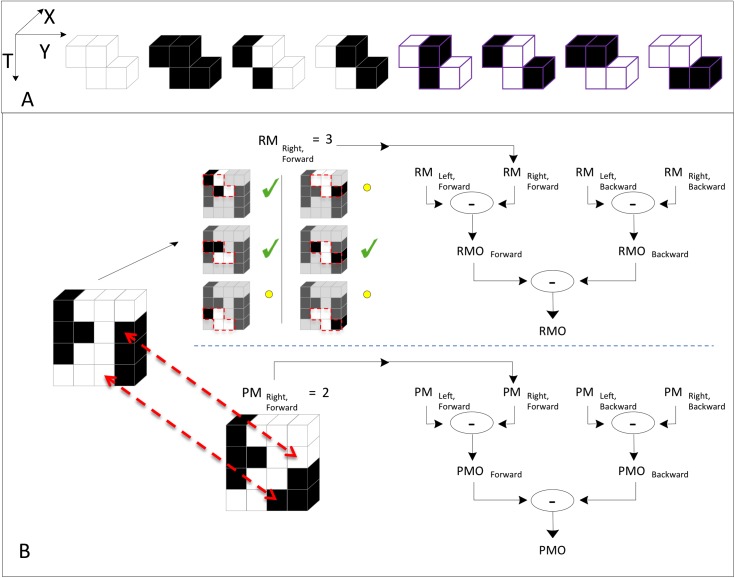
Figure 2.

A summary of calculation of the RMO and PMO local scores in a spatiotemporal ROI, using NF-S motion as an example; further details are in the text. (A) The library of eight template colorings consistent with NF-S motion. Note that all colorings have an even number of black checks. (The four rightmost colorings, marked in purple, are the templates used for pure NF-S, as the two-check F templates that they contain are inconsistent with F motion.) (B) Calculation of RMO and PMO scores for a 1×4×4 spatiotemporal ROI. For the RMO method (top), we consider all placements of the template within the ROI. There are six such placements (red dashes), and we tally the placements that yield colorings contained in the library of panel A, as these are the placements in which the black and white checks are consistent with NF-S motion. Checkmarks indicate the placements that result in colorings that are within the library; circles indicate the placements that result in colorings that are not in the library. Tallying the number of placements in the library yields a unidirectional RM motion score (in this case, right forward). Analogous scores are calculated by reversing the NF-S template in space (left forward) and time (right backward, left backward). These four unidirectional RM scores are combined in an opponent calculation to yield the RMO score for the ROI. For the PMO method (bottom) the entire ROI is treated as a whole. We determine the fewest number of checks that must be changed so that every placement of the template within the ROI yields a coloring that is in the library of panel A. In this case, changing two checks suffices: When these two checks are flipped in contrast (dashed arrows), all glider placements are in the library, and the resulting ROI is entirely consistent with NF-S motion. The tally of these changes yields the right, forward unidirectional PM signal. These four unidirectional PM signals are combined by an opponent computation to yield the PMO score for the ROI.