Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Apr 30.
Published in final edited form as: J Neurosci Methods. 2014 Feb 11;227:75–82. doi: 10.1016/j.jneumeth.2014.02.003

An investigation of fMRI time series stationarity during motor sequence learning foot tapping tasks

Othman Muhei-aldin a, Jessie VanSwearingen b, Helmet Karim c, Theodore Huppert c, Patrick J Sparto b, Kirk I Erickson d, Ervin Sejdić a,*
PMCID: PMC3987746  NIHMSID: NIHMS567744  PMID: 24530436

Abstract

Background:

Understanding complex brain networks using functional magnetic resonance imaging (fMRI) is of great interest to clinical and scientific communities. To utilize advanced analysis methods such as graph theory for these investigations, the stationarity of fMRI time series needs to be understood as it has important implications on the choice of appropriate approaches for the analysis of complex brain networks.

New Method:

In this paper, we investigated the stationarity of fMRI time series acquired from twelve healthy participants while they performed a motor (foot tapping sequence) learning task. Since prior studies have documented that learning is associated with systematic changes in brain activation, a sequence learning task is an optimal paradigm to assess the degree of non-stationarity in fMRI time-series in clinically relevant brain areas. We predicted that brain regions involved in a “learning network” would demonstrate non-stationarity and may violate assumptions associated with some advanced analysis approaches. Six blocks of learning, and six control blocks of a foot tapping sequence were performed in a fixed order. The reverse arrangement test was utilized to investigate the time series stationarity.

Results:

Our analysis showed some non-stationary signals with a time varying first moment as a major source of non-stationarity. We also demonstrated a decreased number of non-stationarities in the third block as a result of priming and repetition.

Comparison with Existing Methods:

Most of the current literature does not examine stationarity prior to processing.

Conclusions:

The implication of our findings is that future investigations analyzing complex brain networks should utilize approaches robust to non-stationarities, as graph-theoretical approaches can be sensitive to non-stationarities present in data.

Keywords: functional magnetic resonance imaging, time series, stationarity, reverse arrangement test, foot tapping

1. Introduction

Investigating brain networks involved in complex cognitive, affective, or motor tasks are of great interest from scientific and clinical perspectives. To define brain networks, researchers have used various experimental modalities such as structural and functional magnetic resonance imaging (MRI) (Dale and Halgren, 2001), (Smith et al., 2004), (Friston et al., 1996), positron emission tomography (PET) (Friston et al., 1996), diffusion tensor imaging (Dale and Halgren, 2001), magnetoencephalography (Bilodeau et al., 1997), and electroencephalography (Jeong et al., 2001). The most common modality is fMRI, first shown in 1992 to be useful for exploring functional brain activity (Le Bihan, 2003). Since then, fMRI has been widely used to study brain networks involved in a variety of psychological and motor behaviors using several signal processing approaches (Dale and Halgren, 2001), (Smith et al., 2004), (Friston et al., 1996), (Bilodeau et al., 1997), (Jeong et al., 2001). MRI has enabled us to understand the brain macroscopic organization by enabling us to study the structural and functional networks (Guye et al., 2010). The use of fMRI to study brain activation patterns has several advantages over other methods such as PET, which requires radioactive ligands to be injected into the participants. fMRI: (1) is considered a non-invasive technology for acquiring brain images, (2) can be used to examine task performance in less time, acquiring scan images more rapidly than the PET, and (3) the scans have high spatial resolution (Dale et al., 2000). The blood oxygenation and flow is the fundamental basis for fMRI. Thus the brain activation signal increases around the area of blood vessels and brain tissues with higher blood oxygenation levels and blood flow (Friston et al., 1996), (Ogawa et al., 1990), (Vink et al., 2007); the more activated brain regions have higher blood flow and blood oxygenation than non-active regions (Friston et al., 1996), (Ogawa et al., 1990), (Vink et al., 2007). Hence, the measured signal by fMRI depends on the change of oxygenation which is referred to as the Blood Oxygen Level Dependent (BOLD) signal (Ogawa et al., 1990), (Poldrack et al., 2011).

The vast majority of recent contributions on complex brain networks are based largely on graph theory analysis (Bullmore and Sporns, 2009). The graph theoretical analysis of MRI data has been widely used to understand both normal brain networks and dysfunctional brain networks resulting from pathologies such as Alzheimer’s disease (Guye et al., 2010), (He et al., 2008), (Hu et al., 2013), (Buckner et al., 2009), schizophrenia (Guye et al., 2010), (Lynall et al., 2010), (van den Heuvel et al., 2010), stroke (Guye et al., 2010), (He et al., 2007), epilepsy (Guye et al., 2010), (Vlooswijk et al., 2011) and tumors (Guye et al., 2010). For example, Buckner et al. (Buckner et al., 2009) were able to demonstrate a correlation between the site of the targeted regions and the location of major hubs in Alzheimer’s disease. He et al. (He et al., 2008) have also shown different structural variation of brain small-world organization in individuals with Alzheimer’s disease, which has been shown to accurately classify people with Alzheimer’s disease. Similarly, Liu et al. (Liu et al., 2008) have shown the network properties in individuals with schizophrenia relative to controls.

In addition to understanding dysfunctional networks in pathological conditions, the brain networks involved in affect regulation, motor control and execution, and learning and memory are important for understanding normal brain development and function. Hence, researchers have used graph theoretical approaches to examine learning-related changes in network connectivity (Sami and Miall, 2013). In order to establish a brain network using modern graph theory, there are a number of steps to be taken (Bullmore and Sporns, 2009), (Rubinov and Sporns, 2010), (Reijneveld et al., 2007): (1) define the network nodes, (2) estimate association/correlation between nodes, (3) compile pairwise associations between nodes and generate an association matrix, and (4) calculate the network characteristics. All of these steps require a choice of a suitable approach in order to obtain an adequate network representation. Yet, despite this emerging literature, many researchers using graph theoretical approaches for fMRI data have not closely examined whether their data violate the assumptions of graph-theory. In particular, in order to make an informed decision regarding the analytical approach we need to first understand whether the fMRI time series are stationary, i.e., if the statistical properties such as mean and variance of a time series are time-invariant (Chatfield, 2003). The assumption of fMRI stationarity is especially important in the second step to understand whether the choice of an analytical approach needs to be robust to non-stationarities. Furthermore, the stationarity of fMRI time series is relevant when discussing simple meaningful statistics of fMRI time series such as means, variances, and correlations. These statistics are more useful as a description of the data if the time-series is stationary (Brockwell and Davis, 2009), (Shumway and Stoffer, 2010). The stationarity is also relevant to the frequency analysis of the fMRI time series as the Fourier transform is suitable for stationary signals (Beck et al., 2006). In this work, we used reverse arrangement analysis to quantify the degree of non-stationarity in fMRI data in the context of network connectivity. Such investigation will help us define the most appropriate approaches that should be considered in the establishment of connectivity matrices and complex brain networks.

2. Time series and stationarity

A set of observations recorded at a specific time is usually denoted as a time series (Brockwell and Davis, 2009). If the observations are recorded continuously with time, then we say it is a continuous time series. On the other hand, if x(n) denotes observations made within time interval 0 ≤ n ≤ N−1, where N represents the length of the signal, then x(n) is a discrete time series since the observations are made at time intervals from the discrete set γ. This time series can be considered as a realization of random variables {Xn, n ∈ γ} (Brockwell and Davis, 2009). Stationarity is either strong stationarity (strict stationarity) or weak (wide sense) stationarity. If the statistical properties of a time series are time-invariant, then this time series is said to have strict stationarity (Chatfield, 2003), i.e.:

FXn1,…,Xnk(x1,x2,…,xN)=FXn1+h,…,Xnk+h(x1,x2,…,xn) (1)

for all positive integers h and for all (n1, … , nk) ∈ ℤ. In other words, strict stationary time series should express similar statistical properties in the graphs of two equal-length time interval of realization (Brockwell and Davis, 2009). A time series is considered to have weak or (wide-sense) stationarity if the only first two moments are time-invariant (Shumway and Stoffer, 2010), such that the mean is constant, i.e.,

E(Xn1)=E(Xn1+h) (2)

and the covariance only depends on the time lag between two observations (Brockwell and Davis, 2009), i.e.,

Cov(Xn1,Xn2)=Cov(Xn1+h,Xn2+h) (3)

A usual first in the time series analysis is the visual inspection of the series in order potentially determine suitable analysis methods and/or statistical variables beneficial for summarizing information contained in the series (Shumway and Stoffer, 2010).

To understand which mathematical approaches should be adopted, we need to understand the stationarity of the time series (Manuca and Savit, 1996). To examine the time series stationarity, one of the following non-parametric tests is applied: a run test, a reverse arrangement test (RAT), or a modified RAT (Beck et al., 2006). The RAT is a non-parametric test that has often been used to evaluate the wide-sense stationarity of a time series (Bendat and Piersol, 2000), (Alves and Chau, 2008), especially to investigate the weak stationarity of physiological and biomedical signals (Bilodeau et al., 1997), (Alves and Chau, 2008), (Hampson et al., 2005), (Harris et al., 1993), (Nhan and Chau, 2009), (Novak et al., 1996). Basically, the RAT test is used to search for monotonic trends in the mean square values calculated within non-overlapping intervals of a particular time series signal of interest (Bendat and Piersol, 2000), (Chau et al., 2005). In this study we performed the RAT test. Below are the steps we took to use the RAT test to examine the stationarity of the fMRI motor sequence learning task-related brain activation signal pattern.

  1. A time series is divided into M equal non-overlapping segments. The number of segments M can be determined using the following equation:
    M=NL (4)
    where N is the length of the time series and L is the desired segment length.
  2. Calculate the square mean value Y(k) for each segment:
    Y(k)=1L∑i=kL(k+1)L−1x2(i)for0≤k≤M−1 (5)
  3. The total number of reverse arrangements A is then counted within the sequence of mean square values Y0, Y1, … , YM−1. A reverse arrangement occurs when the square mean value of one segment is greater than the mean square values of the subsequent segment, i.e. when: Ya > Yb for a < b. Hence, using this condition, Yk will form the indicator:
    s(k,d)={1ifY(k)>Y(K+d)0otherwise} (6)
    For 1 < d ≤ D, where D = M−k−1; and therefore, for kth time step, the reverse arrangement test is given by:
    A(k)=∑d=1Ds(k,d) (7)
    and the total number of reverse arrangement test A is given by:
    AT=∑k=0M−1A(k) (8)
  4. The calculated value of the total reverse arrangement AT from the previous step is then compared to the value that would be expected from a realization of a weakly stationary random process. If we considered the sample as weakly stationary, then the expected value of A has a normal distribution (Bendat and Piersol, 2000) with the mean given by:
    μT=L(L−1)4 (9)
    and the variance:
    σT2=L(L−1)(2L+5)72 (10)

The null hypothesis that Yk is weakly stationary is rejected if the calculated AT falls outside the critical values defined by a significance level α. In this research, the critical values were determined from the calculation of the stationarity test statistic ZT, which is given by:

ZT=AT−μTσT (11)

where ZT ~ N(0,1), and the critical values of ZT at the significant level α can be defined as Z1−α/2 and Zα/2, where Z is a standard normal variate. At 5% significance level, the values of Z are given by Z1−α/2 = −1.96 and Zα/2 = 1.96; and the values of the test statistics ZT will have one of the following possibilities:

  • Zα/2 < ZT < Z1−α/2: the null hypothesis that the time series is wide sense or weakly stationary is accepted.

  • ZT ≥ Z1−α/2: this means that the number of reverse arrangements is greater than that expected of a stationary signal. This implies an existence of downtrend in the mean square sequence.

  • ZT ≤ Zα/2: this means that the number of reverse arrangements is less than that expected of a stationary signal. This implies an existence of an upward trend in the mean square sequence.

3. Methodology

3.1. Participants

Twelve (6 males and 6 females) healthy young adult participants (age range from 19 to 48 years old, mean age 33 years old) participated in this experiment approved by the Institutional Review Board at the University of Pittsburgh. A written informed consent was obtained from all participants after the nature of the experiment had been explained. All participants were right handed.

3.2. Data acquisition

Data acquisition was conducted by an expert fMRI technician from the Department of Radiology, University of Pittsburgh, Pittsburgh, PA. The MRI scanning was acquired on a 3T Siemens TRIO scanner using a 12-channel parallel receive head coil. GE-EPI BOLD (FA=90 deg; TR=2000 ms; TE=29 ms) scans were collected with thirty-eight axial slices (3.4 mm thickness) with a 3.4 mm × 3.4 mm in-plane resolution (64×64). A T2-weighted structural scan (FA=150 deg, TR=3000 ms, TE=11/101 ms) with voxel size 10.30 × 31.0 × 31.0 mm (matrix 256×224×256) was used to acquire 48 slices covering the whole brain which was collected prior to the functional scans. Head movement was minimized during the experiment by placing pillows around the head within the head coil.

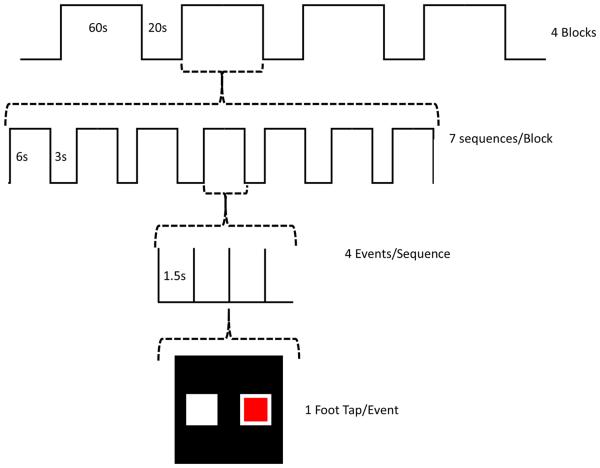
Each of the 60 second blocks consisted of a series of 7 tapping sequences as shown in Figure 1.

Figure 1.

Figure 1

Open in a new tab

A flowchart depicting the fMRI protocol of the experiment.

Each sequence consisted of 4 directed movements (e.g. 7 sequences/block × 4movements/sequence = 28 total movements/block). For the control blocks, 7 random tapping sequences were presented with no repeats. For the learning blocks, an identical tapping sequence was repeated 7 times. Each learning block used a different sequence so that each learning block required relearning the sequence. For each movement, participants were presented with a red box either on the left or right side of a display screen mounted at the head of the MR scanner, which was viewed using a mirror affixed above the head coil. Participants were told to perform ankle plantar flexion (foot tap) with either the right or left foot depending on if the box appeared on the right or left side, respectively. During the control sequence, the pattern of foot tapping was random and subjects were not expected to learn the sequence. During the learning sequence, subjects also repeated the same sequence 7 times per 60 second block; thus they were expected to learn the pattern, as demonstrated by a decrease in foot tap onset latencies. Participants were instructed to simply perform the foot tapping task as indicated by the position of the red box projected on the screen. They were not informed that the intent was to study motor sequence learning. An overall diagram of the experimental sequence is shown in Figures 2 and 3.

Figure 2.

Figure 2

Open in a new tab

A diagram showing the experimental sequence in learning process.

Figure 3.

Figure 3

Open in a new tab

A diagram showing the experimental sequence in control process.

3.3. Data preprocessing

The Statistical Parametric Mapping (SPM) toolbox was utilized to preprocess and analyze the acquired fMRI data (Poldrack et al., 2011). Data preprocessing steps included: realignment or (motion correction), coregistration, normalization, and smoothing. The realignment is performed using the least square method and a six parameter spatial transformation (Freire et al., 2002). The movement artifacts and excessive head motion in the fMRI scans was removed in this procedure using a well known approach (Liu et al., 2008). Next, the mean functional image generated from the previous realignment step is co-registered to a high resolution anatomical image and all of the other functional images are then resliced to align with the reference image. To normalize the scans between different subjects, we utilized the standard template image in MNI space (Montreal Neurological Institute) (Vink et al., 2007). Unlike the rigid body realignment to correct for motion, normalization includes changing the size of the brain to match the size and position of the template. Hence, smoothing is performed to: increase the signal to noise ratio, increase inter-subject overlap, and to increase the validity of the analysis. Smoothing includes blurring the functional MRI images using a Gaussian filter (i.e data is convolved with a Gaussian kernel) (Braver et al., 1997). After smoothing the images, each voxel becomes a weighted region of interest (ROI, the voxels under the kernel). The size of the new voxel can be obtained using the full width half maximum technique (FWHM) (Friston et al., 1996), which is an indication of the distribution of the kernel values. Ideally, the FWHM kernel size should be chosen to match the size of the expected activation

After the scans were processed and registered with the MNI template image, the scans were all segmented into 90 cortical and subcortical anatomical ROIs using the MarsBAR toolbox (Brett et al., 2002). The mean time series for each of the 90 regions of interest (ROIs) were computed by averaging all voxels within each region at each time point in the time series, resulting in 170 data points for each of the 90 anatomical ROIs. Since the human brain has two cerebral hemispheres, the 90 regions are divided equally between the left and the right hemisphere, i.e. 45 ROIs in each hemisphere. This was done by using the Automated Anatomical Labeling template (AAL) (Tzourio-Mazoyer et al., 2002). Cerebellum regions were not included as the fMRI scans did not cover these regions.

3.4. Data Analysis

The data analysis consisted of the fMRI scans from three different runs of foot tapping sequences for each of the 12 participants. The first and the third runs were acquired while the participants performed the foot tapping sequences of the learning-control-learning-control set. The second run was acquired while the participants performed foot tapping task in the order of the control-learning-control-learning set. Using the acquired images, we extracted 90 time series of length 170 data points for each participant.

Next, we used the RAT to investigate the stationarity of the fMRI time series. At an increment of one, we tested stationarity at various window sizes (10 to 15 scans) for each time series. The window size selection is based on a window that will maintain enough data points to estimate a single statistical parameter for the calculation of both the mean squared value within each interval and the total number of reverse arrangements (Chau et al., 2005). The null hypothesis of time invariance was then tested at 5% level of significance. For time-varying time series, we utilized a regression analysis to identify whether the time series had a varying mean and/or variance. Furthermore, we identified the mean and variance as either having an increasing or decreasing trend at the 5% significance level.

4. Results

4.1. Effects of window size

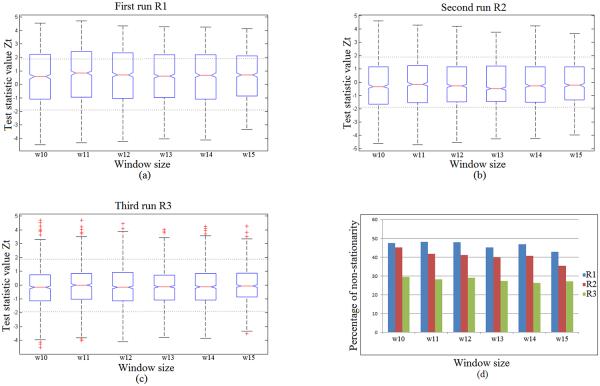
Once the 170 data points had been processed, we computed 90 fMRI time series that have been used for stationarity testing using the RAT Test. It can be clearly seen from Figure 4 (a)-(d) below that the greatest percentage of non-stationary signals were distinguished during the first and second runs of the fMRI task, while the least number of non-stationary signals were found within the last run.

Figure 4.

Figure 4

Open in a new tab

The effect of window size on the stationarity test statistic, ZT, during the foot tapping task: first run R1 (a), second run R2 (b), and third run R3 (c); and the effect of window size on the percentage of non-stationary time series identified for each of the three runs (R1 = run-1, R2 = run-2, R3 = run-3) respectively (d). R1 and R3 are motor learning set runs; R2 is a control set run.

The impact of a window size on stationarity is depicted in Figure 4(d). The percentage of non-stationary time series decreased with increasing window size; but this effect is not statistically significant due to a few window size increments (p > 0.75). At larger window sizes, a time series is divided into fewer segments and fewer comparisons between subsequent mean square values are carried out. This process will reduce the number of opportunities to detect a reverse arrangement. The boxplots on the other hand show the stationarity of the test statistics value ZT at different window sizes for the three runs. In each of the three sub-figures, the two horizontal dashed lines represent the boundary between stationarity and non-stationarity of the data based on the value of ZT defined by |Z| < 1.96.

From the boxplots in Figure 4 (a)-(c), we can observe the following:

  • The fMRI time series were generally stationary since the median values of the stationary test statistic ZT fell within the stationarity range at the 5% significance level previously defined and represented by the two dashed lines at each figure ; i.e. |Z| < 1.96.

  • It can be also noticed from the first and last runs R1 and R3, which have the same task sequence, that only in the last run R3 the 25% and 75% of the ZT values fell within that range. For the first run R1, only the 25 percentile fell within the range. In each run (R1,R2 and R3) as shown in Figure 4, the number of stationary time series tended to increase with increasing window size.

  • With increasing window size, the variation in the stationary statistic remains relatively constant as shown in Figure 4. Therefore, an intermediate value of 13 points is utilized for further analysis.

4.2. Sources of non-stationarity

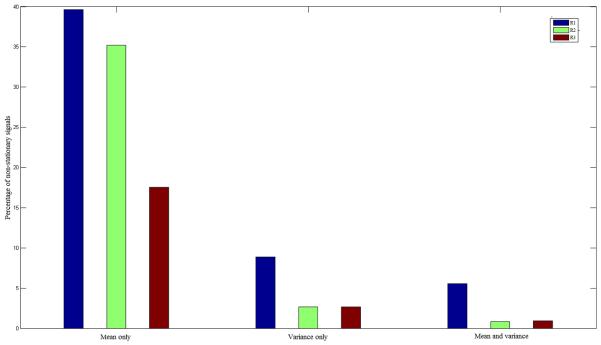
As defined at the beginning of this paper a time series is said to be strictly stationary if its statistical properties are time-invariant. We investigated the sources of non-stationarity using the intermediate window size 13. It can be noticed that the last time course will be trimmed from every time series because of the indivisibility of time series lengths on the window size. We then calculated the mean and variance for each segment and tested for a significant linear regression relationship. What we observed from the extracted fMRI signals as shown in Figure 5 is that the non-stationarities can be mostly attributed to a change in the mean value over time. Furthermore, very few signals experiences time-dependant variance alone, and fewer signals demonstrated both non-stationary means and variances.

Figure 5.

Figure 5

Open in a new tab

Sources contributing to non-stationarity time series as a percentage of non-stationary time series identified within each foot tapping task run: R1 = run 1, R2 = run 2, R3 = run 3.

Based on our observation, non-stationarity was found in different brain regions rather in specific brain regions. However, the regions that were seen stationarity among all participants are listed in Table 1.

Table 1.

Stationary regions among all participants.

Region Name Location on Hemisphere
Amygdala left hemisphere
Caudate left hemisphere
Caudate right hemisphere
Medial Orbitofrontal Gyrus left hemisphere
Insula right hemisphere
Olfactory left hemisphere
Inferior Parietal Gyrus right hemisphere
Superior Parietal Gyrus left hemisphere
Precuneus left hemisphere
Supramarginal Gyrus left hemisphere
Middle Temporal Gyrus left hemisphere
Superior Temporal Pole left hemisphere
Superior Temporal Gyrus left hemisphere
Open in a new tab

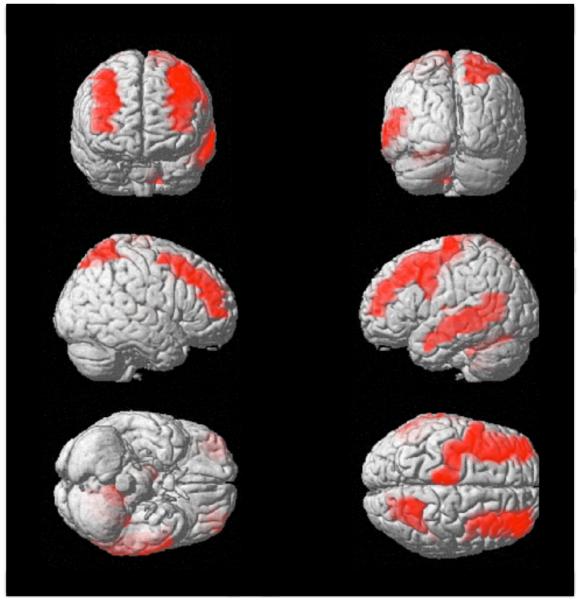
These regions are illustrated in Figure 6. The intensity of colors in the image does not reflect the amount or the percentage of stationarity/non-stationarity but rather reflects depth of the region in the brain. So the regions that are deep in the brain have low intensities, whereas the regions that are closer to the cortex have a higher intensity.

Figure 6.

Figure 6

Open in a new tab

Brain regions found stationary in all participants. Brain images are shown in the sequence: Front-Back, Right-Left, Bottom-Top.

5. Discussion

The human brain has been viewed as one of the most complicated physiological networks (Stam and Reijneveld, 2007). Researchers try to understand how brain networks respond and interact to different stimuli using neuroimaging techniques. Our investigation informed us about the suitability of potential signal processing tools to be used to evaluate and establish the complex brain functional networks and connectivity matrices. To establish such connectivity matrices and analyze them, we need to utilize graph-theoretical approaches which have been shown to provide a powerful new way to quantify and analyze brain structural and functional networks (Bullmore and Sporns, 2009). Such tools were initially applied to fMRI time series (Dodel et al., 2002), as a way to identify functional clusters of activated brain regions during a finger tapping task. Since then, the graph theory has become a leading approach to analyze brain networks when researchers were also able to find strong and significant correlations between locally and distant (intra- and inter-hemispheric) brain regions (Stam and Reijneveld, 2007). However, one of the first steps in utilizing the graph-theoretical approaches is to compute a measure of correlation among the considered brain regions. Previous studies utilized cross-correlation (Siegle et al., 2007), cross-coherence (Sun et al., 2004), and mutual information (Jeong et al., 2001) among others. However, given that some fMRI time series are non-stationary, approaches resistant to non-stationarities should be considered (e.g., wavelets (Bullmore et al., 2004), (Daubechies, 1990), (Achard and Bullmore, 2007)).

We observed fewer non-stationarities in R3 than in R1, even-though the signal was acquired under the same stimuli and the same experimental procedure. This could be interpreted as a result of “priming” a phenomenon defined as “a change in the speed, bias or accuracy of the processing of a stimulus, following prior experience with the same, or a related, stimulus” (Henson, 2003). The implicit memory phenomenon, known as direct or repetition priming, has been considered as one of the three different categories of priming (Schacter, 1992). From the brain activation point of view, implicit memory captures the effect of previous experience on the current experiment, even in the absence of conscious awareness of the past (Henson, 2003), (Graf et al., 1984), (Milner et al., 1968), (Hauptmann and Karni, 2002), (Warrington and Weiskrantz, 1974). Moreover, repetition can also be another main reason of decreased brain activation and blood flow level in the repeated task R3. Neural activity usually decreases for repeating stimuli (Grill-Spector et al., 2006). In particular, Gruber and Muller have discussed the repetition priming task using electroencephalogram technology (Gruber and Müller, 2005) by analyzing the induced gamma band activity during the repetition of familiar and unfamiliar line drawings. Penhune and Doyon have also discussed such phenomenon and revealed a dynamic network of motor structures which have different activation during different phases of learning and repetition. They have shown that the recall of motor sequences in humans is mediated predominantly by cortical networks which suggest the involvement of cerebellar mechanisms in the early learning procedures. These cerebellar mechanisms are no longer recalled or involved in the repeated tasks (Penhune and Doyon, 2002).

Repetition suppression has also been observed using fMRI and PET technologies; referred to as the “response suppression phenomenon” (Desimone, 1996) or “decremental responses” (Brown and Xiang, 1998). Processing a stimuli more than once will produce what is called the “sharpening phenomenon” of the stimuli’s cortical representation. This can be explained as some of the neurons that processed and coded the stimuli at the beginning will exhibit a lower response in the repeated task showing “a response suppression phenomenon.” The lower response from the previous neurons decreases the mean firing rate of a neuron population resulting in a decrease in the captured fMRI signal (Henson, 2003).

6. Conclusion

In this paper, we have successfully investigated the stationarity of fMRI time series in 12 healthy participants while they performed motor sequence learning foot tapping tasks in three different runs. We found that stationarity and non-stationarity were not concentrated or found in specific brain regions so that further analysis and interpretation can be introduced. We showed that some of the extracted time series are non-stationary, primarily in the form of time-varying mean. The finding reported in this study provide a new insight into what approach should be considered prior to establishing the connectivity matrices. Our results have implications for future studies as researchers should utilize techniques robust for non-stationarities.

  • fMRI time series are analyzed using various signal processing approaches.

  • Critical to understand whether fMRI time series are (non)stationary.

  • We showed that fMRI time series can be nonstationary.

  • Our findings will aid a proper choice of analysis methods.

Acknowledgment

This work was supported in part by the Pittsburgh Claude D. Pepper Older Americans Independence Center (NIA P30 AG 024827). We would also like to thank the Pittsburgh Claude D. Pepper Older Americans Independence Center Neuroimaging Working Group for development of the MR compatible force platform.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Computational Biology. 2007;3(2):e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alves N, Chau T. Stationarity distributions of mechanomyogram signals from isometric contractions of extrinsic hand muscles during functional grasping. Journal of Electromyography and Kinesiology. 2008;18(3):509–515. doi: 10.1016/j.jelekin.2006.11.010. [DOI] [PubMed] [Google Scholar]
  3. Beck TW, Housh TJ, Weir JP, Cramer JT, Vardaxis V, Johnson GO, Coburn JW, Malek MH, Mielke M. An examination of the runs test, reverse arrangements test, and modified reverse arrangements test for assessing surface EMG signal stationarity. Journal of Neuroscience Methods. 2006;156(1):242–248. doi: 10.1016/j.jneumeth.2006.03.011. [DOI] [PubMed] [Google Scholar]
  4. Bendat JS, Piersol AG. Random data analysis and measurement procedures. Measurement Science and Technology. 2000;11(12):1825. [Google Scholar]
  5. Bilodeau M, Cincera M, Arsenault AB, Gravel D. Normality and stationarity of EMG signals of elbow flexor muscles during ramp and step isometric contractions. Journal of Electromyography and Kinesiology. 1997;7(2):87–96. doi: 10.1016/s1050-6411(96)00024-7. [DOI] [PubMed] [Google Scholar]
  6. Braver TS, Cohen JD, Nystrom LE, Jonides J, Smith EE, Noll DC. A parametric study of prefrontal cortex involvement in human working memory. Neuroimage. 1997;5(1):49–62. doi: 10.1006/nimg.1996.0247. [DOI] [PubMed] [Google Scholar]
  7. Brett M, Anton J-L, Valabregue R, Poline J-B. Region of interest analysis using the marsbar toolbox for SPM 99. Neuroimage. 2002;16:S497. [Google Scholar]
  8. Brockwell PJ, Davis RA. Time series: theory and methods. Springer. 2009 [Google Scholar]
  9. Brown M, Xiang J-Z. Recognition memory: Neuronal substrates of the judgement of prior occurrence. Progress In Neurobiology. 1998;55(2):149–189. doi: 10.1016/s0301-0082(98)00002-1. [DOI] [PubMed] [Google Scholar]
  10. Buckner RL, Sepulcre J, Talukdar T, Krienen FM, Liu H, Hedden T, Andrews-Hanna JR, Sperling RA, Johnson KA. Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. The Journal of Neuroscience. 2009;29(6):1860–1873. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bullmore E, Fadili J, Maxim V, Șendur L, Whitcher B, Suckling J, Brammer M, Breakspear M. Wavelets and functional magnetic resonance imaging of the human brain. Neuroimage. 2004;23:S234–S249. doi: 10.1016/j.neuroimage.2004.07.012. [DOI] [PubMed] [Google Scholar]
  12. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews Neuro-science. 2009;10(3):186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
  13. Chatfield C. Vol. 59. Chapman and Hall/CRC; 2003. The analysis of time series: an introduction. [Google Scholar]
  14. Chau T, Chau D, Casas M, Berall G, Kenny DJ. Investigating the stationarity of paediatric aspiration signals. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2005;13(1):99–105. doi: 10.1109/TNSRE.2004.841384. [DOI] [PubMed] [Google Scholar]
  15. Dale AM, Halgren E. Spatiotemporal mapping of brain activity by integration of multiple imaging modalities. Current Opinion in Neuro-biology. 2001;11(2):202–208. doi: 10.1016/s0959-4388(00)00197-5. [DOI] [PubMed] [Google Scholar]
  16. Dale AM, Liu AK, Fischl BR, Buckner RL, Belliveau JW, Lewine JD, Halgren E. Dynamic statistical parametric mapping: combining fMRI and EMG for high-resolution imaging of cortical activity. Neuron. 2000;26(1):55–67. doi: 10.1016/s0896-6273(00)81138-1. [DOI] [PubMed] [Google Scholar]
  17. Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory. 1990;36(5):961–1005. [Google Scholar]
  18. Desimone R. Neural mechanisms for visual memory and their role in attention. Proceedings of the National Academy of Sciences. 1996;93(24):13494–13499. doi: 10.1073/pnas.93.24.13494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dodel S, Herrmann JM, Geisel T. Functional connectivity by cross-correlation clustering. Neurocomputing. 2002;44:1065–1070. [Google Scholar]
  20. Freire L, Roche A, Mangin J-F. What is the best similarity measure for motion correction in fMRI time series? IEEE Transactions on Medical Imaging. 2002;21(5):470–484. doi: 10.1109/TMI.2002.1009383. [DOI] [PubMed] [Google Scholar]
  21. Friston KJ, Holmes A, Poline J-B, Price CJ, Frith C. Detecting activations in PET and fMRI: Levels of inference and power. Neuroimage. 1996;4(3):223–235. doi: 10.1006/nimg.1996.0074. [DOI] [PubMed] [Google Scholar]
  22. Graf P, Squire LR, Mandler G. The information that amnesic patients do not forget. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10(1):164. doi: 10.1037//0278-7393.10.1.164. [DOI] [PubMed] [Google Scholar]
  23. Grill-Spector K, Henson R, Martin A. Repetition and the brain: neural models of stimulus-specific effects. Trends in Cognitive Sciences. 2006;10(1):14–23. doi: 10.1016/j.tics.2005.11.006. [DOI] [PubMed] [Google Scholar]
  24. Gruber T, Müller MM. Oscillatory brain activity dissociates between associative stimulus content in a repetition priming task in the human EEG. Cerebral Cortex. 2005;15(1):109–116. doi: 10.1093/cercor/bhh113. [DOI] [PubMed] [Google Scholar]
  25. Guye M, Bettus G, Bartolomei F, Cozzone PJ. Graph theoretical analysis of structural and functional connectivity MRI in normal and pathological brain networks. Magnetic Resonance Materials in Physics, Biology and Medicine. 2010;23(5-6):409–421. doi: 10.1007/s10334-010-0205-z. [DOI] [PubMed] [Google Scholar]
  26. Hampson KM, Munro I, Paterson C, Dainty C. Weak correlation between the aberration dynamics of the human eye and the cardiopulmonary system. Journal of the Optical Society of America A. 2005;22(7):1241–1250. doi: 10.1364/josaa.22.001241. [DOI] [PubMed] [Google Scholar]
  27. Harris GF, Riedel SA, Matesi D, Smith P. Standing postural stability assessment and signal stationarity in children with cerebral palsy. IEEE Transactions on Rehabilitation Engineering. 1993;1(1):35–42. [Google Scholar]
  28. Hauptmann B, Karni A. From primed to learn: the saturation of repetition priming and the induction of long-term memory. Cognitive Brain Research. 2002;13(3):313–322. doi: 10.1016/s0926-6410(01)00124-0. [DOI] [PubMed] [Google Scholar]
  29. He BJ, Snyder AZ, Vincent JL, Epstein A, Shulman GL, Corbetta M. Breakdown of functional connectivity in frontoparietal networks underlies behavioral deficits in spatial neglect. Neuron. 2007;53(6):905–918. doi: 10.1016/j.neuron.2007.02.013. [DOI] [PubMed] [Google Scholar]
  30. He Y, Chen Z, Evans A. Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer’s disease. The Journal of Neuroscience. 2008;28(18):4756–4766. doi: 10.1523/JNEUROSCI.0141-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Henson R. Neuroimaging studies of priming. Progress in Neurobiology. 2003;70(1):53–81. doi: 10.1016/s0301-0082(03)00086-8. [DOI] [PubMed] [Google Scholar]
  32. Hu C, Cheng L, Sepulcre J, Fakhri G, Lu YM, Li Q. A graph theoretical regression model for brain connectivity learning of Alzheimer’s disease. Int. Symp. on Biomedical Imaging. 2013 [Google Scholar]
  33. Jeong J, Gore JC, Peterson BS. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clinical Neurophysiology. 2001 May;112(5):827–835. doi: 10.1016/s1388-2457(01)00513-2. [DOI] [PubMed] [Google Scholar]
  34. Le Bihan D. Looking into the functional architecture of the brain with diffusion MRI. Nature Reviews Neuroscience. 2003;4(6):469–480. doi: 10.1038/nrn1119. [DOI] [PubMed] [Google Scholar]
  35. Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T. Disrupted small-world networks in schizophrenia. Brain. 2008;131(4):945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
  36. Lynall M-E, Bassett DS, Kerwin R, McKenna PJ, Kitzbichler M, Muller U, Bullmore E. Functional connectivity and brain networks in schizophrenia. The Journal of Neuroscience. 2010;30(28):9477–9487. doi: 10.1523/JNEUROSCI.0333-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Manuca R, Savit R. Stationarity and nonstationarity in time series analysis. Physica D: Nonlinear Phenomena. 1996;99(2):134–161. [Google Scholar]
  38. Milner B, Corkin S, Teuber H-L. Further analysis of the hippocampal amnesic syndrome: 14-year follow-up study of HM. Neuropsychologia. 1968;6(3):215–234. [Google Scholar]
  39. Nhan B, Chau T. Infrared thermal imaging as a physiological access pathway: A study of the baseline characteristics of facial skin temperatures. Physiological Measurement. 2009;30(4):N23. doi: 10.1088/0967-3334/30/4/N01. [DOI] [PubMed] [Google Scholar]
  40. Novak V, Honos G, Schondorf R. Is the heart emptyat syncope? Journal of the Autonomic Nervous System. 1996;60(1):83–92. doi: 10.1016/0165-1838(96)00040-9. [DOI] [PubMed] [Google Scholar]
  41. Ogawa S, Lee T, Kay A, Tank D. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences. 1990;87(24):9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Penhune VB, Doyon J. Dynamic cortical and subcortical networks in learning and delayed recall of timed motor sequences. The Journal of Neuroscience. 2002;22(4):1397–1406. doi: 10.1523/JNEUROSCI.22-04-01397.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Poldrack RA, Mumford JA, Nichols TE. Handbook of Functional MRI Data Analysis. Cambridge University Press; 2011. [Google Scholar]
  44. Reijneveld JC, Ponten SC, Berendse HW, Stam CJ. The application of graph theoretical analysis to complex networks in the brain. Clinical Neurophysiology. 2007;118(11):2317–2331. doi: 10.1016/j.clinph.2007.08.010. [DOI] [PubMed] [Google Scholar]
  45. Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage. 2010;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  46. Sami S, Miall RC. Graph network analysis of immediate motor-learning induced changes in resting state BOLD. Frontiers in Human Neuroscience. 2013;7 doi: 10.3389/fnhum.2013.00166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Schacter DL. Priming and multiple memory systems: Perceptual mechanisms of implicit memory. Journal of Cognitive Neuroscience. 1992;4(3):244–256. doi: 10.1162/jocn.1992.4.3.244. [DOI] [PubMed] [Google Scholar]
  48. Shumway RH, Stoffer DS. Time Series Analysis and its Applications. Springer Science+ Business Media. 2010 [Google Scholar]
  49. Siegle GJ, Thompson W, Carter CS, Steinhauer SR, Thase ME. Increased amygdala and decreased dorsolateral pre-frontal BOLD responses in unipolar depression: Related and independent features. Biological Psychiatry. 2007 Jan;61(2):198–209. doi: 10.1016/j.biopsych.2006.05.048. [DOI] [PubMed] [Google Scholar]
  50. Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
  51. Stam CJ, Reijneveld JC. Graph theoretical analysis of complex networks in the brain. Nonlinear Biomedical Physics. 2007;1(1):3. doi: 10.1186/1753-4631-1-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sun FT, Miller LM, D’Esposito M. Measuring interregional functional connectivity using coherence and partial coherence analyses of fMRI data. NeuroImage. 2004 Feb;21(2):647–658. doi: 10.1016/j.neuroimage.2003.09.056. [DOI] [PubMed] [Google Scholar]
  53. Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
  54. van den Heuvel MP, Mandl RC, Stam CJ, Kahn RS, Pol HEH. Aberrant frontal and temporal complex network structure in schizophrenia: a graph theoretical analysis. The Journal of Neuroscience. 2010;30(47):15915–15926. doi: 10.1523/JNEUROSCI.2874-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Vink M, Raemaekers M, van der Schaaf A, Mandl R, Ramsey N. Pre-processing and analysis. 2007 [Google Scholar]
  56. Vlooswijk M, Vaessen M, Jansen J, de Krom M, Majoie H, Hofman P, Aldenkamp A, Backes W. Loss of network efficiency associated with cognitive decline in chronic epilepsy. Neurology. 2011;77(10):938–944. doi: 10.1212/WNL.0b013e31822cfc2f. [DOI] [PubMed] [Google Scholar]
  57. Warrington EK, Weiskrantz L. The effect of prior learning on subsequent retention in amnesic patients. Neuropsychologia. 1974;12(4):419–428. doi: 10.1016/0028-3932(74)90072-4. [DOI] [PubMed] [Google Scholar]

RESOURCES