Likelihood-based inference in isolation-by-distance models using the spatial distribution of low-frequency alleles

Abstract

Estimating dispersal distances from population genetic data provides an important alternative to logistically-taxing methods for directly observing dispersal. While methods for estimating dispersal rates between a modest number of discrete demes are well developed, methods of inference applicable to “isolation-by-distance” models are much less established. Here we present a method for estimating ρσ², the product of population density (ρ) and the variance of the dispersal displacement distribution (σ²). The method is based on the assumption that low-frequency alleles are identical by descent. Hence, the extent of geographic clustering of such alleles, relatively to their frequency in the population, provides information about ρσ². We show that a novel likelihood-based method can infer this composite parameter with a modest bias in a lattice model of isolation-by-distance. For calculating the likelihood, we use an importance sampling approach to average over the unobserved intra-allelic genealogies, where the intra-allelic genealogies are modeled as a pure birth process. The approach also leads to a likelihood ratio test of isotropy of dispersal, i.e. whether dispersal distances on two axes are different. We test the performance of our methods using simulations of new mutations in a lattice model and illustrate its use with a data set from Arabidopsis thaliana.

Introduction

Patterns of dispersal have long been recognized as important for evolutionary and ecological dynamics. Nevertheless, accurately quantifying patterns of dispersal via direct observation is difficult in most systems. Instead, patterns of genetic variation can be used to obtain indirect estimates of dispersal tendencies (Slatkin, 1987). For models in which individuals are in distinct demes, a variety of indirect methods are available, for example, cladistic methods (Slatkin and Maddison, 1989; Excoffier et al., 1992) and likelihood-based methods (Rannala and Hartigan, 1995; Tufto et al., 1996; Beerli and Felsenstein, 2001; Nielsen and Wakeley, 2001; Iorio et al., 2005; Hey and Nielsen, 2007).

In comparison, methods for estimating dispersal in continuous isolation-by-distance (CIBD) models are less well developed. In CIBD models, individuals are distributed across a continuous habitat and mate preferentially with nearby individuals. If an individual is born at a location (x₀, y₀) then the probability distribution of the location where it leaves its offspring is assumed to be a continuous distribution that is time invariant, identical for every individual, and of the form k(x−x₀, y−y₀) where k(·, ·) is a bivariate distribution, such as a Gaussian distribution with zero mean, variances ${\sigma }_x^2$ and ${\sigma }_y^2$, and zero covariance. The standard deviations σ_x and σ_y are measures of the single-generation dispersal distance (but see Rousset 2004 for discussion of how this value should be interpreted). If ${\sigma }_x^2={\sigma }_y^2$ this parameterization implies dispersal is isotropic; in these cases, σ² is often defined such that ${\sigma }^2={\sigma }_x^2={\sigma }_y^2$. Finally, to avoid the formation of unrealistic spatial clumps of individuals (Felsenstein, 1975), population density is typically constrained to be uniform across the habitat. One approach to imposing density regulation is to assume each individual occupies a single node on a large lattice. The resulting models are parameterized by σ² and ρ, the density of the population, although in most cases only the joint parameter ρσ² is identifiable.

Various methods for estimating dispersal in CIBD models have been previously proposed, many of which are moment-based. Rousset (1997, 2000) estimate the product ρσ² by regressing pairwise estimates of F-statistics on geographic distance. While this method has been shown to be robust to various violations of the model assumptions (Leblois et al., 2003, 2004), one limitation is that linearity of the regression holds only over a limited, intermediate range of geographic distances that is not known prior to the study. Another moment-based estimator is that of (Neigel et al., 1991), which estimates σ² by assessing the geographic dispersion of mtDNA haplotypes relative to their estimated time of most recent common ancestor (TMRCA). The method has the advantage of being independent of population density of, but it has several drawbacks: it relies on data from only a single non-recombining locus; it fails to account for uncertainty in the estimated TMRCA; and it assumes that a molecular clock holds. Wilkins and Wakeley (2002) provide a coalescent-based, method-of-moments approach applicable to sequence data that uses only average pairwise sequence distances among samples.

More recently, efforts have been made to derive maximum-likelihood estimators of dispersal parameters in CIBD models (Rousset and Leblois, 2007; Meligkotsidou and Fearnhead, 2007). Maximum-likelihood estimators have the advantage of making full use of the data but the potential disadvantage of being difficult to implement. Significant computational challenges exist to implementing likelihood-based methods in population genetics. As a result these methods rely on computational approximations, such as importance sampling, to estimate likelihoods (Stephens and Donnelly, 2000).

Here we propose a novel importance-sampling method for maximum likelihood estimation of dispersal. The proposed method differs from existing likelihood methods in focusing on the geographic distribution of low-frequency alleles only. By restricting the analysis to low-frequency alleles, the computational problem of estimating the likelihood is more tractable than for the full data. The computational gains arise because we need consider only the ancestry of the carriers of the low-frequency allele, rather than the ancestry of the whole sample. Further, the geographic distribution of low-frequency alleles contains most of the information about recent dispersal. Low-frequency alleles are typically descendants of recent mutations and are geographically clustered in the geographic area where the mutation occurred initially. For a given allele frequency, the tightness of this spatial clustering indicates the levels of dispersal. From a coalescent perspective, copies of a low-frequency allele have recent pairwise coalescent times, and previous studies show restricted dispersal has a large effect on the distribution of recent pairwise coalescent times (Wilkins, 2004; Fearnhead, 2007). In addition, by focusing on low-frequency alleles, our method only requires that a population be at demographic equilibrium since the low-frequency alleles in question have arisen. This timescale is much shorter than the time to coalescence of the whole sample (Wiuf, 2000; Slatkin, 2003).

Our method estimates the likelihood of $\rho {\sigma }_x^2$ and $\rho {\sigma }_y^2$ for each locus separately and then combines information from independent loci. It can be applied to datasets with large numbers of independent loci such as single nucleotide polymorphism (SNP) datasets. The likelihood framework provides approximate confidence intervals and allows a likelihood ratio test for equal dispersal in both directions.

Methods

Model

We begin by considering a population genetic sample of L independent bi-allelic loci from a diploid population of size N that is distributed over a finite area of size A with constant density ρ = N/A. Let n = (n₁, . . . , n_L) be the the number of chromosomes sampled at each of the L loci and let j = (j₁, . . . , n_L) be the counts of the derived allele at each of the L loci. Let X_l be a 2×j_l matrix containing elements X_ldk that represent the dth-dimensional geographical coordinate of the kth copy of the derived allele at locus l, and let X = (X₁, . . . ,X_L). Further, we assume that all copies of the derived allele are descendant from a single, unique mutation event (i.e. all copies of the mutation are identical-by-descent). While we focus on bi-allelic loci in our presentation, our method is also to applicable multi-allelic loci (e.g. loci that fit an infinite-alleles model of mutation), as long as each allele considered is at low frequency and identical-by-descent.

For alleles that are identical-by-descent, the history of the ancestral lineages of the allele can be summarized by a single intra-allelic genealogy for each locus which can be decomposed into two portions. First we specify a set of times describing events on the genealogy with time measured in units of N generations from the present day. Let T_l = (T_l1, . . . T_ljl) be a vector of times such that T_l1 is the time at which the first copy of the derived allele arose at locus l and let T_li for i ≥ 2 be the time points in the past at which the number of ancestral lineages in the intra-allelic genealogy decreased from i to i−1 as one looks backwards in time. Let T = (T₁,. . . , T_L). The second portion of the genealogy is the tree topology describing the lineages involved in each of the j_l − 1 coalescent events on the intra-allelic genealogy. Let G = (G₁, . . . ,G_L) be the graphs describing the tree topology of the intra-allelic genealogy at each of the L loci.

To model dispersal, we consider a model with independent dispersal along two perpendicular, geographic axes. We consider the per-generation dispersal distribution along each axis to have a mean of 0 with a variance of ${\sigma }_1^2$ along one axis and a variance of ${\sigma }_2^2$ along the other. We assume the higher moments of the distribution are well-behaved such that after some small duration of time s (measured in units of N generations) the location of a lineage starting at (x, y) is well approximated by a two-dimensional normal distribution with mean (x, y) and a variance-covariance matrix [$[sN{\sigma }_1^2,0],[0,sN{\sigma }_2^2]$]. The precise time-point at which the approximation becomes valid depends on the timescale of coalescent events in the intra-allelic genealogy. In the extreme case where the allele frequency is so rare that intra-allelic coalescent events occur nearly instantaneously, our assumption implies the dispersal distribution must be exactly normal. By assuming that the geographic location of a lineage will be a two-dimensional normal distribution we are implicitly assuming that the positions of each lineage are following a Brownian motion and that boundary effects are negligible. The lack of boundary effects may be reasonable for low-frequency alleles found centrally within large habitats, because such alleles will likely not have dispersed widely enough to have encountered the boundaries of the habitat.

To denote the unobserved geographic position of each of the single mutation events that gave rise to the first copy of each derived allele, let Z_l = (Z_l0, Z_l1) be the coordinates of the location at which the mutation event occurred for locus l and let Z = (Z₁, . . . ,Z_L). Due to the constant density of the population, the location at which a mutation occurs is equally likely across the whole habitat, so that the marginal distribution P(Z_l = z) equals $\frac{1}{A}$ for all z in the habitat.

Furthermore, we make the approximation that the intra-allelic genealogy is independent of the geographical configuration of the lineages. This approximation is also used by Neigel et al. (1991) and Meligkotsidou and Fearnhead (2007) and implicitly assumes weak population density regulation. For our purposes, we note that, even in density-regulated populations, the approximation may be more accurate for low-frequency alleles. In panmictic populations, the number of copies of a low-frequency allele evolves approximately as a linear birth-death process (Slatkin and Rannala, 1997), so that each copy of the allele leaves an independent number of descendant copies in the next generation. The extension that we assume here is that because copies of the low-frequency allele reproduce independently of each other, they will also reproduce independently of each other’s geographic configuration. Given this approximation, the distribution of topologies and coalescent times for the intra-allelic genealogy are described by the birth-death results obtained by Slatkin and Rannala (1997) for randomly mating populations. Specifically, the probability of the vector T_l can be found by considering T_l as j_l ordered samples from the density h(t), where

$$h(t)=\frac{2n_l}{{(2+t{n}_l)}^2}.$$ (1)

This distribution arises from the equations in Slatkin and Rannala (1997) by setting $f=\frac{n_l}{N}$ and measuring time in units of N generations (see Appendix for more detail). The density implies that:

$$P({\mathbf{T}}_l=\{t_1,\dots ,t_{j_l}\})=j_l!{\displaystyle \prod _{i=1}^{j_l}\frac{2n_l}{{(2+t_{li}{n}_l)}^2}.}$$ (2)

for all possible values {t₁, . . . , t_jl}. For the topologies G_l, Slatkin and Rannala’s results provide the following simple distribution which reflects equiprobability of all labelled tree topologies:

$$P(G_l=g)=\frac{1}{{\displaystyle {\prod }_{i=3}^{j_l}\left(\begin{array}{c}{j}_l\\ 2\end{array}\right)}}$$ (3)

for all possible g. To refer to the model, we use the acronym BBM, as our model is a type of branching Brownian motion.

Likelihood-based inference

For performing inference on the model described above, we focus on X, the geographic locations of derived alleles for a set of loci. We are interested in inference on ${\sigma }_1^2$ and ${\sigma }_2^2$ although we can only infer the value of these parameters jointly with ρ; thus the identifiable parameters of the model are $\rho {\sigma }_1^2$ and $\rho {\sigma }_2^2$. We chose to assume the area A was known, and so we instead are only interested in inference on $N{\sigma }_1^2$ and $N{\sigma }_2^2$, knowing that we can convert them to $\rho {\sigma }_1^2$ and $\rho {\sigma }_2^2$ using the known value of A. We define $\theta =(N{\sigma }_1^2,N{\sigma }_2^2)$ and use θ to refer to these parameters succinctly. We are also interested in the special case where $N{\sigma }_1^2=N{\sigma }_2^2$. In this case there is only one identifiable parameter of the model, which we denote as Nσ² or in some cases θ* to be more compact. Finally, there are the unobserved quantities that are crucial components of the probability model. To summarize these “missing data” at each locus we let M_l = (T_l, G_l, Z_l).

Using the notation P_θ(·) for the probability of an event given θ, the likelihood can then be written as:

$$P_{\theta }(\mathbf{X})={\displaystyle \prod _{l=0}^L{P}_{\theta }({\mathbf{X}}_l)}={\displaystyle \prod _{l=0}^L{\displaystyle \int P_{\theta }({\mathbf{X}}_l|{\mathbf{M}}_l)P_{\theta }({\mathbf{M}}_l)d{\mathbf{M}}_l}}$$ (4)

The integration over M_l is intractable analytically for realistic sample sizes because the space of M_l is the set of all possible topologies, all possible vectors of intra-allelic coalescent times, and all possible geographic origins of the derived allele for locus l.

To approximate the integral over M_l, we use a set of approximation techniques. We use a straightforward Monte Carlo approach to integrate over T_l, an importance sampling approach to integrate over G_l, and an approximate analytical integration for Z_l. The details of each approach are described in appendix A.

From the perspective of how well the whole approximation algorithm performs, the critical part of the algorithm is the importance sampling (IS) over G_l. Here we propose an IS distribution, P*(G_l) that proceeds by randomly constructing a tree sequentially backwards in time such that topologies that join geographically proximal lineages are favored. Our distribution P*(G_l) takes two parameters, θ₀ and H. The parameter θ₀ defines a “driving value” of θ, such that the IS distribution will perform best when θ has a value close to θ₀. In practice we use a single set of m simulated values from P*(G_l) to evaluate the approximation to equation P*(X) across a range of values of θ. This allows for significant computational speed-ups because we only need to simulate from P*(G_l) once in order to calculate a series of points on the likelihood surface around θ₀. The parameter H defines the extent to which geographical proximity influences the sampled topologies. H can be thought of as a “heat” parameter in that as its value increases, the entropy of the importance sampling distribution increases. More specifically, a value of H = 1 favors topologies in close proportion to the contribution the topology will make to the calculation of P_θ(X_l|G_l = g_i) while larger values sample topologies more uniformly. The use of H is designed so that as H approaches ∞, the importance sampler P*(G_l) will converge on the straightforward Monte Carlo sampler P(G_l). The roles of the H and θ₀ parameters are described in more detail in the appendix.

Finally, using the approximations to the likelihood, we employ standard optimization routines from the GNU scientific library to maximize the likelihood with respect to θ. We denote the maximum likelihood estimate (MLE) of θ as $\widehat{\theta }=(\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2})$ and the associated likelihood as L(θ̂). We also maximize the likelihood for the constrained model where dispersal is isotropic so that ${\sigma }_1^2={\sigma }_2^2$. The MLE for the constrained case is denoted as $\widehat{{\theta }^{*}}=\widehat{N{\sigma }^2}$ with likelihood $L(\widehat{{\theta }^{*}})$. Given L(θ̂) and $L(\widehat{{\theta }^{*}})$, we can compute the likelihood ratio test statistic λ for the null hypothesis that ${\sigma }_1^2={\sigma }_2^2$ as $\lambda =L(\widehat{{\theta }^{*}})/L(\widehat{\theta })$.

Performance evaluation

To formally evaluate the performance of the likelihood-based inference we take a two-part approach. In both cases we focus mainly on characterizing the sampling distributions of $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2},\widehat{N{\sigma }^2}$, and λ because it is the sampling behavior of these statistics that is most relevant to biological applications.

First, we evaluate the performance of our estimation method on data simulated under the same BBM model that is used to define the likelihood function. This step allows us to assess the performance of the algorithm for numerically approximating the likelihood function and producing estimates of θ. Given that the model underlying the likelihood approach is identical to the model simulating the data, we expect that if the algorithm is performing well we will have a well behaved sampling distribution for the statistics of interest, $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2},\widehat{N{\sigma }^2}$, and λ.

The second step is to evaluate how the method performs on data from forward simulations from a model of individuals distributed on a lattice. The performance of the method on these simulations will be a result of how well the numerical approximation to the likelihood function performs as well as how accurately the BBM model that the likelihood function is based on summarizes the behavior of the lattice-based model.

For the performance evaluations, we fix the value of H to 2, unless stated otherwise. We also fix the value of θ₀ to twice the value of θ used to simulate data, unless stated otherwise. In practice, both the appropriate values of H and θ₀ will depend on the dataset in question (see discussion).

Simulation of the Branching Brownian Motion model

To simulate data under this model, we first fix the number of loci L, the sample sizes per locus n, and the number of derived alleles observed per locus j. We then perform the following steps for each locus l:

1. Draw a topology from the distribution defined by P(G_l) (Equation 3).

2. Draw a vector of times from the distribution defined by P(T_l) (Equation 2). See the “Monte Carlo integration over T_l” section of the appendix for more detail on how to simulate from P(T_l).

3. Assuming the mutation occurs at a geographic location (0, 0), simulate two independent Brownian motions along the intra-allelic genealogy defined by G_l and T_l. The resulting set of geographic locations for the lineages at the present day is stored as a simulated value of X_l.

Simulation of alleles in a finite lattice model

In order to test our method using an alternative model of dispersal in a continuously distributed population, we simulated from a lattice model in which one individual is at each point in a large lattice. Although this model is still highly idealized, it includes density regulation of the individuals, yet it is simple enough that we could generate sufficient sample data with which to test our method. An alternative approach for simulating from a model with density regulation is the coalsecent-based algorithm of Wilkins and Wakeley (Wilkins and Wakeley, 2002; Wilkins, 2004).

We assumed a square lattice of (2l + 1) ×(2l + 1) diploid individuals (where l is an abitrary non-negative integer), and that each generation consisted of two steps, dispersal of an infinitely large migrant pool followed by random sampling of alleles from that migrant pool at each lattice point. In each replicate, the population was initially fixed for allele a. Then at t = 0, one of the copies of a in the individual at the center of the lattice mutated to A to create a heterozygote. Then, each copy of A contributed to the migrant pool at the lattice point d_x and d_y steps away in proportion to a discretized and truncated bivariate normal distribution with mean (0, 0), variances ${\sigma }_x^2$ and ${\sigma }_y^2$, and 0 covariance. We truncated the dispersal distribution for d_x and d_y larger than 3σ_x and 3σ_y in order to speed the computations. We also simulated dispersal according to a modified double-exponential distribution that has been motivated by seed dispersal data (Clark, 1998): $k(d)\propto e^{-{\left|\frac{d}{\propto }\right|}^c}$ where $d=\sqrt{d_x^2+d_y^2}$, α is a scale parameter, and c is a shape parameter. For values of c < 1, the tails of this distribution are not exponentially bounded (i.e. the distribution is “fat-tailed”). For these simulations we truncate the dispersal distribution for x and y larger than 10σ_x and 10σ_y.

The frequency of A at location (x, y), p_x,y, is the sum of the contributions to the migrant pool at that location from all extant copies of A. To create the next generation of adults, we assumed individuals are composed of two alleles independently sampled with the frequency of A allele being p_x,y.

Each replicate continued until A was either lost or fixed. For each set of replicates, we specified a target number of copies, j. Whenever the number of copies of A was exactly j, the locations of those j copies were recorded. At the end of each replicate in which j copies were found at least once, one of the sets of locations was chosen randomly to be the result for that replicate. Replicates were continued until L replicates were obtained in which j copies of A were found at least once. Then the results for that set of replicates were formatted for analysis by our IS program.

Evaluating a single run of the algorithm

A general property of IS algorithms is that their performance can be evaluated by inspecting the distribution of importance sampling weights (Liu, 2002). In particular the variance of the importance sampling weights is useful because in pathological cases, the weights will vary wildly so that the final approximation will be determined by a few large importance sampling weights. A useful summary statistic based on the variance of the importance sample weights is the effective sample size (ESS). Letting g = (g₁, . . . , g_m), the ESS can be defined as:

$$\mathit{\text{ESS}}=\frac{m}{1+{\text{Var}}_{P^{*}(G_l)}(w(g))}$$ (5)

where w(·) is defined in the appendix. The ESS statistic can be interpreted as the effective number of independent samples from the target distribution P_θ(X_l|G_l)P(G_l).

Example application to Arabidopsis thaliana

To provide an example application of the method, we analyzed a dataset representing genetic variation from populations of Arabidopsis thaliana. We use a subset of the data presented in Nordborg et al. (2005). Of the 96 accessions presented byNordborg et al. (2005) we focus on a subset of 49 accessions from Europe (Supplemental Figure 2). The 49 accessions were chosen by first taking the subset of 76 accessions in Europe and then excluding accessions at random that represented multiple samples from a single geographic locale. As a result, the set of 49 accessions represent 49 unique geographic locations across Europe. This last fact is important for application of our method because of the assumption in our model that individuals are sampled randomly from across the habitat and obtaining multiple individuals from the same location is unlikely under random spatial sampling.

We next filter the sequence data to obtain sites that are bi-allelic. We assume minor alleles are derived and limit ourselves to a a fixed low-frequency range [i.e. each has 6 copies of the minor allele segregating (which corresponds to an allele frequency of 6/(2 · 49) ≈ 6%]. The geographic locations of the low-frequency allele at each locus are used to define X. Here we present the results for a simple data set of 8 loci from chromosome 3, chosen to be well-spaced along the chromosome.

Results

Performance of importance sampling approximation

Across a range of exploratory trial values, we found the IS algorithm decreases the Monte Carlo variance relative to using a straightforward Monte Carlo approach. In most cases the IS algorithm outperforms the Monte Carlo sampler by providing estimates of the likelihood surface that are accurate and suffer from little Monte Carlo sampling error (Figure 1); however in some rare cases the IS algorithm produces a likelihood surface that is a clear outlier from the majority of other IS replicates. Typically these aberrant replicates are recognizable by having low values for the ESS statistic and/or importance sampling weights with means that are not approximately 1. These rare replicates likely reflect cases where the importance sampler samples a rare topology with a very large importance sampling weight and so the resulting approximation to the likelihood is dominated by a single replicate. In most cases, increasing the value of H was found to decrease the occurrence of these aberrant runs, although the reduction comes at the cost of increased Monte Carlo variance among the remaining replicates.

Figure 1. Example of the performance of the importance sampling algorithm relative to the straightforward Monte Carlo sampler.

The left panel shows ten replicate estimates of the θ* likelihood surface using 1000 iterations of the importance sampling algorithm. The center panel shows ten replicate estimates using 3000 iterations of the random sampling algorithm. The right panel shows a close approximation to the true likelihood surface (obtained by 10 million replicates of the Monte Carlo sampler). The test case is a simulated sample from 1 locus with 12 minor alleles observed and with θ = (10⁴, 10⁴). For the importance sampling algorithm, H = 1 and θ₀ = (2 × 10⁴, 2 × 10⁴).

Performance on data from the birth-process model

To assess the performance of the importance-sampling-based likelihood method we simulated data under the BBM model that underlies the method. Rather than examine the likelihood surface itself we focus on the properties of the estimators that would be used in an application to data. In particular, we are interested in the performance of the point-estimates $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2},\widehat{N{\sigma }^2}$, their associated confidence intervals, and the likelihood ratio test based on λ. As mentioned above, this step allows us to investigate whether there are any obvious deficiencies in the importance sampling algorithm and to gain insight on the performance of likelihood-based inference for this problem.

We found the sampling variance of the point estimates $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2},\widehat{N{\sigma }^2}$, decreases as either the number of low-frequency alleles observed per locus, j, or the total number of loci, L, increases (Figure 2). For smaller sample sizes the sampling distributions are skewed towards higher values.

Figure 2. Box-plot summaries of the sampling distribution of $\widehat{N{\sigma }^2}$ .

Summaries are plotted across a range for the number of loci and the number of copies of the minor allele observed, and the true value of N σ² is indicated by a horizontal dashed line in each panel. (A) Brownian Birth Process results: Each summary is based on the results of applying the importance sampling algorithm with M = 2000, θ₀ = (200, 200) and H = 2 to 500 datasets obtained by independent simulations from the birth process model with θ = (100, 100). (B) Lattice-model results: Each summary is based on the results of applying the importance sampling algorithm with M = 20000, θ₀ = (102×10⁴, 102×10⁴) and H = 2 to 500 datasets obtained by independent simulations from a 101 × 101 lattice with σ₁ = σ₂ = 5, such that theta = (51 × 10⁴, 51 × 10⁴).

Despite the positive skew in the sampling distribution, the estimators appear to be unbiased. The mean of the estimators is consistently close to the true values used in the simulation, even for values of L and j that represent small sample sizes (j = 3, L = 3). The lack of bias is especially remarkable given the driving value of θ₀ was set to twice the true value of θ used in the simulation. Because $N{\sigma }_1^2,N{\sigma }_2^2$, and Nσ² are scale parameters, proportionally similar results are found when simulations are performed with different values of $N{\sigma }_1^2,N{\sigma }_2^2$, and Nσ² (e.g. the coefficients of variation for each estimator are constant, results not shown).

The sampling distribution of $\widehat{N{\sigma }^2}$ has a lower sampling variance than that of either $\widehat{N{\sigma }_1^2}$ or $\widehat{N{\sigma }_2^2}$, particularly for small sample sizes (Figure 2 vs. Supplemental Figure 3). This result is not unexpected because for $\widehat{N{\sigma }^2}$ the geographic positions of alleles in both dimensions are informative, whereas for $\widehat{N{\sigma }_1^2}$ and $\widehat{N{\sigma }_2^2}$, only the positions of the alleles in a single dimension are informative.

Point estimates of the coverage probabilities for the 2 log-likelihood confidence intervals for $\widehat{N{\sigma }_1^2}$ and $\widehat{N{\sigma }_2^2}$ suggest the confidence intervals are slightly too narrow (e.g. Table 1). Across the conditions we investigated, the average coverage probability is 93.5% for both $\widehat{N{\sigma }_1^2}$ and $\widehat{N{\sigma }_2^2}$. No clear patterns with regards to how the coverage probability changes with the number of loci or number of copies of the low-frequency allele were observed, although asymptotic likelihood theory suggests the coverage probability will approach 95% as the number of loci increases.

Table 1.

Point estimates for the coverage probabilities of the 2 log-likelihood confidence intervals for $N{\sigma }_1^2$.

		No. of copies of allele
Simulation Model	L	3	6	9	12	15
Brownian Birth Process	5	0.920	0.944	0.948	0.942	0.942
	10	0.938	0.946	0.924	0.928	0.934
	15	0.934	0.926	0.938	0.942	0.940
	20	0.932	0.932	0.916	0.930	0.930
Lattice Model	5	0.800	0.836	0.876	0.888	0.924
	10	0.510	0.646	0.756	0.806	0.852
	15	0.356	0.524	0.658	0.732	0.802
	20	0.218	0.460	0.560	0.664	0.756

The coverage probabilities for Nσ² likewise show no clear relationship to L or the number of copies of the low-frequency allele observed at each locus; however one clear difference is that the confidence intervals are closer to the expected value of 95% (Table 2). The average coverage probability across the conditions we investigated was 95.2%.

Table 2.

Point estimates for the coverage probabilities of the 2 log-likelihood confidence intervals for Nσ².

		No. of copies of allele
Simulation Model	L	3	6	9	12	15
Brownian Birth Process	5	0.962	0.954	0.962	0.950	0.938
	10	0.970	0.976	0.960	0.938	0.954
	15	0.956	0.962	0.958	0.962	0.954
	20	0.958	0.952	0.942	0.938	0.914
Lattice Model	5	0.766	0.804	0.864	0.856	0.910
	10	0.432	0.530	0.680	0.706	0.778
	15	0.232	0.370	0.492	0.576	0.698
	20	0.142	0.272	0.424	0.518	0.634

These results show how when we simulate data from the same model underlying our method (the BBM model), we observe reasonable performance. The MLEs have low bias, confidence intervals show approximately the correct coverage, and a likelihood ratio test that is well calibrated with respect to nominal p-values. These results indicate that the importance sampling algorithm for computing the likelihood and subsequent methods for maximizing the likelihood are performing well. However, the BBM model is an approximation to the dynamics of a low-frequency allele that ignores population density regulation. To get a sense of how the method will perform on a model with density regulation, we turn to lattice-based simulations.

Performance on data from the lattice-based model

To assess performance of the method on lattice-based simulations, we again focus on the performance of the point estimates $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2}$, and $\widehat{N{\sigma }^2}$, their associated confidence intervals, and the likelihood ratio test based on λ.

As with data from the BBM model, the sampling variance of the point estimates $\widehat{N{\sigma }_1^2},\widehat{N{\sigma }_2^2}$, and $\widehat{N{\sigma }^2}$ decreases as either the number of loci or the number of low frequency allelels observed per locus, increases. When the number of low-frequency alleles is low we again see a skew towards high values. One important distinction is that for the lattice simulations, we generally observe a modest bias. For example, when we simulate alleles arising on a 101 × 101 lattice with ${\sigma }_1^2={\sigma }_2^2=25$, we find that the estimated values of $\widehat{N{\sigma }_1^2}$, $\widehat{N{\sigma }_2^2}$, and $\widehat{N{\sigma }^2}$ are each biased upwards (Figure 2, Supplemental Figure 2). The bias decreases as the number of copies of the low-frequency allele (j) increases, but it appears to be unaffected by the number of loci (L). One consequence of this bias is that the coverage probabilities of the 95% confidence intervals are poorly behaved - for our simulations, often the lower confidence interval is above the true value of the parameter, resulting in very low coverage of the true value (Tables 1, 2). Coverage increases as j increases, but as L increases the coverage becomes worse. Presumably as L increases one is getting tighter confidence intervals around a central value that is biased, resulting in poorer coverage; whereas when j increases the bias is reduced, hence increasing the coverage probabilities.

To further investigate bias, we conducted experiments to see how habitat size might affect the estimates. Because the BBM does not allow for edge effects, one might expect that as dispersal increases substantially relative to the scale of the habitat, the method might be biased towards underestimating the levels of dispersal. The underestimation would arise because the limited habitat size forces alleles to be more geographically clustered than they would be an infinite habitat, and the excess geographic clustering would appear to the method like reduced dispersal. Our simulations confirm this behavior (Figure 4A). In contrast, when habitat sizes are large relative to the scale of dispersal, we find the estimates are directly proportional to the true underlying values (with a modest bias upwards, Figure 4B).

Figure 4. Lattice model results: Effect of habitat size on bias.

Each panel shows the distribution of MLEs as a function of Nσ². (A) Lattice of size 101 × 101. 100 replicates per value of Nσ². (B) Lattice of size 401 × 401. 25 replicates per value of Nσ². All simulations had L = 10, j = 9.

We considered whether the driving value θ₀ could play a role in the upward bias. In nearly all the previous lattice model simulations the driving value was arbitrarily chosen to be twice the value of $\theta =(N{\sigma }_1^2,N{\sigma }_2^2)$ used to simulate the data (as we did in our simulated data from the BBM model). To assess whether the method is sensitive to this driving value and might bias θ̂ towards θ₀, we studied how the distribution of $\widehat{N{\sigma }^2}$ changes as a function of θ₀ (Supplemental Figure 4). The results show that unless θ₀ is much less than θ (i.e. log₁₀(θ₀ < −1) the results are unaffected by the choice of θ₀. Importantly, even when θ₀ = (and recalling the ideal choice of θ₀ is θ) we find an upward bias. Combined with the observation that the inference for the BBM model was not biased, this suggests the bias is not a result of properties of the importance-sampling approximation for calculating the likelihood.

We next investigated the performance of the likelihood ratio test on the lattice model data (Table 3 and Supplemental Figure 5). We find no clear patterns in how the false positive rate depends on L and j but that overall the false-positive rates are close to the nominal p-value of 0.05 (the average false positive rate across our simulations conditions was 0.044). As in the simulations of the BBM model, the power of the method is proportional to $\text{log}\left(\frac{{\sigma }_1^2}{{\sigma }_2^2}\right)$ and the power increases with j.

Table 3.

Point estimates for the false positive rate of the asymptotic likelihood-ratio test that ${\sigma }_1^2={\sigma }_2^2$

		No. of copies of allele
Simulation Model	L	3	6	9	12	15
Brownian Birth Process	5	0.044	0.054	0.062	0.042	0.056
	10	0.068	0.070	0.060	0.052	0.050
	15	0.072	0.054	0.044	0.060	0.054
	20	0.060	0.046	0.058	0.048	0.040
Lattice Model	5	0.054	0.054	0.056	0.052	0.028
	10	0.058	0.054	0.018	0.036	0.028
	15	0.072	0.046	0.040	0.048	0.038
	20	0.071	0.070	0.038	0.056	0.046

We also considered how the method performs for data generated from an alternative dispersal distribution, with more or less kurtosis than the discretized normal distribution. We used the modified double-exponential distribution, in which the parameter c determines the kurtosis of the distribution. For reference a normal distribution has a kurtosis value of 3, more fat-tailed (leptokurtic) distributions have higher values, and more narrow-tailed (playtkurtic) distributions have lower values. Our results show that as kurtosis increases, the estimates $\widehat{N{\sigma }^2}$ decrease, maintaining an upward bias, until the distribution becomes very leptokurtic (c < 0.75, kurtosis > 12), at which point the estimates have a downward bias (Figure 5).

Figure 5. attice model results: Effect of kurtosis on bias.

The distribution of MLEs is plotted as a function of the kurtosis observed in the modified double-exponential dispersal distribution described in the text. Simulations used c = (0.5, 0.75, 1, 1.5, 2, 4) to produce the 6 different levels of kurtosis, and in each case α was chosen to result in constant standard deviation of 5. Kurtosis was calculated based on the distribution produced after discretization and truncation (see main text). The lattice size was 101 × 101 so that the true underlying value of Nσ² = 51 × 10⁴. 25 replicates per value of c. All simulations had L = 10, j = 9.

Finally, we note that for the lattice model one can convert estimates of Nσ² to estimates of the “neighborhood size”, 4ρπσ² Wright (1943) by dividing $\widehat{N{\sigma }^2}$ by the total area of the population (A) and multiplying by 4π. For example, suppose we obtain the estimate of 6 × 10⁶ for Nσ² on a 200 × 200 lattice. In this case the neighborhood size would be estimated as 1885 individuals.

Application to Arabidopsis thaliana

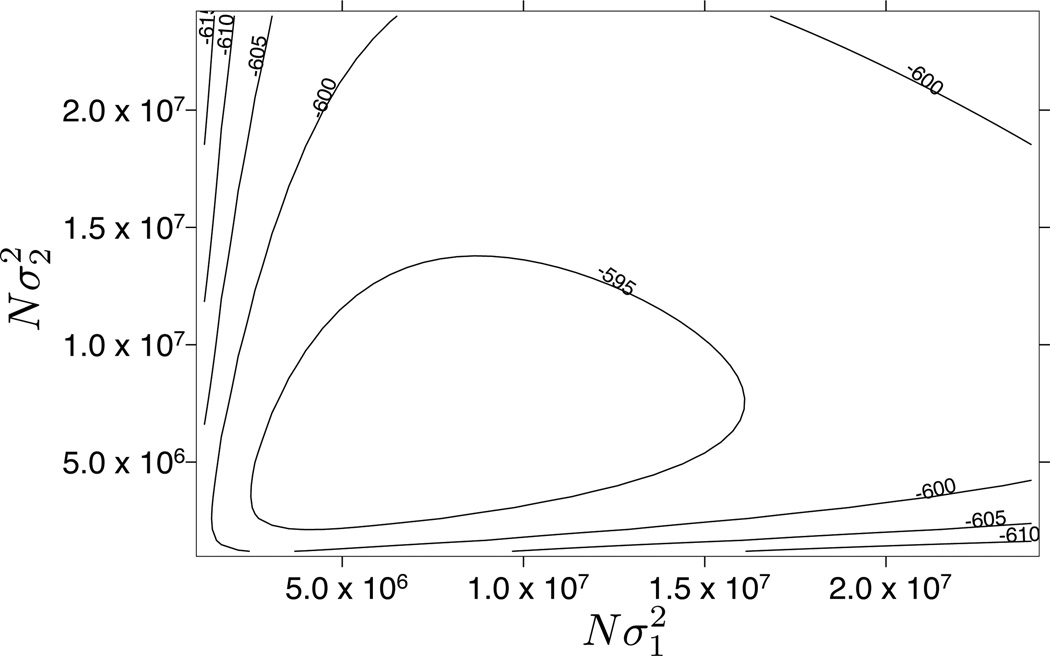
In the sample Arabidopsis dataset, the copies of the minor allele are distributed across a spatial area of hundreds of kilometers in each dimension (Supplemental Figure 6), although the exact extent varies largely from locus to locus. Locus 147 and Locus 7014 have the most compact distributions, while Locus 2123 has the most widespread. The variability from locus to locus in the distribution of the minor allele translates to high variability in the likelihood surfaces for Nσ² at each locus (Figure 6). The curvature of each individual likelihood surface and the variability of the likelihood surface among loci make obvious that precise estimation of Nσ² is difficult using single loci. The joint likelihood curve (Figure 7) has a much more narrow confidence interval ([3.1 × 10⁶, 11.27 × 10⁶]) than any individual locus and an MLE of 5.9×10⁶. Assuming N = 50, 000 the corresponding value of σ would be 10 km. The likelihood surface for $\widehat{N{\sigma }_1^2}$ and $\widehat{N{\sigma }_2^2}$ Figure 8) shows the MLE is close to the line defined by ${\sigma }_1^2={\sigma }_2^2$ and in turn there is no significant support to reject the null hypothesis that ${\sigma }_1^2={\sigma }_2^2$.

Figure 6. The approximate log-likelihood curves for Nσ² for each of the eight loci in the example dataset.

The log-likelihood curves are translated so that the maximum value across the range of 2.5 × 10⁶ km²- 2.5 × 10⁷ km² is positioned at 0 on the y-axis. In some cases the MLE lies outside of this range (e.g., Locus 147 and Locus 7014).

Figure 7. The joint likelihood curve across all loci for Nσ².

The horizontal line intersects the curve at the curve’s maximum value and the two vertical lines demarcate the two log-likelihood support/confidence interval.

Figure 8. The joint likelihood surface across all loci for $N{\sigma }_1^2$ and $N{\sigma }_2^2$.

Discussion

The importance-sampling approach taken here works well for approximating the likelihood of $\widehat{N{\sigma }_1^2}$, $\widehat{N{\sigma }_2^2}$, and Nσ² in the BBM model. Estimates of each parameter are unbiased, confidence intervals for each parameter have roughly the correct coverage probabilities, and the likelihood ratio test of ${\sigma }_1^2={\sigma }_2^2$ has the expected false positive rate. These patterns are true even for small datasets, which is particularly noteworthy since the statistical properties of likelihood estimators are assured only as sample sizes become large. In addition, these patterns were observed across a large number of simulated datasets that were analyzed in batch without any special adjustments to parameters that govern the implementation of the method (H, θ₀, and M). In addition, the computations proceed quickly (for a single locus with 9 copies of the low-frequency allele, 20,000 iterations of the importance sampling algorithm complete in a few seconds on a 3GhZ processor with 16GB RAM). The favorable performance of the inference method under these settings is evidence that the technical challenges of approximating the likelihood function of the BBM and finding its maxima are overcome by the importance-sampling algorithm used here.

Despite the robust performance of the importance-sampling algorithm observed in the BBM simulations, Monte Carlo techniques such as importance sampling should always be used with care. The appropriate settings for H, θ₀, and M will necessarily depend on the dataset in question. Here we found values of H = 2 work well and we found similar results for values of H = 2 − 10 (unpublished results, note: values > 10 not tested). For θ₀, we showed that the choice is not crucial as long as its value is not drastically smaller than the underlying θ for the data-set (Supplemental Figure 5). Because θ is not known a priori a reasonable approach suggested by Supplemental Figure 5 is to run the algorithm iteratively using as θ₀ the θ̂ value from the previous run until the estimate θ̂ does not change. Finally, the larger the value of Mt he better the approximation will be, and it is useful to re-run the algorithm several times. The ESS statistic will indicate whether the estimates are suffering from large Monte Carlo sampling error if the value of M is too small.

To assess the effects of model mis-specification we also simulated data from a lattice model of dispersal. We found our method still performs well, in that the estimated parameters are proportional to their true values, especially for large habitat sizes where boundary effects are minimized (Figure 4). However, we do find a general upward bias - inferred average dispersal distances tend to be larger than the true values. Given the lack of bias for data simulated under the BBM model, we conclude that the bias is due to discrepancies between the dynamics in the lattice and BBM models, and not to the importance-sampling algorithm itself. The bias appears to be caused by the fact that low frequency mutations are dispersing slightly farther than expected given the branch lengths of the intra-alleleic genealogy. Or to restate the same conclusion, given the geographic locations, the branch lengths of the intra-allelic genealogy tend to be somewhat shorter than expected under the linear birth-death model.

The observation of upwardly biased estimates of dispersal in a CIBD model is not unique to our study. Meligkotsidou and Fearnhead (2007) observe a similar bias, and both our methods use the same approximation; namely, the probability distribution for events in the genealogical process occurs independently of the locations of the sampled lineages. This approximation implicitly ignores population density regulation, which is a key feature of the lattice model. Coalescent-based models that explicitly include population density regulation (Wilkins and Wakeley, 2002; Wilkins, 2004; Barton and Depaulis, 2002), are much more challenging computationally, and further work is necessary before they can be adapted for likelihood-based inference. A further consideration is that, in practice, the extent of density regulation may vary across species. For example, Meligkotsidou and Fearnhead (2007) found the performance of their estimator improved in data derived from populations that have been expanding, and we would expect a similar pattern to hold for our estimator.

We also assessed the effects of habitat size and the kurtosis of the dispersal distribution. If the habitat size is small relative to Nθσ², dispersal parameters will be under-estimated. This problem arises because of boundary effects, whereby alleles are being constrained in how far they can disperse, an aspect which is not captured by our model. In practice this suggests that loci with low-frequency alleles that are found near the edges of a habitat should be excluded from datasets prior to applying our approach, or at least analyzed separately with the intention of quantifying boundary effects. We also found that if the dispersal distribution is strongly leptokurtic, dispersal parameters may be under-estimated. This perhaps occurs because the long-range migration events that make a dispersal distribution fat-tailed are unlikely to have been sampled in the time since a low-frequency allele arose by mutation. As a result, low-frequency alleles are more clumped than they would be if dispersal distances were normally distributed. Although the inference algorithm could in principle be based on a different dispersal distribution, that would increase the computational cost because our approach exploits properties of the normal distribution for the peeling algorithm (see Appendix).

Given these considerations, we can tentatively conclude that barring boundary effects and fat-tailed dispersal distributions, our method will often over-estimate the dispersal parameter, and thus it provides an upper bound for the average dispersal distances. There are many complicating factors that we have not addressed, including mis-specification of the derived allele, density-dependent dispersal, directional bias in dispersal, and non-random spatial sampling, that will affect the results from using our method, and its true accuracy cannot be established without detailed modeling of dispersal in a study species. Nevertheless, our method does provide a computationally feasible approach for estimation based on the dispersal of low frequency, relatively young mutations, and those estimates are at least of the right order of magnitude for the models of dispersal considered here.

Figure 3. Power of the asymptotic likelihood-ratio test to detect departures from the null hypothesis that ${\sigma }_1^2={\sigma }_2^2$.

The results are based on inference performed on simulated data from the Brownian birth process model where $N{\sigma }_1^2$ was fixed at 100 and $N{\sigma }_2^2$ was varied across the values 10, 50, 75, 100, 125, 200, 1000. All simulations were fixed at L = 20. Power is estimated from 500 replicate simulations. Similar power curves are found for the lattice model simluations (Supplemental Figure 3).