Tunable patterning of microparticles and cells using standing surface acoustic waves

Abstract

We have developed an acoustic-based tunable patterning technique by which microparticles or cells can be arranged into reconfigurable patterns in microfluidic channels. In our approach, we use pairs of slanted-finger interdigital transducers (SFITs) to generate a tunable standing surface acoustic wave field, which in turn patterns microparticles or cells in one/two-dimensional arrays inside the microfluidic channels—all without the assistance of fluidic flow. By tuning the frequency of the input signal applied to the SFITs, we have shown that the cell pattern can be controlled with the tunability of up to 72%. This acoustic-based tunable patterning technique has the advantages of wide tunability, non-invasiveness, and ease of integration to lab-on-a-chip systems, and shall be valuable in many biological and colloidal studies.

Introduction

The ordered arrangement of biological cells and microscale objects plays an important role in many biological and colloidal studies such as microarrays,^1,2 regenerative medicine,^3,4 and tissue engineering.^5–7 Thus far, many cell/particle patterning techniques have been demonstrated, including optical tweezers,^8,9 magnetic tweezers,^10–12 optoelectronic tweezers,^13–16 hydrodynamic manipulation,^17–23 electrokinetics,^24–29 and bulk acoustic wave-based acoustophoresis.^30–36 Among these approaches, acoustic-based methods^37–62 seem to be ideal for on-chip manipulation or patterning of microparticles/cells, because acoustic methods are inherently non-invasive and can be used to pattern virtually all kinds of microparticles. Recently, we demonstrated an “acoustic tweezers” technique, in which micro-objects were effectively patterned using standing surface acoustic waves (SSAWs) generated by a pair of interdigital transducers (IDTs).⁶³ However, this acoustic tweezers technique shares the same limitation as many other on-chip patterning techniques: features (e.g., the period) of the pattern cannot be modified. Once the device is fabricated, the period of the pattern is established and can be adjusted only within the bandwidth of the IDT (a range of less than 10%).^64,65 In this sense, the previously demonstrated acoustic tweezers technique operates in a static manner.

In this article, we report a major advancement in the acoustic tweezers technique: achieving tunable particle/cell patterning by varying the SSAW field with slanted-finger interdigital transducers (SFITs). Since the period of a SFIT—a variation of the regular IDT—changes continuously from one end to the other, SSAWs at different wavelengths can be generated in between a pair of identical SFITs.^66–69 Thus, control of the frequency of an input AC signal translates into a wavelength- and location-varying SSAW field that in turn patterns microparticles with different features. Such a tunable particle/cell patterning technique is expected to be valuable in many on-chip cell studies^1–6 such as dynamic control of cell-cell interactions.

Working mechanism

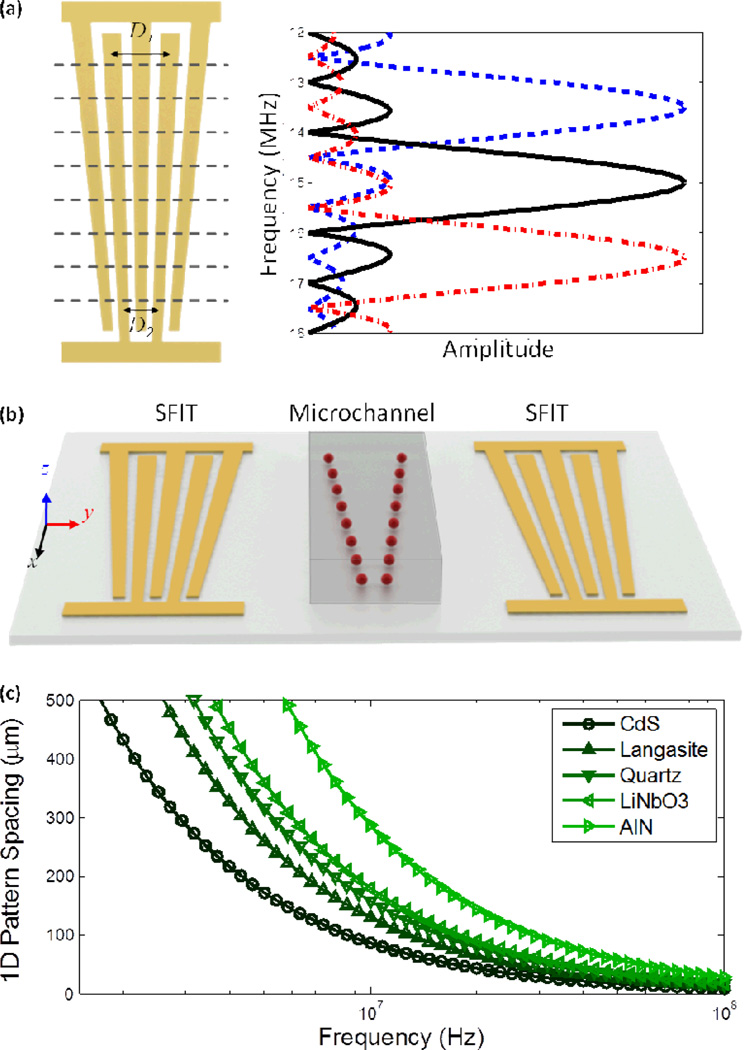
The schematic of a SFIT is shown in the left panel of Fig. 1a. A SFIT can be conceptually considered as a cascade of thin, distinct IDTs with homogenous finger spacing separated by the dotted lines. If the number of sub-channels is large, each sub-channel can be considered a conventional uniform IDT. For each sub-channel, the period of the slanted fingers, D_i, is given by

$$D_i={\lambda }_i=c/f_i,$$ (1)

where λ_i is the wavelength of the SAWs excited by the sub-channel, c is the SAW velocity on the piezoelectric substrate along the propagation direction (normal to SFIT), and f_i is the resonance frequency of the sub-channel.

Fig. 1.

(a) The left panel shows the configuration of a SFIT of which the period is changing continuously. The right panel describes the amplitude distribution of a SAW at different frequencies. (b) A schematic drawing of the acoustic-based, one-dimensional dynamic patterning device. (c) Relationship between frequency and spacing of one-dimensional patterning on different piezoelectric substrates.

When a radio frequency (RF) signal is applied to the SFIT deposited on a piezoelectric substrate, SAWs are generated from the sub-channels where the period of the slanted fingers satisfies eqn (1) to support the resonance condition. Take one of our designs as an example: The period of the SFIT decreases linearly to cover a frequency range of 12 MHz to 18 MHz. When a RF signal is applied at a frequency near the center of the tunable range (15 MHz), the excited SAW has its maximum amplitude at the center of the SFIT with a narrow bandwidth, as shown by the solid black line in Fig. 1a. The bandwidth of the excited SAW is inversely proportional to the number of slanted fingers; the effective aperture A_eff of the excited SAW beam can be approximated as^70,71

$${\mathrm{A}}_{\text{eff}}\cong \frac{1}{\mathrm{n}}\frac{{\mathrm{f}}_0}{{\mathrm{f}}_{\mathrm{h}}-{\mathrm{f}}_1}{\mathrm{A}}_0,$$ (2)

where n is the number of finger pairs, and f₀, f_h, f_l, A₀ are the center frequency, highest frequency, lowest frequency, and aperture length of the SFIT, respectively. If we tune the frequency of the input RF signal, the main SAW beam will be switched to corresponding high-frequency (red dash-dotted line in Fig. 1a) or low-frequency (blue dashed line in Fig. 1a) regions, respectively. Therefore, the SFITs allow dynamic control of the specific position of the maximum SAW amplitude and the acoustic wavelength. It is worth noting that the amplitude of the excited SAW generally varies with frequency when the input voltage is kept constant;⁷² however, it is possible to calibrate the system to obtain a uniform output as shown in the right panel of Fig. 1a. Since the propagation velocity of SAW varies depending on the material properties of the piezoelectric substrate, as shown in Fig. 1c,^73,74 we can also achieve large or narrow pattern spacing for different applications by choosing an appropriate substrate. In this experiment, we use a 128° Y-cut lithium niobate (LiNbO₃) wafer for its optical transparency and high electro-mechanical coupling.

The acoustic-based tunable one-dimensional (1D) patterning devices consist of a polydimethylsiloxane (PDMS) microfluidic channel bonded in between an identical pair of SFITs deposited on a piezoelectric substrate. The pair of SFITs was deposited in a parallel geometry, as shown in Fig. 1b, and an RF signal was split and applied to each SFIT to generate two identical SAWs propagating along the y-axis. These two SAWs propagate in opposite directions and interfere with each other to form a SSAW field in between the SFITs where the PDMS microchannel was bonded (Fig. 1b). Such a SSAW field leads to a periodic distribution of pressure nodes and antinodes on the device substrate. When the resonating SSAW encounters the liquid medium encapsulated in the microchannel, it generates periodic longitudinal pressure waves that cause pressure fluctuations in the medium. The acoustic radiation force, generated from the pressure fluctuations, pushes the suspended particles/cells toward pressure nodes or antinodes in the SSAW field, depending on the elastic properties of microparticles/cells. The primary acoustic radiation force that acts on microparticles can be expressed as⁷⁵

$${\mathrm{F}}_{\mathrm{r}}=-\left(\frac{\mathrm{\pi }{\mathrm{p}}_0^2{\mathrm{V}}_{\mathrm{c}}{\mathrm{\beta }}_{\mathrm{w}}}{2\mathrm{\lambda }}\right)(\mathrm{\beta },\mathrm{\rho })\text{sin}(2\mathrm{k}\mathrm{x}),$$ (3)

$$(\mathrm{\beta },\mathrm{\rho })=\frac{5{\mathrm{\rho }}_{\mathrm{c}}-2{\mathrm{\rho }}_{\mathrm{w}}}{2{\mathrm{\rho }}_{\mathrm{c}}+{\mathrm{\rho }}_{\mathrm{w}}}-\frac{{\mathrm{\beta }}_{\mathrm{c}}}{{\mathrm{\beta }}_{\mathrm{w}}},$$ (4)

where p₀, λ, V_c, ρ_c, ρ_w, β_c, and β_w are the acoustic pressure, wavelength, volume of the particle, density of the particle, density of the medium, compressibility of the particle, and compressibility of the medium, respectively. Eqn (4) describes the acoustic contrast factor, ϕ, which determines whether the particles move to pressure nodes or antinodes; the particles will aggregate at pressure nodes when ϕ is positive and pressure antinodes when ϕis negative. To the best of our knowledge, most particles and cells have positive ϕ, and go to pressure nodes in the SSAW fields; bubbles and lipids usually have negative ϕ and move to pressure antinodes.³⁶ Since the acoustic radiation force is directly acting on the particles/cells, our tunable pattern is achieved without the assistance of fluidic flow. In a 1D SSAW field, the pressure nodes (or antinodes) are arranged in multiple lines, resulting in a 1D dynamic patterning of particles along these lines, as shown in Fig. 1b. The period of the 1D pattern depends upon the frequency applied to the SFITs.

Methods

Design principle

Here we describe a general design rule for SAW-based 1D patterning. To obtain a tunable SAW frequency ranging from f₁ to f₂ on a piezoelectric wafer with a SAW velocity c, the period of each SFIT was designed to vary linearly from c/f₁ (D₁ in Fig. 1a) to c/f₂ (D₂ in Fig. 1a) per eqn (1). The width of each electrode is normally kept one quarter of the period. Two SFITs and a PDMS microchannel are aligned parallel to each other. The period of the particle pattern is equal to the period of the resultant SSAW field, which is half of the working wavelength of SAW. As a result, the period of the tunable particle pattern ranges linearly from c/2f₁ to c/2f₂.

Device fabrication

To fabricate these acoustic-based tunable particle-patterning devices, a double layer of chrome and gold (Cr/Au, 50 Å /800 Å) was deposited on a photoresist-patterned 128° Y-cut LiNbO₃ wafer, followed by a lift-off technique to form the SFITs. A single-layer PDMS channel was fabricated with standard soft-lithography and mold replica techniques, and was then aligned and bonded on the LiNbO₃ substrate in between SFITS to obtain the desired devices.

System setup

The experiments were conducted on the stage of an inverted microscope (Nikon TE2000U). Solutions of fluorescent polystyrene (Dragon Green) beads with diameter of 4.16 µm and 7.32 µm were injected into the microfluidic channel by a syringe pump (KDS210 Kd Scientific) before the RF signal was applied. A signal generated by a RF signal function generator (Agilent E4422B) was split into coherent signals after being amplified with a power amplifier (Amplifier Research 100A250A). These coherent signals were then applied to the SFITs to generate SAWs at the designated frequency. A CCD camera (CoolSNAP HQ2, Photometrics, Tucson, AZ) was connected to the microscope to record the patterning process. The applied RF power on devices was 26 dBm in patterning micro polystyrene beads and 23 dBm in patterning bovine red blood cells.

Tunable 1D patterning

Dynamic patterning of micro polystyrene beads

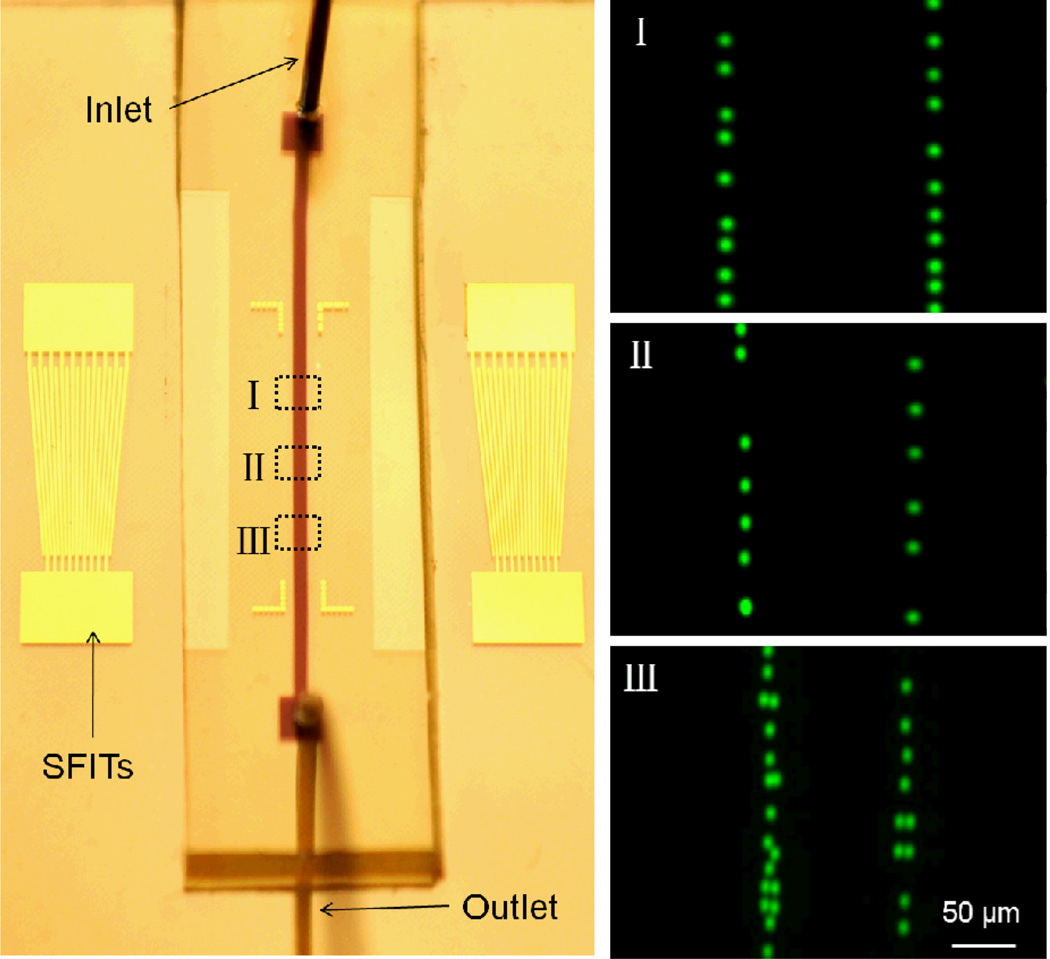
The optical image of a tunable particle-patterning device is shown in the left panel of Fig. 2. The aperture and number of fingers of the SFITs are 5 mm and 10 pairs, respectively. The width of the SFIT fingers varies linearly from 50 µm to 75 µm along the aperture, corresponding to a SAW wavelength range from 200 µm to 300 µm. The width of the PDMS microchannel is 200 µm. Inside the channel, the pattern period equals half the wavelength, which corresponds to the pressure-node separation. The propagation direction of the SFIT-generated SAW was set along the crystal x-axis of the 128° rotated, Y-cut single crystal LiNbO₃ substrate, and thus the generated SAW frequency range was 12 MHz to 18 MHz. Here, we demonstrate tunable patterning using fluorescent (Dragon Green) polystyrene beads with a mean diameter of 7.32 µm suspended in water. The acoustic contrast factor ϕ of the beads is positive, causing them to aggregate at the pressure nodes upon SSAW generation. The microscope-captured images are displayed in the right panel of Fig. 2. When a RF signal was input into the SFITs at 12 MHz, polystyrene beads were patterned in two lines with a period of ~150 µm (Fig. 2-I) in the area where the period of the slanted fingers satisfies the resonance condition defined by eqn (1). Beads located outside of this area were not patterned. When the input RF signal was tuned to 15 MHz, the actively patterned area moved to the center of the device, with a corresponding period of ~120 µm (Fig. 2-II). When the RF signal was further increased to 18 MHz, the patterned area appeared only at the downstream end of the device with a period of ~100 µm (Fig. 2-III). By design, the measured results match well with the period of the SSAWs. Thus, we have shown that our device can dynamically pattern microparticles in 1D arrays with periods ranging from 100 µm to 150 µm. Note that due to the low diffusion rate of the microparticles, we can program the function generator to scan the RF signal frequency over the whole working range of the device to form a continuous pattern in the microfluidic channel, as illustrated in Fig. 1b. In our previous work,⁶³ we have shown the stationary pattern, with which we can achieve only one specific pattern in one single device. In this work, we improved this stationary pattern into a dynamically tunable pattern, in which different particle’s/cell’s patterns can be dynamically achieved in a single device. This flexibility of particle patterning could be helpful in many fundamental research and biomedicine studies. The ability to precisely control the physical distance between two particles/cells facilitates the investigation of cell behaviors such as cell-to-cell interactions and chemotaxis studies. For example, controlling the physical position of two cytochalasin D microsources would help study the migration behaviors of human neutrophil HL-60 cells.⁷⁶ Such tunable patterns can also be useful in tissue engineering. For example, we can first fill the channel with stromal cells, pattern and culture them on the substrate, and then refill with hepatocyte cells, and pattern them in a different array. By tuning the pattern, we can control the distance between these two types of cells, and thus facilitate investigation of their interactions.⁷⁷

Fig. 2.

1D dynamic patterning of fluorescent polystyrene beads. Left: the optical images of the 1D tunable patterning device. The microchannel covers two lines of the pressure nodes of the SSAW. Right: I, II, and III show the 1D pattern at the frequencies of 12 MHz, 15 MHz, and 18 MHz, respectively. The period in region I, II, and III is 150 µm, 120 µm, and 100 µm, respectively.

Quantitative force analysis

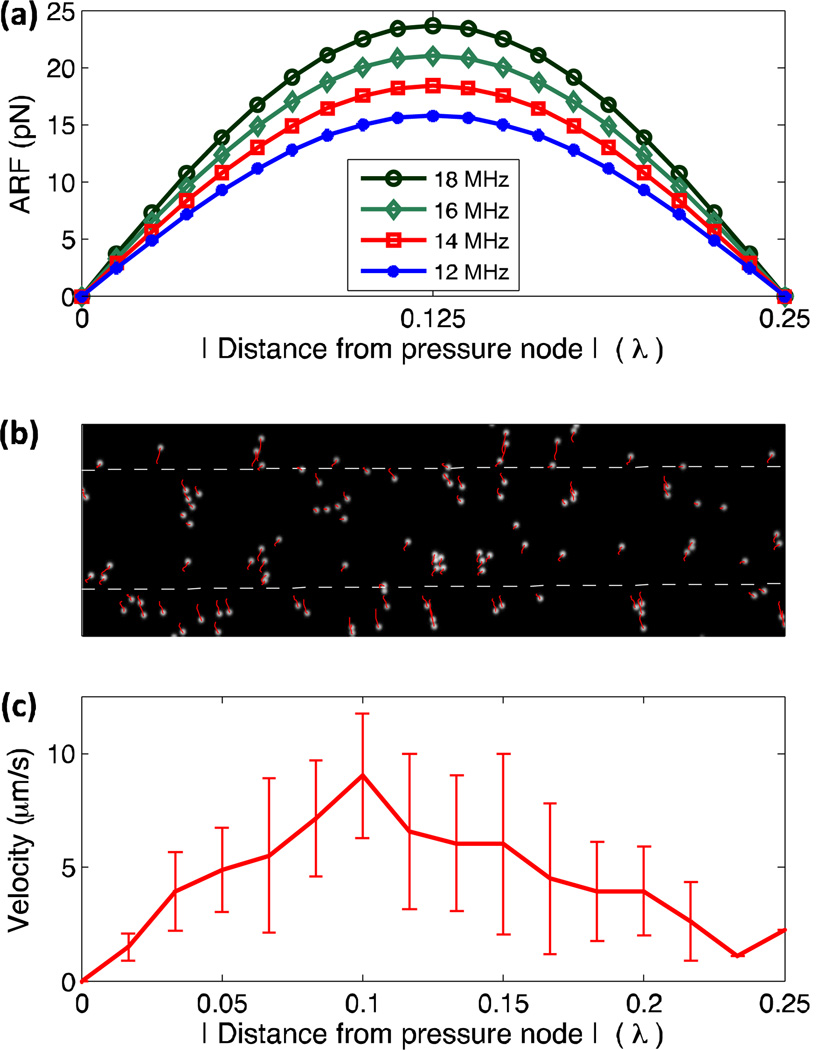
Particles in a microfluidic channel under the influence of a SSAW field are subjected to four forces: the primary radiation acoustic force, viscous drag force, gravity force, and buoyant force. Among these forces, the buoyant force and gravity force act along the channel height direction and typically balance one another due to their similar magnitudes and opposite directions. The viscous drag force is a passive force which is proportional to the particle velocity and acts along the direction opposite to the particle migration. As a result, particle patterning can be analyzed by examining the primary acoustic radiation force, which is given in eqn (3). Fig. 3a shows the calculated distribution of the primary acoustic radiation force within a quarter wavelength range under different frequencies. The primary acoustic radiation force varies with distance from the pressure node in the form of a sinusoid function. The maximum force is located between a pressure node and a pressure antinode (0.25 λ), with its value proportional to the operating frequency. When a SSAW field is generated across the microfluidic channel, the primary acoustic radiation force pushes the suspended particles toward the closest pressure nodes. The induced viscous drag force then counters the acoustic radiation force; therefore, examining particle velocity reveals information about the acoustic radiation force acting on the particles. We recorded the movement of the particles in a 1D SSAW field at the frequency of 12 MHz in Fig. 3b. The white dots in Fig. 3b are the particles before SAWs were generated, and the red lines are the trajectories of particles over the recorded time span. The applied RF power on devices was 26 dBm and the patterning time was around 10 s. The dependence of the particle velocity on the distance from the pressure node is given in Fig. 3c. The velocity distribution shows a maximum between the pressure node (x=0) and the pressure antinode (x=0.25λ), which agrees well with the theoretical analysis of the acoustic radiation force (Fig. 3a).

Fig. 3.

(a) The distribution of primary acoustic radiation force with dependence of frequency. (b) The motion tracking of particles in a SSAW field. (c) Distance dependence of particles’ velocity.

Dynamic patterning of human promyelocytic leukemia cells

To verify the applications of our tunable patterning technique to biological cells, we performed patterning of HL-60 Human promyelocytic leukemia cells. When the SFITs were excited with a frequency of 31 MHz, cells were patterned with a period of 60 µm in the region corresponding to a small finger pitch (as shown in Fig. 4-I). The RF power was 23 dBm and the patterning time was less than 10 s. When the frequency was tuned to 25 MHz and 13 MHz, cells were patterned in the regions corresponding to median and large finger pitch with a period of ~78 µm (Fig. 4-II) and ~150 µm (Fig. 4-III), respectively. The tunable bandwidth of the spatial period (150 µm – 60 µm = 90 µm) is 72% (90/125=72%) of the period at the center of the tunable range ((150 µm + 60 µm)/2=125 µm). Eqn (3) shows that the acoustic force is depending on the frequency and elastic properties. In this work, the acoustic force is larger on polystyrene beads than on cells; this is one of the reasons why the cell’s pattern is not as well confined as the bead’s pattern. The difference of the acoustic force exerting on cells and particles also results in a longer pattern time for cells than for particles. We note here that the pattern time at high frequency (as shown in Fig. 4-I) is less than that at low frequency (Fig. 4-III). This is because the acoustic force is larger at high frequency than that at low frequency.

Fig. 4.

Dynamic patterning of bovine red blood cells. I, II, and III show the 1D pattern at the frequencies of 45 MHz, 36 MHz, and 27 MHz, respectively.

Tunable 2D patterning

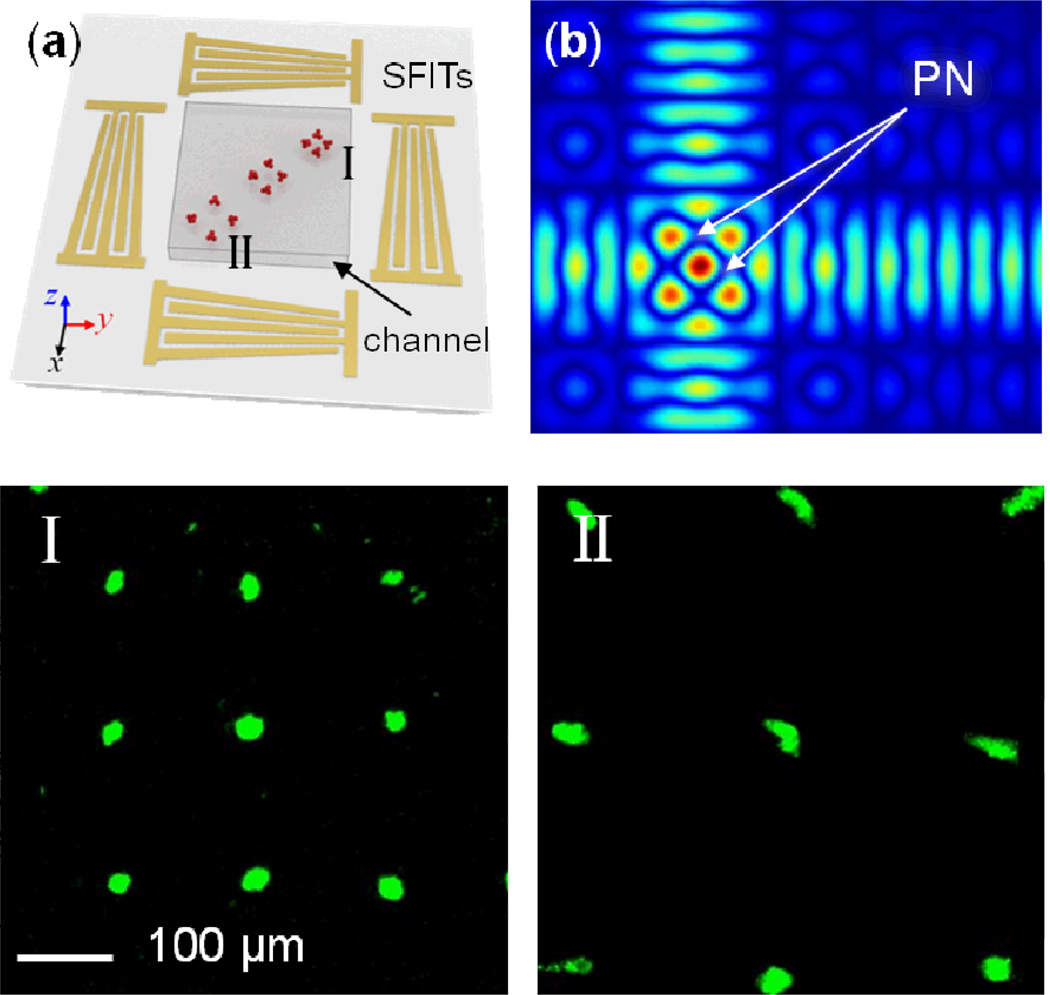
Our acoustic-based particle-patterning technique can be extended to obtain tunable 2D patterning. Fig. 5a shows the schematic of the 2D tunable patterning device, where two identical pairs of SFITs are arranged orthogonally. When a RF signal is applied to all SFITs, two SAWs were generated at the corresponding frequency regions from all four SFITs and interfere with each other to form a 2D SSAW field. The simulated 2D SSAW field is portrayed in Fig. 5b, where we see pressure nodes (PN) formed in orthogonal 2D arrays that are tilted at an angle of 45° with respect to the x-axis. The pattern of pressure nodes, and thus the patterned particles in the region corresponding to a smaller finger pitch (higher frequency) have a smaller period, while the pattern in the region corresponding to a larger finger pitch (lower frequency) has a larger period. The period of the 2D-patterned array is   times the SAW wavelength. As a result, we can control the period of the 2D pattern simply by adjusting the frequency of the input RF signal.

Fig. 5.

2D dynamic patterning of fluorescent polystyrene microbeads. (a) Schematic of the 2D dynamic patterning device: the particle pattern in the region corresponding to a smaller finger pitch (higher frequency) has a smaller period, while the pattern in the region corresponding to a larger finger pitch (lower frequency) has a larger period. (b) The simulated distribution of pressure nodes (PN) in a SSAW field with the SAW excited from the low frequency region of the SFITs. (c) An optical image of the 2D patterning device. Bottom figures I, II and III show the patterned arrays with periods of 150 µm, 195 µm, and 240 µm at the frequencies of 18.0 MHz, 13.3 MHz, and 10.9 MHz, respectively.

The 2D dynamic patterning device consists of two identical pairs of SFITs deposited on a LiNbO₃ substrate in an orthogonal arrangement. The aperture of the SFITs is 2.5 mm— the same length as the square microfluidic channel. The period of the SFIT fingers varies linearly from 200 µm to 350 µm, corresponding to a range of SAW frequencies from 10.5 MHz to 18.5 MHz. Therefore, in theory, the period of the generated 2D SSAW field and the 2D particle-pattern can be tuned from 141 to 250 µm. We used fluorescent polystyrene beads of 4.16 µm diameter to examine the 2D dynamic patterning effect. The two images at the bottom of Fig. 5 illustrate the 2D particle-patterning results at different frequencies. When the SFITs were excited with RF signals at 18 MHz, polystyrene beads in the upper corner of the channel were driven to the 2D pressure nodes, as shown in Fig. 5-I. The measured period of the array was 150 µm, which is close to the theoretical prediction of 145 µm. When the frequency was tuned to 10.9 MHz, particles were patterned in the lower corner (Fig. 5-II) of the microfluidic channel. The measured periods of the patterned arrays are 240 µm; this is in excellent agreement with the theoretical prediction of 240 µm. Thus, we have demonstrated dynamic control of the period of a 2D pattern in the range from 150 µm to 240 µm, by tuning the RF signal frequency. The tunable bandwidth of the spatial period (240 µm − 150 µm = 90 µm) is 46% of the period at the center of the tunable range ((240 µm + 190 µm)/2=195 µm). This range can be further extended by increasing the gradient of the SFITs, so as to correspond with a wider range of working frequencies. However, one must consider that SAWs can be simultaneously excited at the fundamental and harmonic frequencies in large gradient SFITs to result in multiple patterning areas.

It is worth noting that the size of the bead aggregations at the pressure nodes expanded with decreasing frequency. This phenomenon is caused by two major factors. First, based on the assumption that the initial bead distribution was uniform in the solution, the period of the array at a higher frequency (shorter wavelength) is smaller than that of the array at a lower frequency. Thus, fewer beads are collected at each pressure node at higher frequencies, resulting in smaller-size aggregations. Second, from eqn (3) we learned that smaller wavelengths (higher frequency) lead to larger acoustic radiation forces on particles, resulting in more compact aggregation.

Conclusions

In conclusion, we have developed an effective tunable patterning technique using slanted finger interdigital transducers by which the wavelength and position of the excited surface acoustic waves can be dynamically adjusted. Different patterns of microscale particles and cells in different regions can be dynamically achieved simply by controlling the frequency of the input signal without moving any on-chip or off-chip parts. Tunable periods with a range of 100 µm to 150 µm for 1D patterning and 150 µm to 240 µm for 2D patterning have been realized without the assistance of fluidic flow. This acoustic-based tunable particle/cell patterning technique is inherently non-invasive, increasing the potential for application in microarrays, cell studies, and tissue engineering.