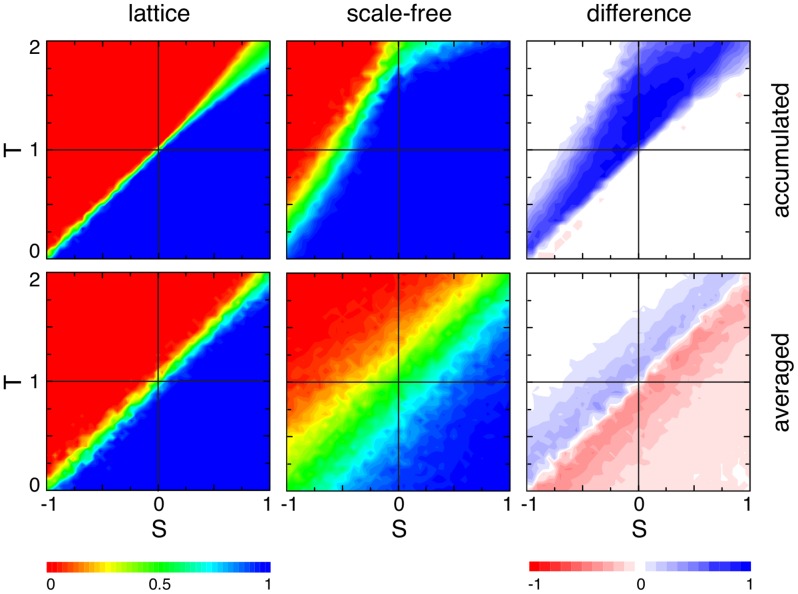
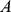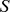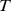Figure 3. Average fraction of strategy for accumulated (top row) versus averaged (bottom row) payoffs in homogenous (left column) and heterogeneous (middle column) populations as well as the difference between them (right column) as a function of the game parameters and (see Table 1).

In each panel the four quadrants indicate the four basic types of generalized social dilemmas: prisoner's dilemma (upper left), snowdrift or co-existence games (upper right), stag hunt or coordination games (lower left) and harmony games (lower right). Homogenous populations are represented by 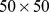lattices with von Neumann neighbourhood (degree 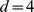) and heterogenous populations are represented by Barabási-Albert scale-free networks (size 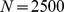, average degree 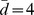). The population is updated according to the imitation rule Eq. (9). The colours indicate the equilibrium fraction of strategy 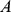(left and middle columns) ranging from 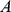dominates (blue), equal proportions (green), to 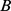dominates (red). Increases in equilibrium fractions due to heterogeneity are shown in blue shades (right column) and decreases in shades of red. The intensity of the colour indicates the strength of the effect. Accumulated payoffs in heterogenous populations shift the equilibrium in support of the more efficient strategy 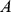except for harmony games where 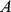dominates in any case (bottom right quadrant). Conversely, for averaged payoffs the support of strategy 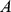is much weaker and even detrimental for 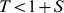. Parameters: initial configuration is a random distribution of equal proportions of strategies 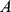and 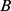; each simulation run follows 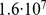updates and the equilibrium frequency of 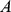is averaged over the last 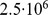updates; results are averaged over 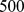independent runs; for scale-free networks the network is regenerated every 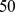runs. No mutations occured during the simulation run.