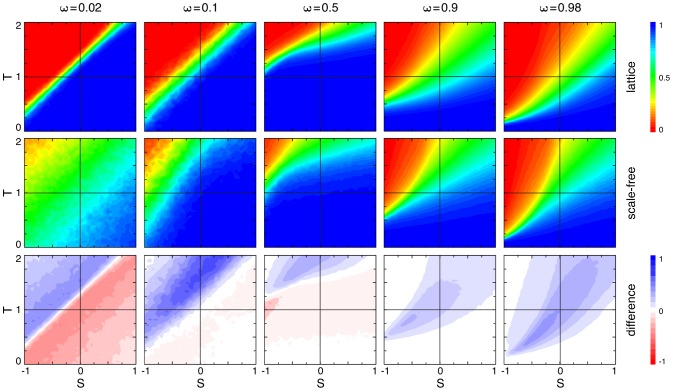
Figure 6. Average fraction of strategy 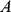for different ratios between interactions and strategy updates in homogenous (top row) and heterogeneous (middle row) populations and the difference between them (bottom row) as a function of the game parameters and (c.f. Figure 3).

Interactions occur with probability 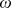and strategy updates with 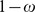. For example, for 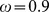each individual has, on average, initiated 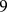interactions between strategy updates but only an average of 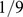interactions for 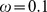. For small 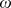effects of heterogenous population structures have little chance to manifest themselves and the results are closer to those for averaged payoffs (c.f. Figure 3). In contrast, for large 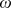heterogeneity plays an important role: for scale-free networks it is guided by the structural heterogeneity whereas in homogenous populations another form of heterogeneity spontaneously emerges in the number of interactions. Even on lattices, stochastic differences in the number of interactions get amplified by the dynamics because an increased number of interactions reduces the chances that an individual updates its strategy (c.f. Figure 7). As a consequence the results for lattices and scale-free networks become increasingly similar but scale-free networks keep promoting 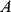types to a greater extend. Parameters and averaging technique are as in the caption to Figure 3.