Noise-weighted spatial domain FBP algorithm

Abstract

Purpose: The purpose of this paper is to implement a noise-weighted filtered backprojection (FBP) algorithm in the form of “convolution” backprojection, but this “convolution” has a spatially variant integration kernel.

Methods: Noise-weighted FBP algorithms have been developed in recent years, with filtering being performed in the Fourier domain. The noise weighting makes the ramp filter in the FBP algorithm shift-varying. It is not efficient to implement shift-varying filtration in the Fourier domain. It is known that Fourier-domain multiplication is equivalent to spatial-domain convolution. An expansion method is suggested in this paper to obtain a closed-form integration kernel.

Results: The noise weighted FBP algorithm can now be implemented in the spatial domain efficiently. The total computation cost is less than that of the Fourier domain implementation.

Conclusions: Computer simulations are used to show the three-term expansion method to approximate the filter kernel. A clinical study is used to verify the feasibility of the proposed algorithm.

INTRODUCTION

The filtered backprojection (FBP) algorithm has been in use for several decades.^{1, 2, 3, 4, 5} It is the workhorse of x-ray CT image reconstruction. A drawback of the FBP algorithm is that it may produce very noisy images. Algorithms based on optimization of an objective function are able to incorporate the projection noise model and produce less noisy images than the FBP algorithm. Usually these algorithms are iterative algorithms.^{6, 7, 8, 9, 10} In order to shorten the computation time of an iterative algorithm, effort has been made to transform a regular iterative algorithm into an iterative FBP algorithm.¹¹ Another approach to noise control is to apply an adaptive filter or nonlinear filter to the projection measurements.^{12, 13} We recently developed a noniterative FBP algorithm that can model the projection noise on a view-by-view or ray-by-ray basis.^{14, 15}

One drawback of the noise-weighted FBP algorithm presented in Ref. 15 is that the modified ramp filtering must be implemented in the Fourier domain, because we did not know the expression of the spatial-domain “convolution” kernel. It is not efficient to implement shift-varying filtration in the Fourier domain. Projection data at each view must be filtered multiple times (say, 11 times) if the Fourier domain filtering method is used as suggested in Ref. 15.

It is known that Fourier-domain multiplication is equivalent to spatial-domain convolution. In principle, any FBP algorithm with Fourier-domain filtering can find its equivalent FBP algorithm that performs filtering in the spatial domain as convolution, if the convolution kernel can be readily obtained.

This paper will implement the noise-weighted FBP algorithm presented in Ref. 15 in the form of “convolution” backprojection. However, this “convolution” is not a true convolution operation, because the integration kernel varies according to the noise variance. An expansion method will be suggested in this paper to obtain a closed-form integration kernel so that the “convolution” can be computed efficiently.

METHODS

Section 2A will review and summarize what we already know about the noise-weighted FBP algorithm, according to our recent publications.^{14, 15, 16, 17, 18, 19, 20} Section 2B is the main contribution of this paper, and the Fourier-domain filtering in the noise-weighted FBP algorithm will be converted into spatial-domain filtering in the form of a dot product, which is similar to convolution.

Noise-weighted FBP algorithm

The noise-weighted FBP algorithm was derived based on minimizing the following weighted least-squares objective function v( f ) with a data fidelity term and a Bayesian penalty term:

$$\begin{array}{ccc}\hfill v\left(f\right)& =& {‖\left[Rf\right](s,\theta )-p(s,\theta )‖}_w^2\hfill \\ & & +\beta {‖f(x,y)**c(x,y)-g(x,y)‖}^2,\hfill \end{array}$$ (1)

where the image to be reconstructed is f(x, y) and its Radon transform is [Rf](s, θ), which is defined as⁵

$$\begin{array}{c}\hfill \left[Rf\right](s,\theta )=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}f(x,y)\delta (x\cos \theta +y\sin \theta -s)dxdy.\end{array}$$ (2)

In Eq. 2, δ is the Dirac delta function, θ is the detector rotation angle, and s is the line-integral location on the detector. The Radon transform [Rf](s, θ) is the line-integral of the object f(x, y). Image reconstruction is to solve for the object f(x, y) from its Radon transform [Rf](s, θ). The first term in Eq. 1 is the data fidelity term that encourages the Radon transform of f(x, y) to be close to the measured projections p(s, θ). In the first term, the norm is the conventional L² norm with a weighting function w. The second term in Eq. 1 is the Bayesian term that encourages a filtered version of f(x, y) to look like a prior image g(x, y), and the parameter β controls the relative importance with respect to the first term.

The function c(x,y) is a symmetric image domain convolution kernel and “**” represents the image domain 2D convolution. If c(x,y) is the 2D Dirac delta function δ(x, y) = δ(x) · δ(y), then the Bayesian term encourages f(x, y) to be similar to g(x, y). For example, f(x, y) can be a high-noise dynamic image and g(x, y) can be a low-noise slow-motion image by averaging images from adjacent time frames.

If g(x, y) = 0 and c(x, y) = δ(x, y), the Bayesian regularization term encourages a minimum norm solution. [Note: There was a mistake in the Appendix A of Ref. 19 where we said that when c(x, y) = 1 the regularization term encourages a minimum norm solution.] If g(x, y) = 0 and c(x, y) is a Laplacian kernel (i.e., the sum of second-order partial-derivative kernels), the regularization term encourages a smooth image.

After minimizing the objective function 1 by using the calculus of variations,²¹ the optimal solution f(x, y) must satisfy an Euler-Lagrange equation,¹⁹ which is an integral equation and may not have an explicit solution if the weighting function w depends on both variables s and θ. If we restrict that the weighting function w only depends on θ with tan θ = ω_y/ω_x, not on s, an explicit solution of the optimal solution f(x, y) can be obtained in the Fourier domain:

$$\begin{array}{ccc}\hfill F({\omega }_x,{\omega }_y)& =& \frac{w\left(\theta \right)·B({\omega }_x,{\omega }_y)+\beta ·G({\omega }_x,{\omega }_y)·C(-{\omega }_x,-{\omega }_y)}{\frac{w\left(\theta \right)}{\sqrt{{\omega }_x^2+{\omega }_y^2}}+\beta ·{\left|C({\omega }_x,{\omega }_y)\right|}^2}\hfill \\ & =& \frac{\sqrt{{\omega }_x^2+{\omega }_y^2}·B({\omega }_x,{\omega }_y)+\beta ·\frac{C(-{\omega }_x,-{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}}{w\left(\theta \right)}·G({\omega }_x,{\omega }_y)}{1+\beta ·\frac{\sqrt{{\omega }_x^2+{\omega }_y^2}·{\left|C({\omega }_x,{\omega }_y)\right|}^2}{w\left(\theta \right)}},\hfill \end{array}$$ (3)

where B, C, F, and G are the 2D Fourier transform of b, c, f, and g, respectively. The derivation of Eq. 3 was given in Refs. ¹⁸ and ¹⁹. It is interesting to see two extreme cases of Eq. 3. In the case of β = 0, Eq. 3 becomes

$$w\left(\theta \right)F({\omega }_x,{\omega }_y)=w\left(\theta \right)·B({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}$$

or (assuming w(θ) ≠ 0)

$$F({\omega }_x,{\omega }_y)=B({\omega }_x,{\omega }_y)\sqrt{{\omega }_x^2+{\omega }_y^2}.$$ (3a)

In the case of β = ∞, Eq. 3 becomes

$$F({\omega }_x,{\omega }_y){\left|C({\omega }_x,{\omega }_y)\right|}^2=G({\omega }_x,{\omega }_y)·C(-{\omega }_x,-{\omega }_y)$$

or

$$F({\omega }_x,{\omega }_y)·C({\omega }_x,{\omega }_y)=G({\omega }_x,{\omega }_y).$$ (3b)

Equation 3a enforces the data fidelity term in the objective function 1 and Eq. 3b enforces the Bayesian penalty term in Eq. 1. Here b(x, y) is the pure backprojection of the raw projections without any filtering. Using the Central Slice Theorem,⁵ an FBP algorithm can be readily obtained from Eq. 3 as

$$f(x,y)=\underset{0}{\overset{\pi }{\int }}{\left.q(s,\theta )\right|}_{s=x\cos \theta +y\sin \theta }d\theta ,$$ (4)

where q is the filtered version of the combined data p_combined:

$$p_{\mathrm{combined}}(s,\theta )=p(s,\theta )+\frac{\beta }{w\left(\theta \right)}·p_g(s,\theta )$$ (5)

and the convolution kernel h_w(θ)(s) for the filter is a modified ramp filter kernel and is defined as

$$\begin{array}{ccc}\hfill h_{w\left(\theta \right)}\left(s\right)& =& 1\mathrm{D}\mathrm{Inverse}\mathrm{Fourier}\mathrm{Transform}\hfill \\ & & \times \left\{\frac{\left|\omega \right|}{1+\beta ·\frac{\left|\omega \right|·{\left|C_1\left(\omega \right)\right|}^2}{w\left(\theta \right)}}\right\}.\hfill \end{array}$$ (6)

Thus, the function q used in Eq. 4 is the convolution of p_combined and h_w(θ)(s) with respect to variable s:

$$q(s,\theta )=p_{\mathrm{combined}}(s,\theta )*h_{w\left(\theta \right)}\left(s\right).$$ (7)

It is interesting to notice that when β = 0, the filter defined in Eq. 6 is reduced to the conventional ramp filter and the noise weighting is not effective. Therefore, it is important to include a Bayesian term in the objective function if you intend to enforce noise weighting in an FBP reconstruction.

In Eq. 6, C₁(ω) is a central section of C(ω_x, ω_y). If c(x, y) = δ(x, y), then C₁(ω) = 1. In Eq. 5, the secondary data p_g(s, θ) are generated from the prior image g(x, y) by first convolving with the filter kernel c(x, y), second performing forward projection, and third ramp filtering. In order to understand the reason that a ramp filtering procedure is needed in generation of p_g(s, θ), we notice that b(x, y) is the backprojection of p(s, θ); g(x, y) is the backprojection of p_g(s, θ) [at this moment, let us temporally assume c(x, y) = δ(x, y)]; b(x, y) is a blurred image; g(x, y) is a sharp image as f(x, y).

In the rest of the paper except Sec. 2E, we will only consider the case of c(x, y) = δ(x, y) and g(x, y) = 0 for the sake of simplicity. In this special case, we have

$$\begin{array}{ccc}\hfill h_{w\left(\theta \right)}\left(s\right)& =& 1\mathrm{D}\mathrm{Inverse}\mathrm{Fourier}\mathrm{Transform}\hfill \\ & & \mathrm{of}\left\{\frac{\left|\omega \right|}{1+\frac{\left|\beta \right|}{w\left(\theta \right)}·\left|\omega \right|}\right\},\hfill \end{array}$$ (8)

and

$$f(x,y)=\underset{0}{\overset{\pi }{\int }}{\left.[p(s,\theta )*h_{w\left(\theta \right)}\left(s\right)]\right|}_{s=x\cos \theta +y\sin \theta }d\theta .$$ (9)

We denote the filter's Fourier-domain transfer function as

$$H_{w\left(\theta \right)}\left(\omega \right)=\frac{\left|\omega \right|}{1+\frac{\beta }{w\left(\theta \right)}·\left|\omega \right|}.$$ (10)

The above discussion is under the assumption that the noise weighting w(θ) is a function of view angle θ. This view-by-view noise-weighting scheme can be extended to a ray-by-ray noise weighting scheme in an ad hoc manner.¹⁵ For ray-based noise weighting, w is a function of the ray: w = w(ray) = w(s, θ). At each view angle θ, we quantize the ray-based weighting function into n + 1 values: w₀, w₁, …, w_n, which in turn give n + 1 different filters as defined in Eq. 10. That is,

$$\begin{array}{c}\hfill H_k\left(\omega \right)=\left|\omega \right|/(1+\beta ·\left|\omega \right|/w_k),\mathrm{for}k=0,1,...,n.\end{array}$$ (11)

Using these n + 1 filters, n + 1 sets of filtered projections are obtained. Before backprojection, one of these n + 1 projections is selected for each ray according to its proper weighting function. Only one backprojection is performed using the selected filtered projections.

Spatial domain implementation

In general, if the spatial-domain kernel size is very small (e.g., in a three-point averaging filter) the spatial-domain implementation is faster. In tomography, the practical (ramp filter) kernel's size is twice the data size and the Fourier-domain implementation is faster. However, if the filter is spatially variant, the Fourier-domain method may not have an advantage. Let the detector size be N. If the filter is shift invariant, the spatial domain convolution takes O(N²) arithmetical operations, while the FFT/IFFT method computes can it with O(N log N) operations. However, if the filter is shift variant, the spatial domain implementation still takes O(N²) arithmetical operations, while the FFT/IFFT method computes it using O(N² log N) operations.

At the end of Sec. 2A, the spatially varying filter was implemented by Fourier-domain multiplication, using n + 1 filters with the help of quantization. In our previous implementations, the value n was selected as 10. Without using the quantization method, one would use 1024 filters to filter the projections 1024 times, if there were 1024 detection channels (or detection cells) on the detector. Therefore, it is not efficient to perform filtering in the Fourier domain if the filter is shift variant.

On the other hand, it is much more efficient if filtering is implemented in the spatial domain as integration when the kernel is spatially varying. If the integration kernel has a closed-form expression, the computation cost for spatial-domain filtering is the same as that of convolution, both using a dot product for implementation.

A routine method to find a discrete filter kernel h_w(n) is to evaluate the following integral,⁵ which is the 1D inverse Fourier transform of the transfer function defined in Eq. 10 with w(θ) replaced by w(s, θ) and s replaced by integer n:

$$\begin{array}{ccc}\hfill h_w\left(n\right)& =& \underset{-1/2}{\overset{1/2}{\int }}{H}_{w(s,\theta )}\left(\omega \right)e^{-i2\pi n\omega }d\omega \hfill \\ & =& 2\underset{0}{\overset{1/2}{\int }}\frac{\omega }{1+\frac{\beta }{w}·\omega }\cos \left(2\pi n\omega \right)d\omega ,\hfill \end{array}$$ (12)

where we used the property that the transfer function H_w(ω) is an even function. After quantization, w in Eq. 12 is w_k. It is unlikely that the integral in Eq. 12 has an explicit closed-form expression.

Our method is to find a finite expansion of the function H_w(ω) and the expansion should have closed-form inverse Fourier transform. Since 1 / (1 + β₀ω) with β₀ > 0 is a monotonically decreasing function on [0, 1/2], we have decided to use the following approximation:

$$\begin{array}{c}\hfill \frac{\omega }{1+{\beta }_0·\omega }\approx \frac{\omega }{3}(e^{-{\beta }_0\omega }+e^{-{\beta }_1\omega }+e^{-{\beta }_2\omega })\mathrm{with}{\beta }_0=\frac{\beta }{w},\end{array}$$ (13)

where the parameters β₁ and β₂ are to be determined. The range of ω is [0, 1/2]. The approximation Eq. 13 is already exact at ω = 0. We further request that Eq. 13 to be exact at ω = 1/4 and ω = 1/2. Thus, we have two unknowns (β₁ and β₂) and two equations:

$$\frac{1}{1+{\beta }_0/2}=\frac{1}{3}\left(e^{-{\beta }_0/2}+e^{-{\beta }_1/2}+e^{-{\beta }_2/2}\right),$$ (14)

$$\frac{1}{1+{\beta }_0/4}=\frac{1}{3}\left(e^{-{\beta }_0/4}+e^{-{\beta }_1/4}+e^{-{\beta }_2/4}\right).$$ (15)

Solving these two equations yields

$$\begin{array}{ccc}& & {\beta }_1=-4·\ln \left(\frac{A+\sqrt{2B-A^2}}{2}\right)\mathrm{and}\hfill \\ & & {\beta }_2=-4·\ln \left(\frac{A-\sqrt{2B-A^2}}{2}\right),\hfill \end{array}$$ (16)

where

$$\begin{array}{c}\hfill A=\frac{3}{1+{\beta }_0/4}-e^{-{\beta }_0/4}\mathrm{and}B=\frac{3}{1+{\beta }_0/2}-e^{-{\beta }_0/2}.\end{array}$$ (17)

Using the above results and an integral table, the closed-form filter kernel 12 can be obtained as (n ≠ 0):

$$\begin{array}{ccc}\hfill h_w\left(n\right)& =& \frac{2}{3}\underset{0}{\overset{1/2}{\int }}\omega (e^{-{\beta }_0\omega }+e^{-{\beta }_1\omega }+e^{-{\beta }_2\omega })\cos \left(2\pi n\omega \right)d\omega \hfill \\ & =& \frac{-2}{3}\sum _{k=0}^2\frac{{(-1)}^n{e}^{-\frac{{\beta }_k}{2}}\left({\beta }_k^3+4{\beta }_k{\pi }^2{n}^2+2{\beta }_k^2-8{\pi }^2{n}^2\right)-2{\beta }_k^2+8{\pi }^2{n}^2}{{\left({\beta }_k^2+4{\pi }^2{n}^2\right)}^2},\hfill \end{array}$$ (18)

and

$$h_w\left(0\right)=-\sum _{n\ne 0}{h}_w\left(n\right)=-\sum _{n=1}^2{h}_w\left(n\right).$$ (19)

The purpose of Eq. 19 is to guarantee that H_w(0) = 0. The filter kernel h_w(n) is an even function with respect to index n.

If we take the limit of β → 0, Eq. 18 reduces to

$$h\left(n\right)=\left\{\begin{array}{cc}\hfill 1/4& \hfill n=0\\ \hfill 0& \hfill n=\pm 2,\pm 4,\pm 6,...\\ \hfill -1/{\left(\pi n\right)}^2& \hfill n=\pm 1,\pm 3,\pm 5,...\end{array}\right.,$$ (20)

which is the well-known convolution kernel for the conventional ramp filter.

Selection of β and weights w

The newly derived FBP algorithm's filter kernel depends on β₀ = β/w(s, θ), which in turn depends on the Bayesian term control parameter β and the current ray weighting factor w(s, θ).

The principle of selecting both β and w(s, θ) is exactly the same as that for the Fourier-domain implementation. Both methods can use the same β and w(s, θ) values. There is a trade-off consideration for the objective function 1. A larger β value emphasizes the regularization Bayesian term more, and usually encourages a smoother image with a lower resolution. Setting β to zero or an extremely small positive value results in a high resolution but noisy image. As discussed in Ref. 16, the FBP algorithm is somewhat equivalent to an iterative algorithm with an iteration number of infinity. Also, when β = 0, the relative noise weighting is not effective. By “relative” we mean that the projection rays compete with each other, and some rays are emphasized while others are de-emphasized by assigning a set of weights w(s, θ), one for each ray. The weights are also relative, meaning that you can scale the weights w(s, θ) by a constant value. However, this scaling value affects the selection of the value of β. Usually, the weights w(s, θ) are selected as the reciprocal of the noise variance (or a function of the variance) of the projection.

One may argue that in an iterative algorithm the noise weighting is always effective, regardless whether there is a Bayesian term or not. When a system of linear equations is not consistent due to noise, noise weighting is commonly used to define an acceptable “solution.” When a linear system has a unique solution, the noise weighting should not affect the final (unique) solution. However, an iterative algorithm can only present a result with a finite number of iterations. Even though the final solution is unique, the noise weighting can alter the path towards to unique solution. Because the final solution is usually very noisy, early algorithm termination is the most common method for regularization. The effects of multiple convergent paths and early termination make the noise weighting effective in an iterative algorithm, regardless whether there is an explicit Bayesian regularization term or not. An effective regularization is always applied in one way or another.

One may ask under what conditions an imaging system can provide a unique (but maybe noisy) solution. An imaging system is usually modeled as an over-determined linear system, in which the number of unknowns (i.e., the image pixels) is less than the number of equations (i.e., the number of detection rays or cells or channels). Due to noise, this linear system is inconsistent and it does not have a solution. Let such a system be denoted in the matrix form as

$$AX=P,$$ (21)

where X is a vector contains all unknown image pixels, A is the projection matrix, and P is the array of noisy projections. However, its associated normal equation or weighted normal equation shown below, respectively, can give a unique least-squares solution:

$$A^{T}AX=A^{T}P\mathrm{or}{A}^{T}WAX=A^{T}WP,$$ (22)

where W is a certain weighting matrix. As discussed in Ref. 16, an FBP algorithm can be viewed as a solution to the least-squares problem, which is the unique solution to the “normal equation,” which is formulated in the continuous image domain.

The case of c = δ and g ≠ 0

In the case of c = δ and g ≠ 0, the Bayesian term encourages a solution f(x, y) that looks like g(x, y) as much as possible while satisfies the projections as much as possible. For this special situation, Eq. 3 becomes

$$\begin{array}{ccc}\hfill F({\omega }_x,{\omega }_y)& =& \frac{\sqrt{{\omega }_x^2+{\omega }_y^2}}{1+\beta ·\frac{\sqrt{{\omega }_x^2+{\omega }_y^2}}{w\left(\theta \right)}}\hfill \\ & & \times \left[B({\omega }_x,{\omega }_y)+\frac{\beta }{w\left(\theta \right)}·G({\omega }_x,{\omega }_y)\right].\hfill \end{array}$$ (23)

From the derivation in Sec. 2B, we conclude that the filter kernel h_w(n) for this case is the same as that defined in Eqs. 18, 19. The only change is to replace the projections p(s,θ) by the combined projections

$$p_{\mathrm{combined}}(s,\theta )=p(s,\theta )+\frac{\beta }{w\left(\theta \right)}·p_g(s,\theta ),$$ (24)

where the secondary data p_g(s, θ) are generated from the prior image g(x, y) by first performing forward projection and then ramp filtering.

The case of c being a Laplacian filter and g = 0

If the filter c in Bayesian term of Eq. 1 is not a delta function δ, but is a Laplacian filter, which is a second-order derivative filter and is usually used as an edge detector, this Bayesian term penalizes sharp edges and high frequency noise. The 1D Fourier transform of the Laplacian kernel is ω². Thus, the modified ramp filter for this case will have a Fourier-domain transfer function as

$$H_{w\left(\theta \right)}\left(\omega \right)=\frac{\left|\omega \right|}{1+\frac{\beta }{w\left(\theta \right)}·{\left|\omega \right|}^3}.$$ (25)

This function 25 has a faster high frequency gain drop-off rate than Eq. 10. Unfortunately, for this situation, the following approximation

$$\begin{array}{c}\hfill \frac{\omega }{1+{\beta }_0·{\omega }^3}\approx \frac{\omega }{3}\left(e^{-{\beta }_0\omega }+e^{-{\beta }_1\omega }+e^{-{\beta }_2\omega }\right)\mathrm{with}{\beta }_0=\frac{\beta }{w}\end{array}$$ (26)

is rather poor. The Taylor expansion approximation

$$\frac{\omega }{1+{\beta }_0·{\omega }^3}\approx \omega (1+a\omega +b{\omega }^2)\mathrm{with}{\beta }_0=\frac{\beta }{w}$$ (27)

is also poor if β₀ω > 1. A third option is the following expansion approximation

$$\begin{array}{c}\hfill \frac{\omega }{1+{\beta }_0·{\omega }^3}\approx \frac{\omega }{3}(e^{-{\beta }_0{\omega }^2}+e^{-{\beta }_1{\omega }^2}+e^{-{\beta }_2{\omega }^2})\mathrm{with}{\beta }_0=\frac{\beta }{w}.\end{array}$$ (28)

The range of ω is [0, 1/2]. The approximation 28 is already exact at ω = 0. We further request that Eq. 28 to be exact at ω = 1/2^4/3 and ω = 1/2. Thus, we have two unknowns (β₁ and β₂) and two equations:

$$\frac{1}{1+{\beta }_0/8}=\frac{1}{3}(e^{-{\beta }_0/8}+e^{-{\beta }_1/8}+e^{-{\beta }_2/8}),$$ (29)

$$\frac{1}{1+{\beta }_0/16}=\frac{1}{3}(e^{-{\beta }_0/16}+e^{-{\beta }_1/16}+e^{-{\beta }_2/16}).$$ (30)

Solving these two equations yields

$$\begin{array}{ccc}& & {\beta }_1=-16·\ln \left(\frac{A+\sqrt{2B-A^2}}{2}\right)\mathrm{and}\hfill \\ & & {\beta }_2=-16·\ln \left(\frac{A-\sqrt{2B-A^2}}{2}\right),\hfill \end{array}$$ (31)

where

$$\begin{array}{c}\hfill A=\frac{3}{1+{\beta }_0/16}-e^{-{\beta }_0/16}\mathrm{and}B=\frac{3}{1+{\beta }_0/8}-e^{-{\beta }_0/8}.\end{array}$$ (32)

It can be verified that the fit 28 is satisfactory. The problem is that the definite integral

$$\begin{array}{c}\hfill h_w\left(n\right)=\frac{2}{3}\underset{0}{\overset{1/2}{\int }}\omega (e^{-{\beta }_0{\omega }^2}+e^{-{\beta }_1{\omega }^2}+e^{-{\beta }_2{\omega }^2})\cos \left(2\pi n\omega \right)d\omega \end{array}$$ (33)

can only be expressed in terms of the special function erf called the “error function.” One could use a lookup table for the function erf or use further approximation of the function erf.

To date we do not yet have any good results for this special case: either the fits 26, 27 are poor, or the inverse Fourier transform 33 does not have a closed-form expression. The example in Sec. 2E shows that the spatial-domain filtering method developed in Sec. 2B is not universal, and it can be inefficient if no closed-form kernels are available. In this case, it is better to use the Fourier-domain filtering.

Kernel for curved-detector fan-beam FBP algorithm

The discussion so far is about the development of a modified ramp filter that is suitable for the parallel-beam or flat-detector fan-beam imaging geometries. For the curved-detector fan-beam imaging geometry, its convolution kernel h_curve(n) is a scaled version of the parallel-beam or the flat-detector fan-beam geometry's convolution kernel h(n):⁵

$$h_{\mathrm{curve}}\left(n\right)={\left[\frac{n/D}{\sin (n/D)}\right]}^{2}h\left(n\right),$$ (34)

where D is the fan-beam focal length. Applying the curved-detector fan-beam relationship 34 to the newly developed noise-weighted kernel 18 yields

$$h_{\mathrm{curve},w}\left(n\right)=\frac{-2}{3}{\left[\frac{n/D}{\sin (n/D)}\right]}^2\sum _{k=0}^2\frac{{(-1)}^n{e}^{-\frac{{\beta }_k}{2}}\left({\beta }_k^3+4{\beta }_k{\pi }^2{n}^2+2{\beta }_k^2-8{\pi }^2{n}^2\right)-2{\beta }_k^2+8{\pi }^2{n}^2}{{\left({\beta }_k^2+4{\pi }^2{n}^2\right)}^2}.$$ (35)

IMPLEMENTATION AND DATA SETS

Implementation of the proposed FBP algorithm

Like the conventional convolution backprojection FBP algorithm, the proposed FBP algorithm first filters the projection data with a spatially variant, noise weighted, ramp filter, and the filtering is performed in the spatial domain by evaluating a dot product. The filtered data are then backprojected into the image domain. Since the backprojection procedure of our algorithm is identical to the conventional backprojection, we only discuss the discrete implementation of the filtering procedure below.

We denote the discretely sampled projections as p_d(n, m), where n is the index on the detector and m is the index of the view angle. We use a subscript d to indicate discretely sampled functions. For any fixed view angle m, do the following:

Loop through the detector cell index n:

• Step 1: Consider the noise model of p_d(n, m) and estimate the variance of the measurement p_d(n, m). Let the weighting factor w_d(n, m) be the reciprocal of the variance (or a function of the variance).

• Step 2: Evaluate the spatial-domain filter kernel h_w(n) according to Eqs. 18, 19.

• Step 3: Calculate filtered projection value q_d(n, m) using a dot product:

$$q_d(n,m)=\sum _k{h}_w(k-n)·p_d(k,m).$$ (36)

Next n.

In forming the spatial-domain filter kernel h_w(n), one needs to select a Bayesian term control parameter β. A larger β gives a smoother and less noisy image. This value is chosen by trial-and-error and by incorporating with the selection of the weighting function w.

Low-dose cadaver CT data

To illustrate the feasibility of the proposed spatial-domain filtering FBP algorithm, a cadaver torso was scanned using an x-ray CT scanner with a low-dose setting. Data were collected with a diagnostic scanner (Aquilion ONE^TM, Toshiba America Medical Systems, Tustin, CA; raw data courtesy of Leiden University Medical Center).

The imaging geometry was curved-detector cone-beam, the x-ray source trajectory was a circle of radius 600 mm. The detector had 320 rows, the row-height was 0.5 mm, each row had 896 channels, and the fan angle was 49.2°. A low-dose noisy scan was carried out. The tube voltage was 120 kV and current was 60 mA. There were 1200 views uniformly sampled over 360°. The reconstructed image array was 840 × 840 and the image resolution was 0.5 mm. The noise weighting factor for this data set was chosen as w = exp(−0.3 p), where p is the line-integral measurement. The Bayesian term control parameter β was chosen as 1.0 × 10⁻⁷.

Only the central slice of image volume was reconstructed. The images were reconstructed by the conventional fan-beam FBP algorithm without noise weighting and by the proposed FBP algorithm with noise weighting using spatial-domain modified ramp filtering.

Computer simulations

An analytical image reconstruction algorithm uses a low-pass filter to adjust the trade-off between the noise (and artifact) and spatial resolution. Some spatial resolution is lost when some noise is suppressed. We argue that the iterative image reconstruction algorithms have the similar trade-off effects. To illustrate this point, an iterative weighted Landweber algorithm was also implemented for the comparison purposes.²²

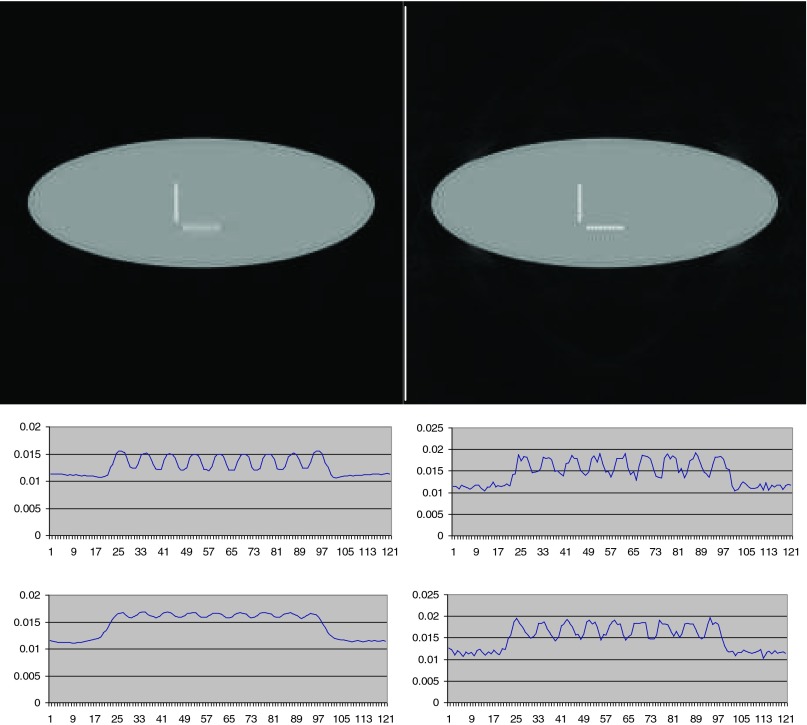
We used a computer generated phantom that contained a row and a column of small dots (see Fig. 3). The projection line integral data were generated analytically noise-free. The motivation of using a noise-free data set is to better study the spatial resolution degradation effects of the reconstruction algorithms. There were 1200 views uniformly sampled over 360°. There were 896 detection channels on the detector. The reconstructed image array was 840 × 840 and the image resolution was 0.5 mm. Even though the data were noise-free, the noise weighting factor for this data set was chosen as w = exp(−0.3 p), where p is the line-integral measurement. The same noise weighting factor was used for both the weighted FBP algorithm and the iterative Landweber algorithm. The weighted FBP algorithm used the exactly same parameters that had been chosen for the clinical data stated in Sec. 2B. Both ray-by-ray noise weighting and view-by-view noise weighting methods were presented. In the view-by-view weighting method, the maximum line-integral p for each view was chosen to determine the weighting factor for every ray in this view. The iterative algorithm used two different numbers of iterations: 500 and 5000, respectively.

Figure 3.

Images reconstructed using noiseless computer simulated data. (First column) Conventional convolution backprojection reconstruction. (Second column) Proposed noise-weighted FBP reconstruction with spatial-domain filtering using ray-by-ray weighting. (Third column) Noise-weighted FBP reconstruction with spatial-domain filtering using view-by-view weighting. (First row) Display with a full gray-scale from minimum to maximum for each image. (Second row) Line profiles along the horizontal small dots. (Third row) Line profiles along the vertical small dots.

RESULTS

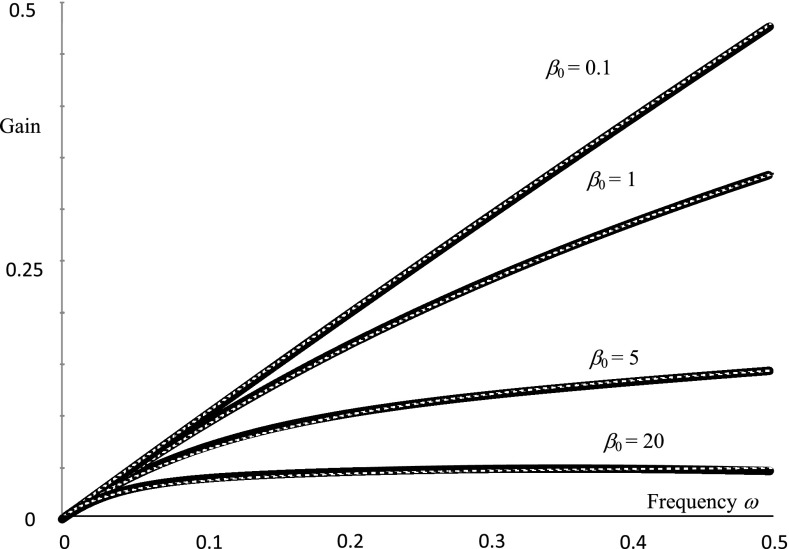
Figure 1 shows the Fourier-domain transfer functions of four filters according to approximation 13, for β₀ = 0.1, 1, 5, and 20, respectively. The original functions represented by the left-hand side of Eq. 13 are shown in solid curves, and the three-term expansions represented by the right-hand side of Eq. 13 are shown in dotted curves. Approximations are shown to be fairly accurate, and more accurate approximations are obtained for smaller β₀ values.

Figure 1.

Four pairs of Fourier-domain transfer functions according to approximation 13. The original functions represented by the left-hand side of Eq. 13 are shown in solid curves and the three-term expansions represented by the right-hand side of Eq. 13 are shown in dotted curves.

Since an accurate approximation is usually achieved in a small region close to a point of interest, for example, about β₀ω = 0. In order to obtain a good approximation in a large region with only few terms, it is important to select the basis functions that look similar to the original functions to be expanded. This was the reason that we chose $\left\{e^{-{\beta }_k\omega }\right\}$ to expand 1/(1 + β₀ω), and $\left\{e^{-{\beta }_k{\omega }^2}\right\}$ to expand 1/(1 + β₀ω³). This was also the reason that we did not use Taylor expansion for 1/(1 + β₀ω) or 1/(1 + β₀ω³), because when β₀ω > 1 the approximation errors are large. Unfortunately, the functions $\left\{e^{-{\beta }_k{\omega }^2}\right\}$ or $\left\{\omega e^{-{\beta }_k{\omega }^2}\right\}$ do not have closed-form inverse Fourier transform expressions.

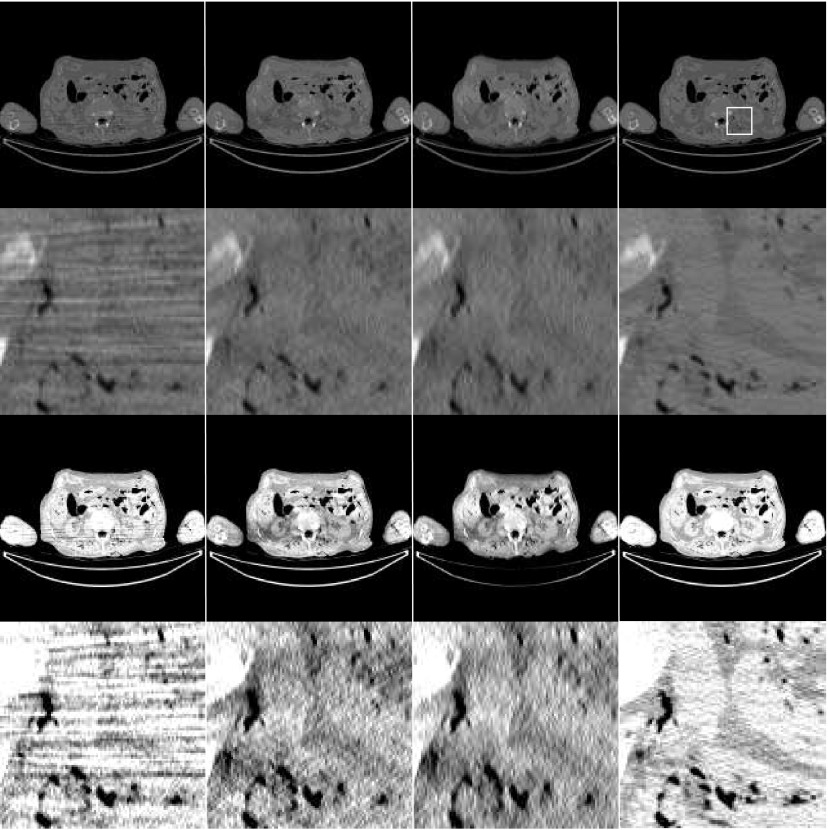
Figure 2 (first column) shows the conventional (i.e., without noise weighting) fan-beam convolution backprojection reconstruction of a transverse slice in the abdominal region of the cadaver. The x-rays through the arms are attenuated more than x-rays in other orientations, and create the left-to-right streak artifacts in the middle of the image. Figure 2 (second column) shows the reconstruction result using the proposed noise-weighted FBP with spatial-domain filtering implementation, using ray-by-ray weighting. The streak artifacts are effectively removed. Figure 2 (third column) is the same as the second column except that the view-by-view weighting is used. Figure 2 (fourth column) is the gold standard image, which is the conventional fan-beam convolution backprojection reconstruction using the standard dose CT data. The tube voltage was 120 kV and current was 500 mA.

Figure 2.

Images reconstructed using low-dose CT clinical cadaver data. (First column) Conventional convolution backprojection reconstruction. (Second column) Proposed noise-weighted FBP reconstruction with spatial-domain filtering using ray-by-ray weighting. (Third column) Noise-weighted FBP reconstruction with spatial-domain filtering using view-by-view weighting. (Forth column) Gold-standard: conventional convolution backprojection reconstruction using regular-dose CT data. (First row) Display with a full gray-scale from minimum to maximum for each image. (Second row) Zoom-in of the first row; the region-of-interest is indicated in the upper-right image. (Third row) Display of the first row with a narrower gray-scale window. (Forth row) Display of the second row with a narrower gray-scale window.

Figures 34 show the reconstruction results of the computer simulation data with the FBP algorithms and the iterative algorithm, respectively. Line profiles are drawn across the row and column of the small dot to compare the resolution degradation. The vertical line profiles show worse resolution degradation because a narrower low-pass filter window is used in that direction according to the noise model. In the weighted FBP algorithm, a larger line integral p associates with a narrower window. The ray-by-ray weighting and the view-by-view weighting have similar effects.

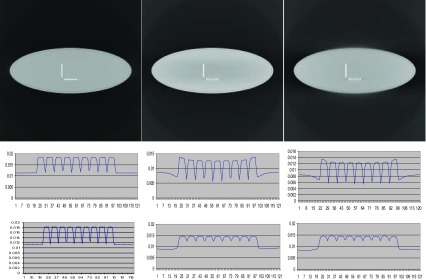
Figure 4.

Images reconstructed by iterative weighted Landweber algorithm using noiseless computer simulated data. (First column) 500 iterations. (Second column) 5000 iterations. (First row) Display with a full gray-scale from minimum to maximum for each image. (Second row) Line profiles along the horizontal small dots. (Third row) Line profiles along the vertical small dots.

In the iterative algorithm results with 500 iterations, we can make the same observation: the vertical line profile shows worse spatial resolution than the horizontal profile. This is because the iterative algorithm improves the spatial resolution as the iteration number increases. The noise weighting factors control the step sizes of image update at each iteration. A larger weight causes faster convergence rate of resolution recovery. Nonconstant weights cause nonuniform resolution.

When the iteration number approaches to infinity, the algorithm will converge to a final image with uniform spatial resolution. In this situation, the noise will be amplified and the image will be too noisy to be useful in practice. Like the analytic algorithm, the iterative algorithm also uses the noise/resolution trade-off relationship to suppress noise by sacrificing some resolution.

CONCLUSIONS

This paper developed a spatial-domain implementation method for our previously proposed noise-weighted FBP algorithm. Owing to the spatially variant nature of noise weighting, the filter in the FBP algorithm varies from ray to ray and it is not very efficient to implement it in the Fourier domain.

We have a closed-form representation for the filter's Fourier domain transfer function; however, we do not have a closed-form representation for its spatial domain counterpart. We agree that one could always use the “numerical” spatial-domain kernel that is obtained by taking the inverse Fourier transform of the known transfer function. Since our filter is spatially variant, this numerical approach is not computationally efficient. If we chose this approach, there would be no advantage to implement the filtering procedure of an FBP algorithm in the spatial main.

Our “second best” solution is to derive an approximate, closed-form, spatial-domain kernel. There is no theoretical base that a three-term exponential function is the optimal selection for this “second best” solution. We chose the exponential function because the numerically obtained spatial-domain kernel visually looks an exponential function. Why three terms? Because we found that three terms are accurate enough to approximate the numerically obtained kernel.

In spatial-domain implementation, filtering is achieved by performing a dot product of the projections with an integration kernel. This kernel function is discrete for a discrete implementation. To be efficient (meaning, fast computation), we require the kernel have an explicit closed-form expression. It is unlikely that the noise-weighted ramp filter |ω|/(1 + β₀|ω|) has a closed-form inverse Fourier transform, but it can be accurately approximated by $(\left|\omega \right|/3)·(e^{-{\beta }_0\left|\omega \right|}+e^{-{\beta }_1\left|\omega \right|}+e^{-{\beta }_2\left|\omega \right|})$, which has a closed-form inverse Fourier transform expression. Thus, an explicit expression of the integral kernel can be obtained.

This approach of obtaining a closed-from integration kernel is not universal. We gave a counter-example of a noise-weighted ramp filter |ω|/(1 + β₀|ω|³), for which we were unable to find a closed-from integration kernel.

The noise-weighted FBP algorithm and the iterative gradient algorithm are two approaches that try to minimize the same quadratic objective function. They have their own advantages and disadvantages. The noise-weighted FBP algorithm is faster, while the iterative algorithm can better model the projection physics. We have reported some results to compare these two approaches.^{17, 20} Unfortunately, for few-view applications, the FBP algorithms including noise-weighted FBP algorithm do not perform well.