Semiautomatic segmentation and follow-up of multicomponent low-grade tumors in longitudinal brain MRI studies

Abstract

Purpose: Tracking the progression of low grade tumors (LGTs) is a challenging task, due to their slow growth rate and associated complex internal tumor components, such as heterogeneous enhancement, hemorrhage, and cysts. In this paper, the authors show a semiautomatic method to reliably track the volume of LGTs and the evolution of their internal components in longitudinal MRI scans.

Methods: The authors' method utilizes a spatiotemporal evolution modeling of the tumor and its internal components. Tumor components gray level parameters are estimated from the follow-up scan itself, obviating temporal normalization of gray levels. The tumor delineation procedure effectively incorporates internal classification of the baseline scan in the time-series as prior data to segment and classify a series of follow-up scans. The authors applied their method to 40 MRI scans of ten patients, acquired at two different institutions. Two types of LGTs were included: Optic pathway gliomas and thalamic astrocytomas. For each scan, a “gold standard” was obtained manually by experienced radiologists. The method is evaluated versus the gold standard with three measures: gross total volume error, total surface distance, and reliability of tracking tumor components evolution.

Results: Compared to the gold standard the authors' method exhibits a mean Dice similarity volumetric measure of 86.58% and a mean surface distance error of 0.25 mm. In terms of its reliability in tracking the evolution of the internal components, the method exhibits strong positive correlation with the gold standard.

Conclusions: The authors' method provides accurate and repeatable delineation of the tumor and its internal components, which is essential for therapy assessment of LGTs. Reliable tracking of internal tumor components over time is novel and potentially will be useful to streamline and improve follow-up of brain tumors, with indolent growth and behavior.

INTRODUCTION

Accurate quantification of gross tumor volume is an important factor in the assessment of therapy response in patients with brain tumors.¹ For many types of brain tumors, such as optic pathway gliomas (OPGs) and other forms of astrocytoma, it is also important to quantify the volume of the different tumor components, e.g., cysts, enhancing patterns, edema, and necrotic regions.^{2, 3, 4} Volumetric quantification over time of gross total volume changes and internal tumor transformations serve as important measures for clinical decisions. The need for an accurate and repeatable method for tumor volume quantification is evident in low grade tumors (LGTs), where the tumor growth rate is relatively slow⁵ and the follow-up evaluation is based on small changes in the tumor and its internal components over time.

MRI is the method of choice for therapy assessment of brain tumors. The most commonly used definitions of radiological follow-up and response to treatment are based on linear measurements defined by WHO, RECIST, MacDonald, and RANO criteria.^{1, 6, 7} The main drawback of linear measurements is that they do not reflect reliable volumetric changes, when these occurred outside of the axes of the linear measurements. In addition, they are highly user-dependent so the comparison between two different imaging studies is difficult. Due to the variability among readers, the criteria specify large changes in linear measure that separate the different categories of response assessment. Consequently, current methods are less sensitive to detecting a response than a potential quantitative method that can reliably detect a smaller change. Finally, reliable tracking of the tumor's internal components' evolution over time is almost impossible using these criteria.

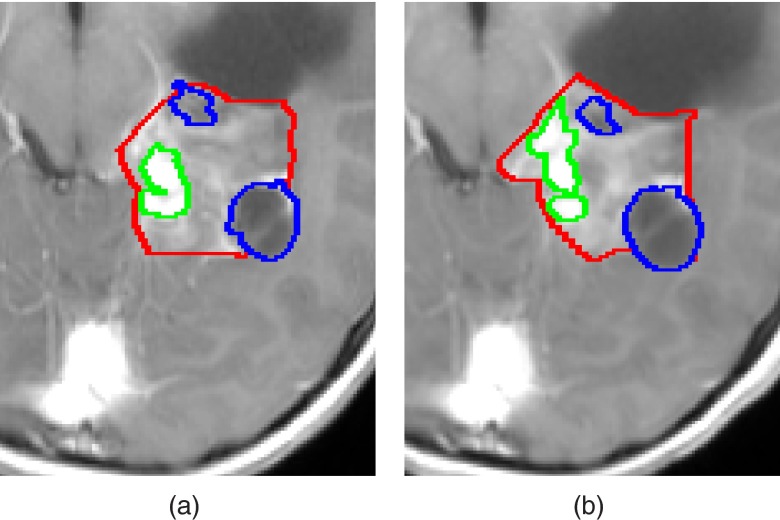
Manual quantification of brain tumor volume, although considered the gold standard, is time consuming and may suffer from inconsistencies of the delineated tumor boundaries between and within observers over time.⁸ This phenomenon, known as inter/intraobserver variability, may mislead the evaluation of tumor progression and can result in improper treatment decisions. In addition, the inter/intraobserver variability is likely to increase in cases where tumor boundaries appear unclear due to the surrounding tissues with overlapping signal intensity values, the uneven tumor infiltration into nearby structures, and the imaging partial volume effect. An example is shown in Fig. 1.

Figure 1.

Manual delineations of LGT internal components, performed by the same observer, overlaid on a representative slice of T1c image from (a) a baseline scan, and (b) a follow-up scan. Solid, enhancing and cyst components are presented. Note that some of the LGT components boundaries were delineated differently in each scan despite slight changes in the scans.

A variety of automatic methods for the segmentation and classification of brain tumors have been recently published.^{3, 9, 10, 11, 12} The International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI) hosts an annual Multimodal Brain Tumor Segmentation (BraTS) challenge,^{13, 14} in which different segmentation strategies for brain tumors are evaluated. While effective, most of these methods are evaluated for independent MR scans and do not take into account prior information from previous scans of the same patient. Therefore, when applied on two consecutive scans over time, they may not reproduce the same tumor boundaries even when the scans are very similar to each other and even when there is no actual change in the tumor in those areas.

Quantification of longitudinal changes in brain MRI scans has gained much attention in recent years.^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24} Some of these methods register follow-up MR scans and analyze the changes between the scans. Patriarche and Erickson²² present a gray-level based change detection. Elliott et al.¹⁷ define a Bayesian framework to overcome the registration artifact problem of subtracting two consecutive scans. Angelini et al.¹⁵ address the nonlinear contrast change between the two data sets with normalization via midway histogram equalization. Chitphakdithai et al.¹⁶ simultaneously estimate the registration parameters and label the changes between two consecutive brain scans to track metastatic brain tumors. Pohl et al.²³ present a pipeline method to segment a tumor in a set of longitudinal scans based on user guided segmentation of the first scan. Menze et al.¹⁰ and Konukoglu et al.²⁵ present approaches for modeling tumor growth in longitudinal images based on a reaction-diffusion framework.²⁶ Additional works of Das et al.,²⁷ Xu et al.,²⁸ and Bernal-Rusiel et al.²⁹ perform longitudinal analysis of volumetric changes of various structures in the brain and the body.

An important issue in brain tumors analysis is the role of various components of the within the tumor, e.g., necrotic, enhancing, and cystic regions. While this issue is addressed in BraTS (Refs. ¹³ and ¹⁴) and few other works,^{9, 30} tracking the tumor's internal components over time has gained less attention. Reliable follow-up of the evolution of the tumor's internal components (e.g., cyst, enhancing regions, edema) serves as an important factor in the treatment efficacy evaluation. In many cases, the transformation of one component into another indicates tumor progression or response to treatment, even when the gross total volume of the tumor remains the same.⁴

In this paper, we focus on the longitudinal assessment of LGTs internal components. These tumors have a relatively slow growth rate,³¹ and therefore require accurate and repeatable volumetric follow-up for therapy assessment. We describe a new approach for the segmentation and internal components classification of LGTs in longitudinal scans. The basic premise of our method is that prior based knowledge of baseline segmentation of the tumor components is essential for the segmentation of the subsequent scan in the time series, as it provides high-quality prior information for the following scan.

Our previous publications^{32, 33} present a method for the segmentation and internal components classification which was restricted to OPG, based on its unique location in the brain, in a single MR scan where no information is shared between time points. In this paper, we present a general method for LGT internal components segmentation in longitudinal studies that uses the segmentation of the previous time point as a prior knowledge to track the evolution internal tumor components reliably.

A brief description and preliminary results of the method were published in a conference.³⁴ In this paper, we extended Sec. 2 to include detailed description of the theoretical models and the estimation of their unknown parameters. In addition, we expanded Sec. 3 to include new datasets with two types of LGTs.

The main contributions of this paper are: (1) the use of a baseline delineation of tumor components to increase the reproducibility of the resulting follow-up; (2) a spatiotemporal model for tumor internal components transitions over time; (3) segmentation and tracking of the internal components of LGTs; and (4) the evaluation on two types of LGTs in follow-up studies, resulting in a robust and consistent follow-up tool.

This paper is organized as follows. Section 2 presents the method for LGTs segmentation and internal tumor components classification in follow-up scans. Section 3 describes the experimental results. Section 4 discusses the method and its results; Sec. 5 concludes by highlighting the key findings of the research.

METHOD

The inputs to our method are two consecutive MRI scans of the same patient: a baseline scan and a follow-up scan, denoted as V_B and V_F. Each scan consists of several MR images, e.g., T1-weighted (T1W), T2-weighted (T2W), among others. The baseline scan includes a radiologist-approved delineation of the tumor boundary and its components, denoted as C_B. The output is a multilabel classified set of voxels that represents the tumor components in the follow-up scan, C_F.

Our method relies on a reliable delineation of the tumor in the baseline scan of the patient. While this paper does not address the tumor segmentation in the baseline scan, this delineation can be performed manually, semiautomatically, or fully automatically for specific types of tumors. Semi- or fully automatic methods for various brain tumors have been addressed by us^{32, 33} and others.^{3, 9, 10, 11, 13, 14, 18, 24, 35} This issue is further discussed in Sec. 4.

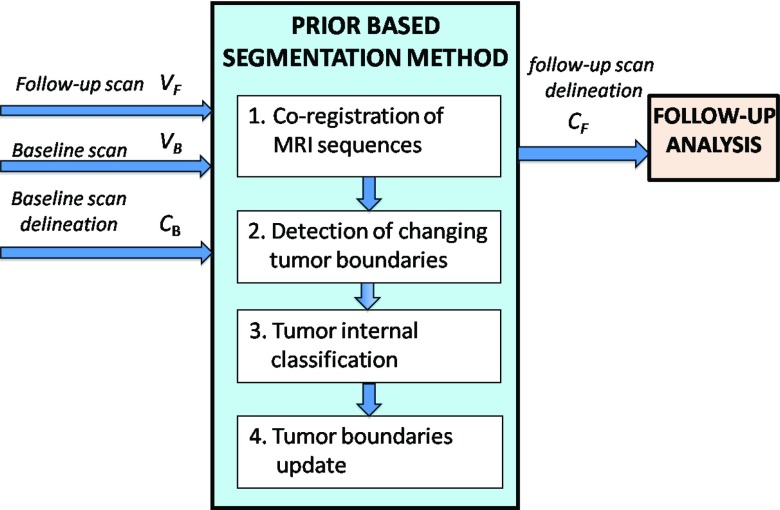
Figure 2 shows a flow chart of our method. The method consists of four steps. In step 1, the MR images of every scan are coregistered to a representative image within that scan, followed by coregistration of the follow-up scan to the baseline scan. In step 2, the input tumor boundaries of the baseline scan are overlaid on the follow-up scan to detect boundary segments that have changed. In step 3, the internal classification of the overlaid tumor area is computed from the follow-up scan data. In the fourth step, the detected boundary segments from step 2 are updated using the result of step 3. Figure 3 shows a representative example of the resulting follow-up classification of an OPG vs ground truth.

Figure 2.

A flow chart of the proposed method. A baseline scan, V_B, its corresponding tumor components delineation, C_B, and a follow-up scan, V_F are fed into the system. Our four-step method's output is C_F, which is segmentation of the tumor and its internal components in the follow-up scan.

Figure 3.

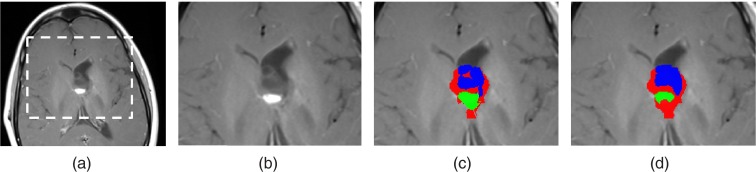
(a) A representative slice of T1c image from a follow-up scan. (b) An enlarged view of the tumor area. (c) Algorithm results and (d) manually delineated ground truth of OPG classified into solid, enhancing and cyst components.

Step 1: Coregistration of MRI sequences

Each MRI scan consists of several imaging contrasts. In our experiments, each scan consisted of T2-weighted and contrast-enhanced T1 imaging contrasts. The imaging contrasts comprising each scan were rigidly registered, to compensate for patient movements during acquisition. Then, we rigidly registered the follow-up scans to their corresponding baseline scans.³⁶ Thanks to the fact that LGTs are slow growing and no major changes appear between time-points, rigid registration was found to be adequate for this purpose.

The result is registered baseline and follow-up scans. We denote the baseline scan and registered follow-up scan as V_B and ${\tilde{V}}_F$, respectively.

Step 2: Detection of changing tumor boundaries

In this step, we detect the tumor boundary segments that have changed between the baseline and the follow-up scans. We first classify the input tumor boundaries into sharp boundaries and fuzzy boundaries. To compensate for inaccuracies in the manual input boundaries, we use a hybrid method to perform this classification.

For every slice in the baseline segmentation, the input tumor boundary is divided into segments of K voxels each. The value of K is determined by the nature of the tumor and the spatial dimensions of the data. Then, for every boundary segment, the surrounding area with a fixed radius, r_T, around the center of the segment is partitioned into two clusters with the k-means algorithm. Note that the k-means algorithm operates on a vector of images (e.g., T1W, T2W, FLAIR) for each voxel.

A boundary segment is marked as sharp if the clusters surrounding it satisfy the following two conditions:

• 1.The gray-levels based overlap between the clusters, defined by the Davies-Bouldin index test for overlap,³⁷ is below a predefined threshold, γ.
• 2.Every cluster lies on a different side of the boundary segment. To compensate for inaccuracies in the manual input boundaries, we relax this condition by allowing a small ratio of the voxels in each cluster to lie on the opposite side of the boundary. This ratio is controlled by a predefined parameter, 0 < α ⩽ 1.

When these two conditions are not satisfied, the boundary segment is marked as fuzzy. The values of the unknown parameters in this step, K, r_T, α, and γ are learned from a training set as explained in Sec. 3. The input segmentation of the baseline scan is then overlaid on the follow-up scan and the process is repeated for the follow-up scan. Figures 4a, 4b illustrate the sharp and fuzzy boundaries of the tumor in the baseline and follow-up scans.

Figure 4.

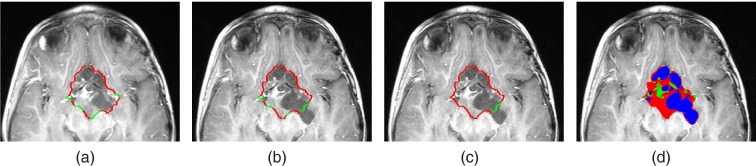
(a) and (b) Sharp and fuzzy boundary segments of the input baseline segmentation, overlaid on T1c image of baseline (a) and follow-up (b) scans. (c) shows the fixed and changing boundary segments of the baseline input segmentation overlaid on the follow-up scan. (d) presents the boundary of the tumor in the follow-up scan, after updating the boundary segments and delineating the voxels into solid enhancing and cyst tumor component.

Only boundary segments that are detected as sharp in the baseline scan and fuzzy in the follow-up scan are considered as changing boundaries and will be updated in further steps. We do not update sharp boundary segments in the follow-up scan as we consider them to represent the real boundary of the tumor. In addition, we do not update boundary segments that are detected as fuzzy in both baseline and follow-up scans to maintain the manual delineation in those regions and to avoid inter/intra observer variability.

Figure 4c shows an example of the fixed and changing boundary segments.

Step 3: Tumor internal classification

As previously noted, segmentation and follow-up of the internal tumor components is of major importance for tracking the tumor evolution and grade. Therefore, this step focuses on extracting the gray level distribution parameters of each tumor component. These will allow modeling of the tumor appearance in the follow-up scan which will be followed by updating the tumor's boundary segments in step 4.

Modeling tumor components gray levels distribution

We describe a model for representing LGT gray-levels distribution in the follow-up scan. The number of possible tumor components, N_C, is determined in advance, depending on the tumor type, from the clinical literature. For example, three components were chosen for OPG according to its phenotype: enhancing, solid nonenhancing, and cyst components. Note that the actual number of components at a given scan is patient dependent and may be smaller than N_C.

There are various ways to model tumor gray level intensities in MRI, such as Gamma¹¹ or Gaussian^{38, 39} distributions. Due to the unique pattern of LGTs that often involve several tumor components, we model the LGT gray-levels distribution with Gaussian Mixture Model (GMM), where each Gaussian represents a tumor component. The number of Gaussians, Q, represents the actual number of components in the scan and varies between 1 and N_C. Let ${\{a_q,{\mu }_q,C_q\}}_{q=1}^Q$ denote the GMM mixture proportion coefficients, mean vectors, and covariance matrices. The probability density function (pdf) of the gray-levels of the tumor in the follow-up scan is therefore formulated as GMM pdf

$$\begin{array}{ccc}& & f\left({\tilde{V}}_F\left(i\right)\right)\hfill \\ & & =\sum _{q=1}^Q{a}_q·\frac{\text{exp}\left\{-\frac{1}{2}{({\tilde{V}}_F\left(i\right)-{\mu }_q)}^T{C}_q^{-1}({\tilde{V}}_F\left(i\right)-{\mu }_q)\right\}}{{\left(2\pi \right)}^{J/2}{\left|C_q\right|}^{1/2}},\hfill \end{array}$$ (1)

where J is the number of images (T1c, T2w, etc.) in the scan.

Modeling tumor components temporal transitions

We develop a temporal tumor components transition model that describes the tumor internal components transitions over time. Note that the GMM parameters cannot be estimated directly from the baseline scan due to gray-level differences between scans. In addition, gray-level normalization of the follow-up images is undesirable, as it is ill-defined and thus error prone. Instead, we derive a temporal model for tumor components transitions over time. The purpose of this model is twofold: (1) to estimate the GMM parameters from the follow-up scan itself (and avoid temporal gray-scale normalization which might be error prone) and (2) to derive an internal components classification map for the follow-up scan which is consistent with the baseline segmentation.

Let p_ij denote the probability that a voxel belongs to an internal tumor component i in the baseline scan, and j in the follow-up scan. The components transition matrix

$$P={\left\{p_{ij}\right\}}_{i,j=1}^{N_C}$$ (2)

describes the probability that a given component, i, will turn into another component, j. The matrix P is defined for each tumor type. Since the probability of transitioning from state i to another state must be 1, P is a right stochastic matrix, whose elements satisfy

$$\sum _j{p}_{ij}=1\forall i1\le i\le N_C.$$ (3)

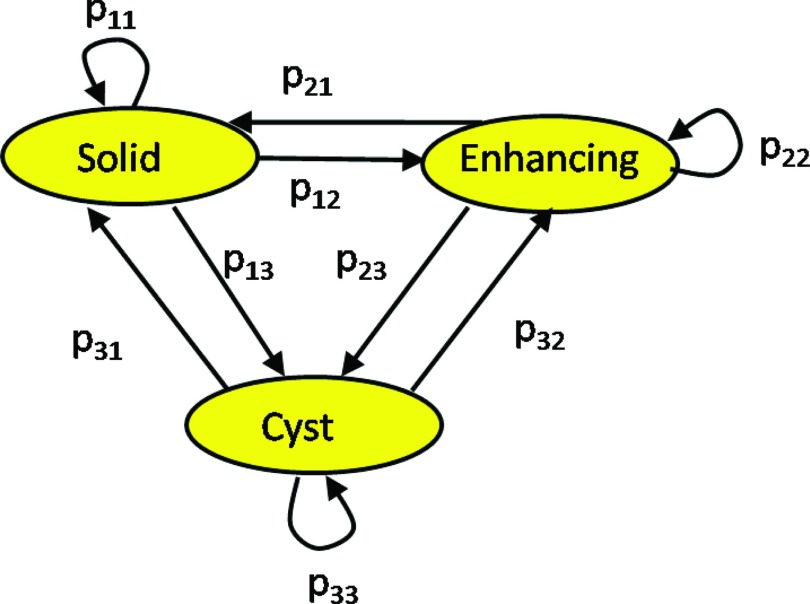
Figure 5 shows a graphical description of the model. We do not include a “healthy” component due to the low prevalence of such transitions in LGT.⁴⁰ Instead, we assume that tumors and healthy tissues have different gray levels, and as a result, healthy voxels will be eliminated in the final step of the algorithm (step 4). This issue is further discussed in Sec. 4.

Figure 5.

A transition model for three tumor components in its graphical (left) and matrix (right) forms. It describes the probability of a tumor component to change its state between a baseline follow-up scans. The nodes represent the tumor components and the edges are the transition probabilities.

Note that the tumor components transitions depend also with other parameters, such as: the time between the baseline and the follow-up scans, the undergoing treatment, the age of the patient, etc. However, due to the lack of a sufficient number of patients to reliably estimate all the other disease factors, we take into account only the influence of the dominant factor, which is the tumor type.

An extension of this transition model to include an additional dependency with the time between scans is given in the Appendix. The extension is applicable for cases where the time gap between consecutive follow-up scans varies, and the time independent model may not be suitable. The extended model was used to obtain the experimental results presented in this paper, due to uneven time gaps between follow-up scans time points in our data.

Model parameters estimation

Transition matrix estimation

There are two ways to define the elements of the matrix P. The first is based on prior knowledge about the nature of the specific tumor type. For example, in OPG, a solid component is much more likely to turn into an enhancing component than into a cyst. The second is estimating the elements of P using training data, as follows.

We assume that we have manually annotated tumor components classification maps of baseline-follow-up pairs. The probability of transition from state i to state j is estimated as the ratio of such transitions in the entire training set. We denote the total number of voxels used for training as N_v and the baseline and follow-up voxels in the training segmentation maps as v_B and v_F, respectively. The elements of P are then estimated by

$${\widehat{p}}_{ij}=\frac{1}{N_v}\sum _{l=1}^{N_v}\delta (v_B\left(l\right),i)\delta (v_F\left(l\right),j),$$ (4)

where l is an index representing spatial location and δ(·) is the Kronecker delta function.

Gaussian distributions parameters estimation

The unknown parameters of the GMM model are: the proportion coefficients, a_q, the mean vectors, μ_q, the covariance matrices, C_q, the number of Gaussian, Q, and the assignments of the tumor components to a Gaussian.

We estimate the unknown parameters of the Gaussian distributions for every 1 ⩽ Q ⩽ N_C using expectation maximization (EM) with the data of the follow-up scan itself. A detailed description of the implementation of EM for the estimation of GMM parameters is thoroughly explained by Gupta and Chen.⁴¹ In our implementation we used their method, where we initialize the EM algorithm with the baseline segmentation to obtain a solution which is consistent with the baseline segmentation. The set of estimators is denoted by ${\{\widehat{a_q},\widehat{{\mu }_q},\widehat{C_q}\}}_{q=1}^Q$, where Q varies between 1 and N_C. We then assign a single Gaussian to each follow-up scan voxel in the baseline tumor area, using the maximum a posteriori (MAP) estimation method where we assume equal prior probability on q. This results in clustering the follow-up scan voxels into Q clusters. Since Q ranges between 1 and N_C, the result is N_C clusters maps.

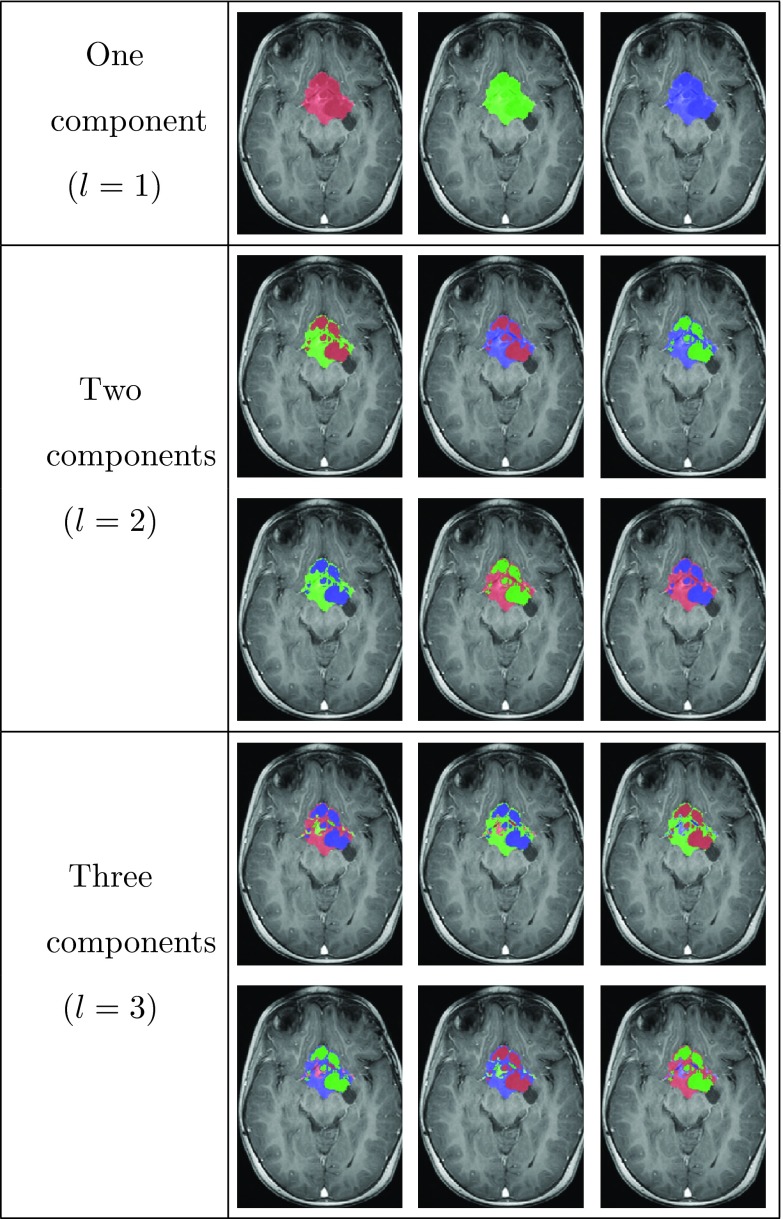
Note that at this stage we have not yet assigned a specific tumor component to a Gaussian, as we avoid relying on gray-level intensities for this purpose. Instead, we assign all the available permutations of labels to the resulting clusters maps, to obtain classification map candidates. Figure 6 shows an example of the 15 classification map candidates for OPG with a maximal number of components N_C = 3. These maps are denoted by ${\left\{C_m\right\}}_{m=1}^M$, where M denotes the number of classification maps candidates.

Figure 6.

Follow-up classification map candidates, C_m for N_C = 3 components, overlaid on T1c image of the follow-up scan.

When the tumor components characteristics are known a priori, it may be possible to reduce the number of classification map candidates. For example, in the case of OPG, cyst areas appear dark in the FLAIR image and hyperintense in the T2W image. However, we ignore this type of a priori knowledge as we would like to develop a general method that is also suitable for situations in which this a priori knowledge is not available or unknown, and to handle cases in which different components have similar gray level values in the provided images.

Next, we rely on the assumption that classification map pixels are independent and formulate the probability that C_m represents the correct classification map for the follow-up scan. This probability is defined as the product of all the transition values (taken from the tumor transition model, P) of the classified voxels from C_B (the baseline classification map) to C_m

$$p\left(C_m\right|C_B,P(·))=\prod _{k=1}^{N_t}P(C_B\left(k\right),C_m\left(k\right)),$$ (5)

where k denotes a spatial index and N_t denotes the number of voxels labeled as tumor in the baseline scan. All possible combinations of the components were listed and one which maximized Eq. 5 was selected as the classification map of the follow-up scan.

The result is an internal classification map of the tumor in the follow-up scan in the region of the baseline tumor area, denoted as C and coined hereinafter partial classification map. This map yields the statistical distribution of each tumor component in the follow-up scan. It is used to update the evolving boundaries, as described in Sec. 2D.

Step 4: Tumor boundaries update

In this step, the changing boundaries, found in step 2, are updated using the information about each tumor component which was extracted in step 3. For every component, we define the similarity map D_q that represents the similarity of each voxel in the follow-up scan to component q, using the previously computed statistical distribution parameters of this component, as Mahalanobis distance

$$D_q\left(i\right)={({\tilde{V}}_F\left(i\right)-\widehat{{\mu }_q})}^T{\widehat{C}}_q^{-1}({\tilde{V}}_F\left(i\right)-\widehat{{\mu }_q}),$$

where q = 1…N_C is the component index and i is a spatial index. In other words, the smaller the value of D_q(i), the more similar the voxel i to component q. The parameters $\widehat{{\mu }_q}$ and $\widehat{C_q}$ are the sample mean and covariance of the follow-up scan voxels labeled with the component q in the partial classification map, C. In this manner, the estimated mean vector and covariance matrix of the follow-up scan are computed from the follow-up scan itself, obviating the need for gray-level normalization for this purpose.

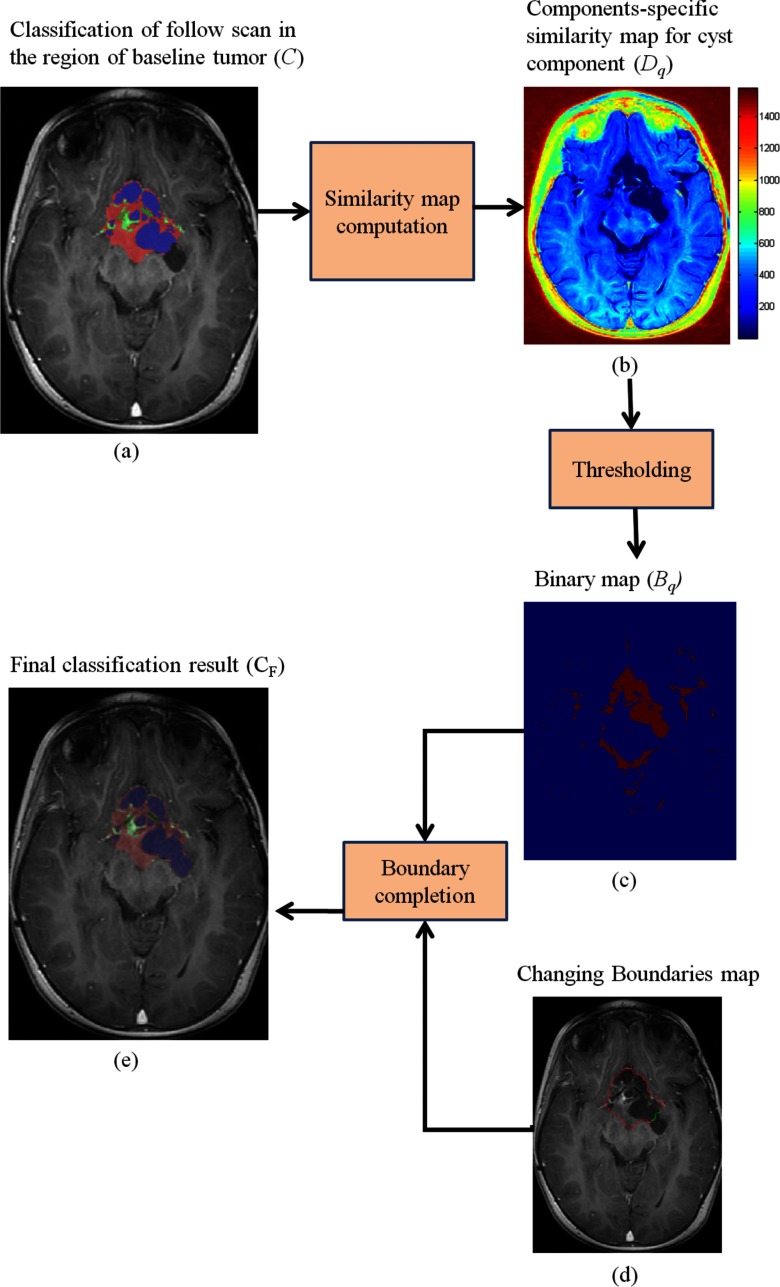
Next, we threshold the similarity map, D_q, with the average value of its voxels that are labeled as component q in the partial classification map C. The result is N_C binary maps, denoted as ${\left\{B_q\right\}}_{q=1}^{N_C}$. Then, for every changed boundary segment (found in step 2), we select the binary map, B_q, that corresponds to component adjacent to the changed boundary segment in the classified follow-up scan. We update the tumor boundary by tracing the boundary of the binary map, from the start of the changing boundary segment toward its end, where unclassified voxels are classified to one of the tumor components with MAP estimator based on the statistical parameters which were computed in step 3. The result is an updated segmentation of the tumor, and a delineation of the components, C_F, which is consistent with the baseline scan. Figure 7 shows a flow chart describing the process of how the tumor boundary is updated, together with an example of the final classification map, C_F.

Figure 7.

A flow chart showing details of the tumor boundaries update process. The classification map C in (a) is the result of the tumor growth modeling process described in step 3; (b) we compute the similarity map, D_q for each component, where the similarity map of the cyst components is shown in (a); (c) we threshold D_q to obtain a binary map, B_q for each component; (d) we use B_q in conjunction with the changing boundary map resulted from step 2 to obtain the final classification result (e), after a boundary completion process.

Data acquisition

We conducted a retrospective evaluation experiments of our method with clinical multisequence MR datasets. We chose patients with different types of LGTs, OPG, and thalamic astrocytomas, whose MR scans were acquired at separate institutions, to emphasize the robustness of the method. Table 1 shows the details of the patients and the scans. Each scan consists of postcontrast T1-weighted (T1c) and T2-weighted (T2W) images. Both sequences were acquired with spin echo (SE) sequence, flip angle = 90°, while TR/TE values varied between 340/6.9 and 540/15 ms for the T1c imaging contrast, and between 3120/80 and 4700/142 ms for the T2W imaging contrast.

Table 1.

Summary of experimental data.

		Patients age	Number of	Number of	Data dimensions	Voxel size
Tumor type	Institution1	(years)	patients	scans	(voxels)	(mm × mm × mm)	MRI type
OPG	TASMC	4–14	5	25	512 × 512 × 30	0.5 × 0.5 × 5.0	GE Signa 1.5T HDXT
Thalamic astrocytomas	LPCH	4–11	5	25	408 × 512 × 24	0.45 × 0.45 × 6.25	GE Signa 3T HDXT

¹TASMC = Tel Aviv Sourasky Medical Center, LPCH = Lucile Packard Children's Hospital at Stanford.

Thalamic astrocytomas patients were scanned every three months and OPG patients were scanned every five months to generate five scans per patient (total of 50 scans). The first scan of each patient was used as the baseline scan and the remaining scans were used to evaluation. As a result, 40 scans were used to evaluate the method's performance.

One radiologist from each institution manually produced segmentations for the scans acquired at his/her institution using Analyze Direct 10 (Mayo Clinic, Rochester, MN). These segmentations are considered as the gold standard. The tumors consist of three different internal components: solid, enhancing, and cyst, therefore, N_C = 3.

EXPERIMENTAL RESULTS

Data evaluation

Three means of evaluation were used to quantify the performance of our method vs the gold standard. The first two measures quantify the performance of the method in terms of segmenting the gross total volume of the tumor. The third measure quantifies the ability of the method to reliably track the evolution of tumor components over time:

• 1.
  Gross total volume based measures: We measured the volumetric similarity of the gross total volumes, also known as the Dice similarity measure defined as

  $$\text{Dice}=\left(\frac{2\times |S\bigcap R|}{\left|S\right|+\left|R\right|}\right)\times 100,$$

  where S and R refer to the method result and the gold standard, respectively. In addition, we measured the absolute volume difference (AVD) between the method's result and the gold standard, defined as

  $$\text{AVD}=100\times \left|\frac{S}{R}-1\right|.$$ (6)
• 2.Gross total volume surface based measures: We measured the distance between the surfaces of the tumor volumes provided by our method and by the gold standard. For this purpose, we used the mean surface distance (MSD) and the Hausdorff distance.^{42, 43}
• 3.Longitudinal correlation of tumors components: We defined a component difference vector, which consists of the differences in volume of a tumor component between every two consecutive time points. The difference vector represents the changes of tumor component over the time, per patient. We then compute difference vectors for every tumor component over time, for each patient. These vectors are computed twice: once with the gold standard data and once with the method's results data. Then, the Pearson correlation coefficients between the matching gold standard and the method results' difference vectors are computed.⁴⁴ This measure quantifies the ability of the method to reliably track longitudinal changes in the internal tumor components of the tumor.

The training and evaluation of the method is carried out using the leave-one-out cross-validation method. For each group of patients with the same tumor type, the scans of four patients are used for training. The remaining patient's scans are used to validate the method and are tested with the parameters extracted in the training procedure. This process is repeated five times, each time a different patient is used for validation experiment. Overall, the results are validated using a total number of ten patients, five from each group, in a “patient-independent” mode.

First, we describe the training procedure to estimate the components transition matrix P(t) and the four adjustable parameters of the algorithm, K, r_T, γ, and α. Then, we describe the evaluation results of the experiments.

Training procedure

In our experiments, we use the extended components transitions model appears in the Appendix. Therefore, the training procedure consists of the estimation of the components transition matrix P(t) for each tumor type. In addition, four parameters are estimated: the number of voxels per boundary segment, K, the radius of the tumor boundary surrounding area, r_T, the Davies Bouldin index threshold, γ, and the proportion coefficient, α. These parameters are determined as follows.

First, we register the follow-up scans of the patients used for training to their baseline ones. Then, we estimate the components transition matrix P(t) as described in the Appendix, using the manual segmentation maps of the patients used for training.

Then, we use the gradient descent algorithm⁴⁵ to estimate the value of the four adjustable parameters, as follows. We use the baseline delineations of each patient used for training to segment his/her follow-up scans with the method described in this paper, where each follow-up segmentation serves as the prior segmentation to its consecutive scan. We use a set of fixed parameters and P(t) as computed above. We set the initial fixed parameters based on our datasets' spatial dimensions and the nature of LGTs to: K = 5, r_T = 5, γ = 0.13, and α = 0.6. We then compute the Dice similarity measure for each segmentation result and use the average Dice value over the segmentation as the cost function to optimize for the gradient descent algorithm, to update the set of parameters. We repeat this process for all parameters until convergence.

Validation results

We used the patients' first scan and its delineation as the baseline scan, and evaluated our method with the four follow-up scans. In total, 40 scans (20 for each tumor type) were used to evaluate the method.

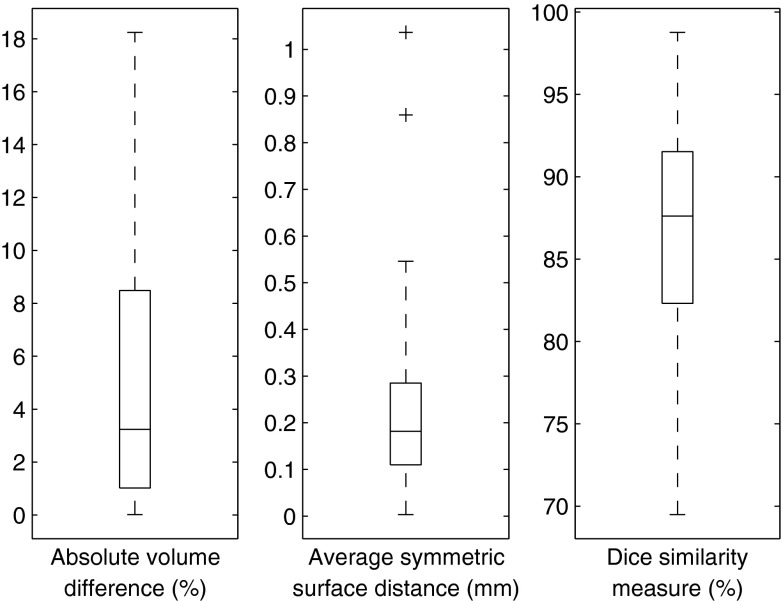
Gross total volume results

A summary of the gross total volume results is presented in Table 2. Figure 8 shows the distribution of the results as compared to the gold standard. Figure 9 shows an illustrative example of the results vs the gold standard, where the internal components of the tumor are also delineated.

Table 2.

Summary of gross total volume experimental results.

	Dice	AVD	MSD	Hausdorff
Tumor type	measure (%)	(%)	(mm)	distance (mm)
OPG	88.46	5.11	0.24	8.06
Thalamic astrocytomas	84.7	5.13	0.25	17.61
Average	86.58	5.12	0.25	12.84

Figure 8.

Segmentation results for 40 cases. The central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the extreme data points. Outliers are plotted individually as “+.”

Figure 9.

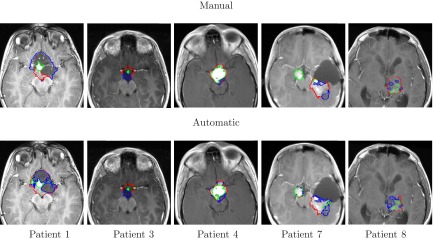
Segmentation and internal classification of LGT. Representative results for OPG (patients# 1, 3, 4) and thalamic astrocytomas (patients# 7, 8) overlaid on T1c image: manual (top) vs automatic (bottom). Solid, enhancing and cystic areas are presented.

Tumor components longitudinal tracking results

Figures 1011 show the longitudinal changes of OPG and thalamic astrocytomas components' volumes obtained using the proposed method as compared to the gold standard. Note that the proposed method results and the gold standard show the same disease progression. For example, for patient 1, both the method results and the gold standard exhibit a steady tumor volume during the first 20 months, with an increase of the cystic component after 23 months. Patient 7 is another example, where both the automatic results and the gold standard show a gradual increase in the cyst component and in the gross total volume between months 3 and 13.

Figure 10.

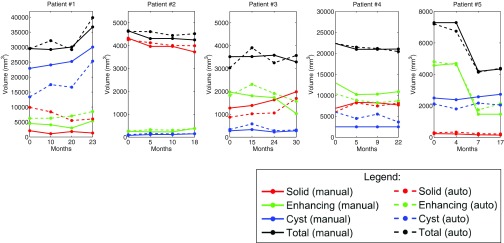
OPG progression of patients 1–5. Gold standard and method results for each patient are presented. The baseline scan is not included.

Figure 11.

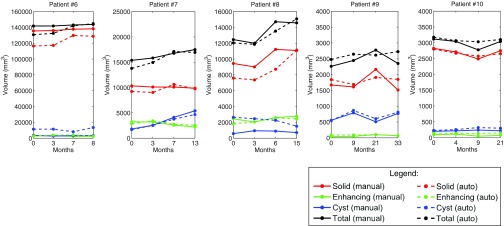
Thalamic astrocytomas progression of patients 6–10. Gold standard and method results for each patient are presented. The baseline scan is not included.

We used the longitudinal correlation measure, described above, to quantify the ability of our method to track the evolution of tumor components over time. Note that since our method is tested on four time points for each patient, we compute a difference vector of length three, per component, per patient. Table 3 shows the Pearson correlation coefficients for each component over time, per patient.

Table 3.

Pearson correlation coefficients between method's and gold standard's difference vectors of components volumes over time. The high correlation values (>0.5 in most cases) indicate high correlation between the method's results and the gold-standard, in terms of tumor components progression estimation.

OPG patients
	Patient #
Component	1	2	3	4	5
Solid	−0.61	−0.11	0.72	0.74	0.87
Enhancing	0.79	0.49	0.34	0.92	0.98
Cystic	0.85	0.93	0.93	0.99	0.78
Thalamic astrocytomas patients
	Patient #
Component	6	7	8	9	10
Solid	0.98	0.95	0.21	0.74	0.93
Enhancing	0.06	0.99	0.33	0.95	0.38
Cystic	0.16	0.84	0.73	0.97	0.96

The correlation results indicate the reliability of our method in estimating the growth trend of each component over time. Note that Table 3 includes some small or negative correlation coefficients values. A closer look at the table and at Figs. 1011 reveals that low correlation values are mostly found in cases where the temporal changes in the tumor components volume are small. In such cases, minor mismatches between the gold standard and the method's results may result with low correlation values, although both of them indicate a steady tumor component volume over time, in clinical terms. For example, a negative correlation value is obtained for the solid component of patient #2. A closer look at the temporal change of this component in Fig. 10 reveals that both our method and the gold standard indicate a steady solid tumor volume over time, in clinical terms. However, the minor opposite volume change trends over time caused a negative correlation value for these components.

Overall, the method exhibits slightly better results for OPG than for thalamic astrocytomas. We believe that the tumor type is the main cause for this phenomenon. OPGs are usually smaller and more stable over time than thalamic astrocytomas, making it easier for the automatic method to track longitudinal changes.

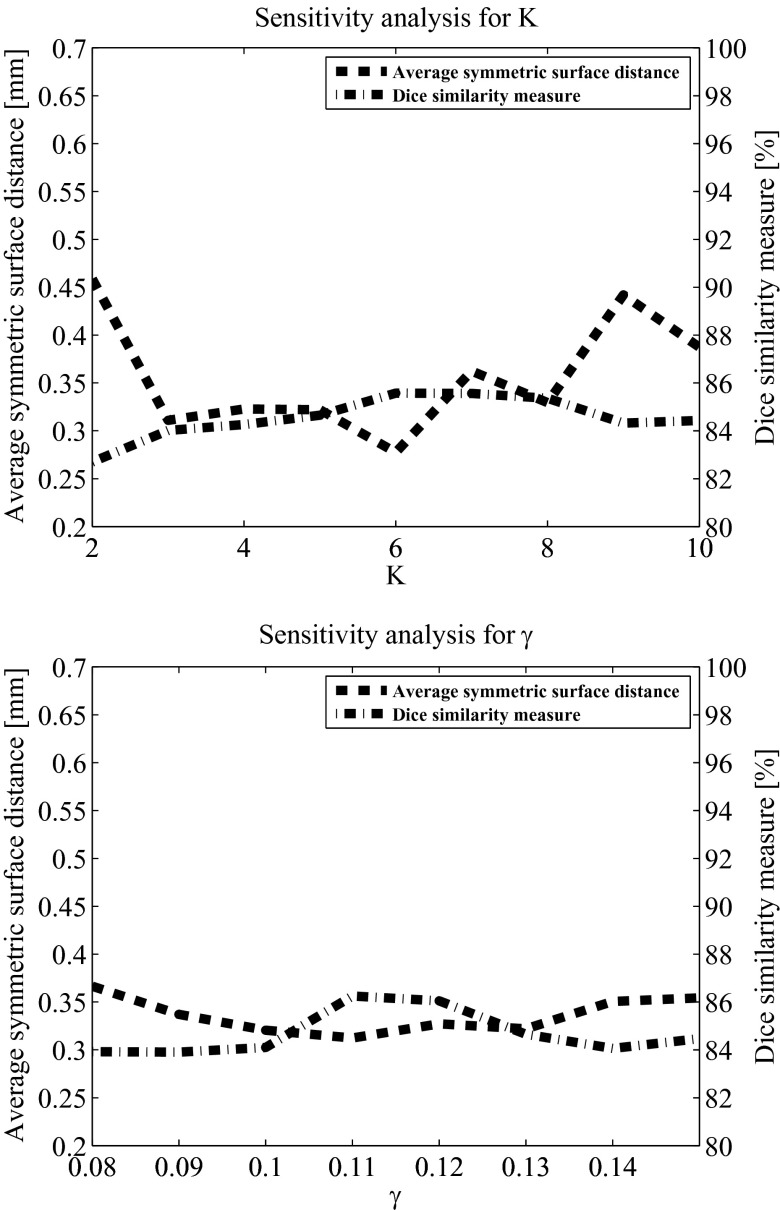
Parameter sensitivity analysis

The method includes four adjustable parameters: the number of voxels per boundary segment, K, the radius of the tumor boundary surrounding area, r_T, the Davies Bouldin index threshold, γ, and the proportion coefficient, α. The value of these parameters is determined in the training procedure described above. We study the sensitivity of our method to those parameters to understand its performance with suboptimal parameters selection. We computed the average values of the Dice similarity measure and the average symmetric surface distance based on various parameters values over 40 scans. In our analysis, three parameters were fixed while the sensitivity to the fourth was examined. For consistency, the fixed parameters values in this analysis are the ones that were used as the initial values for the gradient descent algorithm in the training phase.

In our analysis, the Dice measure in all cases was above 80%. Figure 12 presents the parameter sensitivity analysis results for K and γ. Although the method's performance varies with respect to selection of its parameters, it exhibits reliable performance even in cases where the parameters were not optimized.

Figure 12.

Parameter sensitivity analysis results of K and γ. In each analysis, three parameters remained fixed while the fourth varied. The fixed values were: number of voxels per boundary segment, K = 5; radius of the tumor boundary surrounding area, r_T = 5; Davies Bouldin index threshold, γ = 0.13; and proportion coefficient, α = 0.6.

DISCUSSION

Comparison with other tumor segmentation methods

Most of the published literature on brain tumor segmentation deals with GBM. Therefore, it is difficult to provide an accuracy value of reference of state-of-the-art LGT segmentation methods. Note that state-of-the-art GBM segmentation methods^{9, 11} reported a 30% volumetric overlap error, which is equivalent to Dice similarity measure of 70%.

In this section, we compare the gross total volume results of our method to those of our previously published method for OPG segmentation³³ on the OPG datasets presented in this paper, and to a simple segmentation method that propagates the baseline segmentation as is, over time. The mean Dice similarity measure between the volumetric results of our previously published method³³ as compared to manual segmentation by an expert radiologist is 70.44%, and the mean surface distance is 0.6 mm. It can clearly be seen that our current method outperforms our previous one, thanks to the strong prior of the baseline segmentation and the spatiotemporal model.

To evaluate the role of a baseline segmentation as prior knowledge, we applied a simple method that directly propagates the baseline segmentation, with no boundary update. This method was tested on both the OPG and the thalamic astrocytomas datasets presented in this paper. The mean Dice similarity measure between the volumetric results of this experiment as compared to manual segmentation by an expert radiologist is 76.24%, and the mean surface distance is 0.6 mm. This comparison shows that a baseline segmentation as a prior knowledge for the segmentation of the follow-up scan improves the results by approximately 7%, if we compare it to our previously published method. The additional improvement of 9% presented in this paper, yielding a Dice similarity measure of 86.58%, is due to the spatiotemporal model and the boundary update process.

Comparison with general segmentation algorithms

Based on our experience with all-purpose clinical segmentation softwares (e.g., Analyze), our method is much more efficient, in terms of segmentation time. General purpose segmentation algorithms do not take into account prior knowledge about the patient and the tumor involved, and therefore they are somewhat “blind” to the tumor's specific characteristics. They require manual parameters selection on a case by case basis. The fact that our method uses the baseline scan and requires the baseline scan segmentation for the follow-up scan segmentation, allows it to be much more tailored toward the follow-up scan at hand.

One of the major advantages of the method is the time it requires for segmentation. While general purpose segmentation methods require user interactive segmentation process which may last up to 30 min, our method provides the segmentation result in about 5 min of computation time with no user interaction.

Relation to prior research

Our method consists of four steps, some of which incorporate and extend previously published methods. Incorporating information from multiple scans of the same patient to segmenting a MR scan was previously proposed.^{10, 24, 27, 28, 29} We extend the idea of incorporating information from other scans to include: (1) the internal classification of the tumor over time, and (2) the development of a semiautomatic and repeatable method for tumor follow-up.

Modeling tumor intensity values with a Gaussian mixture model is a common approach.^{9, 11} Markov models are also widely used in MR image analysis.^{46, 47, 48} However, to the best of our knowledge, modeling of changes in tumor components over time as a spatiotemporal model is novel for LGT.

Baseline segmentation

Our method requires an initial segmentation of the baseline scan. Baseline segmentation has been previously addressed.^{3, 9, 10, 11, 13, 14, 18, 24, 35, 49} This segmentation can be obtained manually, semiautomatically, or automatically in specific cases.^{9, 33}

The initial segmentation serves as strong prior information for the tumor components boundaries. It increases the replicability of the method and, with the statistical model developed in the paper, obviates the need for the gray-level normalization since the components gray-level range is estimated from the follow-up scan itself. Therefore, we believe that the initial segmentation of the baseline scan is worth the effort, especially in cases where state-of-the-art automatic or semiautomatic brain tumor segmentation methods can be used to reduce the manual segmentation time.

An additional issue related to the baseline segmentation is the sensitivity of the method to the baseline segmentation. Since the follow-up segmentation relies on the baseline segmentation, the method is actually “biased” toward the expert that segmented the baseline scan. Based on our experience with the method, this phenomenon also occurs in cases where the baseline scan was automatically segmented. However, this bias is mostly relevant in fuzzy boundaries of the tumor, as sharp boundaries are usually agreed upon. Additionally, since in most cases only the change in the tumor volume over time is the important factor for treatment decision, this bias is balanced out when we examine the tumor growth trend over time.

Error propagation

The propagation of information from the baseline to subsequent time points may cause a build-up of errors for the later time points. To better understand this phenomenon, we analyzed the Dice similarity measure for all patients over time. We obtained that mean Dice similarity varies between 89.57% for the first time point and 85.65% for the fourth time point. This error build-up trend, however, could be meaningful where more time points per patient are involved.

A possible solution would be to provide an additional manual annotation to one of the later time points as well, and to use a forward-backward mechanism to propagate the information between time points. While out of the scope of this paper, we refer the reader to methods for forward-backward segmentation mechanism in MR images.^{21, 50} Examples for similar methods in brain MRI longitudinal analysis can be found in the works of Reuter et al.^{29, 51}

Tumor regression

Healthy areas and tumor components mostly have different gray-levels in the MR scan. Therefore, healthy areas are expected to have high values in the tumor component similarity maps, D_q, defined in step 4. As a result, healthy voxels will not be included in the binary maps, B_q, and will not be part of the tumor delineation. When a significant tumor regression is expected, it is possible to explicitly add a healthy or nontumor component to the transition model and then estimate the transition probabilities from the tumor components and the healthy component.

CONCLUSIONS

We have presented a new method for the segmentation and classification of LGT brain tumors from MRI follow-up scans. Our experimental results indicate that our method accurately segments and classifies OPG and thalamic astrocytomas in the follow-up scheme. The main contributions of this paper are:

Follow-up of tumor components

Currently, manual delineation is used as the gold standard for volumetric quantification of brain tumors and their components. Due to inter/intraobserver variability, this delineation has intrinsic uncertainty and possible bias. Since therapeutic decision making relies heavily on tumor volume and internal changes over time, repeatable delineation of the tumor plays an important role in the decision process.

A novel aspect of this method is its ability to track the evolution of internal tumor internal components and not just the gross total volume of the tumor. The accurate evaluation of the changes in tumor components over time sheds light on the response to various therapies and the natural history of the tumors. To the best of our knowledge, no other method for the segmentation of internal components of brain tumor was validated longitudinally.

No need for gray-level normalization

In many image processing tasks, previously learned gray-level intensity models are used to segment or classify various patterns. Gray-level intensity normalization is mostly necessary in those cases. This normalization procedure might be error prone and does not always overcome the inherent gray-level variability. Our method bypasses the issue by deriving the statistical gray-level model from the input follow-up scan itself. As a result, a gary-level intensities model for the tumor components is uniquely developed for each follow-up scan, which makes our method potentially robust for multicenter studies, where multiple scanners are used.

Clinical significance

The potential clinical significance of LGT segmentations is to save time and effort to the radiologist and to provide an automatic tool to reliably determine the tumor boundary and to delineate the tumor components. The method was developed and tested to match the common scheme for tumor treatment evaluation, which is based on study of longitudinal tumor growth.

Reliable tracking tumor's internal tumor components evolution is essential for treatment evaluation. The repeatable delineation of the tumor boundaries and the tracking of tumor components evolution over time is expected to increase the confidence level of the clinical staff in the volumetric measurements and to help with identifying early response to treatment.

Future work will include expanding the experimental results of this work to segment and classify other types of brain tumors, including low and intermediate grade tumors.

APPENDIX: EXTENSION OF THE TRANSITION MODEL TO SUPPORT DEPENDENCY ON TIME BETWEEN SCANS

In this appendix, we extend the tumor components transition model, presented in Sec. 2C. In many cases, such as the cases presented in our experiments, longitudinal scans are performed with uneven time gaps between time points. This fact necessitates the extension of the simplified transition model to support dependency on time between scans, as follows.

If we assume that the transition model depends in the time between the baseline and the follow-up scans, the transition probability matrix is defined as $P\left(t\right)={\left\{p_{ij}\left(t\right)\right\}}_{i,j=1}^{N_C}$. To estimate its elements from a set of patients used for training each with several scans acquired over time, we assume that we have the manually delineated tumor components classification maps for each scan. These classification maps are used to estimate the elements of P(t) as follows.

Let N_E denote the number of patients used for training. Let N_Sk denote the number of scans of the kth patient used for training (N_Sk > 1), acquired at time points: $T_k=t_{0k},t_{1k},...,t_{N_{Sk}}$, and $C_k=C_{0k},C{t}_{1k},...,C_{N_{Sk}}$ denote its corresponding manually delineated tumor components classification maps. Based on two maps from two different time points, t_nk and t_mk (n > m) we estimate ${\widehat{p}}_{ij}^k\left(t_{mn}\right)$, which is the estimation of p_ij(t_mn) for time point t_mn = t_nk − t_mk, based on the kth patient solely. This value is estimated as the proportion of the transitions from component i to component j between the classification maps of these time points. The formula is

$${\widehat{p}}_{ij}^k\left(t_{mn}\right)=\frac{1}{N_v}\sum _{l=1}^{N_v}\delta (C_{nk}\left(l\right),j)\delta (C_{mk}\left(l\right),i),$$ (A1)

where δ(·) is the Kronecker delta function

$$\delta (x-a)=\left\{\begin{array}{cc}1\hfill & \text{if}x=a\hfill \\ 0\hfill & \text{if}\text{otherwise}\hfill \end{array}.\right.$$ (A2)

The parameter N_v is the number of voxels segmented as tumor in C_mk, and l is an index representing spatial location in C_mk and C_nk.

Repeating this procedure for every pair of time points from T_k results in an estimation of the transition matrix based on the kth patient, for discrete time points, which is then interpolated to match a required time scale. To obtain an estimation from all the patients, this process is repeated for every patient, resulting in: ${\left\{{\widehat{p}}_{ij}^k\left(t\right)\right\}}_{k=1}^{N_E}$. Under the assumption that patient's classification maps are independent, we average the results over all the patients used for training to obtain the final estimation of the transition matrix

$${\widehat{p}}_{ij}\left(t\right)=\frac{1}{N_E}\sum _{k=1}^{N_E}{\widehat{p}}_{ij}^k\left(t\right).$$ (A3)