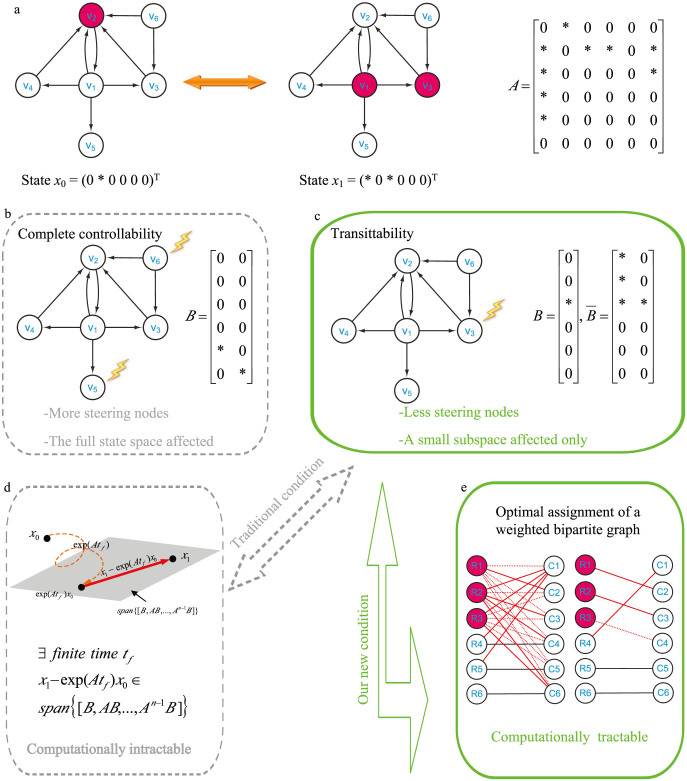
Figure 1. Illustration of network transittability.

(a) Considering the transittability of the network between two specific states x₀ and x₁ as shown here and finding the steering kernel for such a state transition. Nodes with the same color at two states (e.g., v₄, v_5, v₆) indicates that they are unchanged while nodes with different colors (e.g., v₂, v₁, v₃) indicates that they are unchanged at two states. “*” in the structure matrix A of the network represents the free parameters while “0” represents the fixed parameters. “*” in two states x₀ and x₁ represents the value of corresponding nodes different while “0” represents the value of corresponding nodes indifferent at two states. (b) From the concept of complete controllability, two input control signals should be directly applied to two steering nodes v₆ and v₅ to transit the network between any two states, including two specific states x₀ and x₁. One can see that (1) more steering nodes than necessary are needed and (2) the full state space with six dimensions is affected for such a state transition, which may cause side effects. (c) From our new concept of transittability and new theorems, only one steering node v₃ is needed for the transition between two specific states x₀ and x₁. (d) This is the traditional sufficient and necessary condition for transittability of two specific states x₀ and x₁ which is actually intractable. (e) Using our new sufficient and necessary condition for transittability of two specific states x₀ and x₁, we can identify the steering kernel by solving an optimal assignment of weighted bipartite graphs via an efficient graph-theoretic algorithm.